Skip to main content
LibreTexts - Ukrayinska

5.3: Вправи

  1. Last updated
  2. Save as PDF
  • Page ID
    34983

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Вправа\(\PageIndex{1}\) Pitot tube

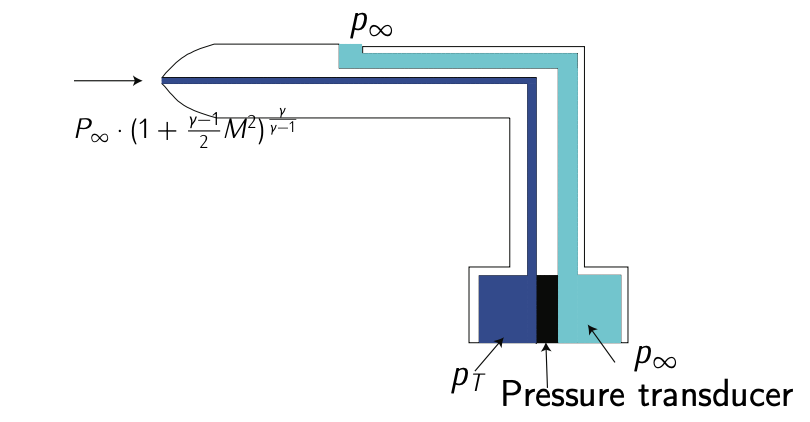
    2022-01-20 8.30.26 пнг
    Малюнок 5.19L трубка Піто.

    Літаки використовують трубки Піто для вимірювання швидкості повітря. Вони складаються з трубки, спрямованої безпосередньо в потік рідини, такої, що рухається рідина доводиться в спокій (застій тиску повітря,\(p_T\)). Як правило, труби піто включають також статичний порт для вимірювання статичного тиску повітря (\(p_{\infty}\)). Див. Рис. 5.19 як ілюстрацію, розглядаючи повітря як стисливий потік.

    Розглянемо наступні вимірювання на борту літака:

    • Трубка Піто вимірює тиск застою\(p_T = 36975\ Pa\).
    • Статична частина вимірює статичний тиск\(p_{\infty} = 22500\ Pa\).

    Припустимо також, що:

    • повітря можна вважати ідеальним газом.
    • повітря слід вважати стисливою рідиною. Для стисливого потоку, один має, що

    \[P_T = P_{\infty} \cdot \left (1 + \dfrac{\gamma - 1}{2} M^2 \right )^{\tfrac{\gamma}{\gamma - 1}},\]

    з\(\gamma = 1.4\) адіабатичним коефіцієнтом повітря, і\(M\) числом Маха:

    \[M = \sqrt{V_{TAS}}{\sqrt{\gamma RT}}\]

    Розрахуйте калібровану швидкість повітряного судна (CAS). 8

    Відповідь

    Зверніть увагу, що можна застосувати рівняння Бернуллі до лінії потоку рідини в трубці Піто. Припускаючи стисливий потік, один має:

    \[P_T = P_{\infty} \cdot \left (1 + \dfrac{\gamma - 1}{2} M^2 \right )^{\tfrac{\gamma}{\gamma - 1}}.\]

    Припускаючи також, що повітря можна вважати ідеальним газом, один має:

    \[P = \rho \cdot R \cdot T.\]

    Крім того, один має таке відношення:

    \[M = \dfrac{V_{TAS}}{\sqrt{\gamma RT}}.\]

    Загалом, розробляючи з цими трьома рівняннями, один має:

    \[P_T = P_{\infty} \cdot \left (1 + \dfrac{\gamma - 1}{2} \dfrac{\rho_{\infty} \cdot V_{TAS}^2}{\gamma \cdot P_{\infty}} \right )^{\tfrac{\gamma}{\gamma - 1}}.\]

    Розглядаючи\(P_T - P_{\infty} = \Delta P\) та ізолюючи\(V_{TAS}^2\):

    \[V_{TAS}^2 = \dfrac{2\gamma}{\gamma - 1} \cdot \dfrac{P_{\infty}}{\rho_{\infty}} \left (\left (\dfrac{\Delta P}{P_{\infty}} + 1 \right )^{\tfrac{\gamma - 1}{\gamma}} - 1 \right ).\]

    Однак слід зауважити, що тільки з трубкою Піто і статичним портом не можна виміряти ні температуру, ні щільність. Таким чином,\(V_{TAS}\) неможливо безпосередньо розрахувати (нам знадобляться додаткові прилади/датчики). Це є причиною концепції Calibrated Airspeed (CAS): справжня швидкість польоту літака буде мати, якщо літати зі стандартними середніми умовами рівня моря. Таким чином, CAS визначається наступним чином:

    \[V_{CAS}^2 = \dfrac{2\gamma}{\gamma - 1} \cdot \dfrac{P_{MSL}}{\rho_{MSL}} \left (\left (\dfrac{\Delta P}{P_{MSL}} + 1 \right )^{\tfrac{\gamma - 1}{\gamma}} - 1 \right ).\label{eq5.3.8}\]

    Дійсно, швидкість польоту, яка відображається в кабіні пілоту (іменована як Indicated Airspeed) - це швидкість CAS, виправлена помилками приладу.

    Тепер, вводячи в Eq. (\(\ref{eq5.3.8}\)) зі значеннями, наведеними в твердженні, один має рішення задачі:

    \[V_{CAS} = 150\ m/s.\nonumber\]

    8. припустимо, що середні умови рівня моря є стандартними відповідно до ISA,\(P_{MSL} = 101325\ Pa\) і\(\rho_{MSL} = 1.225\ kg/m^3\)