Skip to main content
LibreTexts - Ukrayinska

4.1: Загальні положення

  1. Last updated
  2. Save as PDF
  • Page ID
    34965

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

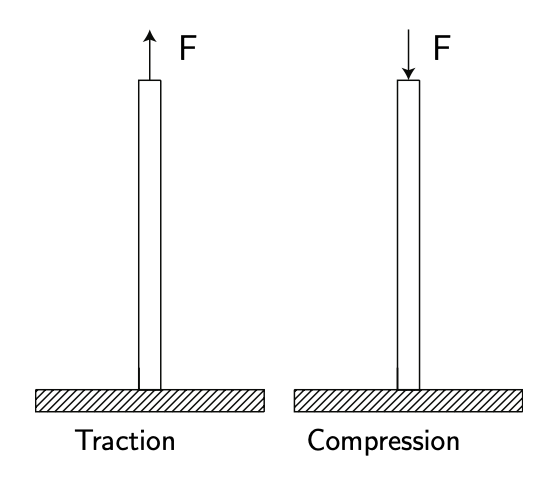
    2022-01-19 пнг
    Малюнок 4.1: Нормальне напруження. Адаптовано з\(F_{\text{RANCHINI}}\) та ін. [2].

    Завданням конструктора є врахування всіх можливих навантажень. Поєднання матеріалів і конструкція конструкції повинна бути такою, щоб вона могла витримувати навантаження без відмов. Для оцінки таких навантажень можна проводити вимірювання під час польоту, проводити вимірювання масштабної моделі в аеродинамічній трубі, робити аеродинамічні розрахунки та/або виконати тестові польоти з прототипом. Конструкції літаків повинні бути здатні витримувати всі умови польоту і вміти працювати при будь-яких умовах корисного навантаження.

    Сила, прикладена вздовж до шматка структури, призведе до нормального напруження, будучи або напругою (також називається тягою) або напругою стиснення. Див. Малюнок 4.1. При навантаженнях на розрив все, що має значення, - це площа, яка знаходиться під напругою. При стискаючих навантаженнях також важлива форма, так як може виникнути вигин. Напруга визначається як навантаження на площу, буття\(\sigma = F/A\).

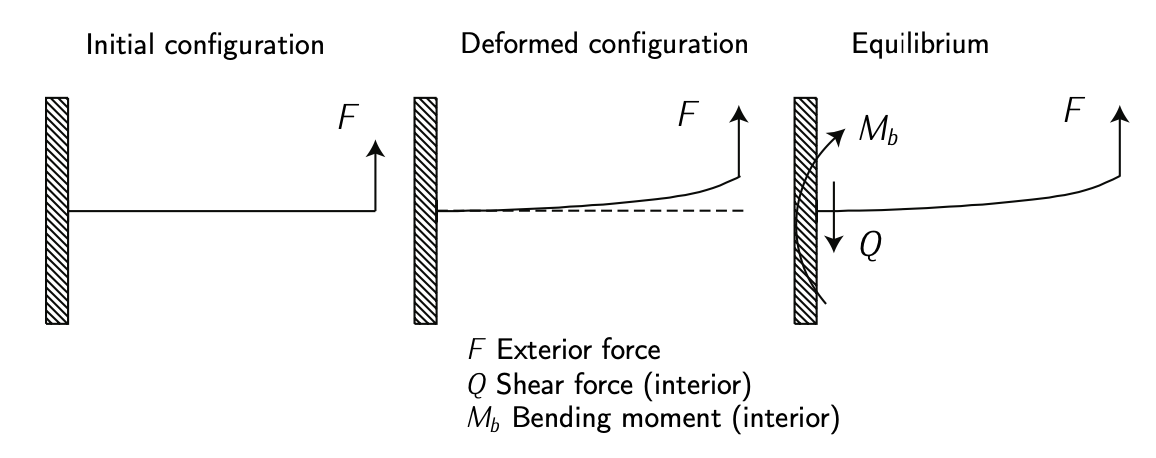
    2022-01-19 8.53.51 PNG
    Малюнок 4.2: Вигин. Адаптовано з\(F_{\text{RANCHINI}}\) та ін. [2].

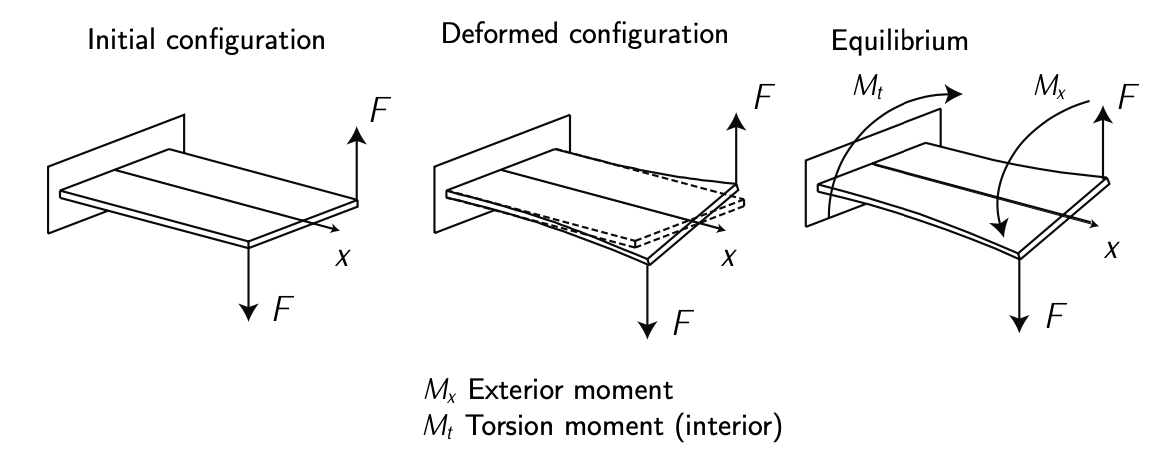
    2022-01-19 пнг
    Малюнок 4.3: Кручення. Адаптовано з\(F_{\text{RANCHINI}}\) та ін. [2].

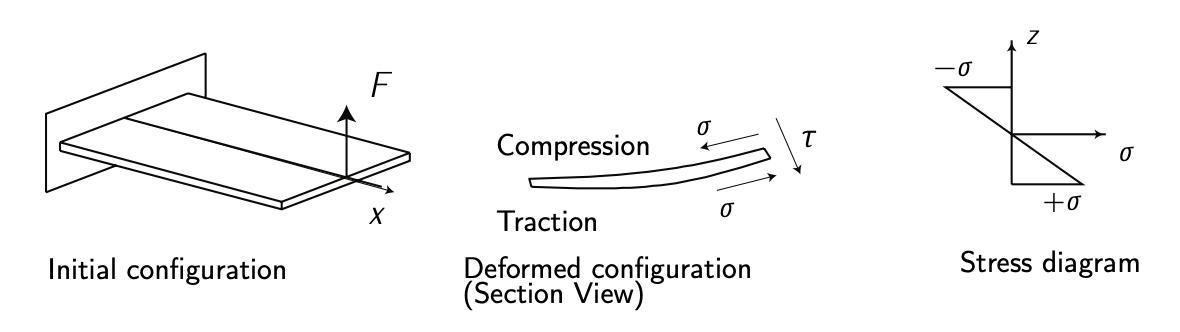
    2022-01-19 пнг
    Малюнок 4.4: Напруження зсуву внаслідок вигину. Адаптовано з\(F_{\text{RANCHINI}}\) та ін. [2].

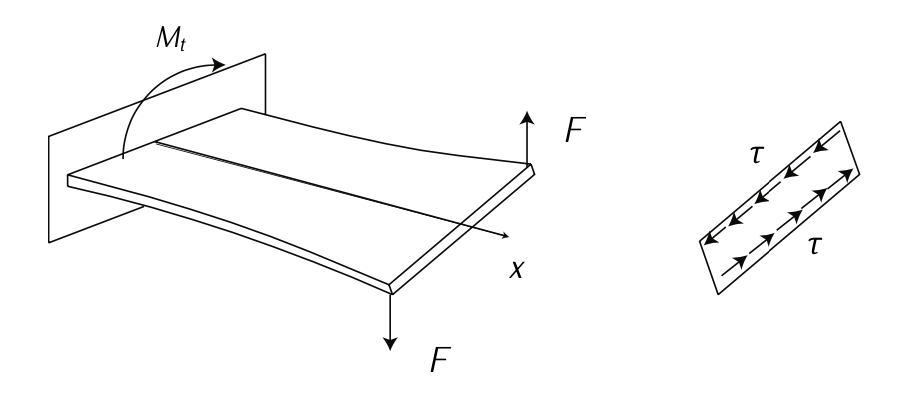
    2022-01-19 см 8,56.57 PNG
    Малюнок 4.5: Напруження зсуву внаслідок кручення. Адаптовано з\(F_{\text{RANCHINI}}\) та ін. [2].

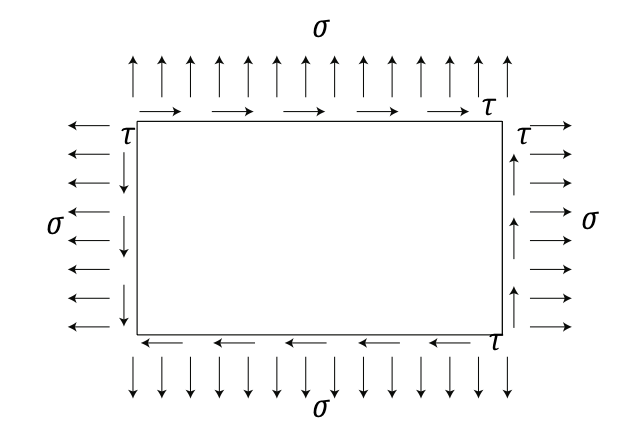
    2022-01-19 пнг
    Малюнок 4.6: Напруження в пластині. Адаптовано з\(F_{\text{RANCHINI}}\) та ін. [2].

    Якщо сила прикладена під прямим кутом (скажімо, перпендикулярно до довжини балки), вона застосовуватиме напругу зсуву та згинальний момент. Див. Рисунок 4.2. Якщо сила зміщена від лінії балки, це також спричинить кручення. Див. Малюнок 4.3. Як вигин, так і кручення викликає напруження зсуву. Зсув - це форма навантаження, яка намагається розірвати матеріал, змушуючи атоми або молекули ковзати один над одним. Див. Малюнок 4.4 і рисунок 4.5. Загалом, прототипова структура страждає як від нормальних (\(\sigma\)), так і зсувних (\(\tau\)) напружень. Див. Рис. 4.6, на якому показаний наочний приклад напружень над пластиною.

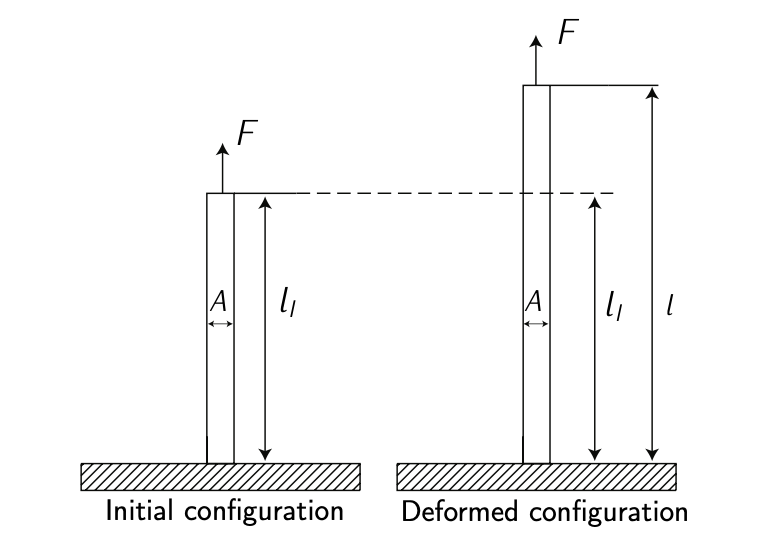
    2022-01-19 пнг
    Малюнок 4.7: Нормальна деформація. Адаптовано з\(F_{\text{RANCHINI}}\) та ін. [2].

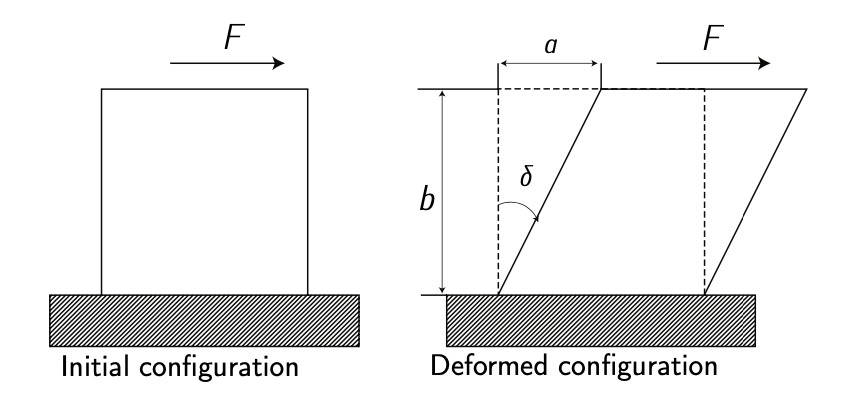
    2022-01-19 пнг
    Малюнок 4.8: Тангенціальна деформація. Адаптовано з\(F_{\text{RANCHINI}}\) та ін. [2].

    Конструкції, схильні до нормальних або зсувних напружень, також можуть деформуватися. Див. Малюнок 4.7 і рисунок 4.8.

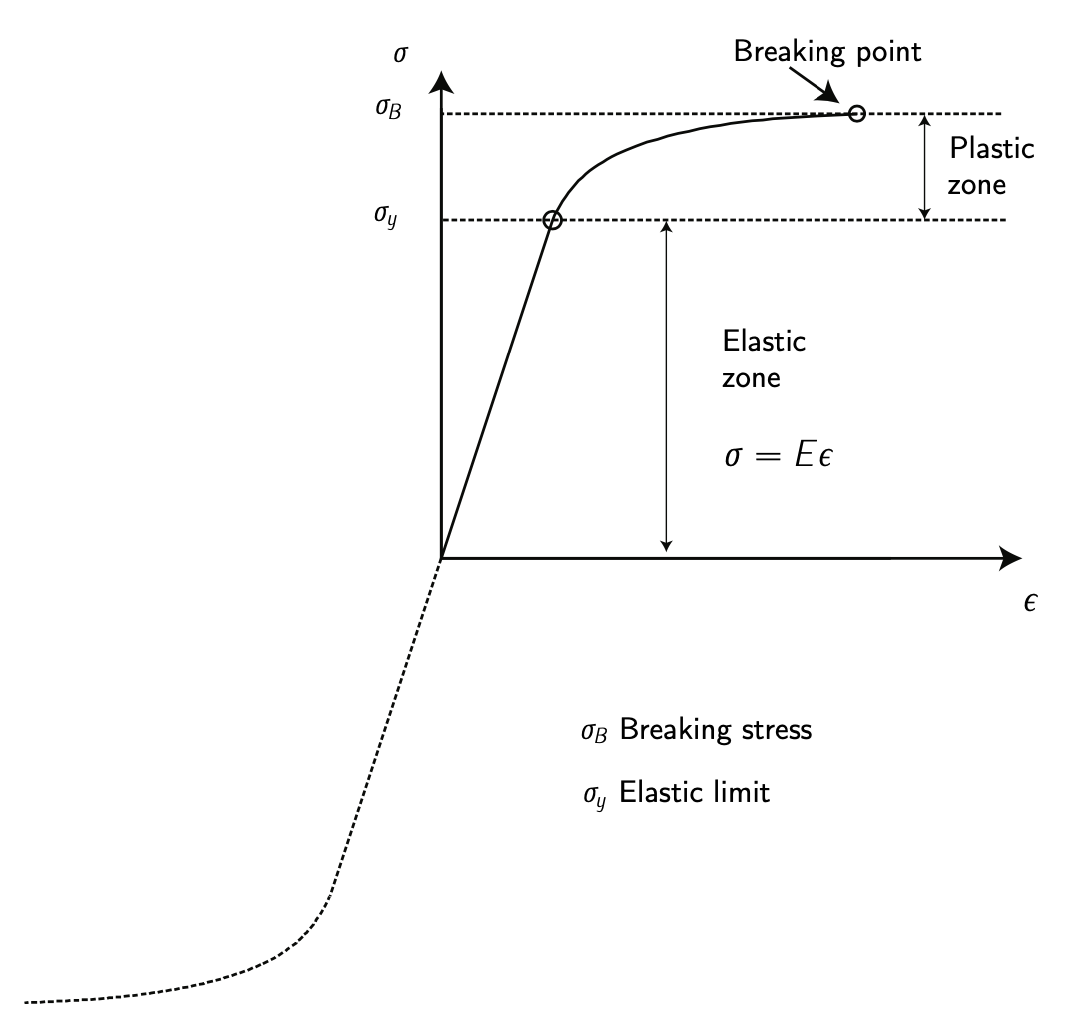
    2022-01-19 9.05.38.png
    Малюнок 4.9: Поведінка ізотропного матеріалу. Адаптовано з\(F_{\text{RANCHINI}}\) та ін. [2].

    Деформація\(\epsilon = \tfrac{\Delta l}{l_I} = \tfrac{l - l_I}{l_I}\) - це пропорційне відхилення всередині матеріалу в результаті прикладеного напруги. Не можна піддаватися стресу, не відчуваючи напруги. Для пружної деформації, яка присутня нижче межі пружності\(\sigma = E \epsilon\), застосовується закон Гука:, де\(E\) розглядається як модуль Юнга, і це властивість матеріалу. Напруження всередині конструкції повинні зберігатися нижче визначеного дозволеного рівня, залежно від вимог конструкції (загалом напруження не повинні перевищувати межі пружності\(\sigma_y\)). Див. Малюнок 4.9.