3.5: Проблеми

Вправа\(\PageIndex{1}\) Airfoils

1. В експерименті з аеродинамічною трубою було виміряно розподіл тиску над симетричним аерофолістом для кута атаки\(14^{\circ}\). Розподіл коефіцієнта тиску на intrados\(C_{pl}\), і extrados\(C_{pE}\), аеропрофілю може бути відповідно наближений наступними функціями:
   \[C_{pl} (x) = \begin{cases} 1 - 2 \tfrac{x}{c}, \ \ \ \ \ \ & 0 \le x \le \tfrac{c}{4}, \\ \tfrac{2}{3} (1 - \tfrac{x}{c} ) \ \ \ \ \ \ & \tfrac{c}{4} \le x \le c; \end{cases}\nonumber\]
   \[C_{pE} (x) = \begin{cases} - 12 \tfrac{x}{c}, \ \ \ \ \ \ & 0 \le x \le \tfrac{c}{4}, \\ 4 (-1 + \tfrac{x}{c} ) \ \ \ \ \ \ & \tfrac{c}{4} \le x \le c. \end{cases}\nonumber\]
   (а) Намалюйте криву, яка представляє розподіл тисків.
   (б) Розглядаючи хорду\(c = 1\) m, отримати коефіцієнт підйому аерозольного профілю.
   (в) Обчисліть нахил характерної кривої\(c_l (\alpha)\).
2. Виходячи з такого аерофольгу, як поперечний переріз, будуємо прямокутне крило з розмахом крил\(b = 20\)\(c = 1\) m і постійною хордою м Розподіл коефіцієнта підйому по розмаху крила (\(y\)осі) для кута атаки\(\alpha = 14^{\circ}\) наближається наступним параболічним функція:
   \[c_l (y) = 1.25 - 5 (\dfrac{y}{b})^2, - \dfrac{b}{2} \le y \le \dfrac{b}{2}.\nonumber\]
   (a) Намалюйте криву\(c_l (y)\).
   (б) Розрахувати коефіцієнт підйому крила.

Відповідь

1. 
   (а) Крива виглядає наступним чином:
   
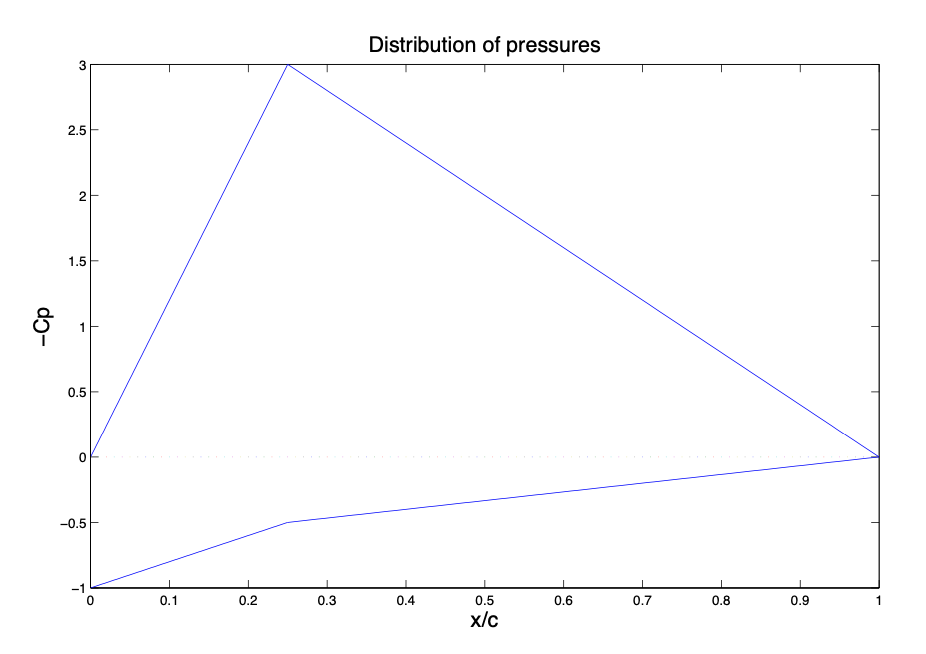
   Малюнок 3.28: Розподіл коефіцієнта тисків.
   (b) Коефіцієнт підйому для аеродрому для\(\alpha = 14^{\circ}\) може бути розрахований наступним чином:
   \[c_l = \dfrac{1}{c} \int_{x_{le}}^{x_{te}} (c_{pl} (x) - c_{pE} (x)) dx,\label{eq3.5.1}\]
   У цьому випадку при\(c = 1\) і заданих розподілах тисків Intrados і extrados, Рівняння (\(\ref{eq3.5.1}\)) стає:
   \[c_l = \dfrac{1}{c} \left [ \int_{0}^{1/4} ((1 - 2x) - (-12x)) dx + \int_{1/4}^{1} (2/3 (1 - x) - 4(-1 + x)) dx \right ] = 1.875. \nonumber\]
   (c) Характеристична крива задається:
   \[c_l = c_{l_0} + c_{l_{\alpha}} \alpha.\nonumber\]
   Оскільки аеропрофіль симетричний:\(c_{l_0} = 0\). Тому\(c_{l_{\alpha}} = \tfrac{c_l}{\alpha} = \tfrac{1.875 \cdot 360}{14 \cdot 2\pi} = 7.16 \ 1/rad\).
2. 
   (а) Крива виглядає наступним чином:
   
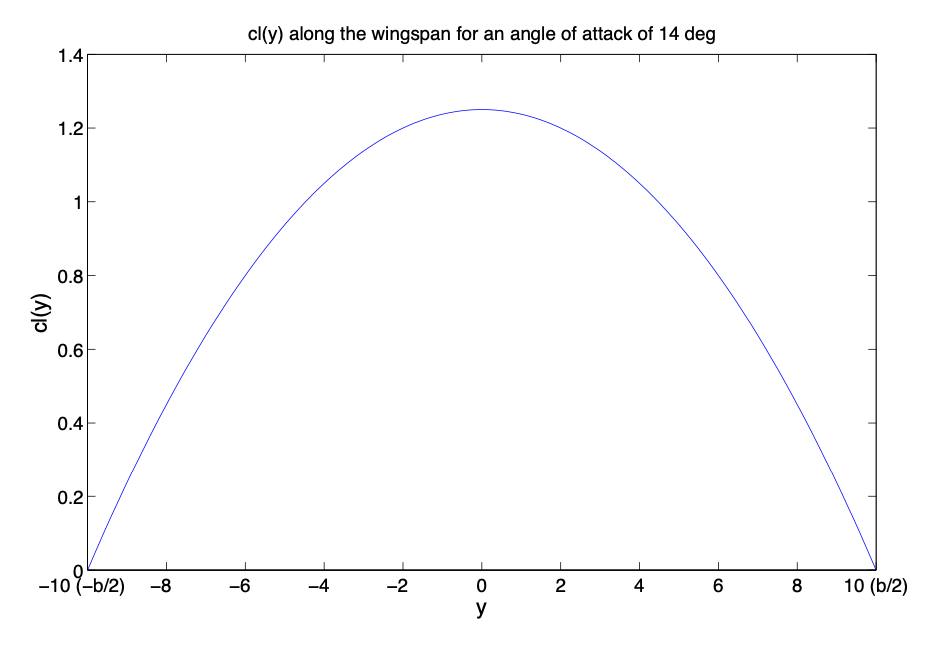
   Малюнок 3.29: Коефіцієнт підйому по розмаху крил.
   (b) Коефіцієнт підйому крила для\(\alpha = 14^{\circ}\) може бути розрахований наступним чином:
   \[C_L = \dfrac{1}{S_w} \int_{-b/2}^{b/2} c(y) c_l (y) dy.\label{eq3.5.2}\]
   Заміна в рівнянні (\(\ref{eq3.5.2}\)) враховуючи\(c(y) = 1\) і\(b = 20\):
   \[C_L = \dfrac{1}{20} \int_{-10}^{10} \left (1.25 - 5 (\dfrac{y}{20})^2 \right ) dy = 0.83.\nonumber\]

Вправа\(\PageIndex{2}\) Airfoils

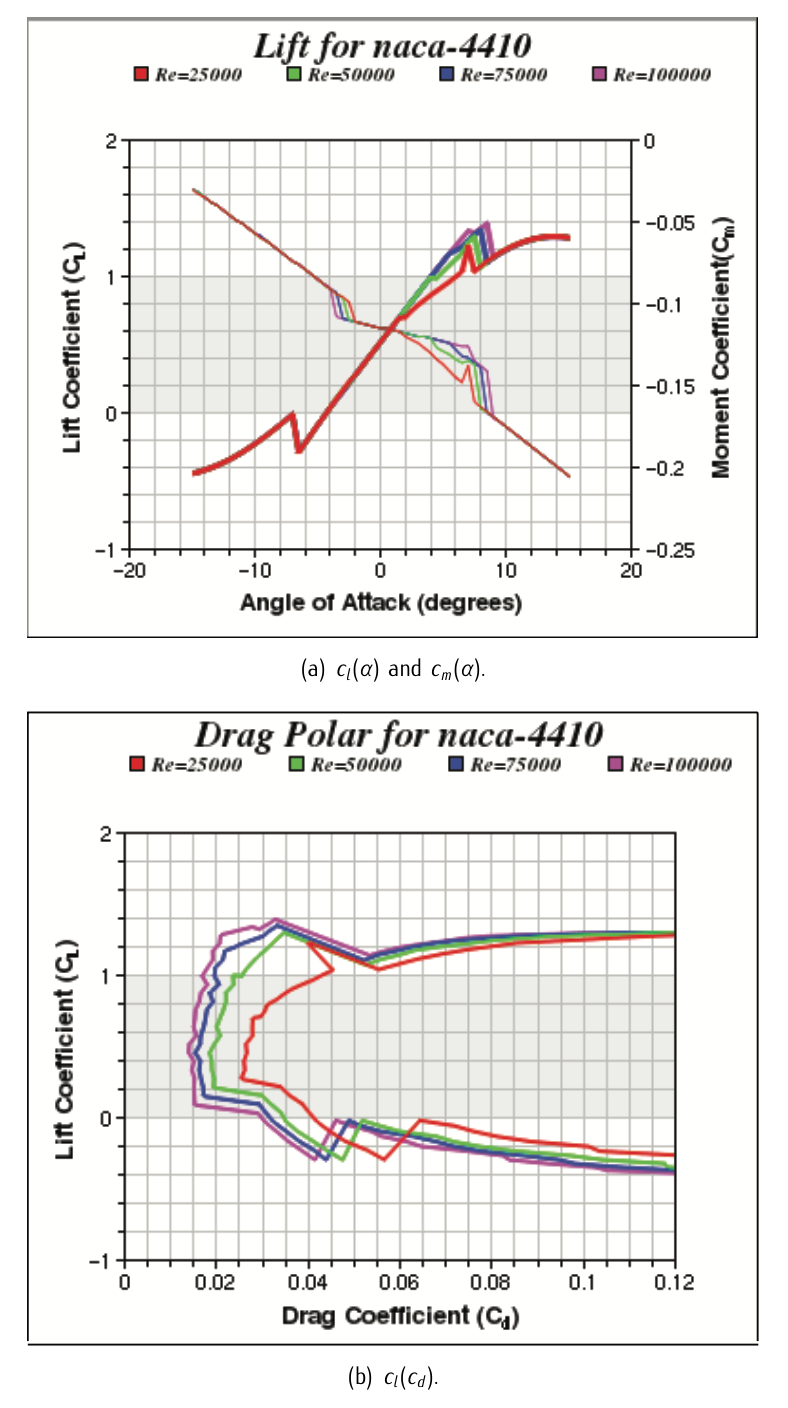
Малюнок 3.30: Характерні криві аерокрила NACA 4410.

Ми хочемо знати аеродинамічні характеристики аеродинамічного профілю NACA-4410 для числа Рейнольдса\(\text{Re} = 100000\). Експериментальні результати дали характерні криві, показані на малюнку 3.30.

Обчисліть:

1. Вираз кривої підйому в лінійному діапазоні у вигляді:\(c_l = c_{l0} + c_{l\alpha} \alpha\).
2. Вираз параболічної полярності аерокрила у вигляді:\(c_d = c_{d0} + b_{c_l} + kc_l^2.\)
3. кут атаки і коефіцієнт підйому, відповідний мінімальному коефіцієнту опору.
4. Кут атаки, коефіцієнт підйому і коефіцієнт опору, відповідний максимальному аеродинамічному ККД.
5. Значення аеродинамічних сил на одиницю довготи, які модель з хордою\(c= 2\) m виробляла б в експериментах з аеродинамічною трубою з кутом атаки\(\alpha = 3^{\circ}\) і падаючого струму з числом Маха\(M = 0.3\). Розглянемо умови ІСА на висоті\(h = 1000\) м.

Відповідь

Ми хочемо наблизити експериментальні дані, наведені на малюнку 3.30, відповідно до прямої та параболічної кривої. Тому для однозначного визначення таких кривих ми повинні вибрати:

• Дві пари точок (\(c_l, \alpha\))\(c_l (\alpha)\) кривої на малюнку 3.30.a.
• Три пари точок (\(c_l, c_d\))\(c_l (c_d)\) кривої на малюнку 3.30.b.

За малюнком 3.30 Для\(\text{Re} = 100000\) вибираємо (будь-яка інша правильно підібрана комбінація повинна працювати):

\(c_l\)	\(\alpha\)
0.5	\(0^{\circ}\)
1	\(4^{\circ}\)

Таблиця 3.3: Дата, отримана з малюнка 3.30.a.

\(c_l\)	\(c_d\)
0	0,03
1	0.0175
1.4	0.0325

Таблиця 3.4: Дані, отримані з малюнка 3.30.b.

1. Вираз кривої підйому в лінійному діапазоні у вигляді:\(c_l = c_{l0} + c_{l\alpha} \alpha\):
   З даними в таблиці 3.3:
   \[c_{l0} = 0.5;\]
   \[c_{l\alpha} = 7.16 \cdot 1/rad.\]
   Необхідна крива дає:
   \[c_l = 0.5 + 7.16 \alpha [\alpha \ in \ rad]\label{eq3.5.5}\]
2. Вираз параболічної полярності аеропрофілю у вигляді:\(c_d = c_{d0} + bc_l + kc_l^2\): За даними таблиці 3.4 ми маємо систему
   з трьох рівнянь з трьома невідомими, які підлягають розв'язанню. Це дає:
   \[c_{d0} = 0.03;\]
   \[b = -0.048;\]
   \[k = 0.0357.\]
   Вираз параболічного полярного дає:
   \[c_d = 0.03 - 0.048 c_l + 0.0357 c_l^2.\label{eq3.5.9}\]
3. Кут атаки і коефіцієнт підйому, відповідний мінімальному коефіцієнту
   опору: Для цього ми шукаємо мінімум параболічної кривої:
   \[\dfrac{dc_l}{dc_d} = 0 = b + 2 \cdot kc_l.\]
   Підставляючи в Рівняння (\(\ref{eq3.5.9}\)):
   \[\dfrac{dc_l}{dc_d} = 0 = -0.048 + 2 \cdot 0.0357 c_l \to (c_l)_{c_{d_{\min}}} = 0.672.\]
   Підставивши\((c_l)_{c_{d_{\min}}}\) в Equation (\(\ref{eq3.5.5}\)), отримаємо:
   \[(\alpha)_{c_{d_{\min}}} = 0.024\ rad (1.378^{\circ}).\nonumber\]
4. Кут атаки, коефіцієнт підйому і коефіцієнт опору, що відповідають максимальній аеродинамічній ефективності:
   Аеродинамічний ККД визначається як:
   \[E = \dfrac{l}{d} = \dfrac{c_l}{c_d}.\label{eq3.5.12}\]
   Підстановка параболічної полярної кривої в Рівняння (\(\ref{eq3.5.12}\)), отримуємо: Для
   \[E = \dfrac{c_l}{c_{d0} + bc_l + kc_l^2}.\]
   того, щоб шукати значення, відповідні максимальному аеродинамічному ККД, треба вивести і зробити його рівним нулю, тобто:
   \[\dfrac{dE}{dc_l} = 0 = \dfrac{c_{d0} - kc_l^2}{(c_{d0} + bc_l + kc_l^2)^2} \to (c_l)_{E_{\max}} = \sqrt{\dfrac{c_{d0}}{k}}.\]
   Підставляючи за значеннями раніше отримано (\(c_{d0} = 0.03, k = 0.0357\)):\((c_l)_{E_{\max}} = 0.91\). Підставивши в Рівняння (\(\ref{eq3.5.5}\)) і Рівняння (\(\ref{eq3.5.9}\)), отримаємо:
   \(\bullet (\alpha)_{E_{\max}} = 0.058\ rad\ (3.33^{\circ});\)
   \(\bullet (c_d)_{E_{\max}} = 0.01588.\)
5. Значення аеродинамічних сил на одиницю довготи, які модель з хордою\(c = 2\) m виробляла б в експериментах аеродинамічної труби з кутом атаки\(\alpha = 3^{\circ}\) і падаючого струму з числом Маха\(M = 0.3\):
   Відповідно до ISA:
   \(\bullet \rho (h = 1000) = 0.907\ kg/m^3\);
   \(\bullet a(h = 1000) = \sqrt{\gamma_{air} R (T_0 - \lambda h)} = 336.4\ m/s\);
   де a відповідає швидкості звуку,\(\gamma_{air} = 1.4, R = 287\ J/KgK, T_0 = 288.15\ k\) і\(\lambda = 6.5 \cdot 10^{-3}\).
   Оскільки експеримент призначений для\(M = 0.3\):
   \[V = M \cdot a = 100.92\ m/s.\]
   Оскільки експеримент призначений для роботи\(\alpha = 3^{\circ}\), використовуючи Equation (\(\ref{eq3.5.5}\)) та Equation (\(\ref{eq3.5.9}\)):
   \[c_l = 0.87;\]
   \[c_d = 0.01526.\]
   Нарешті:
   \[l = c_l \dfrac{1}{2} \rho c V^2 = 8036.77\ N/m;\]
   \[d = c_d \dfrac{1}{2} \rho c V^2 = 140.96\ N/m.\]

Вправа\(\PageIndex{3}\) Wings

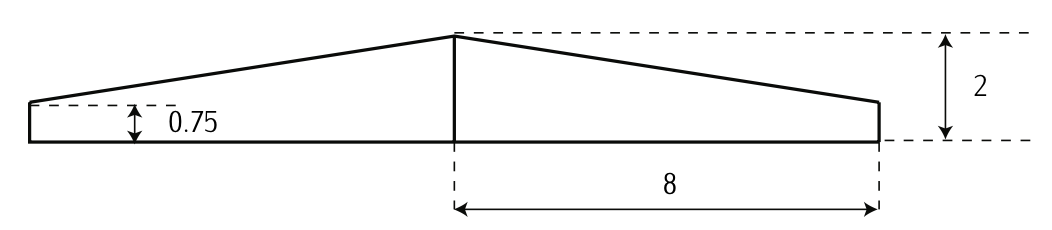
Малюнок 3.31: Рослинна форма крила (Розміри в метрах)

Ми хочемо проаналізувати аеродинамічні характеристики трапецієподібного крила з рослинною формою, як на малюнку 3.31, та коефіцієнт корисної дії крила\(e = 0.96\). Крім того, ми будемо використовувати аерозоль NACA 4415 з наступними характеристиками:

• \(c_l = 0.2 + 5.92 \alpha\).
• \(c_d = 6.4 \cdot 10^{-3} - 1.2 \cdot 10^{-3} c_l + 3.5 \cdot 10^{-3} c_l^2\).

Обчисліть:

1. Наступні параметри крила ⁴: хорда біля кореня; хорда на кінчику; середня хорда; крило-шпанл волога поверхня; збільшення.
2. Крива підйому крила в лінійному діапазоні.
3. Полярність крила припускаючи, що його можна обчислити як\(C_D = C_{D_0} + C_{D_i} C_L^2\).
4. Розрахуйте оптимальний коефіцієнт підйому\(C_{L_{opt}}\), для крила. Порівняйте його з аерофолістичним.
5. Розрахуйте оптимальний коефіцієнт опору\(C_{D_{opt}}\), для крила. Порівняйте його з аерофолістичним.
6. Максимальний аеродинамічний ККД\(E_{\max}\), для крила. Порівняйте його з аерокрилами.
7. Обговоріть відмінності\(C_{L_{opt}}\), що спостерігаються в\(C_{D_{opt}}\), і\(E_{\max}\) між крилом і аерофольгом.

Відповідь

1. Хорда біля кореня; хорда на кінчику; середня хорда; розмах крила; волога поверхня; збільшення:

За малюнком 3.31:

Розмах крила,\(b\), є\(b = 16\ m\). Акорд на ip,\(c_t\), є\(c_t = 0.75\ m\). Хорда біля кореня,\(c_r\), є\(c_r = 2\ m\).

\[C_l = C_{l_0} + C_{l_{\alpha}} \alpha.\]

Тому з рівнянням (3.67) та рівнянням (3.68) у рівнянні (3.69) ми маємо це:

Ми також можемо обчислити мокру поверхню крила, розраховуючи вдвічі більшу площу тропезоїда наступним чином:

\[S_w = 2 \left (\dfrac{(c_r + c_t)}{2} \dfrac{b}{2} \right ) = 22\ m^2.\nonumber\]

Середню хорду,\(\bar{c}\), можна обчислити як\(\bar{c} = \tfrac{S_w}{b} = 1.375\ m\); і збільшення\(A\), як\(A = \tfrac{b}{\bar{c}} = 11.63\).

2. Крива підйому крила:

Крива підйому крила може бути виражена наступним чином:

\[C_L = C_{L_0} + C_{L_{\alpha}} \alpha,\label{eq3.5.21}\]

і нахил кривої підйому крила може бути виражений пов'язаним з нахилом кривої підйому аеропрофілю як:

\[C_{L_{\alpha}} = \dfrac{C_{l_{\alpha}}}{1 + \tfrac{C_{t_{\alpha}}}{\pi A}} e = 4.89 \cdot 1/rad.\nonumber\]

Для того щоб розрахувати незалежний термін кривої підйому крила, треба враховувати той факт, що нульовий кут атаки крила збігається з нульовим кутом підйому атаки аеропрофілю, тобто:

\[\alpha (L = 0) = \alpha (l = 0).\label{eq3.5.22}\]

По-перше, зверніть увагу, що крива підйому аеропрофілю може бути виражена наступним чином

\[C_l = C_{l_0} + C_{l_{\alpha}} \alpha.\label{eq3.5.23}\]

Тому з рівнянням (\(\ref{eq3.5.21}\)) та рівнянням (\(\ref{eq3.5.22}\)) у рівнянні (\(\ref{eq3.5.23}\)) ми маємо це:

\[C_{L_0} = C_{l_0} \dfrac{C_{L_{\alpha}}}{C_{l_{\alpha}}} = 0.165.\nonumber\]

Необхідна крива дає тоді:

\[C_L = 0.165 + 4.89 \alpha [\alpha \ in \ rad].\nonumber\]

3. Вираз параболічної полярності крила:

Зверніть увагу спочатку, що постановка проблеми вказує на те, що полярний повинен бути в наступному вигляді:

\[C_D = C_{D0} + C_{D_i} C_L^2.\label{eq3.5.24}\]

Для розрахунку параболічного опору крила можна розглянути термін паразита, приблизно рівний паразитному терміні аеропрофілю, тобто\(C_{D_0} = C_{d_0}\).

\ (C_ {d_i} =\ dfrac {1} {\ pi Ae} = 0,028. \ nonномер\]

Вираз параболічного полярного дає тоді:

\[C_D = 0.0064 + 0.028 C_L^2.\label{eq3.5.25}\]

4. Оптимальний коефіцієнт підйому\(C_{L_{opt}}\),, для крила. Порівняйте його з аерокрилами.

Оптимальним коефіцієнтом підйому є те, що робить аеродинамічний ККД максимальним. Аеродинамічний ККД визначається як:

\[E = \dfrac{L}{D} = \dfrac{C_L}{C_D}.\label{eq3.5.26}\]

Підставивши параболічну полярність, задану в Рівняння (\(\ref{eq3.5.24}\)) в Рівняння (\(\ref{eq3.5.26}\)), отримаємо:

\[E = \dfrac{C_L}{C_{D_0} + C_{D_i} C_L^2}.\]

Для того щоб шукати значення, відповідні максимальному аеродинамічному ККД, потрібно вивести і зробити його рівним нулю, тобто:

\[\dfrac{dE}{dC_L} = 0 = \dfrac{C_{D_0} - C_{D_i} C_L^2}{(C_{D_0} + C_{D_i} C_L^2)^2} \to (C_L)_{E_{\max}} = C_{L_{opt}} = \sqrt{\dfrac{C_{D_0}}{C_{D_i}}}.\label{eq3.5.28}\]

Для випадку з аеродинамічним коефіцієнтом корисної дії визначається як:

\[E = \dfrac{1}{d} = \dfrac{c_l}{c_d}.\label{eq3.5.29}\]

Підставивши параболічну полярну криву, задану в твердженні у вигляді\(c_{d_0} + bc_l + kc_l^2\) в Equation (\(\ref{eq3.5.29}\)), отримаємо:

\[E = \dfrac{c_l}{c_{d_0} + bc_l + kc_l^2}.\]

Для того щоб шукати значення, відповідні максимальному аеродинамічному ККД, потрібно вивести і зробити його рівним нулю, тобто:

\[\dfrac{dE}{dC_l} = 0 = \dfrac{c_{d_0} - kc_l^2}{(c_{d0} + bc_l + kc_l^2)^2} \to (C_l)_{E_{\max}} = (c_l)_{opt} = \sqrt{\dfrac{c_{d_0}}{k}}.\label{eq3.5.31}\]

За раніше отриманими значеннями (\(C_{D_0} = 0.0064\)і\(C_{D_i} = 0.028\)) і значеннями, наведеними в заяві для полярного (\(c_{d_0} = 0.0064\),\(k = 0.0035\)) аерофольга, підставляючи їх відповідно в Equation (\(\ref{eq3.5.28}\)\(\ref{eq3.5.31}\)) і Equation () отримуємо:

• \((C_L)_{opt} = 0.478;\)
• \((c_l)_{opt} = 1.35.\)

5. Оптимальний коефіцієнт опору,\(C_{D_{opt}}\) для крила. Порівняйте його з аероплінками одного:

Після отримання оптимального коефіцієнта підйому як для аерокрила, так і для крила, просто підставляючи їх значення в обидві параболічні криві, наведені відповідно в заяві та в Equation (\(\ref{eq3.5.25}\)), отримуємо:

\[C_{D_{opt}} = 0.0064 + 0.028 C_{l_{opt}}^2 = 0.01279.\nonumber\]

\[c_{d_{opt}} = 6.4 \cdot 10^{-3} - 1.2 \cdot 10^{-3} c_{l_{opt}} + 3.5 \cdot 10^{-3} c_{l_{opt}}^2 = 0.01115.\nonumber\]

6. Максимальна аеродинамічна ефективність\(E_{\max}\) для крила. Порівняйте його з аерокрилами один:

Максимальний аеродинамічний ККД можна отримати у вигляді:

\[E_{\max_{wing}} = \dfrac{C_{L_{opt}}}{C_{D_{opt}}} = 37.\nonumber\]

\[E_{\max_{airfoil}} = \dfrac{c_{l_{opt}}}{c_{d_{opt}}} = 121.\nonumber\]

7. Обговоріть відмінності, що спостерігаються в\(C_{L_{opt}}\),\(C_{D_{opt}}\) і\(E_{\max}\) між крилом і аерофолистом.

За результатами видно, що тим часом оптимальний коефіцієнт опору аналогічний як для аерокрила, так і для крила, оптимальний коефіцієнт підйому приблизно втричі нижче, ніж у аерокрила. Очевидно, що це призводить до приблизно втричі нижчої ефективності для крила порівняно з аерофолистом.

Що це означає? Тривимірний літак, виготовлений з\(2D\) аеродромів, генерує набагато більше опору,\(2D\) ніж аеростат, щоб досягти необхідного підйому. Тому ми не можемо просто екстраполювати аналіз аеропрофілю на крило.

Така втрата ефективності обумовлена так званим індукованим перетягуванням ліфтом. Пояснення такої поведінки пов'язано з різницею тисків між екстрадосом та інтрадосом. Зокрема, в області, близькій до граничної межі, є повітряний струм, що оточує граничну межу, яка проходить від intrados, де тиск вище, до екстрадо, де тиск нижче, породжуючи два вихори, по одному в кожній межі обертаються за годинниковою стрілкою і проти годинникової стрілки. Це явище виробляє вниз за течією вихровий слід.

Наявність цього сліду модифікує подану рідину і, зокрема, змінює швидкість, яку «бачить» кожне крило аерофольги. Крім швидкості вільного потоку\(u_{\infty}\), необхідно додати вертикальну індуковану швидкість ui (див. Рис. Чим ближче до граничної межі, тим вище наведена швидкість. Тому ефективний кут атаки аерозоля нижче геометричного кута, що пояснює як зниження коефіцієнта підйому (щодо двовимірного коефіцієнта), так і поява і індукованого опору (див. Рис.

Вправа\(\PageIndex{4}\) Airfoils and Wings

1. В експерименті з аеродинамічною трубою ми виміряли розподіл тиску на симетричному аерофолисті з кутом атаки\(6^{\circ}\). Розподіли коефіцієнта тисків для інтрадо\((C_{pl})\) і екстрадо\((C_{pE})\) можна наблизити наступними функціями:
   \[C_{pl} (x) = \begin{cases} 10 \tfrac{x}{c}, \ \ \ \ \ \ \ & 0 \le \tfrac{x}{c} \le \tfrac{1}{10}, \\ 2 - 10 \tfrac{x}{c}, \ \ \ \ \ & \tfrac{1}{10} \le \tfrac{x}{c} \le \tfrac{1}{5}; \\ 0, \ \ \ \ \ \ & \tfrac{1}{5} \le \tfrac{x}{c} \le 1. \end{cases}\nonumber\]
   \[C_{pE} (x) = \begin{cases} -15 \tfrac{x}{c}, \ \ \ \ \ \ \ & 0 \le \tfrac{x}{c} \le \tfrac{1}{5}, \\ \tfrac{-15}{4} (1 - \tfrac{x}{c}, \ \ \ \ \ & \tfrac{1}{5} \le \tfrac{x}{c} \le 1. \end{cases}\nonumber\]
   (а) Намалюйте криву\(-C_p (\tfrac{x}{c})\).
   (б) Враховуючи\(c = 1 [m]\), розрахуйте коефіцієнт підйому аерозольного профілю.
2. Виходячи з попереднього профілю як поперечного перерізу, ми хочемо спроектувати прямокутне крило з розмахом крила\(b\) та постійною хордою\(c = 1\ m\). Розподіл коефіцієнта підйому вздовж прольоту крила для кута атаки\(6^{\circ}\) може бути наближений наступною функцією:
   \[c_l (y) = c_{l_{airfoil}} \cdot (1 - \dfrac{4}{A} \cdot (\dfrac{y}{b})^2), -\dfrac{b}{2} \le y \le \dfrac{b}{2},\nonumber\]
   будучи\(c_{l_{airfoil}}\) коефіцієнтом підйому аеродрому, розрахованим раніше, і A - збільшенням крила.
   (а) Обчисліть коефіцієнт підйому крила в залежності від збільшення\(A\).
   (б) Розрахувати коефіцієнт підйому крила для\(A = 1\),\(A = 8yA =\infty\).
   (c) Намалюйте розподіл коефіцієнта підйому вздовж прольоту крила для\(A = 1, A = 8yA = \infty\). Обговоріть результати.

Відповідь

1. Аерокрил:

(а) Крива виглядає наступним чином:

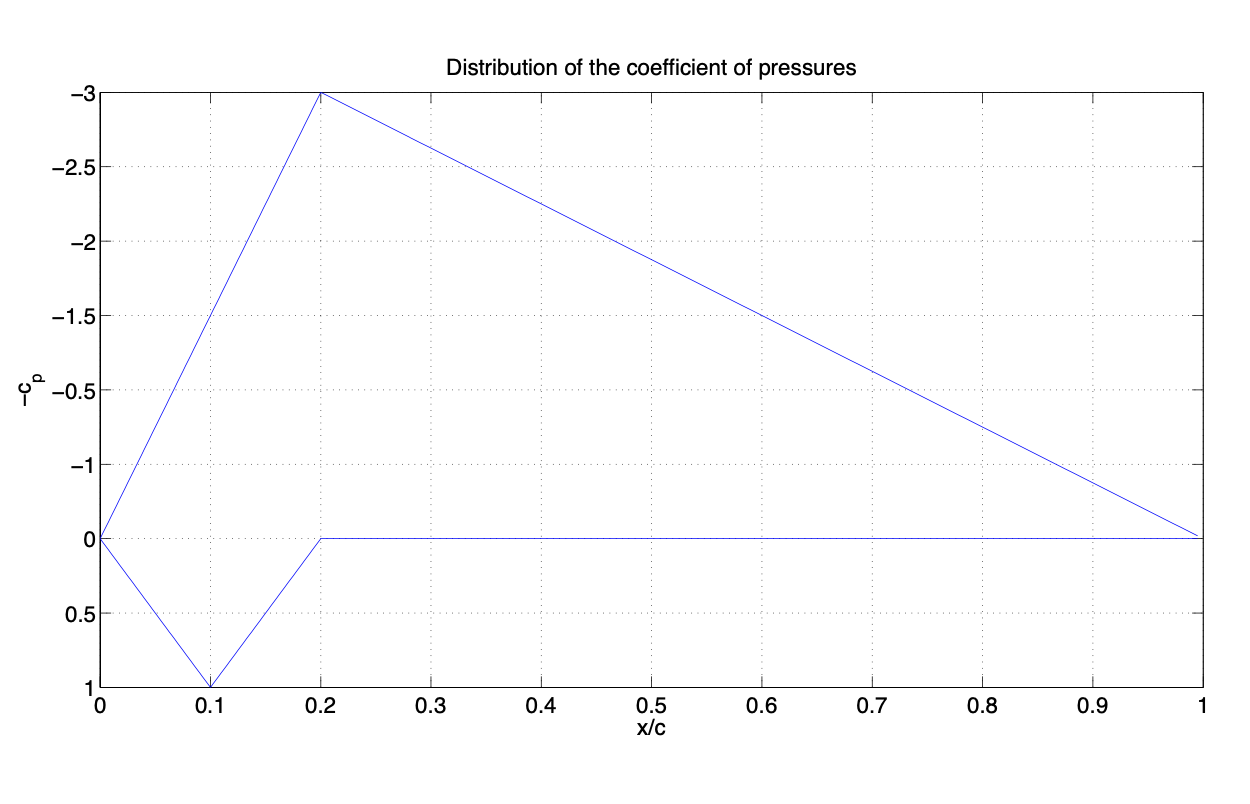
Малюнок 3.32: Розподіл коефіцієнта тисків.

(b) Коефіцієнт підйому аерозольного профілю для\(\alpha = 6^{\circ}\) можна розрахувати наступним чином:

\[c_l = \dfrac{1}{c} \int_{x_{le}}^{x_{te}} (c_{pl} (x) - c_{pE} (x)) dx.\label{eq3.5.32}\]

При цьому при\(c = 1\) і заданих розподілах тисків intrados і extrados, Equation (\(\ref{eq3.5.32}\)) стає:

\[c_l = \dfrac{1}{c} \left [\int_{0}^{1/10} (10x) dx + \int_{1/10}^{1/5} (2 - 10x) dx + \int_{1/5}^{1} (0) dx - \int_{0}^{1/5} (-15x) dx - \int_{1/5}^{1} (-15/4 (1 - x)) dx \right ] = 1.6.\nonumber\]

2. Крило:

(а) Коефіцієнт підйому крила для\(\alpha = 6^{\circ}\) можна розрахувати наступним чином:

\[C_L = \dfrac{1}{S_w} \int_{-b/2}^{b/2} c(y) c_l (y) dy.\label{eq3.5.33}\]

Підставляючи в рівняння (\(\ref{eq3.5.33}\)), враховуючи\(c(y) = 1\):

\[C_L = \dfrac{1}{b} \int_{-b/2}^{b/2} 1.6 \left (1 - \dfrac{4}{A} (\dfrac{y}{b})^2 \right ) dy = 1.6(1 - \dfrac{1}{3A}).\nonumber\]

(b) Значення\(C_L\) для різних розширень:

• \(A = 1 \to C_L = 1.06.\)
• \(A = 8 \to C_L = 1.53.\)
• \(A = \infty \to C_L = 1.6.\)

Враховуючи, наприклад, розмах крила\(b = 20\ m\), крива виглядає наступним чином:

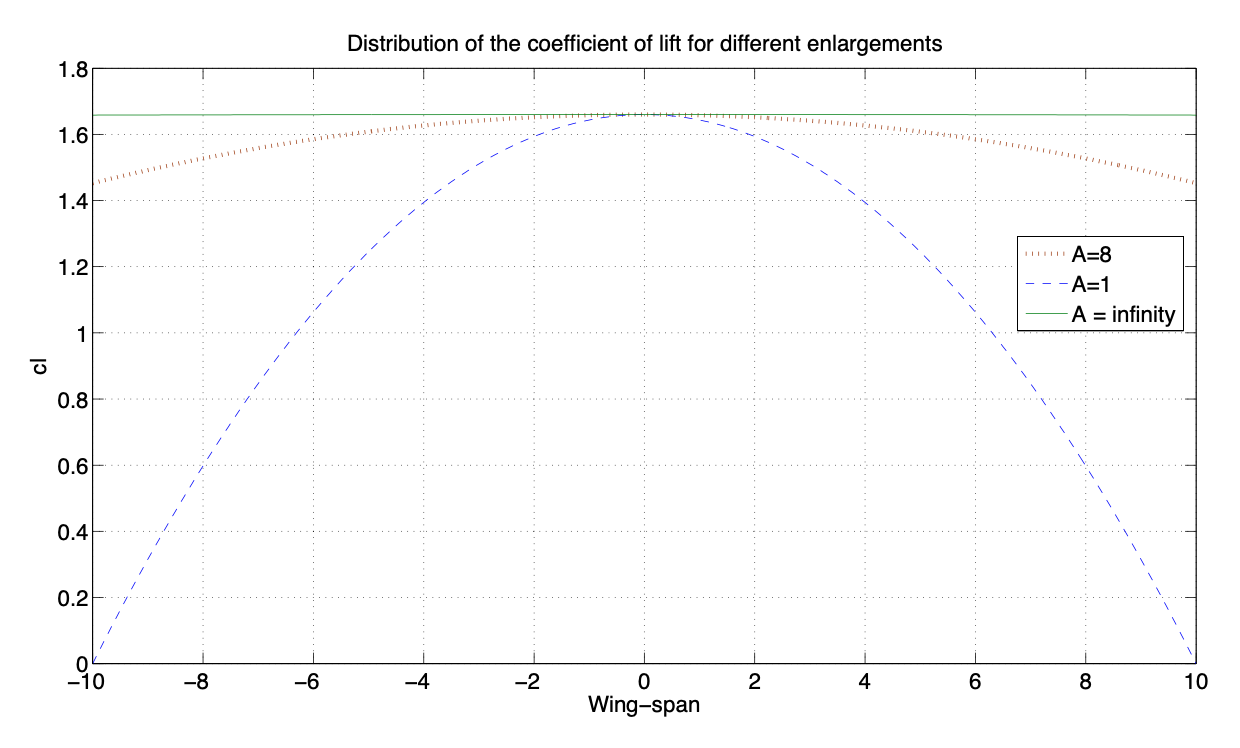
Малюнок 3.33: Коефіцієнт підйому по розмаху крил

(c) Обговорення стосується відмінностей у генерації ліфтів між кінцевим та нескінченним крилом.

Можна помітити, що якщо збільшення нескінченність, крило поводиться як двовимірна\(y (c_l(y)\) константа аеропрофілю). З іншого боку, якщо розширення кінцеве,\(c_l (y)\) показує максимум в\((y = 0)\) корені крила і йде до нуля у кінчику крила\((y/c = A/2)\). У міру зменшення збільшення максимум\(c_l(y)\) також зменшується.

Пояснення такої поведінки пов'язано з різницею тисків між екстрадосом та інтрадосом. Зокрема, в області, близькій до граничної межі, є повітряний струм, що оточує граничну межу, яка проходить від intrados, де тиск вище, до екстрадо, де тиск нижче, породжуючи два вихори, по одному в кожній межі обертаються за годинниковою стрілкою і проти годинникової стрілки. Це явище виробляє вниз за течією вихровий слід.

Наявність цього сліду змінює поле рідини і, зокрема, змінює швидкість, яку «бачить» кожне крило аерофольги. Крім швидкості вільного потоку\(u_{\infty}\), необхідно додати вертикальну індуковану швидкість (див. Рис.\(u_i\) Чим ближче до граничної межі, тим вище наведена швидкість. Тому ефективний кут атаки аеродрому нижче геометричного кута, що пояснює як зменшення коефіцієнта підйому (щодо двовимірного коефіцієнта), так і тим, що це зменшення вище при наближенні до граничної межі.

Вправа\(\PageIndex{5}\) High-Lift devices

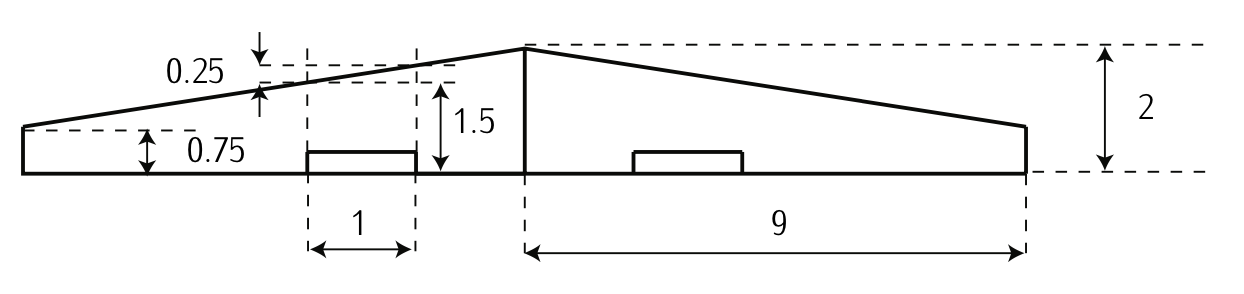
Малюнок 3.34: Рослинна форма крила (розміри в метрах).

Ми хочемо проаналізувати аеродинамічні характеристики трапецієподібного крила з рослинною формою, як на малюнку 3.34. Крило монтує дві потрійні щілинні стулки Фаулера. Коефіцієнт корисної дії (фактор Освальда) крила є\(e = 0.96\). Крило побудовано з використанням\(NACA\) аерозолів 4415 з наступними характеристиками:

• \(c_l = 0.2 + 5.92 \alpha\). (\(\alpha\)ан радіан)
• \(c_d = 6.4 \cdot 10^{-3} - 1.2 \cdot 10^{-3} c_l + 3.5 \cdot 10^{-3} c_l^2\).

Що стосується впливу стулок Фаулера на максимальний коефіцієнт підйому, то відомо, що:

• Збільшення максимального коефіцієнта підйому аерокрила (\(\Delta c_{l_{\max}}\)) можна наблизити наступним виразом:
  \[\Delta c_{l_{\max}} = 1.9 \dfrac{c'}{c},\label{eq3.5.34}\]
  бути\(c\) хордою в корені і\(c'\) розширеною хордою (розглянемо\(c' = 3\ [m]\)).
• Збільшення максимального коефіцієнта підйому крила (\(\Delta C_{L_{\max}}\)) може бути пов'язане зі збільшенням максимального коефіцієнта підйому аеродрому (\(\Delta c_{l_{\max}}\)) за допомогою наступного виразу:
  \[\Delta C_{L_{\max}} = 0.92 \Delta c_{l_{\max}} \dfrac{S_{fw}}{S_w} \cos \wedge.\label{eq3.5.35}\]

Виходячи з даних, наведених на малюнку 3.34, обчислюють:

(а) Хорда в корені і кінчику крила. Розмах крила і розширення. Мокра поверхня крила (\(S_w\)) і поверхня, змочена стулками (\(S_{fw}\)). Літак змітався (\(\wedge\)) вимірюється від передньої кромки.

Припускаючи чисту конфігурацію (відсутність відхилення заслінки), характерну для умов круїзу, а також знаючи, що стійло аеродрому відбувається під кутом атаки\(15^{\circ}\):

(б) розрахувати максимальний коефіцієнт підйому аерозольного профілю.

(c) обчислити вираз кривої підйому крила в його лінійному діапазоні.

(г) розрахувати максимальний коефіцієнт підйому крила (припустимо, що літак (крило) глухне також під кутом атаки\(15^{\circ}\))

Припускаючи конфігурацію з повністю відхиленими стулками, характерною для остаточного підходу, обчислюємо:

(е) максимальний коефіцієнт підйому крила.

Відомо, що маса літака є\(4500\ kg\). Для\(ISA\) умов рівня моря і сили за рахунок сили тяжіння дорівнює\(9.81\ m/s^2\):

(f) розрахувати швидкість зупинки літака для обох конфігурацій (чистої та повної).

(g) порівняти і обговорити результати.

Відповідь

(а). Хорда біля кореня; хорда на кінчику; розмах крила і збільшення; волога поверхня крила і волога поверхня клапоть; підмітається:

Згідно з малюнком 3.34:

• Розмах крила,\(b\), є\(b = 18\ m\).
• Акорда на кінчику,\(c_t\), є\(c_t = 0.75\ m\).
• Хорда біля кореня,\(c_r\), є\(c_r = 2\ m\).

Ми також можемо розрахувати мокру поверхню крила, обчислюючи подвійну площу трапеції наступним чином:

\[S_w = 2 \left ( \dfrac{(c_r + c_t)}{2} \dfrac{b}{2} \right ) = 24.75\ m^2.\nonumber\]

Таким же чином мокру поверхню заслінки\((S_{fw})\) можна розрахувати наступним чином:

\[S_{fw} = 2 \left ( 1 \cdot 1.5 + \dfrac{1}{2} 1 \cdot 0.25 \right ) = 3.25 \ m^2.\nonumber\]

Середню хорду,\(\bar{c}\), можна обчислити як\(\bar{c} = \tfrac{S_w}{b} = 1.375\ m\); і збільшення\(A\), як\(A = \tfrac{b}{\bar{c}} = 13.09\).

Нарешті, змітка крила (\(\wedge\)), виміряна від переднього краю, становить:

\[\wedge = \arctan (\dfrac{0.25}{1}) = 14^{\circ}.\nonumber\]

(б). \(c_{l_{\max}}\)

Відповідно до виразу, наведеного в заяві для кривої підйому аеродрому:\(c_l = 0.2 + 5.92 \alpha\), і з огляду на, що аеродроми глухне на\(\alpha = 15^{\circ}\), максимальний коефіцієнт підйому буде задаватися величиною коефіцієнта підйому під кутом стійла:

\[c_{l_{\max}} = 0.2 + 5.92 \cdot 15 \dfrac{2\pi}{360} = 1.74.\]

(c). Крива підйому крила:

Крива підйому крила може бути виражена наступним чином:

\[C_L = C_{L_0} + C_{L_{\alpha}} \alpha,\label{eq3.5.37}\]

і нахил кривої підйому крила може бути виражений пов'язаним з нахилом кривої підйому аеропрофілю як:

\[C_{L_{\alpha}} = \dfrac{C_{l_{\alpha}}}{1 + \tfrac{C_{l_{\alpha}}}{\pi A}} e = 4.96 \cdot 1/rad.\nonumber\]

Для того щоб розрахувати незалежний термін кривої підйому крила, треба враховувати той факт, що нульовий кут атаки крила збігається з нульовим кутом підйому атаки аеропрофілю, тобто:

\[\alpha (L = 0) = \alpha (l = 0).\label{eq3.5.38}\]

По-перше, зверніть увагу, що крива підйому аеропрофілю може бути виражена наступним чином

\[C_l = C_{l_0} + C_{l_{\alpha}} \alpha.\label{eq3.5.39}\]

Тому з рівнянням (\(\ref{eq3.5.37}\)) та рівнянням (\(\ref{eq3.5.38}\)) у рівнянні (\(\ref{eq3.5.39}\)) ми маємо це:

\[C_{L_0} = C_{l_0} \dfrac{C_{L_{\alpha}}}{C_{l_{\alpha}}} = 0.1678.\label{eq3.5.40}\]

Необхідна крива дає тоді:

\[C_L = 0.1678 + 4.96 \alpha \ [\alpha \ in \ rad].\nonumber\]

(г). \(C_{L_{\max}}\)в чистій конфігурації:

Враховуючи вираз в Equation (\(\ref{eq3.5.40}\)) і враховуючи, що літак (крило) зупиняється на\(\alpha = 15^{\circ}\), максимальний коефіцієнт підйому буде задаватися:

\[C_{L_{\max}} = 0.1678 + 4.96 \cdot 15 \dfrac{2\pi}{360} = 1.466.\]

(е). \(C_{L_{\max}}\)в повній комплектації (при відхиленні всіх стулок):

Для того, щоб отримати максимальний коефіцієнт підйому для повної конфігурації,\((C_{L_{\max}})\) ми маємо, що:

\[C_{L_{\max_f}} = C_{L_{\max}} + \Delta C_{L_{\max}}.\]

Як це було дано в Рівнянні (\(\ref{eq3.5.35}\)),\(\Delta C_{L_{\max}}\) може бути виражено у вигляді:

\[\Delta C_{L_{\max}} = 0.92 \Delta c_{l_{\max}} \dfrac{S_{fw}}{S_w} \cos \wedge, \nonumber\]

де\(\wedge\)\(S_{fw}\), і вже\(S_w\) відомі і\(c_{l_{\max}}\) були наведені в Equation (\(\ref{eq3.5.34}\)). Тому,\(\Delta C_{L_{\max}} = 0.334\).

\(C_{L_{\max_f}}\)врожайність тоді 1,8.

ф.\(V_{stall}\):

Знаючи про те\(L = C_L \cdot \tfrac{1}{2} \rho S_w V^2\), що політ можна вважати врівноваженим, тобто\(L = m \cdot g\), і що швидкість стійла відбувається, коли коефіцієнт підйому максимальний, ми маємо що:

\[V_{stall} = \sqrt{\dfrac{m \cdot g}{\tfrac{1}{2} \rho S_w C_{L_{\max}}}} = 44.56 \ m/s.\nonumber\]

Для випадку повної конфігурації ми використовуємо\(C_{L_{\max_f}}\) і розглядаємо вологу поверхню крила і заслінки (зверніть увагу, що ми не включаємо розширення хорди в мокрій поверхні крила). Швидкість стійла дає:

\[V_{stall_f} = \sqrt{\dfrac{m \cdot g}{\tfrac{1}{2} \rho (S_w + S_{fw}) C_{L_{\max_f}}}} = 37.8 \ m/s. \nonumber\]

г Обговорення:

Високошвидкісні пристрої призначені для збільшення максимального коефіцієнта підйому. Своїм розгортанням вони збільшують аеродинамічну хорду та розвал аеродинамічного профілю, змінюючи таким чином геометрію аеропрофілю, щоб швидкість стійла під час певних етапів польоту, таких як посадка або зліт, значно зменшується, що дозволяє літати повільніше, ніж у круїзі.

Розгортання високошвидкісних пристроїв також збільшує коефіцієнт опору літака. Тому при будь-якій заданій вазі і швидкості повітря відхилені заслінки збільшують силу опору. Стулки збільшують коефіцієнт опору літака через більш високий індукований опір, спричинений спотвореним розподілом підйому на крилі з розширеними клапанами. Деякі пристрої збільшують площинуформу крила, і при будь-якій заданій швидкості це також збільшує паразитарну складову опору загального опору.

Зменшуючи робочу швидкість та збільшуючи опору, пристрій високого підйому скорочує відстані зльоту та посадки, а також покращує швидкість підйому. Тому ці пристрої є основоположними під час зльоту (зменшують швидкість, з якою підйомники літака дорівнює вазі літака), під час початкової фази підйому (збільшує швидкість підйому, щоб можна було уникнути перешкод) і посадки (зменшити швидкість удару і допомогти гальмувати літак).

---

4. Виходячи з наведених даних на малюнку 3.31.