Skip to main content
LibreTexts - Ukrayinska

16.5: Подальші теми

  1. Last updated
  2. Save as PDF
  • Page ID
    75044

    • Boundless
    • Boundless
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    навчальні цілі

    • Визначте джерела сферичних і плоских хвильових моделей

    сферичні хвилі

    Крістіан Гюйгенс був голландським вченим, який розробив корисну методику визначення того, як і де поширюються хвилі. У 1678 році він запропонував, щоб кожна точка, до якої торкається світлове збудження, сама по собі стає джерелом сферичної хвилі; сума цих вторинних хвиль визначає форму хвилі в будь-який наступний час. Принцип Гюйгена-Френеля показує, що коли хвилі взаємодіють один з одним, вони заважають або конструктивно, або руйнівно. Конструктивне втручання виникає, коли хвилі повністю перебувають у фазі один з одним і посилюють хвилі. Руйнівні перешкоди виникають, коли хвилі точно виходять з фази з будь-якими іншими, і якщо хвилі ідеально виходять з фази один з одним, хвиля буде скасована повністю. Оскільки хвилі походять від одного точкового джерела, хвилі відбуваються сферичним малюнком. Всі хвилі надходять від одного точкового джерела і мають сферичну форму.

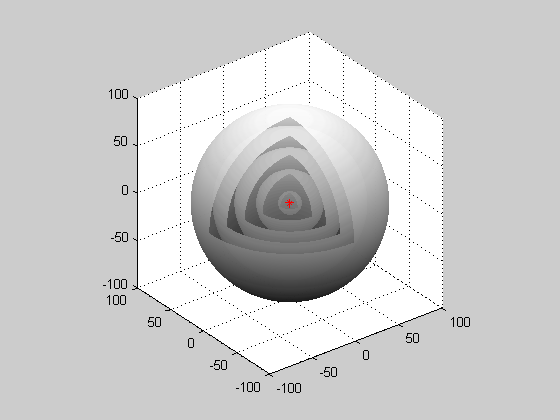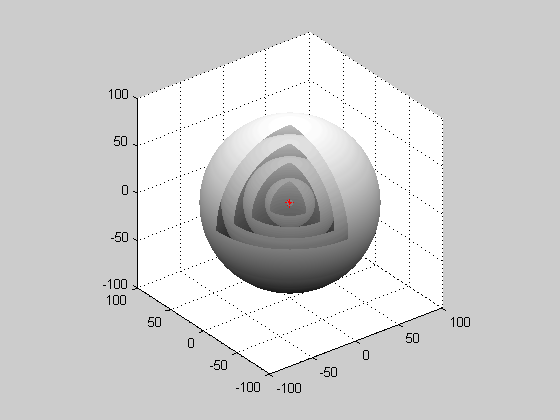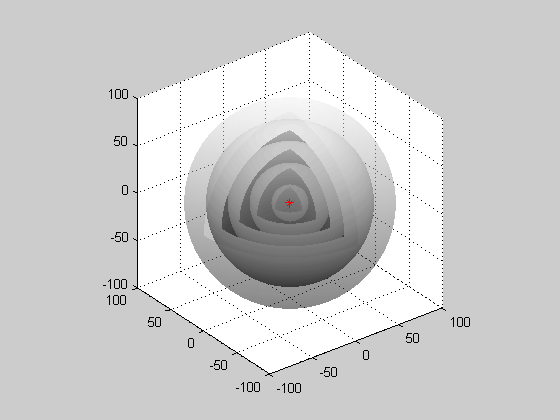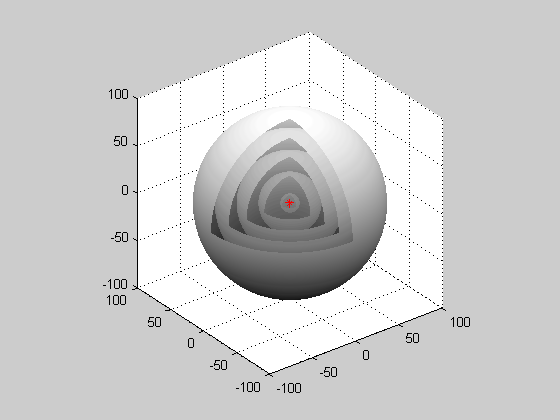
    зображення

    Сферична хвиля: Коли хвилі виробляються з точкового джерела, вони є сферичними хвилями.

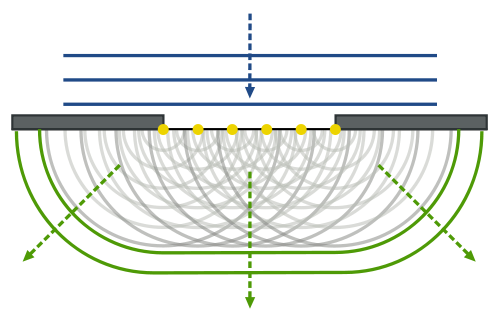
    зображення

    Принцип Гюйгена-Френеля: Принцип Гюйгена-Френеля використовує закон заломлення. Кожна точка на хвилі виробляє хвилі, які заважають один одному або конструктивно, або руйнівно.

    Площинні хвилі

    Плоска хвиля - це хвиля постійної частоти, хвилі якої (поверхні постійної фази) є нескінченними паралельними площинами постійної амплітуди від піку до піку, нормальної вектору фазової швидкості. На практиці неможливо мати справжню плоску хвилю; лише плоска хвиля нескінченної протяжності поширюватиметься як плоска хвиля. Однак багато хвиль - це приблизно плоскі хвилі в локалізованій області простору. Наприклад, локалізоване джерело, таке як антена, виробляє поле, яке приблизно плоска хвиля далеко від антени в області далекого поля. Аналогічно, якщо шкали довжини набагато довші, ніж довжина хвилі хвилі, як це часто буває для світла в області оптики, можна розглядати хвилі як світлові промені, які відповідають локально плоским хвилям.

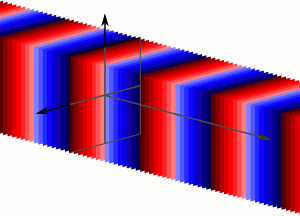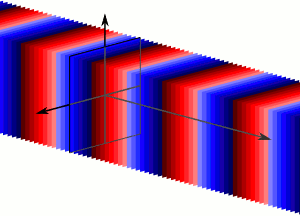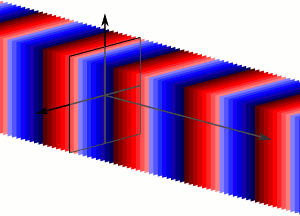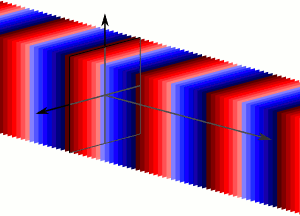
    зображення

    Плоска хвиля: Плоскі хвилі - це нескінченна кількість хвильових фронтів, нормальних до напрямку пропогації.

    Стоячи хвилі на струні

    Стояча хвиля виникає за рахунок перешкод, коли поперечні хвилі в струн відбиваються і зустрічаються падаючі і відбиті хвилі.

    навчальні цілі

    • Визначте, коли виникає стояча хвиля

    Стояча хвиля - це хвиля, яка здається нерухомою, тобто вона залишається в постійному положенні. У струні стояча хвиля - це тип поперечної хвилі, де рух частинок середовища перпендикулярно напрямку поширення хвилі. Стояча хвиля може виникнути, коли заважають дві однакові хвилі, що рухаються в різні боки уздовж струни.

    Існує два сценарії хвиль у струн: струна закріплюється з обох кінців, або струна закріплена на одному кінці і вільна на іншому. Поперечна хвиля буде рухатися уздовж струни, поки не дійде до іншого кінця. Потім він відбивається від цього кінця і починає рухатися назад у вихідному напрямку; в цій точці виникають перешкоди. показує поперечну хвилю, яка відбивається від нерухомого кінця. Коли поперечна хвиля зустрічається з нерухомим кінцем, хвиля відбивається, але перевернута. Це міняє вершини з коритами, а жолоби з вершинами. діаграми поперечної хвилі на нитці, яка зустрічається з вільним кінцем. Хвиля відбивається, але на відміну від поперечної хвилі з нерухомим кінцем вона не перевернута.

    зображення

    Відображення вільного кінця: Хвиля відбивається, але на відміну від поперечної хвилі з фіксованим кінцем, вона не інвертується.

    зображення

    Фіксоване відображення кінця: Коли поперечна хвиля зустрічається з фіксованим кінцем, хвиля відбивається, але перевернута.

    стоячі хвилі

    Коли відбувається будь-який з двох сценаріїв відбиття хвилі, падаюча хвиля зустрічається з відбитою хвилею. Ці хвилі рухаються повз один одного в протилежних напрямках, викликаючи перешкоди. Коли ці дві хвилі мають однакову частоту, твір цього називається стоячими хвилями. Стоячі хвилі, здається, стоять на місці, звідси і назва. ілюструє дуже повільну рухому стоячу хвилю. (Одне застосування принципу стоячих хвиль - це музика з концепцією резонансу - і скільки музичних інструментів, таких як гітари та піаніно, отримують своє звучання.) Давайте тепер розглянемо, як виникають стоячі хвилі.

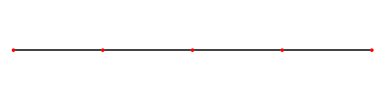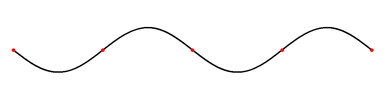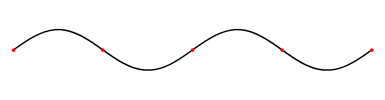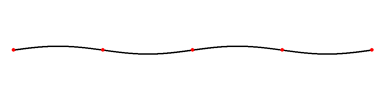
    зображення

    Стояча хвиля на струні: Це те, що стояча хвиля буде виглядати, якби ви були, щоб уповільнити його. Хвиля викликана падаючою хвилею на струні відбивається, а потім рухається назад у напрямку, звідки вона прийшла. Потім дві хвилі зустрічаються і заважають один одному, викликаючи це явище.

    Конструктивне проти руйнівного втручання

    Коли падаюча хвиля і відбита хвиля вперше зустрічаються, обидві хвилі мають амплітуду дорівнює нулю. Оскільки хвилі продовжують рухатися повз один одного, вони продовжують заважати один одному, або конструктивно, або руйнівно. Як обговорювалося в попередніх атомах, коли хвилі повністю перебувають у фазі і конструктивно заважають один одному, вони посилюються, а коли вони повністю поза фазою і заважають руйнівно, вони скасовуються. Оскільки хвилі продовжують рухатися повз один одного і відбиваються від протилежного кінця, вони продовжують заважати обом напрямкам; створюється стояча хвиля. Кожна точка в середовищі, що містить стоячу хвилю, коливається вгору і вниз, а амплітуда коливань залежить від місця розташування точки. Коли ми спостерігаємо стоячу хвилю на струн, виявляється, що хвиля не рухається, а стоїть на місці. Підсумовуючи:

    • Точки, які досягають максимальної висоти коливань, називаються антинодами і є результатом повного конструктивного втручання.
    • Точки в стоячій хвилі, які, здається, залишаються плоскими і не рухаються, називаються вузлами. Це пов'язано з повним руйнівним втручанням.

    Стоячи хвилі в повітряні колони

    Стоячі хвилі в повітряних колонках - це фізичне явище, яке надає духовим інструментам їх резонанс і, отже, звук.

    навчальні цілі

    • Визначте тип стоячої хвилі в повітряному стовпі

    стоячі хвилі

    Стояча хвиля - це хвиля, яка здається нерухомою, тобто вона залишається в постійному положенні. У повітряному стовпі стояча хвиля може утворюватися як поздовжня, так і поперечна хвиля. Поперечна хвиля, ви можете пам'ятати, - це хвиля, де рух частинок середовища перпендикулярно напрямку поширення хвилі. Поздовжня хвиля, з іншого боку, паралельна напрямку поширення. Стояча хвиля може виникнути, коли заважають дві однакові хвилі, що рухаються в різні боки.

    Повітряні колони

    Коли в трубці утворюється стояча хвиля, стояча хвиля має максимальне переміщення повітря на відкритому кінці, яке називається антинодом. Тут рух невимушено. На закритому кінці немає зміщення; це називається вузлом, і повітря зупиняється. Відстань від вузла до антінода становить 1/4 довжини хвилі і дорівнює довжині трубки.

    показує, що цей резонанс може бути створений вібрацією, введеною на закритому кінці трубки або поблизу нього. Це вважається природною вібрацією повітряного стовпа незалежно від того, як вона індукується. Враховуючи, що максимальні переміщення повітря можливі на відкритому кінці і відсутні на закритому кінці, існують інші, більш короткі довжини хвиль, які можуть резонувати в трубці. Наприклад, стояча хвиля може мати три чверті своєї довжини хвилі в трубці, або L = (3/4) λ. Це можна зробити наступним чином:

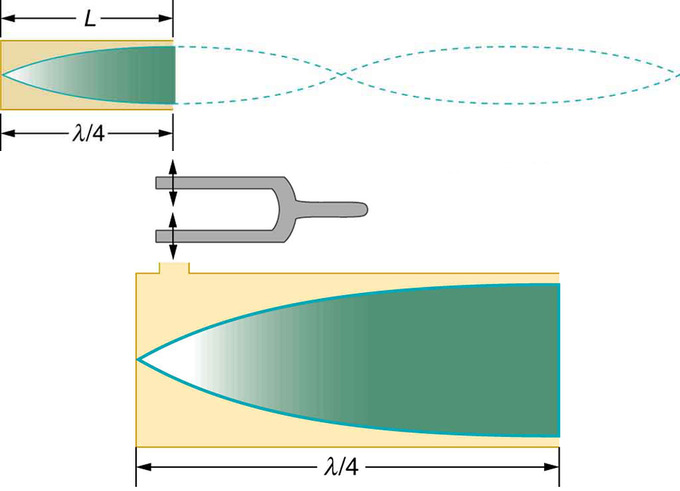
    зображення

    Стояча хвиля в повітряній колоні: Та ж стояча хвиля створюється в трубці вібрацією, введеною поблизу її закритого кінця.

    \[\lambda ^ { \prime } = \dfrac { 4 \mathrm { L } } { 3 }\]

    Продовження цього процесу виявляє цілу серію короткохвильових і високочастотних звуків, які резонують у трубці. Ми використовуємо конкретні терміни для резонансів у будь-якій системі. Найнижча резонансна частота називається фундаментальною, тоді як всі вищі резонансні частоти називаються обертонами. Всі резонансні частоти є інтегральними кратними фундаментальним, і вони в сукупності називаються гармоніками. Фундаментальним є перша гармоніка, перший обертон - друга гармоніка і так далі. показує, як основні і перші три обертони (перші чотири гармоніки) в трубці, закритій на одному кінці.

    зображення

    Перші чотири гармоніки: Основний і три найнижчі обертони для трубки, закритої на одному кінці. Всі вони мають максимальні переміщення повітря на відкритому кінці і жодного на закритому кінці.

    Тепер давайте пошукаємо закономірність в резонансних частотах для простої трубки, яка замкнута одним кінцем. Фундаментальний має = 4L, а частота пов'язана з довжиною хвилі та швидкістю звуку, як зазначено наступним:

    \[\mathbf { v } _ { \mathrm { w } } = \mathrm { f } \lambda\]

    Розв'язування для f в цьому рівнянні дає більш корисний вигляд:

    \[\mathrm { f } = \dfrac { \mathrm { v } _ { \mathrm { w } } } { \lambda } = \dfrac { \mathbf { v } _ { \mathrm { w } } } { 4 \mathrm { L } }\]

    Тут f - частота, v w - швидкість звуку в повітрі, λ - довжина хвилі, а L - довжина повітряного стовпа. Перший обертон має = 4L/3. З цього можна вивести наступне:

    \[\mathrm { f } ^ {\prime } = 3 \dfrac { v _ { \mathrm { w } } } { 4 \mathrm { L } } = 3 \mathrm { f }\]

    Оскільки f′ = 3f, ми називаємо перший обертон третьою гармонікою. Продовжуючи цей процес, ми бачимо закономірність, яку можна узагальнити в єдиному виразі. Резонансні частоти трубки, замкнутої на одному кінці, є:

    \[\mathrm { f } _ { \mathrm { n } } = \mathrm { n } \dfrac { \mathrm { vw } } { 4 \mathrm { L } } , \mathrm { n } = 1,3,5\]

    Тут f1 - фундаментальний, f3 - перший обертон і так далі. Цікаво, що резонансні частоти залежать від швидкості звуку і, отже, від температури. Ця залежність створює помітну проблему для органів у старих неопалюваних соборах, і це також причина, чому музиканти зазвичай приносять свої духові інструменти до кімнатної температури, перш ніж грати на них.

    Приклад\(\PageIndex{1}\):

    Фундаментальні і обертони можуть бути присутніми одночасно в самих різних поєднаннях. Наприклад, середній С на трубі має звук, чітко відрізняється від середнього C на кларнеті, обидва інструменти є модифікованими версіями трубки, закритої на одному кінці. Фундаментальна частота однакова (і зазвичай найінтенсивніша), але обертони та їх поєднання інтенсивності різні і підлягають затіненню музикантом. Цей мікс - це те, що надає різним музичним інструментам (і людським голосам) свої відмінні характеристики, незалежно від того, є вони повітряні колонки, струни, звукові коробки або барабанні головки. Насправді значна частина нашої мови визначається формуванням порожнини, утвореної горлом і ротом, і позиціонуванням мови для коригування фундаментальних та комбінаційних обертонів. Наприклад, прості резонансні порожнини можуть резонувати зі звуком голосних.

    Вимушені вібрації та резонанс

    Явище водіння системи з частотою, рівною її власній частоті, називається резонансом.

    навчальні цілі

    • Поясніть взаємозв'язок між резонансною кривою і демпфуванням

    Примусова вібрація та резонанс

    Багато людей грали з іграшками за участю предмета, підтримуваного гумкою: щось на зразок кульки весла, підвішеного на пальці. Скажімо, людина водить весло м'яч, рухаючи його або її палець вгору і вниз з певною частотою. У цьому прикладі він викликає вимушене коливання (або вібрацію). Спочатку палець тримається стійко, а м'яч відскакує вгору-вниз з невеликою кількістю демпфування. Якщо палець рухається вгору і вниз повільно, м'яч буде слідувати вздовж, не підстрибуючи багато самостійно.

    зображення

    Кулі та частоти весла: Куля весла на гумці рухається у відповідь на палець, що підтримує його. Якщо палець рухається з власною частотою f0 м'яча на гумці, то досягається резонанс, і різко збільшується амплітуда коливань м'яча. При більш високих і нижчих частотах руху енергія передається м'ячу менш ефективно, і він реагує коливаннями меншої амплітуди.

    У міру збільшення частоти, з якою палець рухається вгору і вниз, м'яч буде реагувати коливанням зі збільшенням амплітуди. Після руху м'яча на своїй власній частоті коливання кулі збільшуються в амплітуді з кожним коливанням до тих пір, поки він приводиться в рух. Явище водіння системи з частотою, рівною її власній частоті, називається резонансом. Оскільки частота руху стає поступово вищою, ніж резонансна або власна частота, амплітуда коливань стає меншою, поки коливання майже не зникнуть, а палець просто рухається вгору і вниз з невеликим впливом на м'яч.

    Ефекти демпфування

    У реальному житті більшість осциляторів мають демпфування, присутнє в системі. Цікаво, що ширини резонансних кривих, показаних в, залежать від демпфування: чим менше демпфування, тим вужче резонанс. Щоб керований генератор резонував на дуже конкретній частоті, має бути якомога менше демпфування, як це відбувається для фортепіано струн та багатьох інших музичних інструментів. І навпаки, для коливань невеликої амплітуди, таких як в системі підвіски автомобіля, має бути сильне демпфування. Важке демпфування зменшує амплітуду, але компроміс полягає в тому, що система реагує на більшій кількості частот.

    зображення

    Демпфування: Амплітуда гармонічного генератора є функцією частоти рушійної сили. Криві представляють один і той же генератор з однаковою власною частотою, але з різною кількістю демпфування. Резонанс виникає, коли частота водіння дорівнює власній частоті, а найбільший відгук - для найменшої кількості демпфування. Найвужча реакція також на найменшу кількість демпфування.

    Приклад\(\PageIndex{2}\):

    Ці особливості керованих гармонічних осциляторів застосовуються до величезної різноманітності систем. Наприклад, під час налаштування радіо люди регулюють резонансну частоту радіоланцюга так, щоб вона коливалася лише до частоти мовлення (або водіння) потрібної станції. Чим більш вибірковим є радіо в розрізненні станцій, тим менше його демпфування. Дитина на гойдалках рухається батьком на власній частоті гойдалки для досягнення максимальної амплітуди. У всіх цих випадках ефективність передачі енергії від рушійної сили в генератор найкраща при резонансі. На гравійних дорогах, які є рифленими, якщо люди подорожують з «неправильною» швидкістю, нерівності дуже помітні. На інших швидкостях відчути нерівності взагалі важко. показана фотографія відомого прикладу (Міст Такома звужується) руйнівного впливу веденого гармонійного коливання. На жаль, шквальні вітри довелося проганяти міст на своїй природній частоті, що призвело до обвалу.

    зображення

    Крах Такома звужує міст: У 1940 році обвалився міст Такома звужується в штаті Вашингтон. Сильні поперечні вітри привели міст до коливань на його резонансній частоті. Демпфування зменшилося, коли опорні кабелі зламалися і почали ковзати по вежах, дозволяючи все більше амплітуд, поки конструкція не вийшла з ладу. (Кредит: Студія PRI 360, через Flickr)

    Ключові моменти

    • Хвилі або заважають один одному конструктивно або руйнівно, що буде або посилювати, або мінімізувати хвилю відповідно.
    • Сферичні хвилі випромінюються від одного точкового джерела сферичної форми.
    • Плоска хвиля - це хвиля постійної частоти, хвилі якої (поверхні постійної фази) є нескінченними паралельними площинами постійної амплітуди від піку до піку, нормальної вектору фазової швидкості.
    • Хоча на практиці неможливо мати справжню плоску хвилю, багато хвиль наближають поведінку плоских хвиль.
    • Відбита хвиля інвертується від падаючої хвилі, коли поперечна хвиля на струні закріплюється в кінцевій точці. Відбита хвиля не інвертується від падаючої хвилі, коли поперечна хвиля на струні вільна в кінцевій точці.
    • Стояча хвиля виникає, коли падаюча хвиля зустрічає відбиту хвилю на струні.
    • Стояча хвиля містить вузли (точки, які залишаються рівними через руйнівну інтерференцію) та антиноди (точки з максимальним коливанням внаслідок конструктивного втручання).
    • Кожна точка в струні коливається вгору і вниз і амплітуда коливань залежить від місця розташування точки.
    • Стояча хвиля має деякі точки, які залишаються рівними через руйнівні втручання. Вони називаються антинодами.
    • Точки на стоячій хвилі, які досягли максимального коливання, роблять це від конструктивного втручання, і називаються вузлами.
    • Стояча хвиля в повітряному стовпі - це поперечна хвиля.
    • Вузол виникає на закритому кінці повітряної трубки, де немає зміщення хвилі.
    • Антинод виникає на відкритому кінці повітряної трубки, де відбувається максимальне зміщення.
    • Резонансні частоти трубки, замкнутої на одному кінці, такі:\(\mathrm { f } _ { \mathrm { n } } = \mathrm { n } \frac { \mathrm { vw } } { 4 \mathrm { L } }\), n = 1,3,5.
    • Будь-осцилятор має природну частоту. Ведуться на власній частоті, коливання збільшуються в амплітуді з кожним коливанням.
    • Ширини резонансних кривих залежать від демпфування: менша демпфування відповідає більш вузькому резонансу. При меншому затуханні пік резонансу стає більш вираженим.
    • Взаємозв'язок між резонансом і демпфуванням застосовується до величезної різноманітності систем. Демпфування часто зменшується або посилюється, щоб викликати бажану реакцію генератора.

    Ключові умови

    • хвильовий фронт: уявна поверхня, що проходить через точки середовища, що коливається у фазі.
    • деструктивні втручання: виникає, коли хвилі заважають один одному гребінь до корита (пік до долини) і точно поза фазою один з одним.
    • конструктивне втручання: Відбувається, коли хвилі заважають один одному гребінь гребеня, а хвилі точно перебувають у фазі один з одним.
    • поперечна хвиля: Будь-яка хвиля, в якій напрямок порушення перпендикулярно напрямку руху.
    • власна частота: Частота, з якою система вібрує самостійно. Для пружини (постійної пружини k) з приєднаним об'єктом маси m власна частота задається як\(\mathrm { f } _ { \mathrm { n } } = \frac { 1 } { 2 \pi } \sqrt { \frac { \mathrm { k } } { \mathrm { m } } }\).
    • демпфування: Зменшення величини коливань за рахунок розсіювання енергії

    ЛІЦЕНЗІЇ ТА АВТОРСТВА

    CC ЛІЦЕНЗОВАНИЙ КОНТЕНТ, РАНІШЕ ДІЛИВСЯ

    CC ЛІЦЕНЗОВАНИЙ ВМІСТ, СПЕЦИФІЧНА АТРИБУЦІЯ