4.3: Парне виробництво

Last updated
Save as PDF

Page ID: 79204

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Крім фотоефекту (поглинання фотонів) і розсіювання Комптона (розсіювання фотонів), існує третій процес, за допомогою якого фотони можуть втрачати енергію при взаємодії з речовиною. У цьому процесі, який називається парним виробництвом, фотон може просто зникнути, і на його місці може з'явитися пара частинок речовини-антиречовина. Це явище є чудовою ілюстрацією того, що маса не зберігається, так як маса електрона і позитрона може створюватися з енергії безмасового фотона. Звичайно, фотон повинен володіти достатньою енергією для створення інших мас двох нових частинок.

Зазвичай цей процес відбувається поблизу ядра і утворюється електрон-позитронна пара. Ефект намальований нижче:

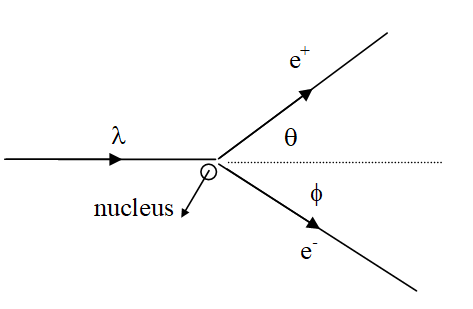
Малюнок_4.3.1.PNG

Спочатку спробуємо уявити більш просту версію цього явища, де немає ядра, а електрон і позитрон рухаються в тому ж напрямку, що і початковий фотон. Енергозбереження призведе до:

\[ E_{photon} = E_{electron} + E_{positron}\]

і збереження x-імпульсу:

\[ pc_{photon} = pc_{electron} + pc_{positron} \]

Використання

\[ E_{total}^2 = (pc)^2 + (mc^2)^2\]

енергозбереження можна записати як:
\[\sqrt{pc_{photon}^2+(0)^2} = \sqrt{pc_{electron}^2+0.511^2}+\sqrt{pc_{photon}^2 +0.511^2}\]

\[pc_{photon} = \sqrt{pc_{electron}^2+0.511^2}+\sqrt{pc_{photon}^2 +0.511^2}\]

Встановлення цього рівняння рівняння збереження імпульсу призводить до:

\[ \sqrt{ pc_{electron}^2 + 0.511^2} + \sqrt{pc_{positron}^2 +0.511^2} = pc_{electron} + pc_{electron}\]

Сподіваюся, зрозуміло, що це рівняння - сміття! Ліва частина рівняння більша за праву частину рівняння для будь-яких реальних значень імпульсу. Це означає, що розглянутий вище «спрощений» варіант парного виробництва неможливий. Єдиний спосіб виробництва пари може відбутися, якщо третє тіло (ядро) присутнє для участі в обміні енергії та імпульсу.

Однак, якщо ми спробуємо встановити та вирішити закони збереження для реального процесу виробництва пари, ми загрузнемо в досить великій кількості алгебри. Натомість давайте зробимо наближення, що оскільки ядро набагато, набагато масивніше, ніж електрон і позитрон, воно може «поглинати» належну кількість імпульсу, щоб гарантувати збереження імпульсу, не «поглинаючи» дуже багато кінетичної енергії. У певному сенсі ми будемо ігнорувати ядро під час вирішення проблеми, а потім, як тільки ми отримаємо рішення, ми перевіримо, чи ігнорування ядра було розумним вибором.

Як приклад розглянемо проблему нижче.

Приклад\(\PageIndex{1}\)

Фотон 3,0 МеВ взаємодіє з свинцевим ядром і створює електрон-позитронну пару. Електрон і позитрон рухаються перпендикулярно початковому напрямку руху фотона.

Знайдіть кінетичні енергії електрона і позитрона, припускаючи, що ядро знаходиться в стані спокою після зіткнення.
Знайдіть кінетичну енергію свинцевого ядра, необхідну для забезпечення збереження імпульсу. Чи сильно вплине ця кількість кінетичної енергії на результат у частині a?

Рішення

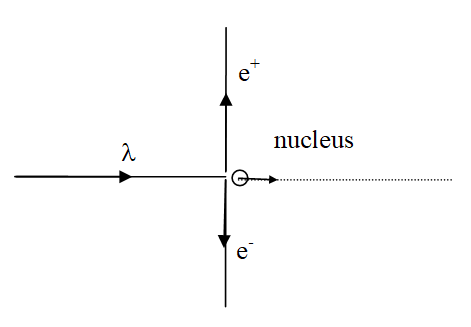
Малюнок_4.3.2.PNG

Енергозбереження (ігнорування енергії ядра) призводить до:

\[ E_{photon} = E_{electron}+E_{positron}\]

\[ 3 = E_{electron}+E_{positron}\]

і\(y\) -збереження імпульсу (ігнорування ядра знову):

\[ 0 = -pc_{electron} + pc_{positron}\]

\[ pc_{electron} = pc_{positron}\]

Так як пари мають рівні моменти, вони повинні мати рівну енергію, так що:
\[ 3 =2E_{either}\]

\[E_{either} - 1.5 \text{ MeV}\]

\[KE_{either} = (1.5-0.511)\text{ MeV}\]

\[KE_{either} 0.989\text{ MeV}\]

Для того, щоб x-імпульс був збережений,
\[pc_{photon} = pc_{nucleus}\]

\[3\text{ MeV} = pc_{nucleus}\]

Використовуючи\(E_{total}^2 =(pc)^2 +(mc^2)^2\) і відзначаючи, що атомна маса атома свинцю\(207.2 \text{ u} = 193007 \text{ MeV}\) дає,
\[E_{nucleus}=\sqrt{3^2+193007^2}\]

\[E_{nucleus}=193007\text{ MeV} \sqrt{1+\frac{9}{193007^2}}\]
потім спростити використання біноміального розширення,
\[E_{nucleus}=193007\text{ MeV} \bigg(1+\frac{1}{2}\frac{9}{193007^2}\bigg)\]

\[E_{nucleus}=193007\text{ MeV} (1+1.2\times10^{-10})\]

\[E_{nucleus}=193007\text{ MeV} + 2.33\times10^{-5} \text{ MeV}\]

\[KE_{nucleus} = 2.33 \times 10^{-5} \text{ MeV}\]

\[KE_{nucleus} =23.3\text{ eV}\]

Таким чином, ядро може зберегти збереження імпульсу, лише «вкравши» смішно малу частину загальної доступної енергії. Таким чином, ми можемо ігнорувати присутність ядра при поділі енергії вхідного фотона між електроном і позитроном.