4.2: Комптонне розсіювання
- Page ID
- 79213
Комптонним розсіянням називають розсіювання світла від вільних електронів. Експериментальним шляхом створити ціль з абсолютно вільних електронів неможливо. Однак якщо падаючі фотони мають енергію набагато більшу, ніж типові енергії зв'язування електронів з атомами, електрони будуть «збиватися» з атомів фотонами і виступати вільними частинками. Тому розсіювання Комптона зазвичай відноситься до розсіювання фотонів високої енергії від атомних цілей.
Якби світло було чисто хвильовим явищем, вхідна хвиля з певною частотою призвела б до коливання електрона з тією ж частотою. Коливальний електрон тоді випромінював електромагнітні хвилі цієї частоти. Таким чином, розсіяне світло і вхідне світло мали б, щоб в межах незначних змін через ефект Доплера для світла, однакову частоту. Це не те, що видно експериментально.
Натомість уявімо світло потоком фотонів і проаналізуємо зіткнення фотона і електрона шляхом збереження енергії та імпульсу. Розглянемо падаючий фотон довжини хвилі, що\(\lambda\) вражає нерухомий електрон. Фотон розсіює на кут\(\theta'\) (і нову довжину хвилі\(\lambda'\)) і електрон до кута\(\phi\).
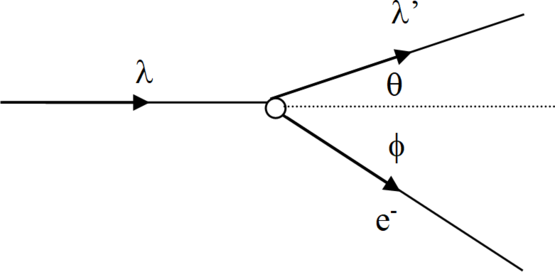
Для аналізу застосовують енергозбереження:
\[ E + mc^2 = E' + E_e\]
\(x\)-збереження імпульсу:
\[ pc + 0 = p'c \cos \theta + p_e c \cos \phi\]
і\(y\) -збереження імпульсу:
\[ 0 + 0 = p'c \sin \theta + p_e c \sin \phi\]
Для фотонів\(E = pc\), так рівняння імпульсу можна записати як:
\[ p_x: E = E' \cos \theta + p_e \cos \phi\]
\[ p_x: 0 = E' \cos \theta - p_e \sin \phi\]
Експериментально легше виявити розсіяний фотон, ніж розсіяний електрон, тому ми усунемо параметри електронів і виведемо взаємозв'язок між різними параметрами фотонів. Щоб усунути\(\phi\), вирішіть\(x\) -momentum і\(y\) -momentum for\(\cos \phi\) and\(\sin \phi\), а потім квадрат і складіть їх разом:
Розв'яжіть рівняння енергозбереження для\(E_e\):
\[ E_e = E + mc^2 - E'\]
\[E_e^2 = ( E + mc^2 -E')^2 \label{eq20}\]
Підключіть два попередні результати до Equation\ ref {eq20}, щоб усунути електронні змінні:
\[E_e^2 = (p_ec)^2 + (mc^2)^2\]
\[ ( E + mc^2 -E')^2 = E^2 - 2EE' \cos \theta E'^2 + (mc^2)^2\]
Шість термінів скасовують і рівняння значно спрощує
\[ 2Emc^2 - 2E'mc^2 - 2EE' = -2EE' \cos \theta\]
Перестановка дає
Цей результат безпосередньо пов'язує вхідну довжину хвилі з розсіяною довжиною хвилі та кутом розсіювання. Всі ці параметри легко вимірюються експериментальним шляхом. За своє теоретичне пояснення і експериментальну перевірку високоенергетичного розсіювання фотонів американець Артур Комптон був удостоєний Нобелівської премії в 1927 році.
Використання співвідношення розсіяння Комптона
Фотон 800 кеВ стикається з електроном в спокої. Після зіткнення фотон виявляється з 650 кеВ енергії. Знайдіть кінетичну енергію і кут розсіяного електрона.
Фундаментальним співвідношенням для розсіяння Комптона є
\[ \lambda' - \lambda = \dfrac{hc}{mc^2}( 1- \cos \theta)\]
де
- \(\lambda'\)це хвиля розсіяного фотона,
- \(\lambda \)хвиля падаючого фотона,
- і\(\theta \) є кутом розсіяного фотона.
Для знаходження кінетичної енергії розсіяного електрона не потрібно використовувати формулу Комптона. Якщо фотон спочатку має\(800\, \text{keV}\), а після розсіювання має\(650 \text{keV}\), то\(150, \text{keV}\) повинен був бути перенесений на електрон. Таким чином,\(KE_{electron} = 150 \text{keV}\).
Знаходження кута розсіяного електрона передбачає співвідношення Комптона. По-перше, перетворіть енергії фотонів в довжини хвиль:
\[ \begin{align} E_{photon} &= \frac{hc}{\lambda} \\[5pt] \lambda &= \frac{hc}{E} \\[5pt] &= \frac{1240 \text{ eVnm}}{800 \text{ keV}} = 1.55 \times 10^{-3} \text{ nm} \\[5pt] & = \frac{1240 \text{ eVnm}}{650 \text{ keV}} = 1.91 \times 10^{-3} \text{ nm} \end{align}\]
потім скористайтеся відносинами
\[ \lambda' - \lambda = \frac{hc}{mc^2}(1-\cos\theta)\]
\[1.91\times 10^{-3} - 1.55 \times 10^{-3} = \lambda = \frac{1240 \text{ eVnm}}{511 \text{ keV}}(1-\cos\theta)\]
\[0.1484 = (1-\cos\theta)\]
\[\theta = 31.6°\]
Однак це кут розсіювання фотона, а не електрона!
Щоб знайти кут розсіювання електрона, застосуйте збереження імпульсу в напрямку, перпендикулярному початковому напрямку фотонів.
\[0 = p_{\text{scattered photon}}c(\sin\theta)-p_{electron}c(\sin\phi)\]
\[ p_{\text{scattered photon}}c(\sin\theta) =p_{electron}c(\sin\phi)\]
\[E_{\text{scattered photon}}c(\sin\theta) = \sqrt{E_{electron}^2-(mc^2)^2}(\sin\theta)\]
\[650\sin(31.6)=\sqrt{(511+150)^2-(511)^2}(\sin\phi)\]
\[\sin\phi =0.813\]
\[\phi = 54.4\]
