13,4: Подвійна щілина

Подвійна щілина Фейнмана

Тут ми обговорюємо один з двох основних парадоксів, які ми використовуємо для впровадження квантової механіки. Це експеримент з подвійною щілиною для куль, водяних хвиль та електронів. Хоча багато людей експериментували з системами, про які слід обговорювати і писати про них, лікування Річарда Фейнмана настільки зрозуміле, що фізики часто називають його подвійною щілиною «Фейнмана». Наприкінці наведено 2 посилання, щоб ви могли прочитати «майстра» на цю тему.

Якщо ви читаєте цей документ он-лайн, є пара посилань на Flash-анімацію. Для їх перегляду потрібен Flash плеєр, який безкоштовний і доступний за адресою http://www.macromedia.com/.

Операційні визначення для «частинок» та «хвиль»

«Оперативне визначення» - це лише чітко визначена повторювана експериментальна процедура, результат якої визначає слово або слова. Наприклад, можна проводити широкі обговорення значення слова інтелект. Оперативне визначення розвідки, яке стоїть на стороні цих дискусій, може бути:

Я призначаю людині тест на IQ Стенфорда-Біне і оцінюю результат. Інтелект людини - це оцінка на тесті.

Тут ми будуємо оперативні визначення слів «частинки» і «хвилі».

Спочатку обговоримо «частинки» і візьмемо в якості нашого прототипу кулі з кулемета. У нас є кулемет, шматок бронепластини, в якому вирізані дві невеликі щілини, позначені «1» і «2», детектор і суцільний бронепластинчастий задній упор. Детектор досить простий: це балончик, в який ми помістили трохи піску. Повернемо навідника вільно на, скажімо, на 1 хвилину лопнув, а потім подивимося, скільки куль прибуде в банку. Спорожнюємо банку, а потім переміщаємо її в інше положення на задній зупинці, розкручуємо навідника ще на 1 хвилину лопнув, і дивимося, скільки куль прибуло на нову позицію. Повторюючи процедуру, ми можемо визначити розподіл куль, що надходять в різні положення на задньому стопі.

Виявляється кулеметник п'яний, так що він розпорошує кулі хаотично на всі боки.

Апарат зображений праворуч. Ми зробимо три різних «експерименту» з цим апаратом.
Спочатку закриваємо нижню щілину і вимірюємо розподіл куль, що надходять на задній упор з верхньої щілини. Для деяких розмірів куль і ширини щілини, хоча багато куль будуть йти прямо через щілину значна частка буде рикошет від броні пластини. Таким чином, розподіл куль виглядає так, як показано кривою праворуч.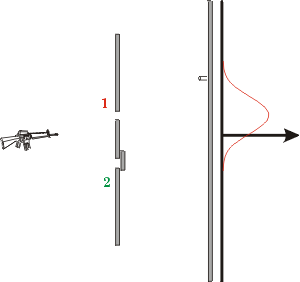
Далі закриваємо верхню щілину, і вимірюємо розподіл куль, що надходять на задній упор з нижньої щілини. Форма, показана у вигляді кривої праворуч, така ж, як і попередня, але зрушена вниз.
Нарешті, ми залишаємо обидві щілини відкритими і вимірюємо розподіл куль, що надходять на задній упор з обох щілин. Результатом є суцільна крива, показана праворуч. Також показані пунктирними лініями результати, які ми щойно отримали для куль з верхньої щілини та куль з нижньої щілини.

Результат - саме те, що ви, мабуть, передбачили: кількість куль, що надходять з обох щілин, - це лише сума куль з верхньої щілини та куль з нижньої щілини.

Пізніше буде корисно зрозуміти, що оскільки шлях однієї кулі є випадковим, розподіли, які ми вимірювали вище, по суті вимірюють ймовірність того, що дана куля прийде в певне положення на задній зупинці.

Тепер звернемо свою увагу на хвилі. У мого вчителя фізики середньої школи був пристрій під назвою «пульсаційний танк», який є лише резервуаром з оргскла, який можна було заповнити водою. Різні пристрої будуть натискати поверхню води, викликаючи поширення водних хвиль з пристрою. Можна вставляти щілини та інші об'єкти на шляху хвиль. Весь апарат був встановлений на проекторі, тому його можна було використовувати в якості демонстрації класу. Мій вчитель абсолютно любив свій пульсаційний танк, тому клас фізики був в основному водною грою. Я не знаю, чому він був так закоханий пристроєм або що він очікував, що ми дізнаємося від нього, але до цього дня, коли я думаю про прототип хвилі, я думаю про водні хвилі в пульсаційному резервуарі. Тож ми повторимо експерименти з подвійною щілиною, які ми щойно зробили в пульсаційному резервуарі.

Спочатку показуємо апарат. Справа в тому, що постукує по поверхні води - це маленький чорний гурток посередині всіх концентричних кіл. Концентричні кола - це водні хвилі, що поширюються подалі від джерела. Так само, як і раніше, у нас є дві щілини і зворотна зупинка. Якраз перед задньою зупинкою знаходиться наш «детектор», який є всього лише пробкою, плаваючою на поверхні води. Ми вимірюємо, скільки пробка пробивається вгору і вниз і визначаємо кількість енергії хвилі, що надходить в це положення на задній зупинці. Переміщення пробки в інші положення дозволить нам визначити розподіл хвильової енергії на задній зупинці.
Тепер закриваємо нижню щілину, і вимірюємо розподіл енергії хвилі, що надходить на задній упор якраз з верхньої щілини. Для деяких комбінацій ширини щілини і довжини хвилі буде спостерігатися значне поширення хвилі після її проходження через щілину. Якщо ви коли-небудь спостерігали прибій, що надходить через відносно невелику щілину в морській стінці, ви, можливо, спостерігали це. Розподіл показаний кривою вправо. Відзначимо, що він дуже схожий на розподіл куль з однієї щілини.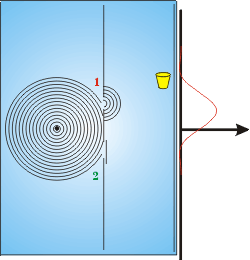
Тепер закриваємо верхню щілину і вимірюємо розподіл хвильової енергії, що надходить з нижньої щілини, як показано праворуч.
Нарешті, залишаємо обидві щілини відкритими і вимірюємо розподіл. Результат показаний праворуч. Як ми робили для куль, пунктирні лінії показують результати, які ми щойно отримали для розподілу лише з верхньої та нижньої щілин, тоді як суцільна лінія є результатом для обох розрізів, відкритих. Це виглядає не що інше, як результат для куль. Є місця, де загальна енергія хвилі набагато більше суми з двох щілин, і інші місця, де енергія майже дорівнює нулю. Такий розподіл називається інтерференційною схемою.

На цьому «оперативне визначення», яке нам потрібно визначити хвилі і частинки. У експерименті з двома щілинами частинка не показує інтерференційної картини, і ймовірність того, що частинка прибуває в місце на задній зупинці з відкритими обома щілинами, є лише сумою ймовірності її прибуття через верхню щілину плюс ймовірність її прибуття через нижню щілина. Хвиля показує інтерференційну картину.

Якщо ви думаєте про збереження енергії, ви можете трохи потурбуватися про інтерференційну картину для хвиль. Немає жодної проблеми. Загальна енергія в інтерференційній картині дорівнює енергії, що надходить з верхньої щілини плюс енергія, що надходить з нижньої щілини: інтерференційна картина повторно організовує енергію, але зберігає загальну кількість енергії.

Ми можемо пояснити інтерференційну картину для хвиль. Коли дві хвилі з двох щілин прибудуть в деяке положення на задній зупинці, за винятком праворуч посередині, вони пройшли різні відстані від щілин. Це означає, що їх «завивка» може не синхронізуватися.

На малюнку праворуч показано дві хвилі, повністю «поза фазою» один з одним. Їх сума завжди дорівнює нулю. Це в основному те, що відбувається на мінімумах інтерференційної картини.
На малюнку праворуч показані дві хвилі в фазі. Загальна хвиля - це сума двох. Це те, що відбувається на максимумах в інтерференційній картині.

Експеримент з двома щілинами для світла

У Стародавній Греції існували суперечки про природу світла. Евклід, Птолемей та інші вважали, що «світло» - це якийсь промінь, який рухається від ока до спостережуваного об'єкта. Атомісти і Аристотель припускали зворотне. Майже через 800 років після того, як Птолемей, близько 965 р. н.е., в Басрі в нинішньому Іраку, Абу Алі аль-Хасан ібн аль-Хайтам (Альхазен) вирішив суперечку розумним аргументом. Він сказав, що якщо довго дивитися на Сонце, ви будете горіти очі: це можливо тільки в тому випадку, якщо світло йде від Сонця до наших очей, а не навпаки.

У 1672 році вибухнула інша суперечка щодо природи світла: Ньютон стверджував, що світло - це якась частинка, так що світло від сонця досягає землі, тому що ці частинки можуть подорожувати через вакуум. Гук і Гюйгенс стверджували, що світло - це якась хвиля. У 1801 році Томас Янг поставив справу на експериментальне випробування, зробивши експеримент з подвійною щілиною для світла. В результаті вийшла інтерференційна картина. Таким чином, Ньютон помилився: світло - це хвиля. На малюнку показаний фактичний результат експерименту з подвійною щілиною для світла.

Звичайно, ми нічого не сказали про те, що таке «махає» або в якому середовищі він махає. Але, з точки зору нашого оперативного визначення зрозуміло, що світло - це хвиля чогось.

Електронні гармати

Електронна гармата, наприклад, в телевізійній картинній трубці, генерує пучок електронів. У цьому розділі ми обговоримо, як це працює. Ці деталі не важливі для нашої основної мети тут, тому ви можете перейти до наступного розділу, натиснувши тут.

Справа з'являється діаграма електронної гармати. Є дві вертикальні металеві пластини; права пластина має невеликий отвір, вирізаний в ній. Джерело напруги, позначене V, підтримує напругу на пластин, при цьому ліва пластина негативна, а права пластина позитивна. Коли металева пластина нагрівається, процес, званий термоіонним випромінюванням, буквально кипить електрони з поверхні металу. Зазвичай електрони роблять його лише на частку міліметра; це тому, що коли електрон википів від поверхні металу, він залишив ту частину пластини з чистим позитивним електричним зарядом, який тягне електрон прямо назад у пластину.

На малюнку ми нагріваємо ліву пластину, щоб термоелектронні електрони википали з поверхні. Але через різницю напруги підтримується по всій пластині, електрони, які википають між двома пластинами, не потрапляють назад в пластину, а замість цього притягуються до позитивної пластини правої руки. Більшість електронів врізаються в позитивну пластину, як показано на малюнку. Однак електрон посередині врізався б у пластину, за винятком того, що ми прорізали отвір у цій її частині. Таким чином, ми отримуємо пучок електронів з цієї «електронної гармати».

У справжніх електронних гарматах, таких як на задній панелі телевізійної трубки, негативна пластина не нагрівається багаттям, як на нашому малюнку. Замість цього невелика нитка дроту має струм, що пройшов через неї. Нитка розжарювання нагрівається, світиться червоним кольором і нагріває негативну пластину. Можливо, ви бачили, що червоне світіння в задній частині телевізійної трубки.

Ми контролюємо швидкість електронів в пучку з напругою, а кількість електронів тим, наскільки гарячою ми робимо негативно заряджену пластину.

Ще один невеликий момент. Оскільки отвір у правій пластині не має нульового розміру, електрони можуть з'являтися в напрямках, трохи віддалених від ідеально горизонтальної. Таким чином, промінь електронів буде прагнути кілька «розпорошити».

Відтепер ми помістимо електронну гармату в чорну скриньку і представляємо електронний промінь, що йде від неї, як показано праворуч.

Експеримент з двома щілинами для електронів

У попередньому розділі ми обговорювали, як виробляти пучок електронів з електронної гармати. Тут ми поміщаємо електронну гармату всередину скляної трубки, в якій було відкачано все повітря. Правий скляний екран має внутрішню частину, покриту люмінофором, який буде виробляти невеликий сплеск світла, коли електрон вдарить по ньому. Наприклад, у телевізійній трубці зображення поля направляють промінь електронів у потрібне місце, інтенсивність електронів змінюється залежно від того, де ми керуємо променем, і наш розум та/або очі інтерпретують спалахи як зображення, яке ми бачимо на телебаченні.

Нерухомість	Значення
Маса	9,11 × 10 ^-31 кг
Електричний заряд	1,60 × ^10-19 кулонів
Спін кутовий імпульс	5,28 × 10 ^-35 Джоуль-секунд

Тепер «всі знають», що електрони - це частинки. Вони мають чітко визначену масу, електричний заряд і т.д. деякі з цих властивостей перераховані праворуч. Хвилі не мають чітко визначених мас і т.д.

Коли електрон залишає електронну гармату, через частку секунди на екрані з'являється спалах світла, який вказує, де він приземлився. Хвиля поводиться по-іншому: коли хвиля залишає джерело, вона поширюється, розподіляючи свою енергію за схемою, як обговорювалося на початку цього документа.

За винятком того, коли ми розміщуємо дві щілини на шляху електронів, як показано, на екрані ми бачимо інтерференційну картину! Насправді те, що ми бачимо на екрані, виглядає ідентично малюнку перешкод з подвійною щілиною для світла, яку ми бачили раніше.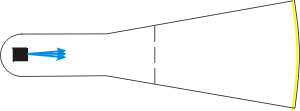

Якщо це здається дуже загадковим, ви не самотні. Розуміння того, що тут відбувається, в певному сенсі еквівалентно розумінню квантової механіки. Я не розумію квантової механіки. Фейнман зізнався, що ніколи не розумів квантову механіку. Це може бути правдою, що ніхто не може зрозуміти квантову механіку в звичайному значенні слова «зрозуміти».

Зараз ми будемо розширювати наше розуміння нашого нерозуміння. Одна з можливостей щодо витоків інтерференційної картини полягає в тому, що електрони, що проходять через верхню щілину, якимось чином взаємодіють з електронами, що проходять через нижню щілину. Зауважимо, що ми поняття не маємо, яким може бути такий механізм, але трохи відчайдушно хочемо зрозуміти, що тут відбувається. Ми можемо дослідити цю ідею, уповільнивши швидкість електронів з гармати так, що в системі знаходиться лише один електрон. Що ми робимо - це вогонь електрона, бачимо, де спалах світла відбувається на екрані люмінофора, почекаємо деякий час, поки все осяде, потім запускаємо інший електрон, відзначаючи, де він приземляється на екрані.

Після того, як ми випустили велику кількість електронів, ми виявимо, що розподіл електронів все ще є інтерференційною схемою.

Я підготував невелику Flash-анімацію, яка імітує цей результат. Ви можете отримати доступ до анімації, натиснувши на червону кнопку праворуч. Розмір файлу становить 6.4k. Ви можете отримати Flash-плеєр безкоштовно з http://www.macromedia.com/; наша анімація призначена для версії 5 або пізнішої версії плеєра.

Ви можете знати, що в анімації положення електрона генерується випадковим чином за допомогою методу Монте-Карло. Таким чином, якщо ви «Перемотати» анімацію, щоб почати її спочатку, то нарощування гістограми майже напевно не буде ідентичним попередньому «пробному».

Ми робимо висновок, що все, що відбувається, щоб викликати інтерференційну картину, не включає два або більше електронів, що взаємодіють один з одним. І все ж, з одним електроном одночасно в системі, з відкритими обома щілинами є місця на екрані, куди електрони не йдуть, хоча з відкритою лише однією щілиною деякі електрони виявляються в такому положенні.

Тепер, щоб отримати інтерференційний малюнок, беремо хвилю, розбиваємо її на дві частини, направляємо кожну частину через одну з щілин, а потім рекомбінуємо хвилі. Чи означає це, що один електрон якось проходить через обидві щілини відразу? Це теж піддається експериментальному випробуванню.

Результат виконання тесту виявляється незалежним від деталей того, як проводиться експеримент, тому уявімо дуже просте розташування: поміщаємо лампочку за щілинами і дивимося, що відбувається. Зверніть увагу, що в реальному експерименті лампочка повинна була б бути менше, ніж на малюнку, і щільніше заправлена за щілинами, щоб електрони не стикалися з нею.

Ми побачимо невеликий спалах світла, коли електрон проходить через щілини.

Ми бачимо, що кожен електрон діє цілком «нормально»: половина електронів проходить через верхню щілину, одна половина проходить через нижню щілину, і що буде для даного електрона, здається випадковим. Тут можна побачити невелику (24k) gif анімацію того, що ми могли б побачити в цьому експерименті.

Але тим часом у нас є колега, який спостерігає за спалахами світла на екрані, покритому люмінофором, який каже: «Гей, інтерференційна картина щойно пішла!» І насправді розподіл електронів на екрані тепер точно такий же, як і розподіл кулеметних куль, які ми бачили вище. Цифра праворуч - це те, що бачить наш колега на екрані.

Очевидно, що коли ми дивимося на те, що відбувається на щілині, ми викликаємо якісну і незворотну зміну поведінки електронів. Зазвичай це називається «Принцип невизначеності Гейзенберга».

Всі завжди знали, що проведення будь-яких вимірювань на будь-якій системі викликає порушення в системі. Класична парадигма полягала в тому, що принаймні в принципі порушення можна мінімізувати до того, що воно незначне.

Чи можна мінімізувати порушення, що викликаються лампочкою? Ми можемо зменшити інтенсивність світла, яке він випромінює. Однак, якщо ми спробуємо це, саме в той момент, коли світло стає настільки слабким, що нам не вистачає деяких електронів, інтерференційна картина починає повертатися! Насправді, якщо інтенсивність світла, скажімо, така, що нам не вистачає половини електронів, ми маємо половину інтерференційної картини і половину розподілу частинок. Тож ця спроба мінімізувати порушення не спрацювала: ми досі не знаємо, що відбувається на щілині, коли бачимо інтерференційну картину.

Є ще один спосіб мінімізувати порушення. Світло містить енергію, і виходить, що якщо ми збільшимо довжину хвилі світла, у напрямку до інфрачервоного випромінювання, енергія кожної частини світла йде вниз. Можливо, якщо ми зменшимо енергію у світлі, ми не будемо так сильно розсіювати її від електронів. Отже, починаємо збільшувати довжину хвилі світла, що випромінюється лампочкою. Ми продовжуємо бачити всі електрони, і спочатку ми завжди бачимо, що половина з них проходить через верхню щілину, а половина - через нижню щілину.

Однак наша здатність вирішувати дві позиції в просторі, дивлячись залежить від довжини хвилі світла, з яким ми бачимо. І саме в той момент, коли довжина хвилі світла від лампочки стає настільки великою, що, хоча ми бачимо електрони, ми не можемо сказати, через яку щілину вони пройшли, інтерференційна картина повертається назад.

Один студент одного разу зауважив, що ми повинні зробити «кращий» експеримент. Принцип невизначеності Гейзенберга говорить, що такого кращого експерименту не існує. Зокрема, Ейнштейн присвятив багато часу, намагаючись розробити такий кращий вимір; всі його спроби зазнали невдачі.

Висновок всього цього полягає в тому, що не існує експерименту, який міг би сказати нам, що роблять електрони в щілині, які також не руйнують інтерференційну картину. Це, здається, означає, що немає відповіді на питання про те, що відбувається в щілині, коли ми бачимо інтерференційну картину. Шляхи електрона від електронної гармати до екрану непізнавані, коли ми бачимо інтерференційну картину. Як сказав Гейзенберг, «шлях [електрона] з'являється тільки тоді, коли ми його спостерігаємо».

Ми будемо обговорювати тлумачення того, що все це може означати, дуже докладно пізніше. Поки я коротко згадаю «стандартне», якщо неповне тлумачення. Якщо ми думаємо, що ймовірність того, де електрон знаходиться в просторі, - це хвиля, то, коли ми не дивимося, хвиля ймовірності має дві частини на щілині, що представляє собою той факт, що є 50% шанс, що електрон пройшов через верхню щілину і 50% шанс, що він пройшов через нижню щілину. Ці дві хвилі ймовірності з двох щілин, потім, рекомбінуються на екрані і викликають інтерференційну картину.

Коли ми дивимося, ми «руйнуємо державу» зі 100% шансом, що вона пройшла через одну щілину і 0% шанс, що вона пройшла через іншу. І в цій обставині дві хвилі ймовірності для двох щілин не можуть потім рекомбінувати на екрані, щоб викликати інтерференційну картину: для кожного електрона існує лише одна ненульова хвиля ймовірності.

Нарешті, ми маємо дві суперечливі, але взаємодоповнюючі моделі двощілинного експерименту для електронів. В одній моделі електрон - це частинка, яка так чи інакше проявляє інтерференційну картину. В іншій моделі електрон - це хвиля, яка якось проявляється як частинка, коли ми дивимося на неї.

Flash-анімацію цих двох моделей, обидві неповні, можна отримати, натиснувши червону кнопку праворуч. Розмір файлу становить 23k і з'явиться в окремому вікні.

Посилання

• Річард Фейнман, Характер фізичного права (MIT, 1965), глава 6
• Річард Фейнман, Роберт Лейтон і Метью Сендс, Лекції Фейнмана з фізики (Аддісон-Веслі, 1963), Том III, Глава 1