13.1: Теорема Белла
- Page ID
- 77181
ВСТУП
У 1975 році Стапп назвав теорему Белла «найглибшим відкриттям науки». Зауважимо, що він говорить наука, а не фізика. Я з ним згоден.
У цьому документі ми вивчимо теорему. Припускаємо деяке знайомство з поняттям хвильово-частинкової подвійності. Ми також припускаємо значне знайомство з експериментом Штерна-Герлаха та концепцією кореляційного експерименту.
Підготовлено набагато простіший вступ до теореми з деякою втратою повноти. Ви можете отримати доступ до html або pdf версії з посиланнями праворуч.
Витоками цієї теми є знаменита стаття Ейнштейна, Розена та Подільського (ЕПР) 1935 року; її назва - Чи можна вважати квантово-механічним описом фізичної реальності завершеним? Вони розглянули те, що Ейнштейн назвав «моторошним дією на відстані», яке, здається, є частиною квантової механіки, і дійшли висновку, що теорія повинна бути неповною, якщо не зовсім неправильною. Як ви, напевно, вже знаєте, Ейнштейн ніколи не приймав квантову механіку. Одне з його заперечень полягало в тому, що «Бог не грає в кістки зі Всесвітом». Бор відповів: «Киньте говорити Богу, що робити!»
На початку 1950-х Девід Бом (не «Бор») був молодим професором фізики в Прінстонському університеті. Йому було доручено викладати квантову механіку і, як це прийнято, вирішив написати підручник на цю тему; книга досі є класикою. Ейнштейн був у Прінстоні в цей час, і коли Бом закінчив кожну главу книги, Ейнштейн критикував би її. До того часу, як Бом закінчив книгу Ейнштейн переконав його, що квантова механіка принаймні неповна. Потім Бом провів багато років у пошуках прихованих змінних, неспостережуваних факторів всередині, скажімо, радіоактивного атома, який визначає, коли він збирається розпастися. У теорії прихованих змінних час розпаду не є випадковим, хоча змінна, яка контролює процес, прихована від нас. Ми детально обговоримо роботу Бома пізніше в цьому документі.
У 1964 році Дж.С. Белл опублікував свою теорему. Він був відлитий з точки зору прихованої теорії змінних. З тих пір з'явилися інші докази d'Espagnat, Stapp та інші, які не є з точки зору прихованих змінних. Нижче ми зробимо варіацію на доказ d'Espagnat, який я розробив; спочатку він був опублікований в Американському журналі фізики 50, 811 - 816 (1982).
ДОВЕДЕННЯ НЕРІВНОСТІ БЕЛЛА
Будемо трохи математичними. Деталі математики не важливі, але є кілька частин доказів, які будуть важливими. Результатом доказування буде те, що для будь-якої колекції об'єктів з трьома різними параметрами, A, B і C:
Кількість об'єктів, які мають параметр A, але не параметр B плюс кількість об'єктів, які мають параметр B, але не параметр C, більше або дорівнює кількості об'єктів, які мають параметр A, але не параметр C.
Ми можемо написати це більш компактно, як:
Число (A, а не B) + Число (B, а не C) більше або дорівнює числу (A, а не C)
Відносини називають нерівністю Белла.
У класі я часто роблю учням колекцію предметів і вибираю параметри, які повинні бути:
A: чоловік B: зріст понад 5' 8" (173 см) C: блакитні очі
Тоді нерівність стає, що кількість чоловіків студентів, які не мають висоти понад 5' 8" плюс кількість студентів, чоловіків і жінок, з висотою понад 5' 8", але які не мають блакитних очей більше або дорівнює кількості чоловіків студентів, які не мають блакитних очей. Я абсолютно гарантую, що для будь-якої колекції людей це виявиться правдою.
Важливо підкреслити, що ми не робимо жодного статистичного припущення: клас може бути великим, малим або навіть нульовим розміром. Крім того, ми не припускаємо, що параметри є незалежними: зверніть увагу, що існує тенденція співвідношення між статтю та зростом.
Іноді люди мають проблеми з теоремою, тому що ми будемо робити варіацію техніки, яка називається доказом заперечення. Наприклад, ось силогізм:
Всі павуки мають шість ніг. Всі шість ногих істот мають крила. Тому у всіх павуків є крила.
Якщо ми коли-небудь спостерігаємо павука, який не має крил, то ми знаємо, що принаймні одне і, можливо, обидва припущення силогізму невірні. Аналогічно, ми виведемо нерівність, а потім покажемо експериментальну обставину, де вона не відповідає дійсності. Таким чином, ми будемо знати, що принаймні одне з припущень, яке ми використовували при виведенні, є неправильним.
Також ми побачимо, що доказ та його експериментальні тести не мають абсолютно нічого спільного з квантовою механікою.
Тепер ми готові до самого доказу. По-перше, я стверджую, що:
Число (A, а не B, C) + Число (не A, B, не C) має бути або 0, або натуральне число
або еквівалентно:
Число (A, а не B, C) + Число (не A, B, не C) більше або дорівнює 0
Це має бути досить очевидним, оскільки або жодні члени групи не мають цих комбінацій властивостей, або деякі члени.
Тепер ми додаємо число (A, а не B, не C) + Число (A, B, а не C) до вищевказаного виразу. Ліва сторона:
Число (A, а не B, C) + Число (A, а не B, не C) + Число (не A, B, не C) + Число (A, B, не C)
а права сторона - це:
0 + Число (A, а не B, не C) + Число (A, B, а не C)
Але ця права сторона якраз:
Число (A, а не C)
оскільки для всіх членів або B, або не B має бути істинним. У наведеному вище прикладі класу, коли ми підраховували кількість чоловіків без блакитних очей, ми включаємо як тих, чий зріст був більше 5 футів 8 «, так і тих, чий зріст не перевищував 5 футів 8».
Вище ми писали «оскільки для всіх членів або B, або не B повинні бути істинними». Це виявиться важливим.
Ми можемо аналогічно зібрати терміни і написати ліву частину як:
Число (A, а не B) + Число (B, а не C)
Оскільки ми почали доказ, стверджуючи, що ліва сторона більше або дорівнює правій стороні, ми довели нерівність, яку я повторюю:
Число (A, а не B) + Число (B, а не C) більше або дорівнює числу (A, а не C)
Ми зробили два припущення на доказ. Це:
- Логіка - це вагомий спосіб розуму. Весь доказ - це вправа на логіку, приблизно на рівні загадок «Веселощі з цифрами» іноді можна побачити в газетах і журналах.
- Параметри існують незалежно від того, вимірюються вони чи ні. Наприклад, коли ми зібрали терміни Number (A, not B, not C) + Число (A, B, not C), щоб отримати Число (A, а не C), ми припускали, що або не B, або B вірно для кожного члена.
ЗАСТОСУВАННЯ НЕРІВНОСТІ БЕЛЛА ДО ЕЛЕКТРОННОГО СПІНА
Розглянемо пучок електронів з електронної гармати. Виставимо наступні призначення для трьох параметрів нерівності Белла:
A: Електрони є «спін-вгору» для «вгору» визначається як прямий вгору, який ми будемо називати кутом нуль градусів. B: електрони «спін-ап» для орієнтації 45 градусів. C: електрони «спін-ап» для орієнтації 90 градусів.
Тоді нерівність Белла буде читати:
Число (спін-вгору нуль градусів, не спін-вгору 45 градусів) + число (спін-вгору 45 градусів, не спін-вгору 90 градусів) більше або дорівнює числу (спін-вгору нуль градусів, не спін-вгору 90 градусів)
Але розгляньте спробу виміряти, скажімо, число (A, а не B). Це кількість електронів, які обертаються на нуль градусів, але не обертаються на 45 градусів. Бути «не спін-вгору на 45 градусів» - це, звичайно, віджимання на 45 градусів.
Ми знаємо, що якщо ми виміряємо електрони з гармати, половина з них буде спін-вгору і одна половина буде спін-вниз для орієнтації 0 градусів, і що буде для окремого електрона випадково. Аналогічно, якщо виміряти електрони з фільтром, орієнтованим на 45 градусів, одна половина буде спін-вниз, а одна половина - спін-вгору.
Але якщо ми спробуємо виміряти віджимання як на 0 градусів, так і 45 градусів, у нас є проблема.
На малюнку праворуч показано вимірювання спочатку при 0 градусах, а потім при 45 градусах. З електронів, що виходять з першого фільтра, 85% пройдуть другий фільтр, а не 50%. Таким чином, для електронів, які вимірюються, щоб бути спін-вгору для 0 градусів, 15% спін-вниз для 45 градусів.
Таким чином, вимірювання спина електрона під кутом нуля градусів безповоротно змінює кількість електронів, які обертаються вниз для орієнтації 45 градусів. Якщо ми спочатку вимірюємо при 45 градусах, ми змінимо, чи це спін-вгору на нуль градусів. Аналогічно для інших двох термінів у цьому застосуванні нерівності. Це наслідок принципу невизначеності Гейзенберга. Таким чином, ця нерівність не експериментально перевіряється.
У нашому класному прикладі аналогія полягала б у тому, що визначення статі учнів змінило б їх зріст. Досить дивно, але вірно для вимірювання електронного спина.
Однак нагадаємо про кореляційні експерименти, про які ми говорили раніше. Уявіть, що електронні пари, які випромінюються радіоактивною речовиною, мають сумарний спін нуль. Під цим ми маємо на увазі, що якщо правий електрон обертається, його супутній електрон гарантовано буде спін-вниз за умови, що два фільтри мають однакову орієнтацію.
Скажімо, в ілюстрованому експерименті лівий фільтр орієнтований на 45 градусів, а права - на нуль градусів. Якщо лівий електрон проходить через його фільтр, то він віджимається на орієнтацію 45 градусів. Тому ми гарантуємо, що якби ми виміряли його супутній електрон, він би обертався для орієнтації 45 градусів. Ми одночасно вимірюємо правий електрон, щоб визначити, чи він розкручується на нуль градусів. І оскільки жодна інформація не може подорожувати швидше, ніж швидкість світла, вимірювання лівої руки не може порушити вимірювання правої руки.
Таким чином, ми «обіграли» Принцип невизначеності: ми визначили, чи електрон праворуч спін-вгору нульовий градус, а не спін-вгору 45 градусів, вимірюючи його спін при нульових градусах та спін супутника при 45 градусах.
Тепер ми можемо записати нерівність Белла як:
Число (правий спін-вгору нуль градусів, лівий спін-вгору 45 градусів) + число (правий спін-вгору 45 градусів, лівий спін-вгору 90 градусів) більше або дорівнює число (правий спін-вгору нуль градусів, лівий спін-вгору 90 градусів)
На цьому наше доказ теореми Белла завершено.
Ця ж теорема може бути застосована і до вимірювань поляризації світла, що еквівалентно вимірюванню спіна фотонних пар.
Експерименти були проведені. Для електронів лівий поляризатор встановлений на 45 градусів, а правий - на нуль градусів. Промінь, скажімо, мільярд електронів вимірюється для визначення числа (правий спін-вгору нуль градусів, лівий спін-вгору 45 градусів). Потім поляризатори встановлюються на 90 градусів/45 градусів, ще мільярд електронів вимірюються, потім поляризатори встановлюються на 90 градусів/нуль градусів для ще мільярда електронів.
Результатом експерименту є те, що нерівність порушується. Перший опублікований експеримент був Клаузер, Хорн, Шимоні і Холт в 1969 році з використанням фотонних пар. З тих пір експерименти повторювалися багато разів.
Експерименти, проведені до цих пір, були для пар електронів, протонів, фотонів та іонізованих атомів. Виявляється, робити експерименти на фотонних парах простіше, тому більшість тестів використовують саме їх. Таким чином, в більшій частині решти цього документа слово «електрон» є родовим.
Технічна примітка: Ви можете згадати з нашого обговорення експерименту Штерна-Герлаха, що проведення кореляційного експерименту для електронів з поляризаторами під деяким відносним кутом еквівалентно проведенню експерименту для фотонів з поляризаторами під половиною відносного кута електронних поляризаторів. Таким чином, коли ми обговорюємо вимірювання електронів з поляризаторами при, скажімо, нульових градусах і 45 градусах, для фотонного експерименту це буде нуль градусів і 22,5 градуси.
В останньому розділі ми зробили два припущення, щоб вивести нерівність Белла, які тут стають:
- Логіка діє.
- Електрони мають спін в заданому напрямку, навіть якщо ми не вимірюємо його.
Тепер ми додали третє припущення, щоб перемогти принцип невизначеності:
- Жодна інформація не може подорожувати швидше, ніж швидкість світла.
Ми заявимо про це трохи більш стисло, як:
- Логіка діє.
- Існує реальність, окрема від її спостереження.
- Населений пункт.
Ви згадаєте обговорювані нами докази запереченням. Той факт, що наша остаточна форма нерівності Белла експериментально порушена, вказує на те, що принаймні одне з трьох припущень, які ми зробили, виявилося неправильним.
Ви також нагадаєте, що раніше ми вказували, що теорема і її експериментальні тести не мають нічого спільного з квантовою механікою. Однак той факт, що квантова механіка правильно прогнозує кореляції, які спостерігаються експериментально, вказує на те, що теорія теж порушує хоча б одне з трьох припущень.
Нарешті, як ми вже заявляли, оригінальний доказ Белла був з точки зору прихованих теорій змінних. Його припущення були:
- Логіка діє.
- Приховані змінні існують.
- Приховані змінні є локальними.
Більшість людей, включаючи мене, розглядають припущення локальних прихованих змінних як дуже схоже на припущення про локальну реальність.
ЩО ЗАРАЗ?
Як можна легко уявити, багато людей намагалися вийти з цього глибокого результату. Деякі спроби критикували експериментальні тести. Один аргумент полягає в тому, що оскільки ми встановлюємо два поляризатори під деяким набором кутів, а потім збираємо дані для, скажімо, мільярда електронів, є достатньо часу, щоб поляризатори «знали» орієнтацію один одного, хоча і не будь-яким відомим механізмом. Більш пізні тести встановлюють орієнтацію поляризаторів випадковим чином після того, як електрони покинули джерело. Результати цих тестів такі ж, як і попередні експерименти: порушується нерівність Белла і підтверджуються прогнозовані квантові кореляції. Ще інші тести встановили відстань між двома поляризаторами на 11 км, результати знову підтверджують квантові кореляції.
Інша критика полягала в тому, що оскільки корельовані пари, що випромінюються джерелом, йдуть у всіх напрямках, лише дуже мала частина з них насправді в кінцевому підсумку вимірюється поляризаторами. Інший експеримент з використанням корельованих атомів берилію вимірював майже всі пари, при цьому результати знову підтвердили квантові кореляції.
Є ще одне заперечення проти експериментальних тестів, які, принаймні поки, ніхто не встиг повністю обійти. Ми вимірюємо спінову комбінацію, скажімо, нуль градусів і 45 градусів для колекції електронів, а потім вимірюємо іншу спінову комбінацію, скажімо, 45 градусів і 90 градусів, для іншої колекції електронів. У нашому прикладі в класі, це ніби як вимірювання кількості студентів чоловіків, зріст яких не перевищує 5' 8" в одному класі, а потім використовувати інший клас різних учнів, щоб виміряти кількість студентів, чий зріст перевищує 5' 8" але не мають блакитних очей. Різниця полягає в тому, що сукупність, скажімо, мільярда електронів від джерела в кореляційних експериментах завжди поводиться однаково в межах малих і очікуваних статистичних коливань при кожній іншій колекції мільярда електронів з джерела. Оскільки цей факт був перевірений багато разів для всіх експериментів усіх типів, ми припускаємо, що це правда, коли ми робимо ці кореляційні експерименти. Це припущення є прикладом індуктивної логіки; звичайно, ми припустили обґрунтованість логіки в нашій деривації.
Іноді можна побачити твердження про те, що теорема Белла говорить про те, що інформація передається зі швидкістю, більшою за швидкість світла. Поки я не бачив такого аргументу, який вважаю правильним. Якщо ми сидимо біля будь-якого з поляризаторів, ми бачимо, що половина електронів проходить, а половина - ні; що буде для окремого електрона, здається, випадковим. Таким чином, поведінка у нашого поляризатора не дозволяє нам отримати будь-яку інформацію про орієнтацію іншого поляризатора. Тільки в кореляції електронних спинив ми бачимо щось дивне. d'Espagnat використовує слово вплив для опису того, що може подорожувати з надсвітловими швидкостями.
Уявімо, ми беремо монетку і акуратно розпилюємо її навпіл так, щоб один шматок був «головою», а інший - «хвостами». Кожну половинку складаємо в окремий конверт і несемо в різні кімнати. Якщо ми відкриваємо один з конвертів і бачимо голови, ми знаємо, що інший конверт містить хвости. Цей кореляційний «експеримент» відповідає вимірюванням спина, коли обидва поляризатори мають однакову орієнтацію. Саме коли у нас поляризатори в різних орієнтаціях, ми бачимо щось дивне.
Поки що ми не знаємо, які з припущень, які ми зробили в доказі, є неправильними, тому ми вільні взяти наш вибір одного, двох або всіх трьох. Ми закриємо цей розділ, коротко розглянувши наслідки відкидання припущення про обґрунтованість логіки, а потім наслідки відкидання припущення про реальність окремо від її спостереження. У наступному розділі ми вивчимо ідею нелокального всесвіту.
Що робити, якщо логіка недійсна?
Ще задовго до Белла підозрювали, що квантова механіка конфліктує з класичною логікою. Наприклад, дедуктивна логіка заснована на ряді припущень, одним з яких є Принцип виключеної середини: всі твердження або істинні, або помилкові.
Але розглянемо наступне тестове питання з множинним вибором:
- Електрон - це хвиля.
- Електрон - це частинка.
- Все попереднє.
- Нічого з перерахованого вище.
З хвильово-частинкової подвійності ми знаємо, що обидва твердження 1 і 2 є як істинними, так і свого роду помилковими. Це, здається, ставить під сумнів Принцип виключеної середини. Таким чином, деякі люди працювали над багатозначною логікою, яка, як вони сподіваються, буде більш узгоджена з тестами теореми Беллса і, отже, з квантовою механікою. Гарі Зукава «Танцюючі майстри Ву Лі» добре обговорюють таку квантову логіку; оскільки існують численні видання цієї книги, і кожна глава нумерується 0, я не можу надати більш детальну довідку.
Саму математику можна розглядати як просто галузь дедуктивної логіки, тому, якщо ми переглянемо правила логіки, нам потрібно буде розробити нову математику
Можливо, вам буде цікаво дізнатися, що дедуктивна логіка довела, що логіка неповна. Доказ був опублікований в 1931 році Геделем; гарним посиланням є Гедель, Ешер, Бах Хофстадера. Ключем до роботи Геделя є самопосилання; ми побачимо приклад самопосилання в наступному підрозділі. Він довів, що будь-яка математика взагалі, якщо вона не обмежена тривіально, буде містити твердження, які не є ні правдивими, ні помилковими, а просто недоказованими.
| Під самопосиланням ми маємо на увазі твердження або сукупність тверджень, які посилаються на себе. Для прикладу розглянемо: Це твердження є помилковим. Зверніть увагу, що якщо це твердження істинно, то воно повинно бути помилковим. Якщо твердження if false, то воно повинно бути true. Отже, у нас є ланцюжок істинних» помилкових» істинних» помилкових... . |  Житель Нью-Йорка, 5 березня 2001 р., стор. 78. |
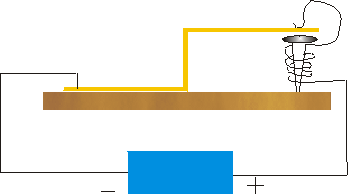Це може трохи нагадати вам простий зумер, наприклад дверний зумер.
Справа показаний зумер. Гнучкий шматок металу згинається в подвійну L форму і прибивається до дошки. Великий цвях кладуть якраз під праву частину металу, а метал підганяють так, щоб він не зовсім торкався великого нігтя. Акумулятор підключений таким чином, що коли метал L знаходиться в стані спокою, схема тільки завершується, що призводить до того, що великий цвях стає електромагнітом.
Це звичайно тягне метал вниз, що розриває ланцюг. Таким чином металеві пружини назад вгору, що завершує ланцюг знову, який тягне метал вниз і так далі. Таким чином, якщо ланцюг замкнутий, він розмикається, а якщо ланцюг розімкнутий, то вона замкнута. Або, ми говоримо, що у нас є ланцюг Закрито» Відкрито» Закрито» Відкрити... . Різниця між цим прикладом і попереднім самодовідковим твердженням полягає в тому, що тут коливання значення відбуваються в часі. Ви можете отримати доступ до Flash-анімації зумера, натиснувши тут.
Наприкінці дев'ятнадцятого століття логік Гільберт говорив: «Фізика занадто важлива, щоб її залишали фізикам». У помсту Дж.О. Уілер заявив: «Гедель занадто важливий, щоб його залишали математикам».
Нарешті, хоча дедуктивна логіка досить добре зрозуміла, нікому не вдалося кодифікувати залізні правила індуктивної логіки, які працюють послідовно. Міллс дуже намагався це зробити, але наступна історія Копі показує одну проблему:
«Улюбленим прикладом, яким користуються критики Методу згоди, є випадок Наукового п'є, який надзвичайно любив спиртні напої і напивався щовечора тижня. Він руйнував його здоров'я, і його нечисленні друзі, що залишилися, благали його зупинитися. Розуміючи себе, що не може йти далі, він вирішив провести ретельний експеримент, щоб виявити точну причину його частих сплутнень. П'ять ночей поспіль він збирав екземпляри даного явища, попередні обставини - відповідно скотч і газована вода, бурбон і газована вода, коньяк і газована вода, ром і газована вода, а також джин і сода [тьфу!]. Тоді, використовуючи Метод згоди, він присягнув урочистій клятві більше ніколи не чіпати газовану воду!»
Довідка: І.Копі, Вступ до логіки, 2-е видання, (Макміллан, Нью-Йорк, 1961), стор. 394-395.
Зверніть увагу на «приховану змінну» у наведеному вище матеріалі.
Що робити, якщо немає реальності окремо від її спостереження?
Як ми бачили, назва цього підрозділу дуже схожа на запитання, які наслідки відсутності прихованих змінних. Сконцентруємося на першій формі питання.
Можливо, ви вже помітили, що питання - це варіація старої філософської пилки щодо дерева, яке падає у лісі, де нікому не чути звуку.
Конфлікт між припущенням реальності та квантовою механікою підозрювався задовго до Белла. Наприклад, посилаючись на траєкторію руху електрона, скажімо, в експерименті з подвійною щілиною Гейзенберг заявив: «Шлях електрона з'являється тільки тоді, коли ми його спостерігаємо».
Людям давно відомо, що будь-яке вимірювання турбує вимірюється річ. Важливим припущенням класичних наук було те, що принаймні в принципі порушення можна зробити настільки малим, що ми можемо його ігнорувати. Таким чином, коли антрополог вивчає примітивну культуру на місцях, вона припускає, що її присутність в племені робить незначний вплив на поведінку членів. Іноді ми пізніше виявляємо, що все, що вона вимірювала, - це поведінка племені, коли за ним спостерігав антрополог.
Тим не менш, класично ми припускаємо модель, де ми, як спостерігачі, знаходимося за склом, де бачимо, що відбувається «там». Тепер ми припускаємо, що скло було розбито. Уілер пропонує нам повністю відмовитися від слова спостерігача і замінити його учасником.
Уілер більш глибоко замислювався над наслідками всесвіту участі, ніж будь-хто. Він придумав фігуру праворуч, підпис якої:
«Символічне зображення Всесвіту як самозбудженої системи, створеної за допомогою «самовідліку». Всесвіт народжує спілкуються учасників. Спілкуються учасники надають сенсу Всесвіту... З такою концепцією йде нескінченна серія відступаючих роздумів, які можна побачити в парі дзеркал, що стоять перед обличчям».
Довідка: Дж. Уілер в Ішамі та ін., Ред., Квантова гравітація (Кларендон, Оксфорд, 1975), стор. 564-565. Кольори були використані Уілером в колоквіумі в Департаменті фізики, Univ. Торонто кілька років тому.
Можливо, ви помітили подібність між цим поглядом квантової механіки та філософією ідеалістів єпископа Берклі. Берклі, ймовірно, був би дуже радий теоремі Белла. Доктор Джонсон, звичайно, виступав проти Берклі і звик сперечатися проти своєї філософії, спонукаючи «Я спростовую це таким чином!» при цьому ногами велику скелю. Очевидно, Джонсон знайшов достатній комфорт від свого аргументу, що він не проти поранити ногу.
D'espagnat також схильний вважати, що реальність припущення є неправильним. Таким чином, він писав: «Вчення про те, що світ складається з об'єктів, існування яких не залежить від людської свідомості, виявляється в конфлікті з квантовою механікою та фактами, встановленими експериментом».
У всесвіті участі я можу стверджувати, що ви зобов'язані своїм об'єктивним існуванням моєму доброму втручанню в те, щоб дозволити вам у моїй власній свідомості. Таким чином, в цій позиції присутній властивий соліпсизм. Вігнер був одним з багатьох, кого це сильно турбувало.
НЕ-МІСЦЕВІСТЬ І ДЕВІД БОМ
Нагадаємо, що Девід Бом вирушив на початку 1950-х на пошуки прихованих змінних. Ніхто не досліджував наслідки того, що такі змінні є нелокальними глибше, ніж Бом, і в першому підрозділі нижче ми обговоримо деякі його роботи на цю тему. У наступному підрозділі ми обговоримо його подальше мислення про природу світу.
Неявний порядок
Хорошим посиланням на матеріал цього підрозділу є Девід Бом, Цілісність і Неявний порядок. Хоча дуже глибока книга не є технічною, за винятком глави 4, яка, на мою думку, не повинна була бути включена.
Бом назвав наш повсякденний світ простору, часу і причинності експлікаційним порядком. Він запропонував, що в основі цього повсякденного світу лежить взаємопов'язаний, який він називає неявним порядком. Він використовував ряд аналогів і образів для обговорення цих двох порядків.
В одній аналогії він уявив велику циліндричну скляну ємність з гліцерину, встановлену на вертушці. Розміщуємо пляма чорної фарби в гліцерин. Повільно обертаємо ємність, і чорнило поступово розходиться по всьому гліцерину. Якщо ми повільно обертаємо циліндр у зворотному напрямку, пляма чорнила поступово знову утворюється. Коли чорнило розсіюється, вона знаходиться в неявному стані: вона існує по всьому гліцерину. Коли чорнило є плямою, це експлікація: вона існує в одній частині гліцерину, але не в інших частині. Якщо ми продовжимо обертати циліндр в цьому протилежному напрямку, пляма знову розійдеться.
Розширюємо зображення наступним чином. Розміщуємо пляма чорнила, як і раніше. Ми повільно обертаємо циліндр на один оборот, і чорнило почало розсіюватися. Ми розміщуємо другу пляму чорнила поруч з тим місцем, де було перше місце, і обертаємо ще один оборот. Третє місце знаходиться поруч з тим, де було друге, ще один оборот, і ми продовжуємо це протягом декількох місць. Потім продовжуємо повільно обертати циліндр, поки всі чорнило не розійдуться повністю. Коли ми змінюємо напрямок обертання, ми бачимо останнє місце злиття, потім наступний до останнього праворуч біля останнього, і так далі. Ми могли б інтерпретувати те, що ми бачимо, як єдине пляма чорнила, яке рухається. Таким чином, в задіяному повністю розпорошеному стані ми охопили рух у просторі та часі об'єкта по всьому гліцерину. Реверсивний поворот розгортає реальність назад у простір і час.
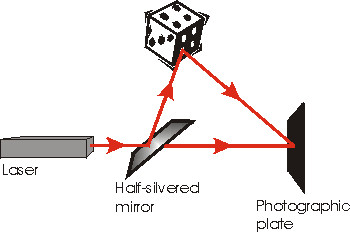Ще одна аналогія - голограма. Як показано праворуч, для виготовлення голограми ми розбиваємо лазерний промінь на дві частини наполовину посрібленим дзеркалом. Один шматок йде прямо на фотографічну пластину, інший відскакує від предмета, а потім йде на тарілку. Для того щоб реконструювати зображення предмета, просвічуємо лазерним променем крізь розроблену пластину: з'являється тривимірне зображення. Зверніть увагу, що в деякому сенсі голограма на тарілці є інтерференційною картиною між променем, який пережив річ, і променем, який відчував нічого.
Однією з характеристик голограми є те, що, по крайней мере, до декількох зерен срібла в пластині, кожен шматок пластини містить все зображення. Якщо ми розрізаємо пластину навпіл, ми не втрачаємо половину зображення; замість цього ми втрачаємо роздільну здатність, і зображення стає більш нечітким. Таким чином, кожен шматок пластини містить весь простір об'єкта в складеному вигляді; це аналогія з неявним порядком. Коли ми реконструюємо зображення, ми розгорнули неявний порядок на експлікаційний.
Існують «мультиплексовані» голограми, які також містять інформацію про час. Якщо об'єкт рухається, обертаємо фотопластину. Коли ми реконструюємо зображення, якщо дивитися під різними кутами, ми бачимо рух об'єкта. Тут тимчасова поведінка об'єкта також укладено в сукупність.
Ми бачимо, що в неявному порядку немає просторового або часового поділу. Таким чином, це нелокальний порядок.
Ось ще одне зображення, яке використовує Бом:
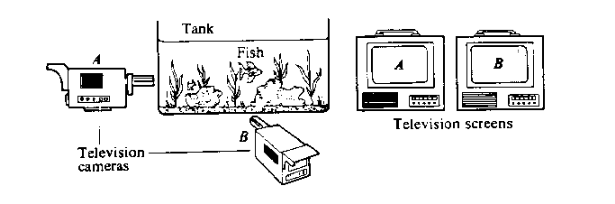
Він коментує: «Зображення на екранах - це дві розмірні проекції (або грані) тривимірної реальності... Однак, оскільки ці проекції існують лише як абстракції, тривимірна реальність не є жодною з них... Те, що насправді знайдено [в експериментальних теоремах Белла], полягає в тому, що поведінка двох [електронів] корелюється таким чином, що досить схожий на поведінку двох телевізійних зображень риби, як описано раніше. Таким чином... кожен електрон діє так, ніби це проекція вищої вимірної реальності... Тут ми пропонуємо зрозуміти квантову властивість нелокального, непричинного зв'язку віддалених елементів через розширення поняття, описаного вище». — стор. 187-188.
Наступна таблиця порівнює explicate і неявний порядок:
| Експлікація | Мають на увазі |
|---|---|
| частини складають ціле | цілі складають деталі |
| просторовий поділ | голографічних |
| описуваний | «палець, що вказує на місяць» |
| речі існують | «річ» і «ніщо» заважають |
| «десять тисяч речей» | ілюзія |
| простор час | спектри |
Враховуючи непорушену цілісність причетного порядку, Бом запитав, чому в нашій думці так переважає фрагментація.
«... фрагментація постійно спричиняється майже універсальною звичкою приймати зміст нашої думки для «опису світу таким, яким він є».» - стор. 3.
Він також писав про те, що з цим робити:
«[Медитація] особливо важлива, тому що... ілюзія того, що я і світ розбиті на фрагменти, бере свій початок у вигляді думки, яка виходить за рамки належної міри і плутає свій власний продукт з тією ж незалежною реальністю. Щоб покінчити з цією ілюзією, потрібно проникливість не тільки в світ в цілому, але і в те, як працює інструмент думки». - стор. 25.
Онтологія Бома квантової механіки
У філософії гносеологія - це вивчення того, що ми знаємо і як ми це знаємо; це на відміну від онтології, яка вивчає те, що насправді існує. Більшість інтерпретацій квантової механіки були розроблені людьми, які співчувають ідеї всесвіту участі; ми обговорювали цю ідею вище. Тому ці тлумачення по суті є гносеологією.
Для Бома це було недостатньо добре. Він розробив онтологію в свої пізніші роки. Його майстер-робота «Нерозділений Всесвіт» була написана разом зі своїм співробітником B.J. Hiley і опублікована в 1993 році. Він написаний для фізиків, і я не можу рекомендувати його нетехнічній аудиторії. Тут ми коротко розглянемо деякі висновки з цієї книги.
По суті, Бом і його школа повторно інтерпретували математику квантової механіки і витягли частину рівняння, яке вони назвали квантовим потенціалом. Квантовий потенціал нелокальний і відповідає за всі нелокальні ефекти, передбачені теорією.
Квантовий потенціал спрямовує, скажімо, шлях електрона таким чином, як радіомаяк може керувати літаком, що приїжджає на посадку в аеропорту. Саме струмені, елерони, кермо і т.д. на площині механічно визначають, куди прямує літак, але маяк направляє шлях.
В онтології Бома електрони дійсно є частинками. Наприклад, для експерименту з подвійною щілиною для електронів кожен електрон проходить або через верхню щілину, або нижню щілину; він має певний шлях, незалежний від його спостереження. Однак квантовий потенціал відрізняється залежно від того, відкрита чи закрита інша щілина; оскільки цей потенціал нелокальний, він може миттєво змінитися, якщо інша щілина відкрита або закрита. Таким чином, електронні шляхи різні залежно від того, відкрита інша щілина чи ні.
Ви можете згадати, що для хаотичної системи дуже незначні зміни початкових умов призводять до кардинально різних траєкторій; докладніше про це ви можете прочитати тут. Виявляється, для подвійного щілинного експерименту для електронів рух електрона після того, як він пройшов щілини, хаотично саме в цьому сенсі. Таким чином, навіть невеликі теплові коливання взаємодії електрона з щілинами призводять до того, що майбутній рух електрона стає непізнаним для нас, хоча він суворо детермінований. Таким чином нам здається, що шлях електрона випадковий, хоча насправді це не так.
Ми називаємо фізику перед квантовою механікою класичною; таким чином теорії відносності є класичними. Зазвичай ми характеризуємо класичну теорію як таку, яка включає спостерігачів і строгий детермінізм, тоді як некласична теорія має учасників і випадковість. Якщо тлумачення Бома є правильним, нам потрібно змінити спосіб, яким ми характеризуємо відмінність. Класична теорія є локальною, а некласична - нелокальна; обидві вони строго детерміновані і мають спостерігачів. У Бома була певна надія, що його онтологія матиме експериментально перевірені наслідки, хоча таких експериментів ще не проводилося.
Можливо, ви захочете знати, що в аналізі Бома так званий фотон не є частинкою; це електромагнітне поле, поведінка якого, подібна до частинок, виникає через його взаємодію з квантовим потенціалом.
Зауважте, що в цій роботі Бом нарешті визначив приховану змінну, яку він шукав протягом багатьох років: це квантовий потенціал.
Нелокальність цього потенціалу змусила Бома викликати зображення, дуже схоже на той, який Уілер використовував вище при обговоренні Всесвіту як самозбудженої системи:
«Класична фізика надала дзеркало, яке відображало лише об'єктивну структуру людини, яка була спостерігачем. У цій схемі немає місця для його психічного процесу, який, таким чином, розглядається як окремий або як просто «епіфеномен» об'єктивних процесів... [Через] дзеркало [квантової фізики] спостерігач бачить «себе» як фізично, так і психічно в більшій обстановці Всесвіту в цілому... Більш широко можна сказати, що через людину Всесвіт робить дзеркало, щоб спостерігати за собою». - Бом і Хілі, Нерозділений Всесвіт, стор. 389
Колега зауважив мені, що героїчні спроби Бома тримати реальність окремо від її спостереження, в цій «остаточній» формі, гірші, ніж альтернатива відсутності реальності. Я не знаю про слово гірше, але після теореми Белла щось має дати, будь то реальність, місцевість та/або сама логіка.
Є ще деякі невирішені питання щодо онтології Бома. Наприклад, як обговорювалося в інших місцях, стандартна планетарна модель атома, де електрони обертаються навколо ядра так само, як планети обертаються навколо Сонця, неможлива, тому що згідно з класичним електромагнетизмом такий електрон знаходиться в стані неоднорідного прискореного руху і повинен випромінювати подалі. його енергії, змушуючи його спіраль в ядро. Однак, коли ми думаємо про електрон в його хвильовому аспекті, то коли хвилі знаходяться в стоячій хвилі, це відповідає дозволеним орбітам моделі Бора, і електрони не випромінюють.
Коли ідея трактування електрона як хвилі повністю розроблена квантовою механікою, орбіти є більш складними, ніж зазначені в документі, на який посилається в попередньому пункті.
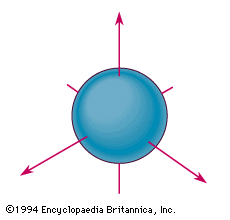Праворуч показуємо «хвильову функцію» для електрона в його наземному стані орбіталі. Видно, що він сферично симетричний. У попередньому обговоренні ми назвали це орбітою, для якої квантове число n дорівнює 1.
В онтології Бома електрон - це частинка. Але для цієї орбіти електрон нерухомий, причому електрична сила намагається втягнути його в протон, просто врівноважується квантовим потенціалом. Таким чином, цей електрон вже точно не буде випромінювати енергію.
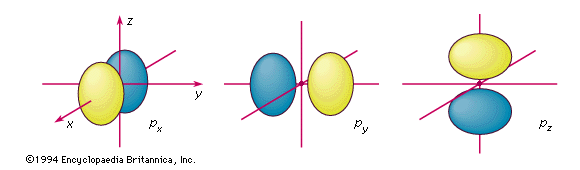
Для стану з принциповим квантовим числом 2 існує сферично симетрична хвильова функція, яка виглядає так само, як показано раніше для n = 1. Але є і три інші орбіталі, які виглядають так, як показано вище.
Для перших двох з цих орбіталів «p» електрони рухаються і прискорюються і, як очікується, випромінюють енергію. Остання p z орбітальна виявляється представляти електрон, який є нерухомим.
Це явно суперечить тому, що електрони в атомі не випромінюють енергію, за винятком випадків, коли вони змінюються з однієї дозволеної орбіти на іншу дозволену орбіту.
Насправді ця складність проявляється в іншій формі в експерименті з подвійною щілиною для електронів. Якщо електрон є частинкою, яка змінює свою траєкторію, коли він проходить через щілини, він теж повинен випромінювати енергію. Один з колег Бома, Віжє, нещодавно сказав, що довжина хвилі цього випромінювання дуже велика, і тому втрати енергії незначні; деякі люди вважають, що Віж'єр помиляється. Наразі ведеться робота над цією проблемою, одним з людей, які працюють над нею, є професор Джон Сіп з цієї кафедри. Мені стало відомо про цю суперечку, намагаючись знайти відповідь на питання, задане колишньою студенткою JPU200Y Шармілою Рейд.
КЛІТИННІ АВТОМАТИ
Клітинний автомат забезпечує ще один підхід до вивчення виникнення структур на основі правил.
Одним з найвідоміших автоматів є Гра життя, розроблена Джоном Конвеєм в 1970 році. Цей приклад відтворюється на великій шаховій сітці. Починається з конфігурації осередків на дошці, які заселяються, а потім обчислює чисельність населення в наступних поколіннях, використовуючи три простих правила:
- Народження: незайнята клітина з рівно 3 зайнятими сусідами буде заселена в наступному поколінні.
- Виживання: зайнята клітина з 2 або 3 зайнятими сусідами буде заселена в наступному поколінні.
- Смерть: у всіх інших випадках клітина незайнята в наступному поколінні.
Незважаючи на простоту правил, в цій грі виникають воістину дивовижні закономірності пересування, складність самоорганізації і багато іншого.
Праворуч - флеш-анімація найпростішої можливої конфігурації, яка змінюється від покоління до покоління, але ніколи не росте і не вимирає.
- Натисніть кнопку Крок, щоб перейти від покоління до покоління. У цьому режимі буде показано кількість зайнятих сусідів кожної клітинки.
- Натисніть кнопку Відтворити, щоб відновити відтворення анімації.
Є багато ресурсів, доступних в Інтернеті, щоб більш детально вивчити цю захоплюючу «гру».
Якщо ви читаєте pdf-версію цього документа, Flash-анімація недоступна з pdf.
Було запропоновано, що ці види автоматів можуть сформувати корисну модель для того, як насправді працює Всесвіт. Серед учасників цієї ідеї Конрад Зузе в 1967 році, Едвард Фредкін на початку 1980-х і зовсім недавно Стівен Вольфрам у 2002 році. Зокрема, робота Вольфрама є результатом майже десятиліття роботи, яка описана в мамонтовій 1200 сторінці самоопублікованої книги скромно під назвою «Новий вид науки».
Є дві ключові особливості клітинних автоматів, які є актуальними для даного обговорення:
- Правила завжди строго детерміновані.
- Еволюція клітини залежить тільки від її найближчих сусідів.
Це, здається, ставить клітинну модель автоматів фізики в конфлікт з теоремою Белла, яка стверджує, що логічна локальна детермінована модель Всесвіту не може бути правильною.
Прихильники моделі клітинних автоматів намагаються стверджувати, що істотного конфлікту немає, лише очевидного. Аргументи включають:
- Що явна випадковість квантових явищ є лише псевдовипадковою. Мені, здається, вони знову вводять ідею прихованих змінних через задні двері. Пламен Петров в одному з прихильників цього аргументу.
- Що існує якась більш вимірна нитка поза нормальними чотирма вимірами простору і часу. Ця «нитка» якось дозволить здійснювати суперпросвітние з'єднання. Вольфрам та інші запропонували цю ідею.
- Інші прихильники Вольфрама стверджували, що швидкість світла є або може бути набагато більше, ніж «звичайне» значення, до якого ми звикли. Чи потрібно це бути нескінченним, незрозуміло.
У попередньому підрозділі Онтологія квантової механіки Бома ми бачили, що спроба Бома зберегти причинність закінчилася абсолютно нелокальним механізмом, інкапсульованим у квантовий потенціал. Навіть там ми побачили в кінці, що є серйозні проблеми з моделлю.
Можливо, є ще більш серйозні проблеми з моделлю Cellular Automaton для способу роботи Всесвіту. Суперечка продовжує бути дуже активною на момент написання цієї статті (весна, 2003). Напіввипадковий список подальших показань:
- arxiv.org/PS_кеш/Квант-рН/ПДФ/0206/0206089.pdf
- http://www.math.usf.edu/~eclark/ANKOS_reviews.html
- http://digitalphysics.org/Publications/Petrov/Pet02m/Pet02m.htm
НАРЕШТІ...
Ейнштейн помер багато років тому, і тому тут не для того, щоб захиститися від претензій на те, що він би чи не зробив би сьогодні. Тим не менш, я схильний думати, що якби він був живий сьогодні, теорема Белла змусила б його прийняти квантову механіку.