28.4: Різні закони швидкості передбачають різну кінетику

Закони різниці швидкості прогнозують різну кінетику

Кінетика нульового порядку

Якщо реакція слідує закону швидкості нульового порядку, вона може бути виражена через часову швидкість зміни [A] (яка буде негативною, оскільки A є реагентом):

\[-\dfrac{d[A]}{dt} = k\]

У цьому випадку просто розділити змінні. Розміщення змінних часу праворуч і [A] ліворуч

\[ d[A] = - k \,dt\]

У такому вигляді його легко інтегрувати. Якщо концентрація А дорівнює [A] ₀ в момент t = 0, а концентрація А [A] в якийсь довільний час пізніше, форма інтеграла дорівнює

\[ \int _{[A]_o}^{[A]} d[A] = - k \int _{t_o}^{t}\,dt\]

який дає

\[ [A] - [A]_o = -kt\]

або

\[ [A] = [A]_o -kt\]

Це говорить про те, що графік концентрації як функція часу дасть пряму лінію, нахил якої дорівнює —k, а перехоплення якої дорівнює [A] ₀. Якщо такий графік лінійний, то дані узгоджуються з кінетикою ^0-го порядку. Якщо їх немає, слід враховувати інші можливості.

Кінетика другого порядку

Якщо реакція слідує закону про ставку другого порядку, певна методологія може бути використана. Ставка може бути записана як

\[ -\dfrac{d[A]}{dt} = k [A]^2 \label{eq1A}\]

Поділ концентрації і тимчасових термінів (на цей раз зберігаючи негативний знак зліва для зручності) дає

\[ -\dfrac{d[A]}{[A]^2} = k \,dt \]

Тоді інтеграція стає

\[ - \int_{[A]_o}^{[A]} \dfrac{d[A]}{[A]^2} = \int_{t=0}^{t}k \,dt \label{eq1}\]

І зауваживши, що

\[ - \dfrac{dx}{x^2} = d \left(\dfrac{1}{x} \right)\]

результат інтеграції Рівняння\ ref {eq1} дорівнює

\[ \dfrac{1}{[A]} -\dfrac{1}{[A]_o} = kt\]

або

\[ \dfrac{1}{[A]} = \dfrac{1}{[A]_o} + kt\]

І тому сюжет\(1/[A]\) як функція часу повинен виробляти лінійний сюжет, нахил якого є\(k\), а перехоплення якого є\(1/[A]_0\).

Інші ^{закони 2-го} порядку трохи складніше інтегрувати, оскільки інтеграція залежить від фактичної стехіометрії досліджуваної реакції. Наприклад, для реакції типу

\[A + B \rightarrow P\]

Це має закони про ставки, наведені

\[ -\dfrac{d[A]}{dt} = k [A][B] \]

і

\[ -\dfrac{d[B]}{dt} = k [A][B] \]

інтеграція буде залежати від зменшення [A] і [B] (що буде пов'язано стехіометрією), що може бути виражено в терміні концентрації продукту [P].

\[[A] = [A]_o – [P] \label{eqr1}\]

і

\[[B] = [B]_o – [P]\label{eqr2}\]

Концентраційна залежність від\(A\) і потім\(B\) може бути усунена, якщо закон норми виражається в терміні виробництва продукту.

\[ \dfrac{d[P]}{dt} = k [A][B] \label{rate2} \]

Підстановка зв'язків для\([A]\) і\([B]\) (Рівняння\ ref {eqr1} і\ ref {eqr2}) у вираз закону швидкості (Equaration\ ref {rate2}) дає

\[ \dfrac{d[P]}{dt} = k ( [A]_o – [P]) ([B] = [B]_o – [P]) \label{rate3} \]

Поділ змінних концентрації та часу призводить до

\[\dfrac{d[P]}{( [A]_o – [P]) ([B] = [B]_o – [P])} = k\,dt\]

Відзначивши\(t = 0\), що в той час\([P] = 0\), інтегрована форма ставка закону може генеруватися шляхом вирішення інтегрального

\[\int_{[A]_o}^{[A]} \dfrac{d[P]}{( [A]_o – [P]) ([B]_o – [P])} = \int_{t=0}^{t} k\,dt\]

Консультації з таблицею інтегралів показує, що для\(a \neq b\) [1],

\[ \int \dfrac{dx}{(a-x)(b-x)} = \dfrac{1}{b-a} \ln \left(\dfrac{b-x}{a-x} \right)\]

Застосування певного інтеграла (до тих пір, поки\([A]_0 \neq [B]_0\)) призводить до

\[ \left. \dfrac{1}{[B]_0-[A]_0} \ln \left( \dfrac{[B]_0-[P]}{[A]_0-[P]} \right) \right |_0^{[A]} = \left. k\, t \right|_0^t\]

\[ \dfrac{1}{[B]_0-[A]_0} \ln \left( \dfrac{[B]_0-[P]}{[A]_0-[P]} \right) -\dfrac{1}{[B]_0-[A]_0} \ln \left( \dfrac{[B]_0}{[A]_0} \right) =k\, t \label{finalint}\]

Підстановка рівнянь\ ref {eqr1} та\ ref {eqr2} на рівняння\ ref {finalint} та спрощення (об'єднання натуральних логарифмічних членів) дає

\[\dfrac{1}{[B]_0-[A]_0} \ln \left( \dfrac{[B][A]_o}{[A][B]_o} \right) = kt\]

За цим нормовим законом, сюжет\(\ln([B]/[A])\) як функція часу буде виробляти пряму лінію, нахил якої дорівнює

\[ m = ([B]_0 – [A]_0)k.\]

У межі в\([A]_0 = [B]_0\), то\([A] = [B]\) в усі часи, за рахунок стехіометрії реакції. Таким чином, закон ставки стає

\[ \text{rate} = k [A]^2\]

і інтегрувати прямий, як у Equation\ ref {Eq1a}, а інтегрований закон швидкості є (як і раніше)

\[ \dfrac{1}{[A]} = \dfrac{1}{[A]_o} + kt\]

Приклад\(\PageIndex{2}\): Confirming Second Order Kinetics

Розглянемо наступні кінетичні дані. Використовуйте графік, щоб продемонструвати, що дані відповідають кінетиці другого порядку. Також, якщо дані другого порядку, визначте значення константи швидкості для реакції.

час (и)	0	10	30	60	100	150	200
[А] (М)	0,238	0.161	0.098	0.062	0.041	0.029	0,023

Рішення:

Сюжет виглядає наступним чином:

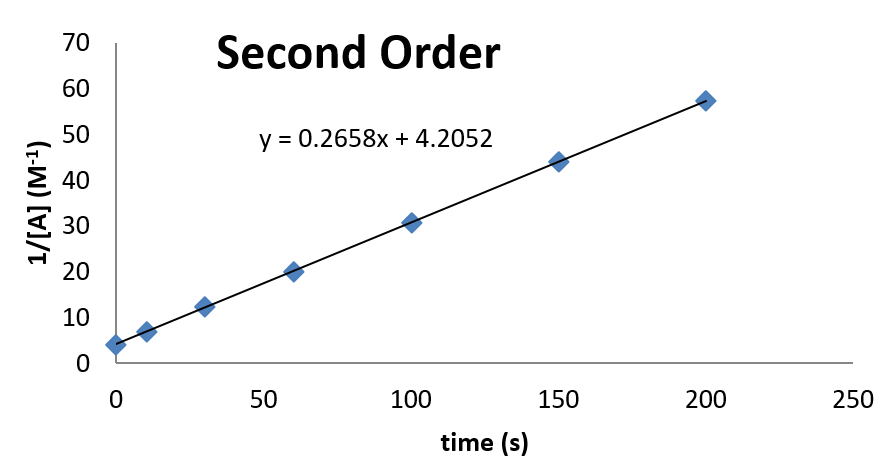
З цієї ділянки видно, що константа швидкості дорівнює 0,2658 М ^-1 с ^-1. Концентрація в часі також\(t = 0\) може бути виведена з перехоплення.

---

[1] Цю інтегральну форму можна генерувати за допомогою методу часткових дробів. Див. (Будинок, 2007) для повного виведення.

Приклад\(\PageIndex{3}\)

Пентоксид азоту (N ₂ O ₅) розкладається до NO ₂ і O ₂ при відносно низьких температурах в наступній реакції:

\( 2N_{2}O_{5}\left ( soln \right ) \rightarrow 4NO_{2}\left ( soln \right )+O_{2}\left ( g \right ) \)

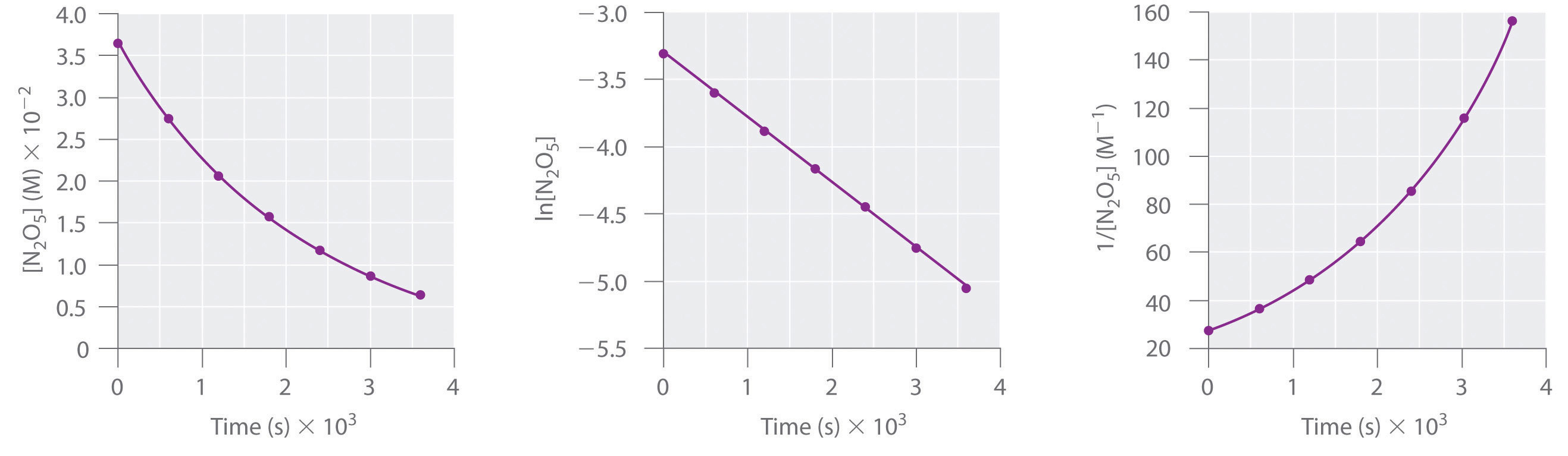
Ця реакція проводиться в розчині cCl ₄ при 45°С, концентрації N ₂ O ₅ в залежності від часу наведені в наступній таблиці разом з природними логарифмами і зворотними концентраціями N ₂ O ₅. Побудувати графік концентрації проти t, ln концентрації проти t, і 1/концентрації проти t, а потім визначити закон швидкості і обчислити константу швидкості.

Час (и)	[N 2 O 5] (М)	лн [Н 2 О 5]	1/ [N 2 О 5] (М ^−1)
0	0.0365	−3.310	27.4
600	0.0274	−3.597	36.5
1200	0.0206	−3.882	48.5
1800	0.0157	−4.154	63.7
2400	0.0117	−4.448	85.5
3000	0,00860	−4.756	116
3600	0,00640	−5.051	156

Задано: збалансоване хімічне рівняння, час реакції та концентрації

Запитано: графік даних, закон швидкості та постійна швидкість

Стратегія:

A Використовуйте дані в таблиці, щоб окремо побудувати концентрацію, природний логарифм концентрації та зворотну концентрацію (вертикальна вісь) проти часу (горизонтальна вісь). Порівняйте графіки з графіками на малюнку 13.4.2, щоб визначити порядок реакції.

B Напишіть закон швидкості для реакції. Використовуючи відповідні дані з таблиці і лінійного графіка, відповідного закону швидкості для реакції, обчислити нахил нанесеної лінії для отримання константи швидкості для реакції.

Рішення:

A Ось ділянки [N ₂ O ₅] проти t, ln [N ₂ O ₅] проти t, і 1/ [N ₂ O ₅] проти t:

Ділянка ln [N ₂ O ₅] проти t дає пряму лінію, тоді як ділянки [N ₂ O ₅] проти t та 1/ [N ₂ O ₅] проти t не роблять. Це означає, що розкладання N ₂ O ₅ знаходиться в першому порядку в [N ₂ O ₅].

B Закон швидкості для реакції, таким чином,

\( rate = k \left [N_{2}O_{5} \right ]\)

Обчислення константи швидкості є простим, оскільки ми знаємо, що нахил ділянки ln [A] проти t для реакції першого порядку дорівнює − k. Ми можемо обчислити нахил, використовуючи будь-які дві точки, які лежать на прямій на ділянці ln [N ₂ O ₅] проти t. Використовуючи точки для t = 0 і 3000 с,

\( slope= \dfrac{ln\left [N_{2}O_{5} \right ]_{3000}-ln\left [N_{2}O_{5} \right ]_{0}}{3000\;s-0\;s} = \dfrac{\left [-4.756 \right ]-\left [-3.310 \right ]}{3000\;s} =4.820\times 10^{-4}\;s^{-1} \)

Таким чином k = 4,820 × 10 ⁻⁴ с ⁻¹.

Дописувачі

Template:ContribLard

Template:ContribHalpernPGCC