20.1: Енергія не визначає спонтанність

Last updated
Save as PDF

Page ID: 27194

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

У природі багато спонтанних подій. При відкритті клапана в обох випадках відбувається мимовільне подія. У першому випадку газ заповнює відкачану камеру, у другому гази будуть змішуватися. Держава функціонує\(U\) і\(H\) не дає нам поняття, що буде. Ви можете подумати, що тільки ті події є спонтанними, які виробляють тепло.

Не так:

Якщо розчинити\(\ce{KNO3}\) у воді, він робить це мимовільно, але розчин стає холодним.
Якщо розчинити\(\ce{KOH}\) у воді, він робить це мимовільно, але розчин стає гарячим.

Зрозуміло, що першого закону недостатньо для опису природи.

Два елементи, що залишилися в нашому списку бажань

Розвиток нової функції стану ентропії наблизило нас набагато ближче до повного розуміння того, як пов'язані тепло і робота:

проблема спонтанності

тепер ми маємо критерій спонтанності для ізольованих систем
асиметрія між роботи-> теплом (розсіюванням) та теплою> роботою (виробництво електроенергії)

принаймні, ми можемо використовувати новий державний закон для прогнозування обмежень щодо останнього.

Залишаються дві проблеми:

ми хотіли б критерій спонтанності для всіх систем (а не лише ізольованих)
у нас нова державна функція\(S\), але що це таке?

Ентропія в мікроскопічному масштабі

Почнемо з останнього. Так, ми можемо використовувати S, щоб пояснити непарний парадокс між w і q обидва істоти утворюють енергію з одного боку, але перетворення легше в одному напрямку, ніж в іншому, але ми ввели поняття ентропія чисто як явище самостійно iis. Науково немає нічого поганого в такій феноменологічній теорії, крім того, що досвід говорить нам, що якщо ви зможете краще зрозуміти саме явище, ваша теорія стає більш потужною.

Щоб краще зрозуміти ентропію, нам потрібно покинути макроскопічний світ і подивитися на те, що відбувається на молекулярному рівні, і зробити статистику по багатьом молекулам. По-перше, давайте зробимо трохи більше статистики такого роду, який нам знадобиться.

Перестановки

Якщо у нас є n помітних об'єктів, скажімо, гральних карт ми можемо розташувати їх у великій кількості способів. Для першого об'єкта в нашій серії у нас є\(n\) вибір, для числа два у нас є\(n-1\) вибір (перший, про який говорять) тощо Це означає, що загалом ми маємо

\[W=n(n-1)(n-2)….4.3.2.1 = n!\;\text{ choices.} \nonumber \]

Величина зазвичай\(W\) називається числом реалізацій в термодинаміці.

Вищесказане вірно, якщо об'єкти всі помітні. Якщо вони потрапляють на групи, в межах яких вони не помітні, ми повинні виправити всі свопи всередині цих груп, які не створюють помітно нового розташування. Це означає, що\(W\) стає\(\frac{n!}{a!b!c!…z!}\) там, де a, b, c to z позначає розмір груп. (Очевидно\(a+b+c+..+z = n\))

У термодинаміці наша «група об'єктів», як правило, являє собою ансамбль систем, думаю про розмір N _av і тому факторіал стає жахливо великим. Це змушує працювати з логарифмами. На щастя, є гарне наближення (Стірлінгом) для логарифмічного факторіала:

\[\ln N! \approx N \ln N-N \nonumber \]

Причинність проти кореляції

В Європі носі маленькі діти, яким цікаво дізнатися, звідки поїхав їхній новонароджений маленький брат або сестра, часто розповідають, що лелека приніс його вночі. Коли ви дивитеся на кількість племінних пар цього прекрасного птаха, наприклад, в Німеччині з 1960 року, ви бачите тривалий спад приблизно до 1980 року, коли птах майже вимерла. Після цього чисельність знову збільшується завдяки програмам розмноження в основному. Рівень народжуваності людини в країні дотримується майже ідентичної кривої, і кореляція між ними дуже висока (> 0,98 або близько того). (Доктор Х. Сіє в природі (том 332 стор. 495; 1988). Чи доводить це, що лелеки дійсно приносять немовлят?

альт — Дорослий білий лелека. з Вікіпедії (кредит: Френк Вассен).

Відповідь:

Ні, це не показує причинності, просто кореляція через загальний основний фактор. У цьому випадку це вибір, зроблений німецьким народом. Спочатку вони зосередилися на тому, щоб працювати по-справжньому наполегливо і мати мало дітей, щоб вийти з бідності Другої світової війни залишила позаду і знехтувала навколишнім середовищем, потім вони звернулися, щоб захистити навколишнє середовище і відкрили двері для імміграції людей, в основному з мусульманських країн, таких як Туреччина чи Марокко, які зазвичай мають великі сім'ї. Урок з цього полягає в тому, що ви можете зробити висновок про причинність лише в тому випадку, якщо ви впевнені, що інших факторів, що втручаються, немає.

Зміна розміру коробки з частинками в ньому

Розширення ідеального газу проти вакууму - це дійсно чудовий модельний експеримент, тому що нічого іншого не відбувається, крім спонтанного розширення та зміни ентропії. Ні зміни енергії, ні тепла, ні роботи, ні зміни маси, ні взаємодій, нічого. Насправді навіть не має значення, вважаємо ми це ізольованим процесом чи ні. Ми могли б так само зробити.

альт

Фізики і фізики люблять знаходити такі експерименти, які дозволяють їм відстежити причинність. Все це означає, що якщо ми подивимося на те, що відбувається на атомному рівні, ми повинні мати можливість відстежити причину зміни ентропії. Як ми бачили раніше, наявні енергетичні стани частинок в коробці залежать від розміру коробки.

\[ E_{kin} = \dfrac{h^2}{8ma^2} \left[ n_1^2 + n_2^2 + n_2^2 \right] \nonumber \]

Зрозуміло, якщо сторона (\(a\)а значить, і обсяг коробки зміниться, енергетичний інтервал між станами стане менше. Тому під час нашого розширення проти вакууму енергетичні стани всередині коробки змінюються. Тому що\(U\) не змінюється середня\(\langle E \rangle\) енергія постійна. Звичайно, це середнє значення береться за велику кількість молекул (систем) в газі (ансамблі), але давайте розглянемо відразу дві з них і для простоти припустимо, що енергія станів рівновіддалена (а не квадратична в квантових числах n).

альт

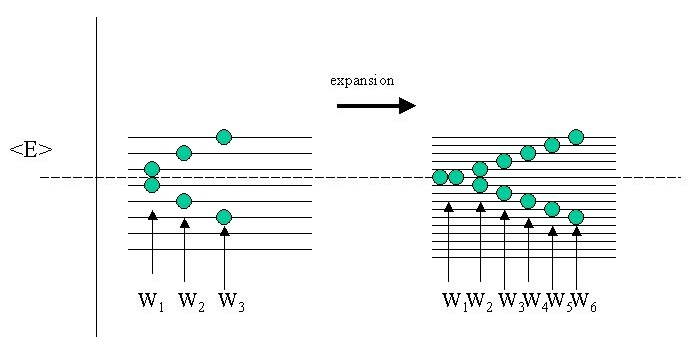
Як бачите, існує не один спосіб обшити кішку, або в цьому випадку реалізувати те ж середнє значення повного ансамблю (всього\(\langle E \rangle\) з двох частинок, за загальним визнанням). Перед розширенням я показав три реалізації W ₁, W ₂, W ₃, які складаються до того ж\(\langle E \rangle\). Однак після розширення є більше енергетичних станів, і на схематичному малюнку показано вдвічі більше реалізацій W в тому ж енергетичному інтервалі.

Больцман першим постулював, що це те, що лежить в основі функції ентропії, а не стільки сама (загальна) енергія (яка залишається незмінною!) , Але кількістю способів енергія може бути розподілена в ансамблі. Зауважте, що оскільки середня (або загальна) енергія ансамблю ідентична, можна також сказати, що різні реалізації\(W\) представляють ступінь \(Ω\)виродження ансамблю.

Больцман вважається набагато більшим (канонічним) ансамблем, що складається з великої кількості однакових систем (наприклад, молекул, але це також можуть бути планети або близько того). Якщо кожна з наших систем вже має велику кількість енергетичних станів, всі системи можуть мати однакову (загальну) енергію, але розподілені досить по-різному. Це означає, що дві системи всередині ансамблю можуть мати однаковий розподіл або інший. Таким чином, ми можемо розділити ансамбль A на підгрупи a _j, що мають однаковий розподіл енергії, і обчислити кількість способів розподілу енергії в ансамблі\(A\), як

\[W= \dfrac{A!}{a1!a2!…}. \nonumber \]

Больцман постулював, що ентропія безпосередньо пов'язана з числом реалізацій W, тобто кількістю способів однієї і тієї ж енергії може бути розподілена в ансамблі. Це призводить відразу до поняття порядку проти розладу, наприклад, якщо кількість реалізацій є\(W=1\), всі системи повинні бути в одному стані (W=A! /А! 0! 0! 0! ...) що є дуже впорядкованим розташуванням енергій.

Якби ми додали два ансамблі один до одного, загальна кількість можливих аранжувань W _tot стає продуктом W ₁ W ₂, але ентропії повинні бути адитивними. Як логарифми перетворюють добуток в доповнення Больцман припустив, що відношення між W і S має бути логарифмічним і пише:

\[S= k \ln W \nonumber \]

Знову ж таки, якщо розглядати дуже впорядкований стан, наприклад, де всі системи знаходяться в наземному стані кількість реалізацій A! /А! = 1, щоб ентропія дорівнювала нулю. Якщо у нас є дуже брудна система, де кількість способів розподілу енергії по безлічі різних станів дуже велика S стає дуже великою. При цьому ентропія дуже велика.

Це відразу дає нам рушійну силу для розширення газу у вакуум або змішування двох газів. Ми просто отримуємо більше енергетичних станів, щоб грати, це збільшує W. Це означає збільшення S. Це призводить до спонтанного процесу.