8.1: Функції двох незалежних змінних
- Page ID
- 18200
(дійсна) функція однієї змінної\(y = f(x)\), визначає криву в площині. Першу похідну функції однієї змінної можна інтерпретувати графічно як нахил дотичної лінії, а динамічно - як швидкість зміни функції щодо змінної Figure\(\PageIndex{1}\).
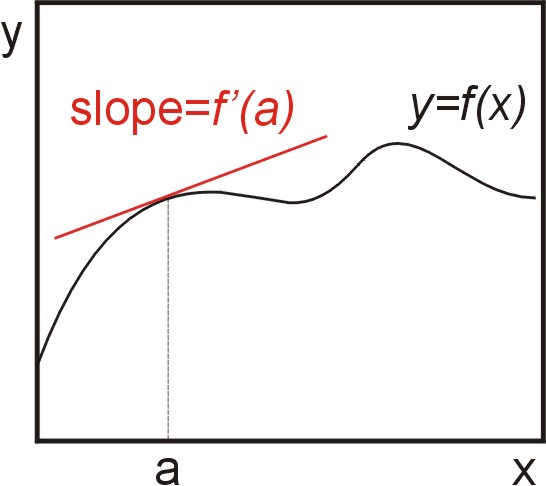
Функція двох незалежних змінних\(z=f (x,y)\), визначає поверхню в тривимірному просторі. Для функції двох або більше змінних існує стільки незалежних перших похідних, скільки незалежних змінних. Наприклад, ми можемо диференціювати функцію\(z=f (x,y)\) щодо\(x\) збереження\(y\) постійної. Ця похідна являє собою нахил дотичної лінії, показаної на малюнку\(\PageIndex{2} \text{A}\). Ми також можемо взяти похідну щодо\(y\) збереження\(x\) постійної, як показано на малюнку\(\PageIndex{2} \text{B}\).
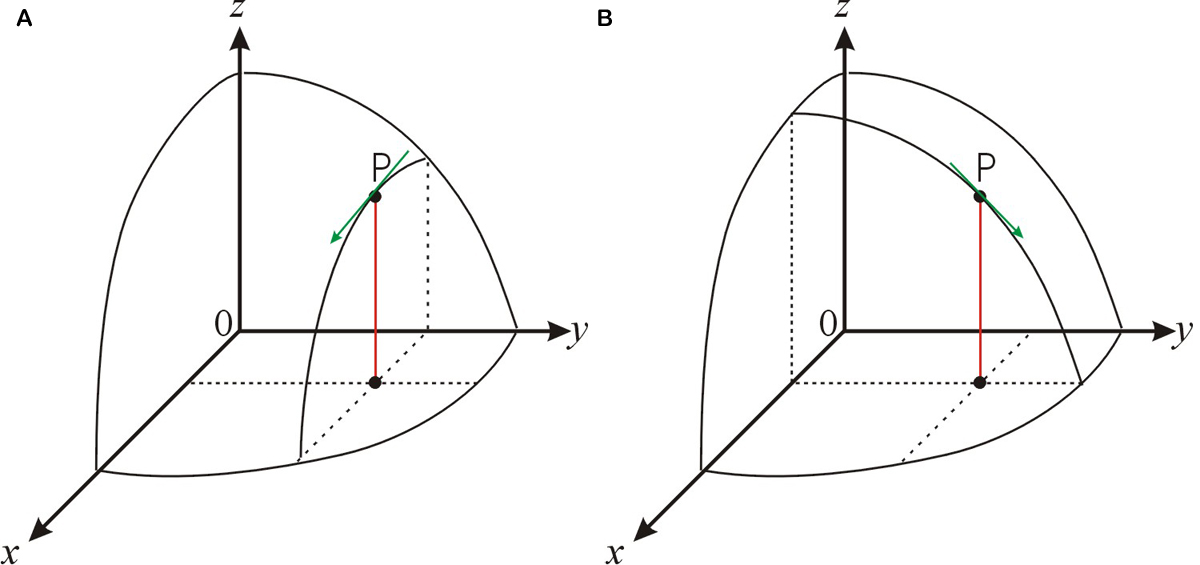
Для прикладу розглянемо функцію\(z=3x^2-y^2+2xy\). Ми можемо прийняти похідну від цієї функції щодо\(x\) трактування\(y\) як константу. Результат є\(6x+2y\). Це часткова похідна функції щодо\(x\), і пишеться вона:
\[\left (\frac{\partial z}{\partial x} \right )_y=6x+2y \nonumber\]
де малі індекси вказують, які змінні утримуються постійними. Аналогічно часткове\(y\) похідне\(z\) щодо це:
\[\left (\frac{\partial z}{\partial y} \right )_x=2x-2y \nonumber\]
Ми можемо розширити ці ідеї на функції більш ніж двох змінних. Наприклад, розглянемо функцію\(f(x,y,z)=x^2y/z\). Ми можемо диференціювати функцію щодо\(x\) збереження\(y\) та\(z\) постійної для отримання:
\[\left (\frac{\partial f}{\partial x} \right )_{y,z}=2x\frac{y}{z} \nonumber\]
Ми також можемо диференціювати функцію щодо\(z\) збереження\(x\) та\(y\) постійності:
\[\left (\frac{\partial f}{\partial z} \right )_{x,y}=-x^2y/z^2 \nonumber\]
і диференціювати функцію щодо\(y\) утримання\(x\) та\(z\) постійної:
\[\left (\frac{\partial f}{\partial y} \right )_{x,z}=\frac{x^2}{z} \nonumber\]
Функції двох або більше змінних можуть бути диференційовані частково більше одного разу щодо будь-якої змінної, утримуючи іншу константу для отримання другої та вищої похідних. Наприклад, функцію\(z=3x^2-y^2+2xy\) можна диференціювати по відношенню до\(x\) двох разів для отримання:
\[\left ( \frac{\partial }{\partial x}\left ( \frac{\partial z}{\partial x} \right )_{y} \right )_{y}=\left ( \frac{\partial ^2z}{\partial x^2} \right )_{y}=6 \nonumber\]
Ми також можемо диференціювати щодо\(x\) першого та\(y\) другого:
\[\left ( \frac{\partial }{\partial y}\left ( \frac{\partial f}{\partial x} \right )_{y} \right )_{x}=\left ( \frac{\partial ^2f}{\partial y \partial x} \right )=2 \nonumber\]
Перевірте відео нижче, якщо ви вивчаєте це вперше, або якщо ви відчуваєте, що вам потрібно оновити концепцію часткових похідних.
- Часткові похідні: http://patrickjmt.com/derivatives-finding-partial-derivatives (не плутайте різні позначення!)
- Часткові похідні: http://www.youtube.com/watch?v=vxJR5graUfI
- Часткові похідні вищого порядку: http://www.youtube.com/watch?v=3itjTS2Y9oE
Якщо функція двох і більше змінних і її похідних є однозначними і неперервними, властивістю, що зазвичай приписується фізичним змінним, то змішані часткові другі похідні рівні (взаємність Ейлера):
\[\label{c2v:euler reciprocity} \left ( \frac{\partial ^2f}{\partial x \partial y} \right )=\left ( \frac{\partial ^2f}{\partial y \partial x} \right )\]
Наприклад, для\(z=3x^2-y^2+2xy\):
\[\left ( \frac{\partial ^2f}{\partial y \partial x} \right )=\left ( \frac{\partial }{\partial y}\left ( \frac{\partial f}{\partial x} \right )_{y} \right )_{x}=\left ( \frac{\partial }{\partial y}\left ( 6x+2y\right ) \right )_{x}=2 \nonumber\]
\[\left ( \frac{\partial ^2f}{\partial x \partial y} \right )=\left ( \frac{\partial }{\partial x}\left ( \frac{\partial f}{\partial y} \right )_{x} \right )_{y}=\left ( \frac{\partial }{\partial x}\left ( -2y+2x\right ) \right )_{y}=2 \nonumber\]
Ще однією корисною властивістю часткових похідних є так звана зворотна ідентичність, яка тримається, коли одні і ті ж змінні утримуються постійними в двох похідних:
\[\label{c2v:inverse} \left ( \frac{\partial y}{\partial x} \right )=\frac{1}{\left ( \frac{\partial x}{\partial y} \right )}\]
Наприклад, для\(z=x^2y\):
\[\left ( \frac{\partial z}{\partial x} \right )_y=\left ( \frac{\partial }{\partial x} x^2y\right )_y=2xy \nonumber\]
\[\left ( \frac{\partial x}{\partial z} \right )_y=\left ( \frac{\partial }{\partial z} \sqrt{z/y} \right )_y=\frac{1}{2y} (z/y)^{-1/2}=\frac{1}{2xy}=\frac{1}{\left ( \frac{\partial z}{\partial x} \right )}_y \nonumber\]
Нарешті, згадаємо правило циклу. Для функції\(z(x,y)\):
\[\label{c2v:cycle} \left ( \frac{\partial y}{\partial x} \right )_z\left ( \frac{\partial x}{\partial z} \right )_y\left ( \frac{\partial z}{\partial y} \right )_x=-1\]
Ми можемо побудувати інші версії наступним чином:
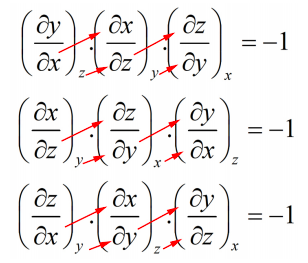
Наприклад, для\(z=x^2y\):
\[\left ( \frac{\partial y}{\partial x} \right )_z=\left ( \frac{\partial }{\partial x} (z/x^2)\right )_z=-2z/x^3 \nonumber\]
\[\left ( \frac{\partial x}{\partial z} \right )_y=\left ( \frac{\partial }{\partial z} \sqrt{z/y}\right )_y=\frac{1}{2y} (z/y)^{-1/2} \nonumber\]
\[\left ( \frac{\partial z}{\partial y} \right )_x=\left ( \frac{\partial }{\partial y} x^2y\right )_x=x^2 \nonumber\]
\[\left ( \frac{\partial y}{\partial x} \right )_z\left ( \frac{\partial x}{\partial z} \right )_y\left ( \frac{\partial z}{\partial y} \right )_x=-\frac{2z}{x^3}\frac{1}{2y} \left(\frac{y}{z}\right)^{1/2}x^2=-\left(\frac{z}{y}\right)^{1/2}\frac{1}{x}=-\left(\frac{x^2y}{y}\right)^{1/2}\frac{1}{x}=-1 \nonumber\]
Перш ніж обговорювати часткові похідні далі, давайте представимо кілька фізико-хімічних понять, щоб поставити нашу дискусію в контексті.