Skip to main content
LibreTexts - Ukrayinska

2.2: Графічне представлення та відносини Ейлера

  1. Last updated
  2. Save as PDF
  • Page ID
    18348

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Комплексні числа можуть бути представлені графічно у вигляді точки в координатній площині. У декартових координатах\(x\) -вісь використовується для дійсної частини числа, а\(y\) -вісь використовується для уявної складової. Наприклад, комплексне число\(x+iy\) представлено у вигляді точки на малюнку\(\PageIndex{1}\).

    Комплексні числа також можуть бути представлені в полярній формі. Ми знаємо, що, враховуючи точку\((x,y)\) в площині,\(\cos\phi=x/r\) і\(\sin\phi=y/r\). Тому комплексне число також\(x+iy\) можна представити у вигляді\(r\cos\phi+i r\sin\phi\).

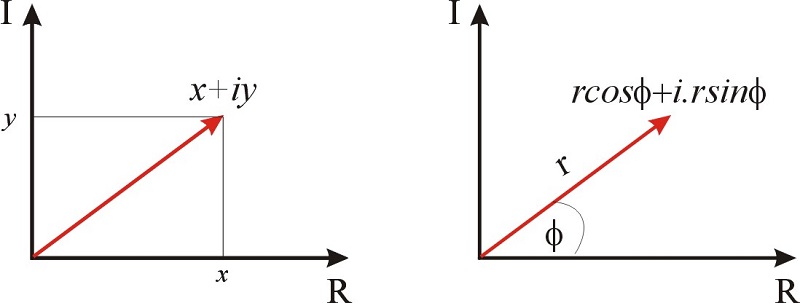
    complex.jpg
    Малюнок\(\PageIndex{1}\): Графічне зображення комплексних чисел. (CC BY-NC-SA; Марсія Левітус)

    Ми також можемо представити комплексні числа через складні експоненціальні. Зараз це буде звучати дивно, але ми побачимо, наскільки це поширене та корисне у фізичній хімії, оскільки ми охоплюємо інші теми цього семестру. Зв'язок Ейлера пов'язує тригонометричні функції до комплексної експоненціальної:

    \[\label{eq1} e^{\pm i\phi}=\cos\phi\pm i\sin\phi\]

    Ми доведемо цей зв'язок за допомогою серії Тейлора пізніше.

    Підсумовуючи, комплексне число\(\displaystyle{\color{Maroon} x+iy}\) може бути виражено в полярних координатах як\(\displaystyle{\color{Maroon}r\cos\phi+i r\sin\phi}\), так і як комплексне експоненціальне як\(\displaystyle{\color{Maroon}r e^{i\phi}}\). Відносини між\(x,y\) і\(r,\phi\) задаються знайомими тригонометричними відносинами:\(x=r\cos\phi\) і\(y=r\sin\phi\). Зауважте, що

    \[r^2=x^2+y^2 \nonumber\]

    і

    \[\sin^2\phi+\cos^2\phi=1 \nonumber\]

    як ми знаємо з теореми Піфагора.

    Приклад\(\PageIndex{1}\)

    Експрес\(z= 1+i\) у формі\(r e^{i\phi}\)

    Рішення

    \(x = 1\)і\(y=1\).

    Ми знаємо, що

    \(x=r\cos\phi\)і\(y=r\sin\phi\)

    Діливши\(y/x\), отримуємо\(y/x=\tan\phi\). У цій\(y=x\) проблемі і тому\(\pi/4\).

    Для отримання\(r\) використовуємо\(r^2=x^2+y^2\). У цьому випадку:

    \[x^2+y^2=2 \to r=\sqrt{2} \nonumber\]

    Тому,\(\displaystyle{\color{Maroon}z = \sqrt{2} e^{\frac{\pi}{4} i}}\)

    З Equation\ ref {eq1} ми бачимо, як тригонометричні функції можуть бути виражені як складні експоненціальні:

    \[ \begin{split} \cos\phi=\frac{e^{i \phi}+e^{-i \phi}}{2}\\ \sin\phi=\frac{e^{i \phi}-e^{-i \phi}}{2i} \end{split}\]

    Знову ж таки, це може виглядати дивно в цей момент, але виявляється, що експоненціальні набагато легше маніпулювати, ніж тригонометричними функціями (подумайте про множення або ділення експоненціальних чисел проти тригонометричних функцій), тому зазвичай фізики пишуть рівняння з точки зору складних експоненціальних косинусів і синусів.

    У Рівняння\(2.1.1\) ми бачили, що\((x+iy)(x-iy)=x^2+y^2\). Тепер ми знаємо, що це дорівнює\(r^2\), де\(r\) модуль або абсолютне значення вектора, представленого червоним кольором на малюнку\(\PageIndex{1}\). Тому модуль комплексного числа, що позначається як\(|z|\), можна обчислити як:

    \[\label{modulus} |z|^2= z z^* \to |z|=\sqrt{z z^*}\]

    Приклад\(\PageIndex{2}\)

    Отримати модуль комплексного числа\(z= 1+i\) (див. Приклад\(\PageIndex{1}\))

    Рішення

    \[|z|=\sqrt{z z^*}=\sqrt{(1+i)(1-i)}=\displaystyle{\color{Maroon}\sqrt{2}} \nonumber\]

    зовнішні посилання