Skip to main content
LibreTexts - Ukrayinska

6.5: Квантові числа

  1. Last updated
  2. Save as PDF
  • Page ID
    27724

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Квантові числа

    Кожен електрон, локалізований в атомі, може бути описаний чотирма квантовими числами. Принцип виключення Паулі говорить нам, що жоден два електрони не можуть розділяти точно такий же набір квантових чисел.

    Основне квантове число

    Принципове квантове число\(n\), представляє енергетичний рівень електрона, подібно до\(n\) використовуваного в моделі Бора. Енергія пов'язана з принципом квантового числа

    \(E=-\dfrac{13.6 \mathrm{eV}}{n^2}, \quad n>0\)

    Орбітальне квантове число кутового імпульсу

    Орбітальний кутовий імпульс квантового числа\(l\), надає інформацію про форму орбіти. На відміну від опису ранніх моделей атома, електрони в атомах не обертаються навколо ядра, як планета навколо Сонця. Однак вони мають кутовий момент, і форма хмари ймовірності навколо ядра залежить від величини моменту моменту. Величина моменту імпульсу пов'язана з орбітальним квантовим числом кутового імпульсу на

    \(L=\hbar \sqrt{l(l+1)}, \quad 0 \leq l \leq n-1\)

    Квантові числа орбітального моменту безпосередньо відповідають буквам, які зазвичай використовуються хіміками для опису орбітальних підоболонок: наприклад,\(l=1\) відповідає\(\mathrm{s}\) орбіталям, які є сферичними:

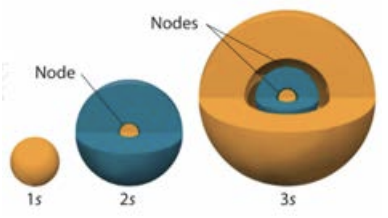
    Знімок екрана 2022-09-06 в 6.00.11 PM.png

    \(l=2\)відповідає\(\mathrm{p}\) орбіталям, які є лопатевими: Візуалізації вищих орбіталів, як\(\mathrm{d}(l-2)\)

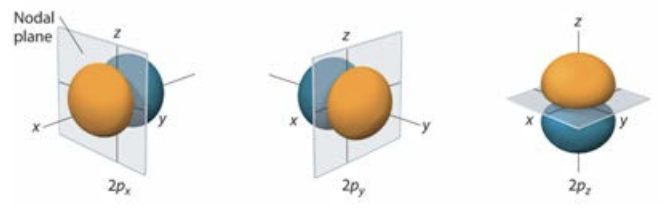
    Знімок екрана 2022-09-06 о 6.03.00 PM.png

    і\(f (l = 3)\) їх можна знайти в главі 6 підручника Аверілла.

    Магнітне квантове число

    Магнітне квантове число відрізняє орбіталі\(m\), доступні в підоболонці. Проекція кутового моменту на\(\mathrm{z}\) вісь -пов'язана з магнітним квантовим числом шляхом

    \(L_z=m \hbar, \quad-l \leq m \leq l\)

    Спін квантове число

    Спінове квантове число\(m_s\), дає спіновий кутовий імпульс кожного електрона. Кожен електрон може обертатися вгору або обертатися вниз. Величина спина або\(+1 / 2\) (спина вгору) або\(-1 / 2\) (спина вниз). Величина моменту моменту, пов'язаного зі спином, дорівнює

    \(|S|=\hbar \sqrt{s(s+1)}\)

    і спінова проекція на\(\mathrm{z}\) вісь -задається

    \(S_z=s \hbar\)

    Обмеження за допустимими значеннями спина становить

    \(s=\pm \dfrac{1}{2}\)

    Приклад: Що таке електронна конфігурація карбону? Випишіть квантові числа для кожного електрона.

    Відповідь

    Вуглець має шість валентних електронів. Ми почнемо заповнювати квантові числа, дотримуючись наведених вище правил. Починаючи з\(n=1\), єдино можливе значення\(l\) є\(l=0\), так як\(0 \leq l \leq n-1\). Коли також\(l=0, m\) має бути 0. Є два можливі спини, які могли б піти з цими квантовими числами. Більше немає доступних квантових чисел\(n=1\), тому ми повинні піднятися до вищої оболонки. Бо\(n=2\), найнижчий енергетичний стан відповідає найменшій величині моменту моменту\(l=0\), що знову ж таки вимагає\(m=0\).

    Для останніх двох електронів ми повинні згадати правило Гунда. Кожна орбіталь в підоболонці повинна бути окремо зайнята електронами одного спіна перед додаванням електронів іншого. Таким чином,\(l=1\) електрони повинні мати різні значення\(m\), але однакове значення\(m_s\). Квантові числа зведені в таблиці нижче.

    \ [\ почати {масив} {c|c|c}
    n & l & m & m_s
    \\\ hline\
    hline 1 & 0 & 0 & 1/2\\
    1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\

    2 & 1 & 0 & 1/2\\
    2 & 1 & -1 & 1/2
    \ кінець {масив}\ nonumber\]