1.6: Вимірювання речовини
- Page ID
- 20175
- Експрес величини правильно, використовуючи число і одиницю.
- Створіть різні вимірювальні системи, що використовуються в хімії.
- Висловіть велику кількість або мале число в науковому позначенні.
- Дізнайтеся, як використовувати префікси SI.
- Виконуйте перетворення одиниць за допомогою коефіцієнтів перетворення.
Інструкція кавоварки підказує вам наповнити кавоварку 4 склянками води і використовувати 3 мірні ложки кави. Коли ви будете слідувати цим інструкціям, ви вимірюєте. При відвідуванні кабінету лікаря медсестра перевіряє температуру, зріст, вагу і, можливо, артеріальний тиск (рис.\(\PageIndex{1}\)); медсестра також вимірює.
Хіміки вимірюють властивості речовини і висловлюють ці вимірювання як величини. Кількість - це кількість чогось, і складається з числа і одиниці. Число говорить нам, скільки (або скільки), а одиниця говорить нам, яка шкала вимірювання. Наприклад, коли відстань повідомляється як «5 кілометрів», ми знаємо, що кількість була виражена в одиницях кілометрів і що кількість кілометрів становить 5. Якщо ви запитаєте друга, як далеко він або вона ходить від дому до школи, а друг відповідає «12», не вказуючи одиницю, ви не знаєте, чи ходить ваш друг 12 миль, 12 кілометрів, 12 фурунгів або 12 ярдів... тощо, щоб правильно висловити кількість, потрібно включити як число, так і одиницю.
Щоб зрозуміти хімію, нам потрібно чітке розуміння одиниць хіміків, з якими працюють і правила, яких вони дотримуються для вираження чисел. Наступні два розділи розглядають правила вираження чисел.
Всі вимірювання залежать від використання одиниць, які добре відомі і зрозумілі. Англійська система одиниць виміру (дюйми, фути, унції і т.д.) не використовуються в науці через труднощі при перетворенні з однієї одиниці в іншу. Метрична система використовується, оскільки всі метричні одиниці базуються на кратних 10, що робить перетворення дуже простими. Метрична система була спочатку створена у Франції в 1795 році. Міжнародна система одиниць - це система вимірювань, заснована на метричній системі. Абревіатура SI зазвичай використовується для позначення цієї системи і розшифровується як французький термін, Le Système International d'Unités. СІ був прийнятий міжнародною угодою в 1960 році і складається з семи базових одиниць, показаних в табл\(\PageIndex{1}\).
| Кількість | Базовий блок SI | Символ |
|---|---|---|
| Довжина | метр | \(\text{m}\) |
| Маса | кілограм | \(\text{kg}\) |
| Температура | Кельвін | \(\text{K}\) |
| Час | другий | \(\text{s}\) |
| Кількість речовини | рити | \(\text{mol}\) |
| Електричний струм | ампер | \(\text{A}\) |
| Інтенсивність світла | кандела | \(\text{cd}\) |
Перші одиниці часто зустрічаються в хімії. Усі інші величини вимірювання, такі як об'єм, сила та енергія, можуть бути отримані з цих семи базових одиниць.
Експоненціальні числа: Сили десяти
Хіміки часто працюють з цифрами, які є надзвичайно великими або малими. Наприклад, введення маси в грамах атома водню в калькулятор вимагатиме відображення з принаймні 24 знаками після коми. Система, яка називається науковою позначенням, дозволяє уникнути значної частини нудності та незручності маніпулювання числами з великими або малими величинами. Крім того, використання префіксів є ще одним способом вираження вимірювань за участю великих і малих чисел.
Наукові позначення
У науковому позначенні числа виражаються у вигляді
\[ N \times 10^n \nonumber \]
де N більше або дорівнює 1 і менше 10 (1 ≤ N < 10), а n - додатне або від'ємне число (10 0 = 1). Число 10 називається базовим, тому що саме це число підвищується в силу\(n\). Хоча базове число може мати значення, відмінні від 10, базове число в наукових позначеннях завжди дорівнює 10.
Простий спосіб перетворення чисел в наукові позначення полягає в тому, щоб перемістити десяткову крапку на стільки знаків вліво або вправо, скільки потрібно, щоб дати число від 1 до 10 (N). Величина n потім визначається наступним чином:
- Якщо десяткову крапку переміщено вліво n знаків, n є додатним.
- Якщо десяткову крапку переміщено вправо n знаків, n є від'ємним.
Інший спосіб запам'ятати це - визнати, що коли число N зменшується за величиною, показник збільшується і навпаки. Застосування цього правила проілюстровано на прикладі\(\PageIndex{1}\).
Перетворіть кожне число в наукові позначення.
- 637,8
- 0.0479
- 12 378
- 0.00032
Рішення
| Пояснення | Відповідь | |
|---|---|---|
| a |
Щоб перетворити 637,8 в число від 1 до 10, переміщаємо десяткову крапку на два розряди вліво: 637,8 Оскільки десяткова крапка була переміщена на два місця вліво, n = 2. |
\(6.378 \times 10^2\) |
| б |
Щоб перетворити 0.0479 в число від 1 до 10, переміщаємо десяткову крапку на два розряди вправо: 0,0479 Оскільки десяткова крапка була переміщена на два місця вправо, n = −2. |
\(4.79 \times 10^{−2}\) |
| c | Оскільки десяткова крапка була переміщена на чотири місця вліво, n = 4. | \(1.2378 \times 10^4\) |
| d | Оскільки десяткова крапка була переміщена на чотири місця вправо, n = −4. | \(3.2 \times 10^{−4}\) |
Перетворіть кожне звичайне число в наукові позначення, або навпаки.
- 67 000 000 000
- 1 689
- 12.6
- Відповідь на
- 6,7 × 10
- Відповідь б
- 1,689 × 10 3
- Відповідь c
- 1,26 × 10 1
Перетворіть кожне звичайне число в наукові позначення, або навпаки.
- 0.000006567
- 6,22 × 10 −2
- 9,9 × 10 −9
- Відповідь на
- 6,567 × 10 −6
- Відповідь б
- 0.0622
- Відповідь c
- 0.0000000099
Метричні префікси
Перетворення між метричними системними одиницями є простими, оскільки система базується на степенях десяти. Наприклад, метри, сантиметри і міліметри - це все метричні одиниці довжини. Є 10 міліметрів в 1 сантиметрі і 100 сантиметрів в 1 метрі. Метричні приставки використовуються для розрізнення одиниць різного розміру. Всі ці префікси походять від латинських або грецьких термінів. Наприклад, мега походить від грецького слова\(\mu \varepsilon \gamma \alpha \varsigma\), що означає «великий». У таблиці\(\PageIndex{2}\) наведено найпоширеніші метричні префікси та їх зв'язок з центральною одиницею, яка не має префікса. Length використовується як приклад для демонстрації відносного розміру кожної префіксної одиниці.
| Префікс | Абревіатура одиниці | Значення | Приклад |
|---|---|---|---|
| гіга | \(\text{G}\) | 1 000 000 000 | 1 гігаметр\(\left( \text{Gm} \right)=10^9 \: \text{m}\) |
| мега | \(\text{M}\) | 1 000 000 | 1 мегаметр\(\left( \text{Mm} \right)=10^6 \: \text{m}\) |
| кіло | \(\text{k}\) | 1 000 | 1 кілометр\(\left( \text{km} \right)=1,000 \: \text{m}\) |
| гекто | \(\text{h}\) | 100 | 1 гектометр\(\left( \text{hm} \right)=100 \: \text{m}\) |
| дека | \(\text{da}\) | 10 | 1 декаметр\(\left( \text{dam} \right)=10 \: \text{m}\) |
| 1 | 1 метр\(\left( \text{m} \right)\) | ||
| деці | \(\text{d}\) | 1/10 | 1 дециметр\(\left( \text{dm} \right)=0.1 \: \text{m}\) |
| центі | \(\text{c}\) | 1/100 | 1 сантиметр\(\left( \text{cm} \right)=0.01 \: \text{m}\) |
| Міллі | \(\text{m}\) | 1/1,000 | 1 міліметр\(\left( \text{mm} \right)=0.001 \: \text{m}\) |
| мікро | \(\mu\) | 1/1 000 000 | 1 мікрометр\(\left( \mu \text{m} \right)=10^{-6} \: \text{m}\) |
| нано | \(\text{n}\) | 1/1 000 000 000 | 1 нанометр\(\left( \text{nm} \right)=10^{-9} \: \text{m}\) |
| піко | \(\text{p}\) | 1/1 000 000 000 000 | 1 пікометр\(\left( \text{pm} \right)=10^{-12} \: \text{m}\) |
Є кілька непарних практик з використанням метричних скорочень. Більшість скорочень мають малі регістри. Ми використовуємо "\(\text{m}\)" для лічильника, а не "\(\text{M}\)». Однак якщо мова йде про обсяг, то базовий агрегат «літр» скорочено позначається як «\(\text{L}\)», а не «\(\text{l}\)». Отже, 3,5 мілілітра пишеться як\(3.5 \: \text{mL}\).
Як практичне питання, коли це можливо, ви повинні висловити одиниці в невеликій і керованій кількості. Якщо ви вимірюєте вагу матеріалу, який важить\(6.5 \: \text{kg}\), це простіше, ніж сказати, що він важить\(6500 \: \text{g}\) або\(0.65 \: \text{dag}\). Всі три правильні, але\(\text{kg}\) агрегати в цьому випадку роблять за невелике і легко кероване число. Однак якщо конкретній проблемі потрібні грами замість кілограмів, йдіть з грамами для консистенції.
Дайте абревіатуру для кожної одиниці і визначте абревіатуру в терміні базової одиниці.
- кілолітр
- мікросекунди
- дециметр
- нанограм
Рішення
| Пояснення | Відповідь | |
|---|---|---|
| a | Приставка кілограм означає «1000 ×», тому 1 кЛ дорівнює 1000 л | кЛ |
| б | Префікс мікро передбачає 1/1000000th одиниці, тому 1 мкс дорівнює 0.000001 с. | мкс |
| c | Приставка деці означає 1/10, тому 1 дм дорівнює 0,1 м. | дм |
| d | Приставка нано означає 1/1000000000, тому нанограм дорівнює 0.000000001 г | нг |
Дайте абревіатуру для кожної одиниці і визначте абревіатуру в терміні базової одиниці.
- кілометр
- міліграм
- наносекунди
- сантилітр
- Відповідь a:
- км
- Відповідь б:
- мг
- Відповідь c:
- нс
- Відповідь d:
- Cl
Маса і вага
Маса - це міра кількості речовини, яку містить об'єкт. Маса предмета проводиться в порівнянні зі стандартною масою в 1 кілограм. Кілограм спочатку визначався як маса\(1 \: \text{L}\) рідкої води при\(4^\text{o} \text{C}\) (обсяг рідини трохи змінюється з температурою). У лабораторії маса вимірюється вагами (див. Нижче), які повинні бути відкалібровані стандартною масою, щоб її вимірювання були точними.

Іншими поширеними одиницями маси є грам і міліграм. Грам становить 1/1000 кілограма, це означає, що є\(1000 \: \text{g}\) в\(1 \: \text{kg}\). Міліграм дорівнює 1/1000-ї частини грама, так що є\(1000 \: \text{mg}\) в\(1 \: \text{g}\).
Масу часто плутають з терміном вага. Вага - це міра сили, яка дорівнює гравітаційної тяги на предмет. Вага об'єкта залежить від його розташування. На Місяці сила, зумовлена гравітацією, становить приблизно одну шосту від сили тяжіння на Землі. Тому даний об'єкт буде важити на Землі в шість разів більше, ніж на Місяці. Оскільки маса залежить лише від кількості речовини, присутньої в об'єкті, маса не змінюється з розташуванням. Вимірювання ваги часто проводяться за допомогою весняної шкали, зчитуючи відстань, яку певний предмет тягне вниз і розтягує пружину.
Довжина і об'єм
Довжина - це вимір ступеня чогось уздовж його найбільшого виміру. Основною одиницею довжини SI, або лінійною мірою, є метр\(\left( \text{m} \right)\). Всі виміри довжини можуть проводитися в метрах, хоча приставки, перераховані в різних таблицях, часто будуть зручніше. Ширина кімнати може бути виражена як близько 5 метрів\(\left( \text{m} \right)\), тоді як велика відстань, наприклад відстань між Нью-Йорком і Чикаго, краще виражати як 1150 кілометрів\(\left( \text{km} \right)\). Дуже малі відстані можуть бути виражені в таких одиницях, як міліметр або мікрометр. Ширина типового людського волоса становить близько 10 мікрометрів\(\left( \mu \text{m} \right)\).

Обсяг - це кількість простору, зайнятого зразком речовини. Обсяг звичайного предмета можна обчислити, помноживши його довжину на ширину і висоту. Оскільки кожен з них є лінійним виміром, ми говоримо, що одиниці об'єму походять від одиниць довжини. Одиницею об'єму СІ є кубічний метр\(\left( \text{m}^3 \right)\), який є об'ємом, зайнятим кубом, який вимірює з кожного\(1 \: \text{m}\) боку. Цей дуже великий обсяг не дуже зручний для типового використання в хімічній лабораторії. Літр\(\left( \text{L} \right)\) - це обсяг куба, який вимірює з кожного\(10 \: \text{cm}\)\(\left( 1 \: \text{dm} \right)\) боку. А літр при цьому дорівнює і тому,\(1000 \: \text{cm}^3\)\(\left( 10 \: \text{cm} \times 10 \: \text{cm} \times 10 \: \text{cm} \right)\) і до\(1 \: \text{dm}^3\).
1Л\(1000 \: \text{cm}^3\)\(\left( 10 \: \text{cm} \times 10 \: \text{cm} \times 10 \: \text{cm} \right)\) =\(1 \: \text{dm}^3\)
Меншою одиницею об'єму, яка зазвичай використовується, є мілілітр (\(\text{mL}\)). Мілілітр - це обсяг куба, який вимірює з кожного\(1 \: \text{cm}\) боку. Тому мілілітр дорівнює кубічному сантиметру\(\left( \text{cm}^3 \right)\).
1 мл\(\left( \text{cm}^3 \right)\)
Є\(1000 \: \text{mL}\) в\(1 \: \text{L}\), що те саме, що сказати, що є\(1000 \: \text{cm}^3\) в\(1 \: \text{dm}^3\).


Під час вивчення хімії (і фізики також) ви зауважите, що математичні рівняння використовуються в багатьох різних додатках. Багато з цих рівнянь мають ряд різних змінних, з якими вам потрібно буде працювати. Слід також зазначити, що ці рівняння часто вимагатимуть від вас використання вимірювань з їх одиницями. Тут дуже важливими стають навички алгебри!
Перетворення між одиницями з коефіцієнтами перетворення
Коефіцієнт перетворення - це коефіцієнт, який використовується для перетворення однієї одиниці виміру в іншу. Простий коефіцієнт перетворення може бути використаний для перетворення метрів в сантиметри, або більш складний може бути використаний для перетворення миль на годину в метри в секунду. Оскільки більшість розрахунків вимагають вимірювання в певних одиницях, ви знайдете багато застосувань для коефіцієнтів перетворення. Завжди пам'ятайте, що коефіцієнт перетворення повинен представляти факт; цей факт може бути або простим, або набагато складнішим. Наприклад, ви вже знаєте, що 12 яєць дорівнюють одному десятку. Більш складним фактом є те, що швидкість світла -\(1.86 \times 10^5\) милі/сек. Будь-який з них може бути використаний як коефіцієнт перетворення, залежно від типу розрахунку, з яким ви можете працювати (Таблиця\(\PageIndex{1}\)).
| Англійські одиниці | Метричні одиниці | Кількість |
|---|---|---|
| 1 унція (унція) | 28.35 грам (г) | *маса |
| 1 рідина один раз (унція) | 2,96 мл | обсяг |
| 2,205 фунтів (фунт) | 1 кілограм (кг) | *маса |
| 1 дюйм (дюйм) | 2.54 сантиметри (см) | довжина |
| 0.6214 миль (миль) | 1 кілометр (км) | довжина |
| 1 чверть (qt) | 0.95 літра (Л) | обсяг |
* Фунти і унції є технічно одиницями сили, а не маси, але цей факт часто ігнорується ненауковим співтовариством.
Звичайно, є й інші співвідношення, які не вказані в табл\(\PageIndex{1}\). Вони можуть включати в себе:
- Співвідношення, вбудовані в текст задачі (з використанням таких слів, як per або в кожному, або з використанням символів, таких як/або%).
- Перетворення в метричній системі, як описано раніше в цьому розділі.
- Загальновідомі співвідношення (наприклад, 60 секунд\(=\) 1 хвилина).
Якщо ви дізналися описані одиниці СІ і приставки, то знаєте, що 1 см - це 1/100 метра.
\[ 1\; \rm{cm} = \dfrac{1}{100} \; \rm{m} = 10^{-2}\rm{m} \nonumber \]
або
\[100\; \rm{cm} = 1\; \rm{m} \nonumber \]
Припустимо, розділимо обидві сторони рівняння на\(1 \text{m}\) (і число, і одиницю):
\[\mathrm{\dfrac{100\:cm}{1\:m}=\dfrac{1\:m}{1\:m}} \nonumber \]
Поки ми виконуємо одну і ту ж операцію з обох сторін знака рівності, вираз залишається рівністю. Подивіться на праву частину рівняння; тепер воно має таку ж величину в чисельнику (верхній), як у знаменнику (внизу). Будь-який дріб, який має однакову величину в чисельнику і знаменнику, має значення 1:
\[ \dfrac{ \text{100 cm}}{\text{1 m}} = \dfrac{ \text{1000 mm}}{\text{1 m}}= \dfrac{ 1\times 10^6 \mu \text{m}}{\text{1 m}}= 1 \nonumber \]
Ми знаємо, що 100 см - це 1 м, тому у нас однакова кількість на верхній і нижній частині нашої фракції, хоча вона виражена в різних одиницях.
Виконання аналізу розмірів
Розмірний аналіз є одним з найбільш цінних інструментів, що використовуються фізичними вченими. Простіше кажучи, це перетворення між сумою в одній одиниці в відповідну суму в потрібну одиницю, використовуючи різні коефіцієнти перерахунку. Це цінно, оскільки певні вимірювання більш точні або легше знайти, ніж інші. Використання одиниць у розрахунку для забезпечення отримання кінцевих належних одиниць називається розмірним аналізом.
Ось простий приклад: Скільки сантиметрів в 3,55 м? Можливо, ви зможете визначити відповідь у себе в голові. Якщо в кожному метрі 100 см, то 3,55 м дорівнює 355 см. Щоб вирішити задачу більш формально з коефіцієнтом перетворення, спочатку запишемо задану нам величину, 3,55 м Потім множимо цю величину на коефіцієнт перетворення, який такий же, як і множення її на 1. Ми можемо записати 1 як\(\mathrm{\frac{100\:cm}{1\:m}}\) і помножити:
\[ 3.55 \; \rm{m} \times \dfrac{100 \; \rm{cm}}{1\; \rm{m}} \nonumber \]
3.55 м можна розглядати як дріб з 1 в знаменнику. Оскільки m, абревіатура для метрів, зустрічається і в чисельнику, і в знаменнику нашого виразу, вони скасовують:
\[\dfrac{3.55 \; \cancel{\rm{m}}}{ 1} \times \dfrac{100 \; \rm{cm}}{1 \; \cancel{\rm{m}}} \nonumber \]
Останнім кроком є виконання розрахунку, який залишається після скасування одиниць:
\[ \dfrac{3.55}{1} \times \dfrac{100 \; \rm{cm}}{1} = 355 \; \rm{cm} \nonumber \]
У остаточній відповіді опускаємо 1 в знаменнику. Таким чином, за більш формальною процедурою ми знаходимо, що 3,55 м дорівнює 355 см. Узагальнене опис цього процесу виглядає наступним чином:
кількість (в старих одиницях) × коефіцієнт перетворення = кількість (в нових одиницях)
Можливо, вам буде цікаво, чому ми використовуємо, здавалося б, складну процедуру для простого перетворення. У більш пізніх дослідженнях проблеми з перетворенням, з якими ви зіткнетеся, не завжди будуть такими простими. Якщо ви зможете освоїти техніку застосування коефіцієнтів перерахунку, вам вдасться вирішити велику кількість різноманітних завдань.
У попередньому прикладі ми використовували дріб\(\frac{100 \; \rm{cm}}{1 \; \rm{m}}\) як коефіцієнт перетворення. Чи коефіцієнт перетворення\(\frac{1 \; \rm m}{100 \; \rm{cm}}\) також дорівнює 1? Так, він має таку ж величину в чисельнику, як і в знаменнику (за винятком того, що вони виражені в різних одиницях). Чому ми не використали цей коефіцієнт перетворення? Якби ми використовували другий коефіцієнт перетворення, вихідну одиницю не скасували б, а результат був би безглуздим. Ось що ми б отримали:
\[ 3.55 \; \rm{m} \times \dfrac{1\; \rm{m}}{100 \; \rm{cm}} = 0.0355 \dfrac{\rm{m}^2}{\rm{cm}} \nonumber \]
Щоб відповідь була значущою, ми повинні побудувати коефіцієнт перетворення у формі, яка змушує вихідну одиницю скасувати. \(\PageIndex{1}\)На малюнку показана концептуальна карта для побудови належного перетворення.
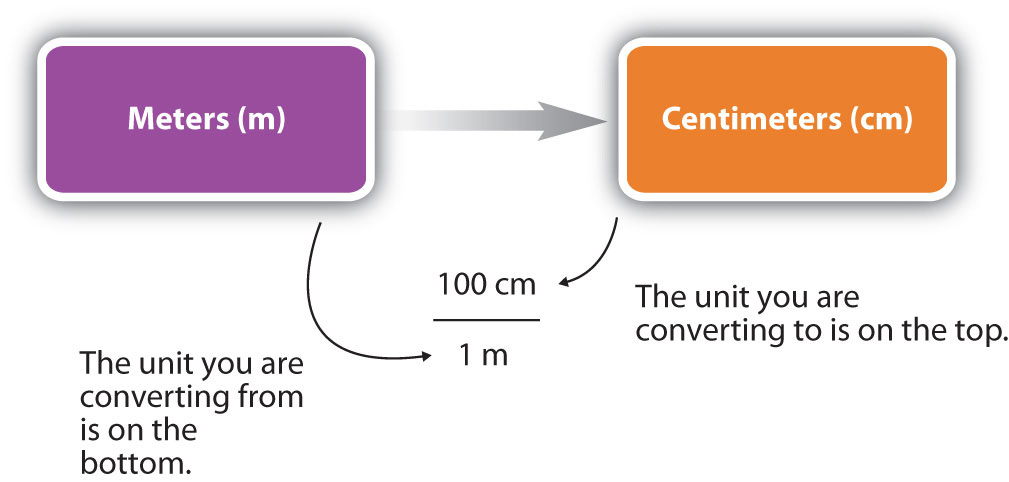
- Визначте "задану" інформацію в проблемі. Шукайте число з одиницями, щоб почати цю проблему.
- У чому проблема з проханням "знайти «? Іншими словами, яку одиницю матиме ваша відповідь?
- Використовуйте коефіцієнти та коефіцієнти конверсії, щоб скасувати одиниці, які не є частиною вашої відповіді, і залиште одиниці, які є частиною вашої відповіді.
- Коли ваші одиниці скасують правильно, ви готові зробити математику. Ви множите дроби, тому ви множите верхні числа і ділите на нижні числа в дробах.
| Приклад\(\PageIndex{2}\) | Приклад\(\PageIndex{3}\) | |
|---|---|---|
| Кроки для вирішення проблем | \ (\ pageIndex {2}\)» style="text-align:center; вертикально-вирівнюється:middle; ">Середній об'єм крові у дорослого чоловіка становить 4,7 л. Що це за обсяг в галонів? | \ (\ pageIndex {3}\)» style="text-align:center; вертикальне вирівнювання: середина; ">Колібрі може махати крилами один раз в 18 мс. Скільки секунд в 18 мс? |
| Визначте «дану» інформацію і те, що проблема просить вас «знайти». | \ (\ pageIndex {2}\)» style="вирівнювання тексту: по центру; вертикальне вирівнювання: середина; "> Задано: 4.7 L Знайти: гал |
\ (\ pageIndex {3}\)» style="вирівнювання тексту: по центру; вертикальне вирівнювання: середина; "> Задано: 18 мс Знайти: s |
| Перерахуйте інші відомі величини. | \ (\ PageIndex {2}\)» style="вирівнювання тексту: центр; вертикальне вирівнювання: середина; ">\(1\, L = 3.785 gal \) | \ (\ PageIndex {3}\)» style="вирівнювання тексту: центр; вертикальне вирівнювання: середина; ">\(1 \,ms = 10^{-3} s \) |
| Підготуйте концептуальну карту і використовуйте правильний коефіцієнт перетворення. | \ (\ індекс сторінки {2}\)» style="вертикальне вирівнювання: середина; "> |
\ (\ індекс сторінки {3}\)» style="вертикальне вирівнювання: середина; ">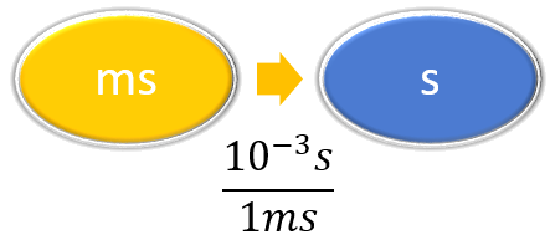 |
| Скасуйте одиниці та розрахуйте. | \ (\ PageIndex {2}\)» style="вирівнювання тексту: центр; вертикальне вирівнювання: середина; ">\( 4.7 \cancel{\rm{L}} \times \dfrac{1 \; \rm{gal}}{3.785\; \cancel{\rm{L}}} = 1.2\; \rm{gal}\) | \ (\ індекс сторінки {3}\)» style="вертикальне вирівнювання: середина; ">
\( 18 \; \cancel{\rm{ms}} \times \dfrac{10^{-3}\; \rm{s}}{1 \; \cancel{\rm{ms}}} = 0.018\; \rm{s}\) або \( 18 \; \cancel{\rm{ms}} \times \dfrac{1\; \rm{s}}{1,000 \; \cancel{\rm{ms}}} = 0.018\; \rm{s}\) |
| Подумайте про свій результат. | \ (\ pageIndex {2}\)» style="text-align:center; vertical-align:middle; ">Сума в gal повинна бути трохи меншою за 4 рази менше заданої кількості в L. | \ (\ pageIndex {3}\)» style="vertical-align:middle; ">Сума в s повинна бути 1/1000 задана сума в мс. |
Виконайте кожне перетворення.
- 101,000 нс в секунди
- 32.08 кг в грами
- 1,53 грама в кг
- Відповідь:
- \(1.01000 x 10^{-4} s \)
- Відповідь б:
- \(3.208 x 10^{4} g \)
- Відповідь c:
- \(1.53 x 10^{2} g \)
Кілька конверсій
Іноді вам доведеться виконати більше одного перетворення, щоб отримати потрібну одиницю. Наприклад, припустимо, ви хочете перетворити 54,7 км в міліметри. Ми встановимо ряд коефіцієнтів перетворення так, щоб кожен коефіцієнт перетворення створював наступну одиницю в послідовності. W e спочатку перетворюють задану суму в км в базову одиницю, яка є метрами. Ми знаємо, що 1000 м =1 км. Потім ми перетворюємо метри в мм, пам'ятаючи, що\(1\; \rm{mm}\) =\( 10^{-3}\; \rm{m}\).
Концепція Карта
Розрахунок
\[ \begin{align} 54.7 \; \cancel{\rm{km}} \times \dfrac{1,000 \; \cancel{\rm{m}}}{1\; \cancel{\rm{km}}} \times \dfrac{1\; \cancel{\rm{mm}}}{\cancel{10^{-3} \rm{m}}} & = 54,700,000 \; \rm{mm} \\ &= 5.47 \times 10^7\; \rm{mm} \end{align} \nonumber \]
На кожному кроці попередній блок скасовується і проводиться наступний блок у послідовності; кожен наступний блок скасовується, поки не залишиться лише одиниця, необхідна у відповіді.
Перетворіть 58.2 мс в мегасекунди за один багатоступінчастий розрахунок.
Рішення
Кроки для вирішення проблем |
Конвертація одиниць |
|---|---|
| Визначте «дану» інформацію і те, що проблема просить вас «знайти». |
Дано: 58.2 мс Знайти: Ms |
| Перерахуйте інші відомі величини. |
\(1 ms = 10^{-3} s \) \(1 Ms = 10^6s \) |
| Підготуйте концептуальну карту. |
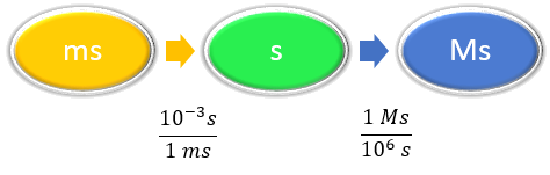
|
| Розрахувати. |
\[ \begin{align} 58.2 \; \cancel{\rm{ms}} \times \dfrac{10^{-3} \cancel{\rm{s}}}{1\; \cancel{\rm{ms}}} \times \dfrac{1\; \rm{Ms}}{1,000,000\; \cancel{ \rm{s}}} & =0.0000000582\; \rm{Ms} \nonumber\\ &= 5.82 \times 10^{-8}\; \rm{Ms}\nonumber \end{align}\nonumber \] Жоден коефіцієнт перерахунку не впливає на кількість значущих цифр у підсумковій відповіді. |
Скільки секунд в день?
Рішення
Кроки для вирішення проблем |
Конвертація одиниць |
|---|---|
| Визначте «дану» інформацію і те, що проблема просить вас «знайти». |
Подарували: 1 день Знайти: s |
| Перерахуйте інші відомі величини. |
1 день = 24 години 1 година = 60 хвилин 1 хвилина = 60 секунд |
| Підготуйте концептуальну карту. |
|
| Розрахувати. | \[1 \: \text{d} \times \frac{24 \: \text{hr}}{1 \: \text{d}}\times \frac{60 \: \text{min}}{1 \: \text{hr}} \times \frac{60 \: \text{s}}{1 \: \text{min}} = 86,400 \: \text{s} \nonumber \] |
Виконайте кожне перетворення в одному багатоступінчастому обчисленні.
- 43.007 нг до кг
- 1005 дюймів у фути
- 12 км до км
- Відповідь:
- \(4.3007 x 10^{-14} kg \)
- Відповідь б:
- 83.75 футів
- Відповідь c:
- 19 км
Резюме
- Метричні префікси походять від латинських або грецьких термінів. Префікси використовуються для того, щоб зробити одиниці керованими.
- Система СІ заснована на кратних десяти. У системі СІ є сім основних одиниць. П'ять з цих одиниць зазвичай використовуються в хімії.
- Маса - це міра кількості речовини, яку містить об'єкт.
- Вага - це міра сили, яка дорівнює гравітаційної тяги на предмет.
- Маса не залежить від місця розташування, тоді як вага залежить від місця розташування.
- Довжина - це вимір ступеня чогось уздовж його найбільшого виміру.
- Обсяг - це кількість простору, зайнятого зразком речовини.
- Обсяг можна визначити, знаючи довжину кожної сторони виробу.
- Коефіцієнти перетворення використовуються для перетворення однієї одиниці виміру в іншу.
- Аналіз розмірів (перетворення одиниць) передбачає використання коефіцієнтів перетворення, які скасують небажані одиниці і вироблять потрібні одиниці.
Автори та атрибуція
- Template:ContribCK12
- Template:ContribAgnewM
- Template:ContribAgnewH
- Template:ContribGordon
- Hayden Cox (Furman University)