2.2: PSS.2- Значні цифри

Last updated
Save as PDF

Page ID: 25572

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Визначте кількість значущих цифр у повідомленому значенні.

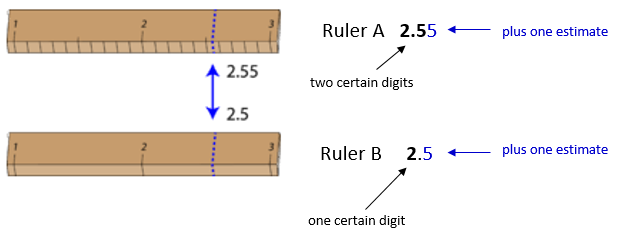
Значні цифри у вимірюванні складаються з усіх певних цифр у цьому вимірі плюс одна невизначена або передбачувана цифра. На ілюстрації лінійки нижче нижня лінійка дала довжину з 2 значущими фігурами, тоді як верхня лінійка давала довжину з 3 значущими фігурами. У правильно повідомленому вимірюванні кінцева цифра є значною, але не певною. Незначні цифри не повідомляються. З будь-якою лінійкою неможливо було б повідомити довжину,\(2.553 \: \text{cm}\) оскільки немає можливого способу оцінки тисячних цифр. 3 не є значним і не буде повідомлено.

Малюнок\(\PageIndex{1}\): Вимірювання двома різними лінійками.

Невизначеність вимірювання

Якась похибка або невизначеність завжди існує в будь-якому вимірі. Величина невизначеності залежить як від майстерності вимірювача, так і від якості вимірювального інструменту. У той час як деякі баланси здатні вимірювати маси тільки до найближчого\(0.1 \: \text{g}\), інші високочутливі баланси здатні вимірювати до найближчого\(0.001 \: \text{g}\) або навіть краще. Багато вимірювальних інструментів, таких як лінійки та градуйовані циліндри, мають невеликі лінії, які потрібно уважно прочитати, щоб зробити вимірювання. \(\PageIndex{1}\)На малюнку зображені дві лінійки, які роблять однаковий вимір об'єкта (позначені синьою стрілкою).

За допомогою будь-якої лінійки зрозуміло, що довжина предмета знаходиться між\(2\) і\(3 \: \text{cm}\). Нижня лінійка не містить міліметрових розміток. За допомогою цієї лінійки можна оцінити десяту цифру, а довжину можна повідомити як\(2.5 \: \text{cm}\). Однак інша людина може судити про те, що вимірювання є\(2.4 \: \text{cm}\) чи можливо\(2.6 \: \text{cm}\). У той час як 2 відомо напевно, значення десятих цифр є невизначеним.

Верхня лінійка містить позначки на десяті частки сантиметра (міліметри). Тепер можна виміряти той же об'єкт, що і\(2.55 \: \text{cm}\). Вимірювач здатний оцінити цифру сотих, оскільки він може бути впевнений, що цифра десятих - це 5. Знову ж таки, інший вимірювач може повідомити довжину бути\(2.54 \: \text{cm}\) або\(2.56 \: \text{cm}\). У цьому випадку є дві певні цифри (2 і 5), при цьому цифра сотих є невизначеною. Зрозуміло, що верхня лінійка - це чудова лінійка для вимірювання довжини якомога точніше.

Приклад\(\PageIndex{1}\): Reporting Measurements to the Proper Number of Significant Figures

Використовуйте кожну діаграму, щоб повідомити про вимірювання до належної кількості значущих цифр.

а. Барометр вимірювання одиниць psi з голкою від 4,0 до 5,0

б.

Лінійка, що вимірює прямокутник в одиницях сантиметрів, з краєм прямокутника між позначками 1,2 і 1,3 см

Рішення

Рішення до прикладу 2.3.1
	Пояснення	Відповідь
а.	Стрілка знаходиться в межах від 4,0 до 5,0, тому вимірювання становить не менше 4,0. Стрілка знаходиться між третьою і четвертою невеликими галочками, так що це не менше 0,3. Доведеться прикинути останнє місце. Це виглядає приблизно на третину шляху через простір, тому оцінимо соті місця як 3. Символ psi розшифровується як «фунтів на квадратний дюйм» і є одиницею тиску, як повітря в шині. Вимірювання повідомляється на три значущі цифри.	4,33 фунтів на квадратний дюйм
б.	Прямокутник шириною не менше 1,0 см, але, звичайно, не шириною 2,0 см, тому перша значна цифра - 1. Ширина прямокутника перевищує другу галочку, але не третю; якщо кожна галочка дорівнює 0,1, то прямокутник буде принаймні 0,2 в наступній значній цифрі. Ми повинні оцінити наступне місце, тому що немає маркувань, які б нас орієнтували. Здається, це приблизно на півдорозі між 0,2 і 0,3, тому ми оцінимо наступне місце, щоб бути 5. Таким чином, виміряна ширина прямокутника дорівнює 1,25 см. Вимірювання повідомляється на три значущі цифри.	1,25 см

Вправа\(\PageIndex{1}\)

Якою буде ширина цього прямокутника?

Лінійка вимірює прямокутник в сантиметрах, край прямокутника між позначками 1,2 і 1,3 см

Відповідь: 1,25 см

Коли ви дивитеся на повідомлене вимірювання, необхідно вміти підраховувати кількість значущих цифр. У таблиці нижче детально описані правила визначення кількості значущих цифр в повідомленому вимірі. Для прикладів в таблиці припустимо, що величини - це правильно повідомлені значення виміряної величини.

Таблиця\(\PageIndex{1}\): Правила значущих фігур
Правило	Приклади
1. Усі ненульові цифри у вимірюванні є значними.	237 має три значущі цифри. 1.897 має чотири значущі цифри.
2. Нулі, що з'являються між іншими ненульовими цифрами (середні нулі), завжди значні.	39 004 має п'ять значущих цифр. 5.02 має три значущі цифри.
3. Нулі, які з'являються перед усіма ненульовими цифрами, називаються провідними нулями. Провідні нулі ніколи не є значними.	0,008 має одну істотну цифру. 0.000416 має три значущі цифри.
4. Нулі, які з'являються після всіх ненульових цифр, називаються кінцевими нулями. Число з кінцевими нулями, якому не вистачає десяткової крапки, може бути значним або не може бути значним. Використовуйте наукові позначення для позначення відповідної кількості значущих цифр.	1400 - неоднозначний. \(1.4 \times 10^3\)має дві значущі цифри. \(1.40 \times 10^3\)три значущі цифри. \(1.400 \times 10^3\)має чотири значущі цифри.
5. Прикінцеві нулі в числі з десятковою крапкою є значними. Це вірно, чи виникають нулі до або після коми.	620.0 має чотири значущі цифри. 19.000 має п'ять значущих цифр.

Точні цифри

Цілі числа, отримані або шляхом підрахунку об'єктів, або з визначень, є точними числами, які, як вважається, мають нескінченно багато значущих цифр. Якщо ми нарахували, наприклад, чотири об'єкти, то число 4 має нескінченну кількість значущих цифр (тобто воно являє собою 4.000...). Аналогічно, 1 фут (фут) визначається як містити 12 дюймів (дюймів), тому число 12 у наступному рівнянні має нескінченно багато значущих цифр:

Приклад\(\PageIndex{2}\)

Наведіть кількість значущих цифр в кожному. Визначте правило для кожного.

5.87
0.031
52.90
00.2001
500
6 атомів

Рішення

Рішення до прикладу 2.3.2
	Пояснення	Відповідь
a	Всі три числа є значущими (правило 1).	5.87, три значущі цифри
б	Провідні нулі не є значними (правило 3). 3 і 1 є значущими (правило 1).	0,031, дві значущі цифри
c	5, 2 і 9 є значущими (правило 1). Значущим є і кінцевий нуль (правило 5).	52.90, чотири значущі цифри
d	Провідні нулі не є значними (правило 3). 2 і 1 є значущими (правило 1), а середні нулі також є значними (правило 2).	00.2001, чотири значущі цифри
е	Число неоднозначне. Він міг мати одну, дві або три значущі цифри.	500, неоднозначний
f	6 є рахунковим числом. Підрахувальне число - це точне число.	6, нескінченний

Вправа\(\PageIndex{2}\)

Наведіть кількість значущих цифр в кожному.

36.7 м
0.006606 с
2,002 кг
306 490 000 осіб
3 800 г

Відповідь: три значущі цифри

Відповідь б: чотири значущі цифри

Відповідь c: чотири значущі цифри

Відповідь d: нескінченне (точне число)

Відповідь e: Неоднозначні, можуть бути дві, три або чотири значущі цифри.

Точність і точність

Вимірювання можуть бути точними, тобто виміряне значення збігається з істинним значенням; вони можуть бути точними, а це означає, що кілька вимірювань дають майже однакові значення (тобто відтворювані результати); вони можуть бути як точними, так і точними; або вони не можуть бути ні точними, ні точними. Метою вчених є отримання вимірюваних значень, які є одночасно точними і точними. Відео нижче демонструє поняття точності і точності.

Відео\(\PageIndex{1}\): Різниця між точністю і точністю.

Приклад\(\PageIndex{3}\)

Наступні мішені для стрільби з лука показують позначки, які представляють результати чотирьох наборів вимірювань.

Мета A: 2 мітки разом на середньому кільці, B: злегка розкидані мітки біля центру, C: позначки близько в центрі, D: позначки, розкидані по всьому кільцю

Яку ціль показує

точний, але неточний набір вимірювань?
набір вимірювань, який є одночасно точним і точним?
набір вимірювань, які не є ні точними, ні точними?

Рішення

Встановити a точний, але неточний.
Набір c є одночасно точним і точним.
Набір d не є ні точним, ні точним.

Резюме

Невизначеність існує у всіх вимірах. На ступінь невизначеності частково впливає якість вимірювального інструменту. Значні цифри дають вказівку на достовірність вимірювання. Правила дозволяють приймати рішення про те, скільки цифр використовувати в будь-якій ситуації.