23.2: Теорія Крамерса

У нашому лікуванні рух реагенту над перехідним станом трактувався як вільний перехідний ступінь свободи. Цей балістичний або інерційний рух не є репрезентативним для динаміки в м'якій речовині при кімнатній температурі. Теорія Крамерса є провідним підходом до опису перетину дифузійного бар'єру. На нього припадає тертя і термічне перемішування, які зменшують частку успішних переходів бар'єрів. Знову ж таки, швидкості отримують від потоку над бар'єром вздовж координати реакції, Рівняння (23.1).

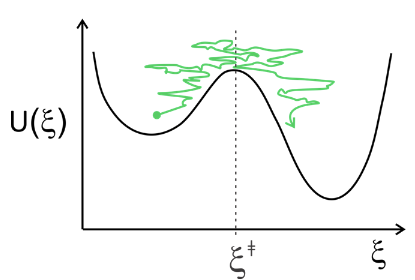
Одним із підходів є лікування дифузійного перетину бар'єру в потенціалі за допомогою рівняння Смолуховського. Дифузійний потік під впливом потенціалу має два внески:

1. Градієнт концентрації\(dC/dξ\). Пропорційно коефіцієнту дифузії,\(D\).
2. Сила від градієнта потенціалу.

\[ J(\xi)=-D \frac{d C(\xi)}{d \xi}-\frac{C(\xi)}{\zeta} \frac{d U(\xi)}{d \xi} \nonumber\]

Як обговорювалося раніше\(ζ\), це коефіцієнт тертя і в одному вимірі:

\[ \zeta=\frac{k_{B} T}{D} \nonumber\]

Написано з точки зору щільності ймовірності\(P\)

\[\begin{align*} J &=D\left(-\frac{P}{k_{B} T} \frac{d U}{d \xi}-\frac{d P}{d \xi}\right) \\ &=-D e^{-U / k_{B} T} \frac{d}{d \xi}\left(P e^{U / k_{B} T}\right) \end{align*}\]

або

\[ J e^{U / k_{B} T}=-D \frac{d}{d \xi} P e^{U / k_{B} T} \]

Тут ми припустили, що\(D\) і не\(ζ\) є функціями\(ξ\).

Наступне важливе припущення теорії Крамерса полягає в тому, що ми можемо вирішити для дифузійного потоку, використовуючи стаціонарне наближення. Це дозволяє нам встановити:\(J\) = константу. \(ξ\)Інтегруйте вздовж бар'єру.

\[ \begin{align*} J \int_{a}^{b} e^{U / k_{B} T} d \xi * &=-D \int_{a}^{b} d P e^{U / k_{B} T} \\[4pt]  J \int_{a}^{b} e^{U(\xi) / k_{B} T} d \xi &=D\left\{P_{R} e^{U_{R} / k_{B} T}-P_{P} e^{U_{P} / k_{B} T}\right\} \end{align*}\]

\(P_i\)є ймовірностями зайняття\(R\) або\(P\) держави, і\(U_i\) є енергіями\(R\) і\(P\) станів. Права частина цього рівняння описує чистий потік через бар'єр.

Розглянемо тільки flux\(R\longrightarrow P\) from:\( J_{R\longrightarrow P} \), який ми робимо шляхом установки\(P_P\longrightarrow 0\). Це просто проблема втечі з бар'єру. Також в якості точки відліку ставимо\(U_R(ξ_R) = 0\).

\[ J_{R \rightarrow P}=\frac{D P_{R}}{\int_{a}^{b} e^{U(\xi) / k_{B} T} d \xi} \label{23.2.2}\]

Потік лінійно пропорційний коефіцієнту дифузії і ймовірності знаходження в реактивному стані. Потік зменшується фактором, який описує енергетичний бар'єр, який потрібно подолати. Тепер давайте оцінимо з конкретною формою потенціалу. Найпростіша форма -\(U(ξ)\) моделювати параболами. Колодязь реагенту задається

\[ U_{R}=\frac{1}{2} m \omega_{R}^{2}\left(\xi-\xi_{R}\right)^{2} \label{23.2.3}\]

і ставимо\(\xi_R \longrightarrow 0\). Бар'єр моделюється перевернутою параболою з центром у перехідному стані з висотою бар'єру для прямої реакції\(E_f\) та шириною, заданою бар'єрною частотою\(ω_{bar}\):

\[ U_{\mathrm{bar}}=E_{f}-\frac{1}{2} m \omega_{\mathrm{bar}}^{2}\left(\xi-\xi^{‡}\right)^{2} \nonumber\]

По суті, це трактування еволюції розподілу ймовірностей як руху фіктивної частинки з масою\(m\).

Спочатку оцінюємо знаменник в Equation\ ref {23.2.2}. \(e^{U_{bar}/k_BT}\)це щільність ймовірності, яка досягла максимуму\( \xi^‡\), тому зміна меж на інтеграл не впливає на речі сильно.

\[\int_{a}^{b} e^{U_{b a r} / k_{B} T} d \xi \approx \int_{-\infty}^{+\infty} d \xi \exp \left[-\frac{m \omega_{B}^{2}\left(\xi-\xi^{‡}\right)^{2}}{2 k_{B} T}\right]=\sqrt{\frac{2 \pi k_{B} T}{m \omega_{B}^{2}}} \nonumber\]

Тоді рівняння\ ref {23.2.2} стає

\[ J_{R \rightarrow P}=\omega_{\text {bar }} D \sqrt{\frac{m}{2 \pi k_{B} T}} e^{-E_{f} / k_{B} T} P_{R} \label{23.2.4}\]

Далі давайте оцінимо\(P_R\). Для гауссової ями в рівнянні\ ref {23.2.3} щільність ймовірності вздовж\(ξ\) дорівнює\(P_R = e^{-U_{R} / k_{B} T}\):

\[ P_{R}(\xi)=\exp \left[-\frac{1}{2} m \omega_{R}^{2}\left(\xi-\xi_{R}\right)^{2} / k_{B} T\right] \nonumber\]

\[ P_{R} \approx \int_{-\infty}^{+\infty} P_{R}(\xi) d \xi=\omega_{R} \sqrt{\frac{m}{2 \pi k_{B} T}} \nonumber\]

Підставляючи це в рівняння\ ref {23.2.4}, ми маємо

\[ J_{R \rightarrow P}=\omega_{R} \omega_{b a r} D\left(\frac{m}{2 \pi k_{B} T}\right) e^{-E_{f} / k_{B} T} \nonumber\]

Використовуючи відношення Ейнштейна\( D = k_BT/\zeta \), ми знаходимо, що прямий потік масштабується обернено тертям (або в'язкістю).

\[ J_{R \rightarrow P}=\frac{\omega_{R}}{2 \pi} \frac{\omega_{b a r}}{\zeta} e^{-E_{f} / k_{B} T} \]

Також фактор\(m\) зникає, коли проблема виражається в масово зважених координатах\(\omega_{\text {bar }}=\sqrt{m} \omega_{\text {bar }}\). Зверніть увагу на схожість Рівняння (9) з теорією перехідного стану. Якщо зв'язати період частинки в свердловині реагенту з частотою перетину бар'єру,

\[ \frac{\omega_{R}}{2 \pi} \Rightarrow v=\frac{k_{B} T}{h} \nonumber\]

то ми також можемо знайти, що ми вираз для коефіцієнта передачі в цій моделі:

\[ k_{diff}=\kappa_{diff} k_{TST} \nonumber\]

\[ \kappa_{diff}=\dfrac{\omega_{bar}}{\zeta}\ll 1 \nonumber\]

Це швидкість реакції в сильному демпфузійному, або дифузійному, межі. Хендрік Крамерс фактично вирішив більш загальну задачу, засновану на рівнянні Фоккера - Планка, яке описувало проміжне та сильне демпфування. Швидкість реакції була описана як

\[ k_{Kr}=\kappa_{Kr} k_{TST} \nonumber\]

\[\kappa_{K r}=\frac{1}{\omega_{b a r}}\left(-\frac{\zeta}{2}+\sqrt{\frac{\zeta^{2}}{4}+\omega_{b a r}^{2}}\right) \nonumber\]

\[ \zeta=\frac{1}{m k_{B} T} \int_{0}^{\infty} d t\langle\xi(0) \xi(t)\rangle \nonumber\]

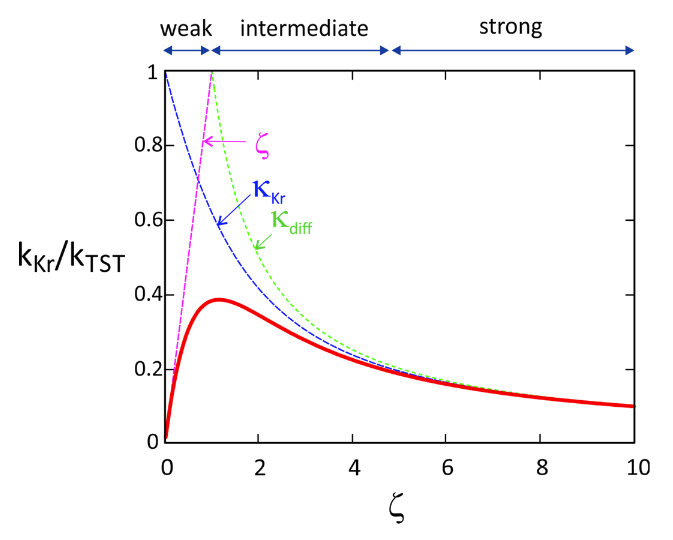
Це показує кросовер у поведінці між сильним демпфузійним (або дифузійним) поведінкою, описаним вище, та проміжним режимом демпфузії:

• Сильне гасіння/тертя:\(\zeta \longrightarrow \infty\)\(\kappa_{Kr}\longrightarrow\dfrac{\omega_{bar}}{\zeta} \nonumber\)
• Проміжне демпфування:\(\zeta <<2\omega_B\)\(\kappa_{Kr}\longrightarrow 1\) і\(k_{Kr}\longrightarrow k_{TST} \nonumber\)

У слабкій межі тертя Крамерс стверджував, що швидкість реакції масштабується як

\[k_{\text {weak }} \sim \zeta k_{T S T} \nonumber\]

Тобто, якби у вас взагалі не було тертя, частинка просто рухалася б вперед і назад між реагентом і станом продукту, не вчиняючись певної свердловини. Вам потрібно деяке розсіювання, щоб незворотно розслабитися в продукті. Виходячи з цього, ми очікуємо оптимального тертя\(κ\), яке максимізується, що врівноважує потребу в деякому розсіюванні, але без такої кількості, що перетин бар'єру надзвичайно рідкісний. Цей «оборот Крамерса» фіксується формулою інтерполяції

\[\kappa^{-1}=\kappa_{K r}^{-1}+\kappa_{\text {weak }}^{-1} \nonumber\]