17.4: Полімеризація храповик і транслокаційний храповик

Last updated
Save as PDF

Page ID: 18068

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Полімеризація і транслокаційні тріскачки відносяться до процесів, які призводять до спрямованих зміщень полімерної або олігомерної ланцюга або, а не специфічного білка. Моделі для цих тріскачок також передбачають випрямлений броунівський рух, при якому вузол зв'язування є доданим до дифузійної ланцюга для зміщення дифузійного руху в потрібному напрямку. Після того, як витіснення ent досягає певної довжини дифузії, мономер або зв'язування prot ein може додати до ланцюга, блокуючи в прямій дифузії ланцюга. У цьому випадку саме зв'язування або приєднання білкових одиниць споживає енергію, як правило, у вигляді гідролізу АТФ o r GTP.

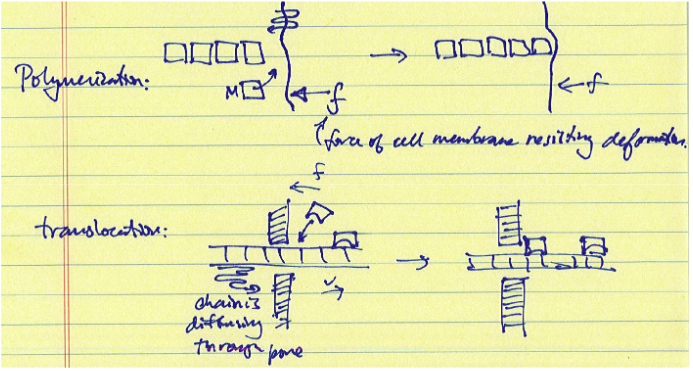
Транслокація Ratchet ¹

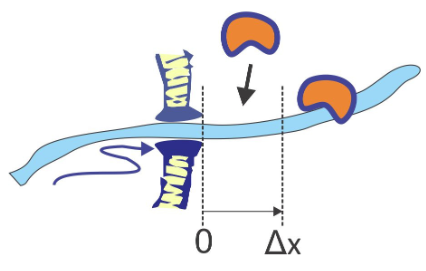Транслокація білка через мембрани льоду - це всюдисущий професійний шах для транспортування поліпептидних ланцюгів через бактеріальні та органельні мембрани через канали s за допомогою білків шаперону на внутрішній стороні е мембрана. Транслокація r тріповик відноситься до моделі, в якій транспорт ланцюга відбувається через броунівський рух, який випрямляється зв'язуванням білків з ланцюгом на одній стороні пори при її зміщенні. Після того, як ланцюг дифузно s через пори на відстань Δ x, білок може зв'язуватися з ланцюгом, зупиняючи зворотну дифузію. На кожному кроці потрібна енергія, щоб керувати зв'язуванням білка шаперону.

Транслокаційна храповик відноситься до моделі континууму для d диффузії ланцюга. Цю задачу дифузії можна зіставляти на рівняння Смолуховського, але для щільності ймовірності її було б важко розв'язати. Простіше, якщо ми просто зацікавлені в описі середньої швидкості ланцюга в умовах сталого стану, ми можемо вирішити для stead y-state ланцюговий потік через пору:

\[J(x) = -D \left( \dfrac{\partial P}{\partial x} + \dfrac{f}{k_BT}P \right) \]

where f is the force acting against the chain displacement. Steady state behavior corresponds to \( \partial P/\partial t =0 \) , so from the continuity equation

\[ \dfrac{\partial P}{\partial t} = -\dfrac{\partial J}{\partial x} \nonumber \]

we know that \(\partial J/\partial x = 0 \). Therefore J is a constant. To find P, we want to solve

\[ \dfrac{\partial P}{\partial x} + \dfrac{f}{k_BT}P+\dfrac{J}{D} = 0 \nonumber \]

for which the general solution is \(P=A_1e^{-fx/k_BT}+A_2\). We find the integration constants using the boundary condition \(P(\Delta x,t )=0 \), which reflects that a protein will immediately and irreversibly bind once the diffusing chain reaches an extension \(\Delta x\). (No back-stepping is allowed.) And we use the conservation statement:

\[ \int_0^{\Delta x} dx P(x) = 1 \nonumber \]

which says that a protein must be bound within the interval 0 to Δx. The steady-state probability distribution with these two boundary conditions is

\[ P(x) = \dfrac{ \underset{ \sim }{f} \left[ \exp \left( \underset{ \sim }{f} (1-x/\Delta x) \right) -1 \right] }{\Delta x\left( 1+ \underset{ \sim }{f} - e^{ \underset{ \sim }{f} } \right) } \]

\[ \underset{ \sim }{f} = \dfrac{f \Delta x}{k_BT} \nonumber \]

\( \underset{\sim}{f}\) is a dimensionless constant that expresses the load force in units of k_BT opposing ratchet displacement by Δx.

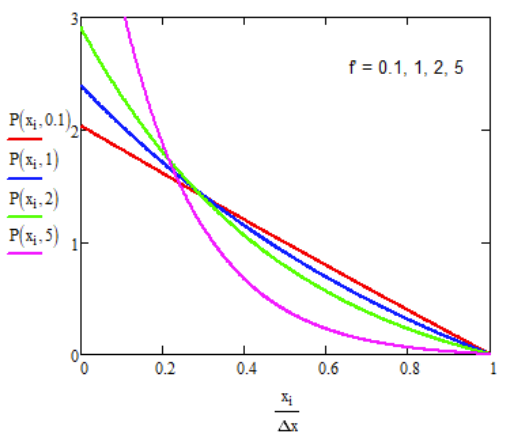
Substituting eq. (17.4.2) into eq. (17.4.1) allows us to solve for J.

\[J(x) =\dfrac{-D\underset{ \sim }{f}^2 }{\Delta x^2\left( 1+ \underset{ \sim }{f}-e^{\underset{ \sim }{f}} \right) } \left( 1-2\exp \left[ \underset{ \sim }{f} \left( \dfrac{x}{\Delta x} -1 \right) \right] \right) \nonumber \]

Now, the average velocity can be determined from \(\langle \nu \rangle = J\Delta x \). Evaluating the flux at x = Δx:

\[ \langle \nu \rangle =\dfrac{2D}{\Delta x} \left[ \dfrac{\underset{ \sim }{f}^2/2}{e^{\underset{ \sim }{f}}-\underset{ \sim }{f}-1} \right] \nonumber \]

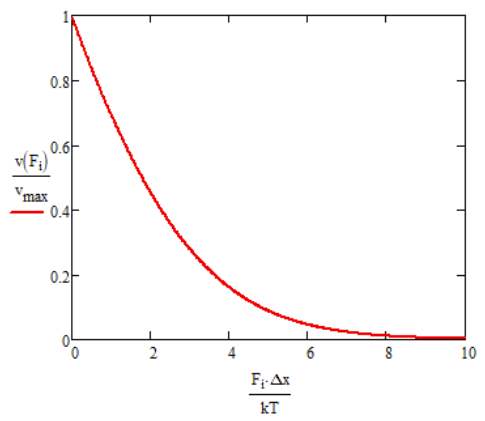
Now look at low force limit \(f \rightarrow 0 \). Expand \(e^{\underset{ \sim }{f}}=1+\underset{ \sim }{f}+\underset{ \sim }{f}^2/2 \):

\[ \langle \nu \rangle \rightarrow \dfrac{2D}{\Delta x} = v_{max} \nonumber \]

Note that this is the maximum velocity for ideal ratchet, and it follows the expected behavior for pure diffusive motion.

Now consider probability of the protein binding is governed by equilibrium between free and bound forms:

\[ F \overset{k_a}{\underset{k_d} \rightleftharpoons} B \qquad \qquad K= \dfrac{k_a}{k_d} = \dfrac{\tau_B}{\tau_F} \nonumber \]

Here k_a refers to the effecting quasi-first-order rate constant for binding at a chaperone concentration [chap]: \(k_a = k_a' [ chap ] \).

Fast kinetics approximation

\[ \begin{aligned} &\langle \nu \rangle = \dfrac{2D}{\Delta x} \left[ \dfrac{\underset{ \sim }{f}^2/2}{\dfrac{e^{\underset{ \sim }{f}}-1}{1-K(e^{\underset{ \sim }{f}}-1)}-\underset{ \sim }{f}} \right] \\ &\langle \nu \rangle_{max} = \dfrac{2D}{\Delta x} \left( \dfrac{1}{1+2K} \right) \end{aligned} \]

Stall Load

\[ f_0 = \dfrac{k_BT}{\Delta x} \ln \left( 1+ \dfrac{1}{K} \right) \nonumber \]

________________________________

C. S. Peskin, G. M. Odell and G. F. Oster, Cellular motions and thermal fluctuations: the Brownian ratchet, Biophys. J. 65 (1), 316–324 (1993).