12.1: Односторонній нормальний розподіл

Last updated

Oct 25, 2022
Save as PDF
- 12: Додатки
- 12.2: Критичні значення для Т-тесту

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Таблиця $\PageIndex{1}$ , внизу цього додатка, дає пропорцію, P, площі під нормальною кривою розподілу, яка лежить праворуч від відхилення, z

$z = \frac {X -\mu} {\sigma} \nonumber$

де X - значення, для якого визначено відхилення, $\mu$ є середнім значенням розподілу і $\sigma$ стандартним відхиленням розподілу. Наприклад, частка площі при нормальному розподілі праворуч від відхилення 0,04 дорівнює 0,4840 (див. запис червоним кольором в таблиці), або 48,40% від загальної площі (див. Площа заштрихована синім кольором на малюнку $\PageIndex{1}$ ). Частка площі вліво від відхилення становить 1 — П. Для відхилення 0,04 це 1 — 0,4840, або 51,60%.

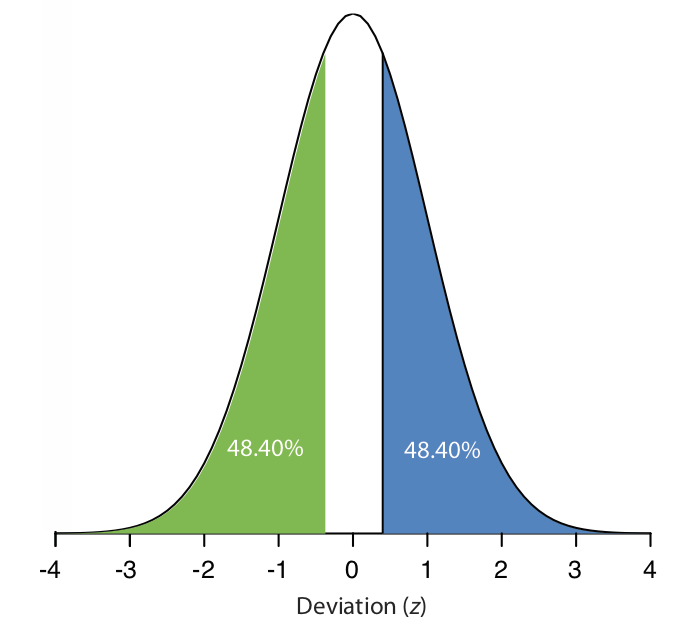
Рис Додаток 3.1.png

Малюнок $\PageIndex{1}$ . Нормальна крива розподілу, що показує площу під кривою більше відхилення +0,04 (синій) і з відхиленням менше —0,04 (зелений).

Коли відхилення від'ємне, тобто коли X менше $\mu$ —значення z від'ємне. При цьому значення в таблиці дають площу зліва від z. Наприклад, якщо z дорівнює —0,04, то 48,40% площі лежить зліва від відхилення (див. Область, заштрихована зеленим кольором на рис $\PageIndex{1}$ .

Щоб використовувати односторонню таблицю нормального розподілу, намалюйте нормальну криву розподілу для вашої задачі та затіньте область, яка відповідає вашій відповіді (наприклад, див. Рис. $\PageIndex{2}$ , Наприклад, 4.4.2).

Малюнок $\PageIndex{2}$ . Нормальний розподіл для населення таблеток аспірину в прикладі 4.4.2. Середнє значення популяції і стандартне відхилення - 250 мг і 5 мг відповідно. Затінена область показує відсоток таблеток, що містять між 243 мг і 262 мг аспірину.

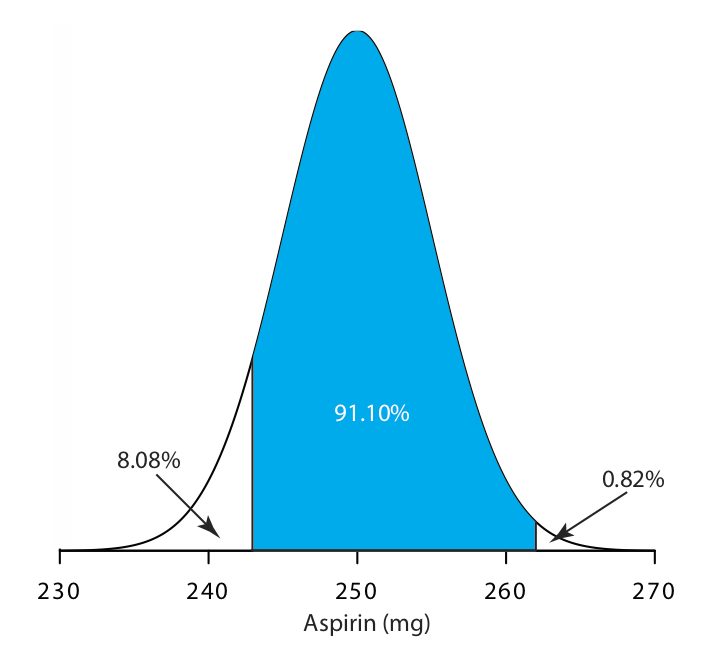
Це ділить нормальну криву розподілу на три області: область, яка відповідає нашій відповіді (показана синім кольором), область праворуч від цього і область зліва від цього. Обчисліть значення z для меж площі, яка відповідає вашій відповіді. Використовуйте таблицю, щоб знайти області праворуч і ліворуч від цих відхилень. Відніміть ці значення з 100% і, наприклад, у вас є відповідь.

Таблиця $\PageIndex{1}$ : Значення для одностороннього нормального розподілу
z	0.00	0,01	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09
0.0	0.5000	0,4960	0,4920	0,4880	0,4840	0.4801	0,4761	0,4721	0,4681	0,4641
0.1	0.4602	0,4562	0,4522	0,4483	0,4443	0,4404	0,4365	0,4325	0,4286	0,4247
0.2	0,4207	0,4168	0,4129	0,4090	0,4502	0,4013	0,3974	0,3396	0,3897	0,3859
0.3	0,3821	0,3783	0,3745	0,3707	0,3669	0,3632	0,3594	0,3557	0,3520	0,3483
0.4	0,3446	0,3409	0,3372	0,3336	0,3300	0,3264	0,3228	0,3192	0,3156	0,3121
0.5	0,3085	0,3050	0,3015	0,2981	0,2946	0,2912	0,2877	0,2843	0,2810	0,2776
0.6	0,2743	0,2709	0,2676	0,2643	0,2611	0,2578	0,2546	0,2514	0,2483	0,2451
0.7	0,2420	0,2389	0,2358	0,2327	0,2296	0,2266	0,2236	0,2206	0,2177	0,2148
0.8	0,2119	0,2090	0,2061	0,2033	0.2005	0,1977	0.1949	0,1922	0,1894	0,1867
0.9	0,1841	0,1814	0,178	0,1762	0,1736	0.1711	0,1685	0,1660	0,1635	0.1611
1.0	0.1587	0,1562	0,1539	0,1515	0.1492	0,1469	0,1446	0,1423	0.1401	0.1379
1.1	0,1357	0.1335	0,1314	0,1292	0,1271	0,1251	0.1230	0.1210	0,1190	0,1170
1.2	0.1151	0.1131	0.1112	0,1093	0,1075	0,1056	0,1038	0,1020	0.1003	0.0985
1.3	0.0968	0.0951	0.0934	0.0918	0.0901	0.0885	0.0869	0.0853	0.0838	0.0823
1.4	0.0808	0.0793	0.0778	0.0764	0.0749	0.0735	0.0721	0.0708	0.0694	0.0681
1.5	0.0668	0.0655	0.0643	0.0630	0.0618	0.0606	0.0594	0.0582	0.0571	0.0559
1.6	0.0548	0.0537	0.0526	0.0516	0.0505	0.0495	0.0485	0.0475	0.0465	0.0455
1.7	0.0466	0.0436	0.0427	0.0418	0.0409	0.0401	0.0392	0,0384	0.0375	0.0367
1.8	0.0359	0.0351	0.0344	0.0336	0.0329	0.0322	0.0314	0.0307	0.0301	0.0294
1.9	0.0287	0.0281	0.0274	0.0268	0.0262	0.0256	0.0250	0.0244	0.0239	0.0233
2.0	0.0228	0.0222	0.0217	0.0212	0.0207	0.0202	0.0197	0.0192	0.0188	0.0183
2.1	0.0179	0.0174	0.0170	0.0166	0.0162	0.0158	0.0154	0,0150	0.0146	0.0143
2.2	0.0139	0.0136	0.0132	0.0129	0,0125	0.0122	0.0119	0.0116	0.0113	0.0110
2.3	0,0107	0.0104	0.0102		0,00964		0,00914		0,00866
2.4	0,00820		0,00776		0,00734		0,00695		0,00657
2.5	0,00621		0,00587		0,00554		0,00523		0,00494
2.6	0,00466		0,00440		0,00415		0,00391		0,00368
2.7	0,00347		0,00326		0,00307		0,00289		0,00272
2.8	0,00256		0,00240		0,00226		0.00212		0,00199
2.9	0,00187		0,00175		0,00164		0,00154		0,00144
3.0	0,00135
3.1	0.000968
3.2	0.000687
3.3	0.000483
3.4	0.000337
3.5	0.000233
3.6	0.000159
3.7	0.000108
3.8	0.0000723
3.9	0,0000481
4.0	0,0000317