35.1: Оцінка аналітичних даних
- Page ID
- 27438
Матеріал у цьому додатку адаптований з підручника Chemometrics Using R, який доступний через LibreTexts за цим посиланням. Крім матеріалу тут, підручник містить інструкції про те, як використовувати статистичну мову програмування R для проведення розрахунків.
Типи даних
В основі будь-якого аналізу лежать дані. Іноді наші дані описують категорію, а іноді вони числові; іноді наші дані передають порядок, а іноді - ні; іноді наші дані мають абсолютне посилання, а іноді вони мають довільне посилання; і іноді наші дані набувають дискретних значень, а іноді вони набувають безперервних значень. Незалежно від його форми, коли ми збираємо дані, наша мета полягає в тому, щоб витягти з них інформацію, яка може допомогти нам вирішити проблему.
Способи опису даних
Якщо ми розглянемо, як описувати дані, то нам потрібні деякі дані, з якими ми можемо працювати. В ідеалі нам потрібні дані, які легко збирати та легко зрозуміти. Це також корисно, якщо ви можете зібрати подібні дані самостійно, щоб ви могли повторити те, що ми тут висвітлюємо. Проста система, яка відповідає цим критеріям, полягає в аналізі вмісту мішків M&Ms Хоча ця система може здатися тривіальною, майте на увазі, що повідомлення про відсоток жовтих M&Ms у мішку аналогічно повідомленню про концентрацію Cu 2 + у зразку руди або води: обидва виражають кількість аналіта, присутнього в одиниці його матриці.
На початку цієї глави ми визначили чотири контрастні способи опису даних: категоричний проти числового, впорядкований проти невпорядкованого, абсолютне посилання проти довільного посилання та дискретне проти безперервного. Щоб надати значення цим описовим термінам, розглянемо дані в таблиці\(\PageIndex{1}\), яка включає рік придбання та аналізу сумки, вага, вказану на упаковці, тип M & Ms, кількість жовтих M & Ms в сумці, відсоток M & Ms, які були червоними, загальна кількість M&Ms в сумці та їх відповідні ряди.
| ідентифікатор сумки | рік | вага (унція) | тип | номер жовтий | % червоний | Всього M&Ms | ранг (за підсумками) |
|---|---|---|---|---|---|---|---|
| a | 2006 | 1.74 | арахісу | 2 | 27.8 | 18 | шостий |
| б | 2006 | 1.74 | арахісу | 3 | 4.35 | 23 | четвертий |
| c | 2000 | 0,80 | рівнина | 1 | 22.7 | 22 | п'ятий |
| d | 2000 | 0,80 | рівнина | 5 | 20.8 | 24 | третій |
| е | 1994 | 10.0 | рівнина | 56 | 23,0 | 331 | другий |
| f | 1994 | 10.0 | рівнина | 63 | 21.9 | 333 | перший |
Записи в таблиці\(\PageIndex{1}\) упорядковані за стовпчиками та рядками. Перший рядок, який іноді називають рядком заголовка, визначає змінні, що складають дані. Кожен додатковий рядок є записом для одного зразка, а кожен запис у записі зразка надає інформацію про одну зі змінних; таким чином, дані в таблиці перераховують результат для кожної змінної та для кожного зразка.
Категоричні проти числових даних
Зі змінних, включених в Таблицю\(\PageIndex{1}\), деякі є категоріальними, а деякі числовими. Категорична змінна надає якісну інформацію, яку ми можемо використовувати для опису зразків відносно один одного, або яку ми можемо використовувати для організації зразків у групи (або категорії). Для даних у таблиці ідентифікатор мішка\(\PageIndex{1}\), тип та ранг є категоріальними змінними.
Числова змінна надає кількісну інформацію, яку ми можемо використовувати у значущому обчисленні; наприклад, ми можемо використовувати кількість жовтих M&Ms та загальну кількість M & Ms для обчислення нової змінної, яка повідомляє відсоток M&Ms, які є жовтими. Для даних у таблиці\(\PageIndex{1}\), рік, вага (унція), кількість жовтого,% червоного M&Ms та загальна кількість M & Ms є числовими змінними.
Ми також можемо використовувати числову змінну для призначення зразків групам. Наприклад, ми можемо розділити прості M&Ms у таблиці на\(\PageIndex{1}\) дві групи на основі ваги зразка. Однак те, що робить числову змінну цікавішою, полягає в тому, що ми можемо використовувати її для кількісних порівнянь між зразками; таким чином, ми можемо повідомити, що в 10-унційній сумці\(14.4 \times\) стільки ж простих M & Ms, скільки в мішку 0,8 унції.
\[\frac{333 + 331}{24 + 22} = \frac{664}{46} = 14.4 \nonumber \]
Хоча ми могли б класифікувати рік як категоріальну змінну - не необгрунтований вибір, оскільки він може служити корисним способом групування зразків - ми перераховуємо її тут як числову змінну, оскільки вона може служити корисною прогностичною змінною в регресійному аналізі. З іншого боку, ранг не є числовою змінною, навіть якщо ми перепишемо ряди як числівники - оскільки немає значущих обчислень, які ми можемо виконати за допомогою цієї змінної.
Номінальні проти порядкових даних
Категоричні змінні описуються як іменні або порядкові. Номінальна категорична змінна не передбачає певного порядку; порядкова категорична змінна, з іншого боку, передає значуще почуття порядку. Для категоріальних змінних у таблиці\(\PageIndex{1}\) ідентифікатор та тип bag є номінальними змінними, а ранг - порядковою змінною.
Співвідношення проти інтервальних даних
Числова змінна описується як відношення або інтервал залежно від того, чи має вона (відношення) або не має (інтервал) абсолютного посилання. Хоча ми можемо виконати значущі обчислення за допомогою будь-якої числової змінної, тип обчислення, який ми можемо виконати, залежить від того, чи мають значення змінної абсолютне посилання.
Числова змінна має абсолютне посилання, якщо вона має значущий нуль - тобто нуль, що означає виміряну кількість жодного - проти якого ми посилаємося на всі інші вимірювання цієї змінної. Для числових змінних у таблиці\(\PageIndex{1}\) вага (oz), число жовте,% червоне та загальне M&Ms є змінними співвідношення, оскільки кожна з них має значущий нуль; рік є змінною інтервалу, оскільки її масштаб посилається на довільний момент часу, 1 до н.е., а не на початок часу.
Для змінної коефіцієнта ми можемо зробити значущі абсолютні та відносні порівняння між двома результатами, але лише значущі абсолютні порівняння для змінної інтервалу. Наприклад, розглянемо зразок e, який був зібраний у 1994 році і має 331 M&Ms, і зразок d, який був зібраний у 2000 році і має 24 M&Ms. Ми можемо повідомити про значне абсолютне порівняння для обох змінних: зразок e на шість років старше зразка d, а зразок e має на 307 більше M & Ms, ніж зразок d може повідомити про значуще відносне порівняння загальної кількості M & MS - є
\[\frac{331}{24} = 13.8 \times \nonumber \]
стільки ж M & Ms у зразку e, як у зразку d, але ми не можемо повідомити про значуще відносне порівняння за рік, оскільки зразок, зібраний у 2000 році, не є
\[\frac{2000}{1994} = 1.003 \times \nonumber \]
старше зразка, зібраного в 1994 році.
Дискретні проти безперервних даних
Нарешті, деталізація числової змінної надає ще один спосіб опису наших даних. Наприклад, ми можемо описати числову змінну як дискретну або безперервну. Числова змінна є дискретною, якщо вона може приймати лише конкретні значення - зазвичай, але не завжди, ціле значення - між її межами; безперервна змінна може приймати будь-яке можливе значення в межах своїх меж. Для числових даних у таблиці\(\PageIndex{1}\), рік, число жовте та загальне M&Ms дискретні тим, що кожен обмежений цілими значеннями. Чисельні змінні вага (унція) і% червоного кольору, з іншого боку, є безперервними змінними. Зверніть увагу, що вага є безперервною змінною, навіть якщо пристрій, який ми використовуємо для вимірювання ваги, дає дискретні значення.
Візуалізація даних
Стара приказка про те, що «картинка коштує 1000 слів», може бути не універсально вірною, але вона вірна, коли мова йде про аналіз даних. Наприклад, хороша візуалізація даних дозволяє нам бачити закономірності та зв'язки, які менш очевидні, коли ми дивимось на дані, розташовані в таблиці, і це забезпечує потужний спосіб розповісти історію наших даних. Припустимо, ми хочемо вивчити склад 1,69 унцій (47,9 г) пакетів простих M&Ms. Ми отримуємо 30 мішків M&Ms (по десять з кожного з трьох магазинів) і видаляємо M&Ms з кожного пакета один за іншим, записуючи кількість синіх, коричневих, зелених, помаранчевих, червоних і жовтих M&Ms. M&Ms у перших п'яти цукерок, витягнутих з кожного мішка, і записують фактичну вагу нетто M & Ms в кожному мішку. Таблиця\(\PageIndex{2}\) узагальнює дані, зібрані на цих зразках. Ідентифікатор мішка визначає порядок, в якому мішки були відкриті та проаналізовані.
| сумка | магазин | блакитний | коричневий | зелений | помаранчевий | червоний | жовтий | жовтий_перший_п'ять | нетто_вага |
|---|---|---|---|---|---|---|---|---|---|
| 1 | CVS | 3 | 18 | 1 | 5 | 7 | 23 | 2 | 49.287 |
| 2 | CVS | 3 | 14 | 9 | 7 | 8 | 15 | 0 | 48.870 |
| 3 | Цільова | 4 | 14 | 5 | 10 | 10 | 16 | 1 | 51.250 |
| 4 | Крогер | 3 | 13 | 5 | 4 | 15 | 16 | 0 | 48.692 |
| 5 | Крогер | 3 | 16 | 5 | 7 | 8 | 18 | 1 | 48.777 |
| 6 | Крогер | 2 | 12 | 6 | 10 | 17 | 7 | 1 | 46.405 |
| 7 | CVS | 13 | 11 | 2 | 8 | 6 | 17 | 1 | 49.693 |
| 8 | CVS | 13 | 12 | 7 | 10 | 7 | 8 | 2 | 49.391 |
| 9 | Крогер | 6 | 17 | 5 | 4 | 8 | 16 | 1 | 48.196 |
| 10 | Крогер | 8 | 13 | 2 | 5 | 10 | 17 | 1 | 47.326 |
| 11 | Цільова | 9 | 20 | 1 | 4 | 12 | 13 | 3 | 50.974 |
| 12 | Цільова | 11 | 12 | 0 | 8 | 4 | 23 | 0 | 50.081 |
| 13 | CVS | 3 | 15 | 4 | 6 | 14 | 13 | 2 | 47.841 |
| 14 | Крогер | 4 | 17 | 5 | 6 | 14 | 10 | 2 | 48.377 |
| 15 | Крогер | 9 | 13 | 3 | 8 | 14 | 8 | 0 | 47.004 |
| 16 | CVS | 8 | 15 | 1 | 10 | 9 | 15 | 1 | 50.037 |
| 17 | CVS | 10 | 11 | 5 | 10 | 7 | 13 | 2 | 48.599 |
| 18 | Крогер | 1 | 17 | 6 | 7 | 11 | 14 | 1 | 48.625 |
| 19 | Цільова | 7 | 17 | 2 | 8 | 4 | 18 | 1 | 48.395 |
| 20 | Крогер | 9 | 13 | 1 | 8 | 7 | 22 | 1 | 51.730 |
| 21 | Цільова | 7 | 17 | 0 | 15 | 4 | 15 | 3 | 50.405 |
| 22 | CVS | 12 | 14 | 4 | 11 | 9 | 5 | 2 | 47.305 |
| 23 | Цільова | 9 | 19 | 0 | 5 | 12 | 12 | 0 | 49.477 |
| 24 | Цільова | 5 | 13 | 3 | 4 | 15 | 16 | 0 | 48.027 |
| 25 | CVS | 7 | 13 | 0 | 4 | 15 | 16 | 2 | 48.212 |
| 26 | Цільова | 6 | 15 | 1 | 13 | 10 | 14 | 1 | 51.682 |
| 27 | CVS | 5 | 17 | 6 | 4 | 8 | 19 | 1 | 50.802 |
| 28 | Крогер | 1 | 21 | 6 | 5 | 10 | 14 | 0 | 49.055 |
| 29 | Цільова | 4 | 12 | 6 | 5 | 13 | 14 | 2 | 46.577 |
| 30 | Цільова | 15 | 8 | 9 | 6 | 10 | 8 | 1 | 48.317 |
Зібравши наші дані, ми далі вивчаємо їх на предмет можливих проблем, таких як відсутні значення (Чи забули ми записати кількість коричневих M & Ms в будь-якому з наших зразків?) , для помилок, що вводяться, коли ми записували дані (Чи неправильно записана десяткова крапка для будь-якої з чистих ваг?) , або для незвичайних результатів (Це дійсно так, що ця сумка має тільки жовтий M & M?). Ми також вивчаємо наші дані, щоб виявити цікаві спостереження, які ми, можливо, забажаємо вивчити (Здається, що більшість ваги нетто більше, ніж вага нетто, вказана на окремих упаковках. Чому це може бути? Чи суттєва різниця?) Коли наш набір даних невеликий, ми зазвичай можемо виявити можливі проблеми та цікаві спостереження без особливих труднощів; однак для великого набору даних це стає проблемою. Замість того, щоб намагатися досліджувати окремі цінності, ми можемо подивитися на наші результати візуально. Хоча може бути важко знайти одну, непарну точку даних, коли нам доводиться індивідуально переглядати 1000 зразків, вона часто вискакує, коли ми дивимося на дані, використовуючи один або кілька підходів, які ми вивчимо в цьому розділі.
Точкові ділянки
Точковий графік відображає дані для однієї змінної, причому значення кожного зразка побудовано на осі x. Окремі точки організовані вздовж осі y з першим зразком внизу і останнім зразком вгорі. \(\PageIndex{1}\)На малюнку показаний точковий графік для кількості коричневих M & Ms у 30 мішках M & Ms з табл\(\PageIndex{2}\). Розподіл точок виглядає випадковим, оскільки немає кореляції між ідентифікатором вибірки та кількістю коричневих M & Ms. Ми були б здивовані, якби виявили, що точки були розташовані від нижнього лівого до верхнього правого, оскільки це означає, що порядок, в якому ми відкриваємо мішки, визначає, чи вони мають багато або кілька коричневих M & Ms.
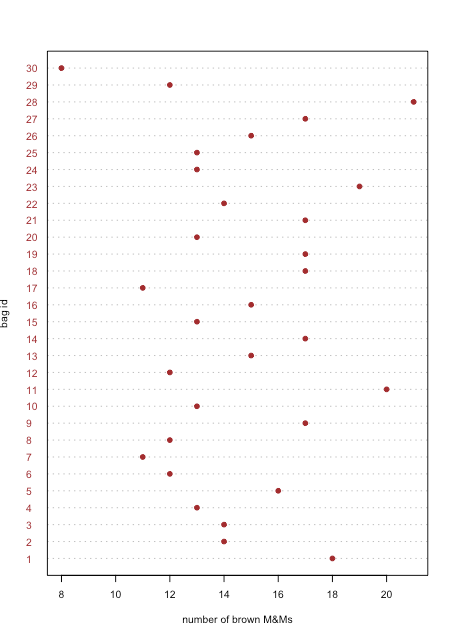
Стріп-діаграми
Точковий графік забезпечує швидкий спосіб дати нам впевненість у тому, що наші дані вільні від незвичайних закономірностей, але ціною простору, оскільки ми використовуємо вісь y, щоб включити ідентифікатор зразка як змінну. Stripchart використовує ту саму вісь x, як точковий графік, але не використовує вісь y для розрізнення зразків. Оскільки всі зразки з однаковою кількістю коричневих M & Ms з'являться в одному місці, що робить неможливим відрізнити їх один від одного, ми складаємо точки вертикально, щоб розкласти їх, як показано на малюнку\(\PageIndex{2}\).
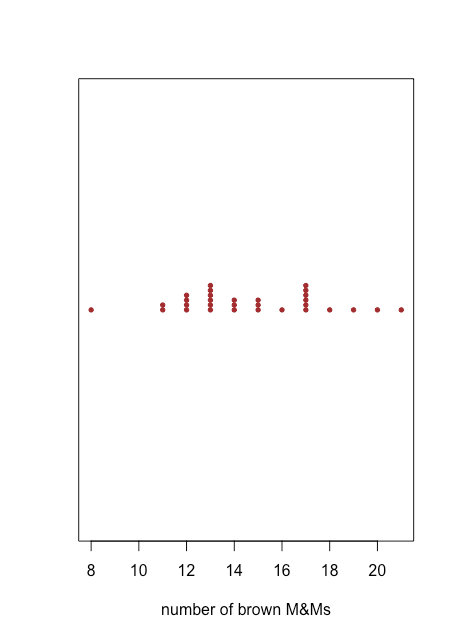
Як точковий графік на малюнку, так\(\PageIndex{1}\) і смугаста діаграма на малюнку\(\PageIndex{2}\) припускають, що існує менша щільність точок на нижній межі та верхня межа наших результатів. Ми бачимо, наприклад, що є лише одна сумка з 8, 16, 18, 19, 20 та 21 коричневим M&Ms, але є шість сумок з 13 та 17 коричневими M & Ms.
Оскільки stripchart не використовує вісь y для надання значущої категоріальної інформації, ми можемо легко відобразити кілька stripcharts одночасно. Рисунок\(\PageIndex{3}\) показує це для даних у табл\(\PageIndex{2}\). Замість того, щоб укладати окремі точки, ми перехитюємо їх, застосовуючи невелике випадкове зміщення до кожної точки. Серед речей, які ми дізнаємося з цієї смугової діаграми, є те, що лише коричневі та жовті M & Ms мають кількість більше 20 і що лише сині та зелені M & Ms мають кількість трьох або менше M & Ms.
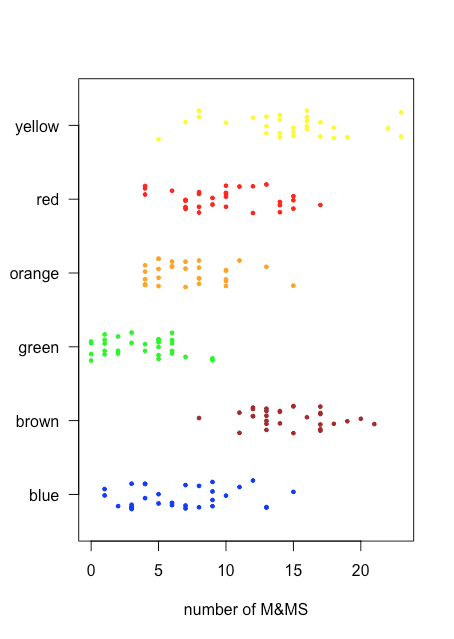
Коробка і вуса ділянки
Стріп-діаграму на малюнку нам\(\PageIndex{3}\) легко вивчити, оскільки кількість зразків, 30 мішків та кількість M & Ms на мішок досить мала, щоб ми могли бачити окремі точки. У міру того, як щільність точок стає більшою, смужкова діаграма стає менш корисною. Графік коробки та вусів забезпечує подібний вигляд, але фокусується на даних з точки зору діапазону значень, що охоплюють середні 50% даних.
\(\PageIndex{4}\)На малюнку показано графік коробки та вуса для коричневих M&Ms, використовуючи дані в табл\(\PageIndex{2}\). 30 окремих зразків накладаються як смугаста діаграма. Центральна коробка ділить вісь x на три області: мішки з менш ніж 13 коричневими M & Ms (сім зразків), мішки з 13 і 17 коричневими M & Ms (19 зразків) та мішки з більш ніж 17 коричневими M & Ms (чотири зразки). Обмеження коробки встановлені таким чином, щоб він включав принаймні середні 50% наших даних. У цьому випадку коробка містить 19 із 30 зразків (63%) мішків, оскільки переміщення будь-якого кінця коробки до середини призводить до коробки, яка включає менше 50% зразків. Різниця між верхньою межею коробки (19) та її нижньою межею (13) називається інтерквартильним діапазоном (IQR). Товста лінія в коробці - це медіана, або середнє значення (докладніше про це і IQR в наступному розділі). Пунктирні лінії в будь-якому кінці коробки називаються вусами, і вони поширюються на найбільший або найменший результат, який знаходиться в межах\(\pm 1.5 \times \text{IQR}\) правого або лівого краю коробки відповідно.
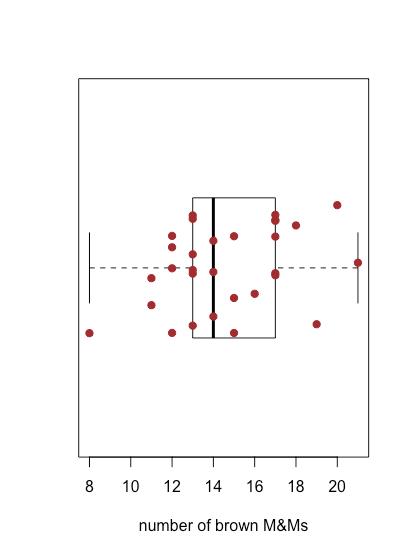
Оскільки графік коробки та вусів не використовує вісь y для надання значущої категоріальної інформації, ми можемо легко відобразити кілька графіків у одному кадрі. Рисунок\(\PageIndex{5}\) показує це для даних у табл\(\PageIndex{2}\). Зауважте, що коли значення потрапляє за межі вуса, як це відбувається тут для жовтих M & Ms, воно позначається відображенням його як відкритого кола.
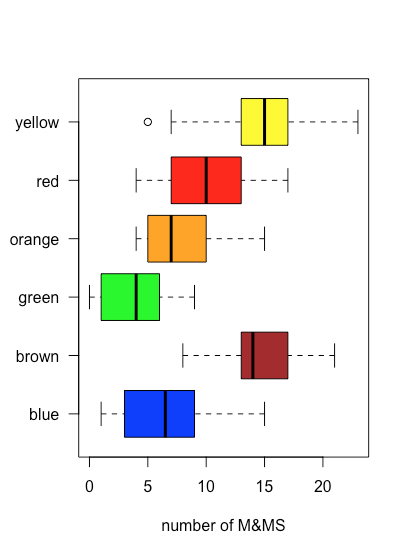
Одним із застосувань ділянки коробки та вусів є вивчення розподілу окремих зразків, особливо щодо симетрії. За винятком одиничного зразка, який потрапляє за межі вусів, розподіл жовтих M&Ms виглядає симетричним: медіана знаходиться поблизу центру коробки, а вуса простягаються однаково в обидві сторони. Розподіл помаранчевих M&Ms асиметричний: половина зразків має 4—7 M&Ms (лише чотири можливі результати), а половина - 7—15 M&Ms (дев'ять можливих результатів), що дозволяє припустити, що розподіл нахилений у бік більшої кількості помаранчевих M&Ms (див. Розділ 5 для отримання додаткової інформації про розподіл зразків).
\(\PageIndex{6}\)На малюнку показані ділянки коробки та вусів для жовтих M&Ms, згруповані відповідно до магазину, де були придбані мішки M&Ms. Хоча ділянки коробки та вусів досить різні з точки зору відносних розмірів коробок та відносної довжини вусів, точкові ділянки припускають, що розподіл базових даних відносно аналогічний тим, що більшість мішків містять 12-18 жовтих M & Ms і лише кілька мішків відхиляються від ці межі. Ці спостереження обнадіюють, оскільки ми не очікуємо, що вибір магазину вплине на склад мішків M&Ms. якби ми побачили докази того, що вибір магазину вплинув на наші результати, то ми б більш уважно подивилися на самі сумки для доказів погано контрольованої змінної, наприклад типу (Чи були ми випадково придбати пакетики арахісового масла M&Ms з одного магазину?) або номер партії товару (Чи змінив виробник склад кольорів між партіями?).
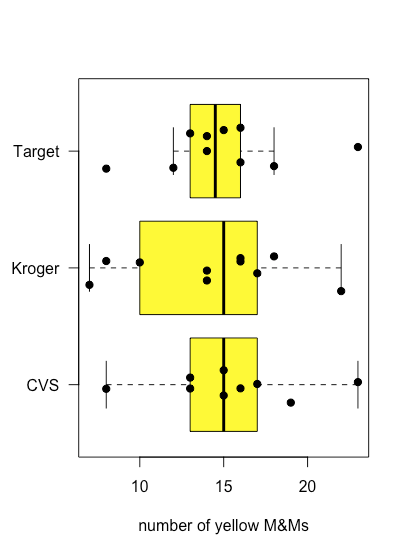
Барні ділянки
Хоча точковий графік, смугова діаграма та графік коробки та вуса дають деякі якісні докази того, як розподіляються значення змінної - нам доведеться більше сказати про розподіл даних у розділі 5 - вони менш корисні, коли нам потрібна більш кількісна картина розподілу. Для цього ми можемо використовувати смуговий графік, який відображає кількість кожного дискретного результату. \(\PageIndex{7}\)На малюнку показані штрихові графіки для помаранчевого та жовтого M&Ms, використовуючи дані в таблиці\(\PageIndex{2}\).
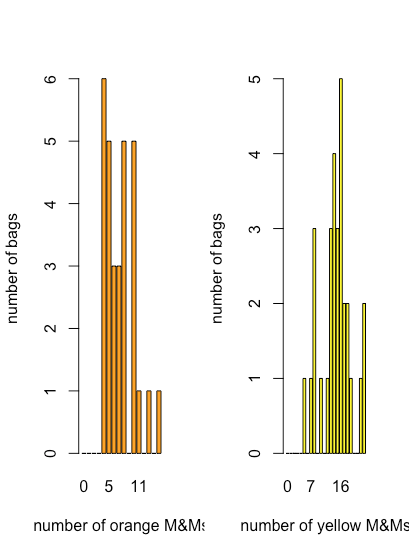
Тут ми бачимо, що найпоширеніша кількість помаранчевих M & Ms на мішок становить чотири, що також є найменшою кількістю помаранчевих M & Ms на мішок, і що спостерігається загальне зменшення кількості мішків у міру збільшення кількості помаранчевих M & M на мішок. Для жовтих M & Ms найпоширеніша кількість M & Ms на мішок становить 16, що падає поблизу середини діапазону жовтих M & Ms.
Гістограми
Графік смуги є корисним способом подивитися на розподіл дискретних результатів, таких як кількість помаранчевих або жовтих M&Ms, але це не корисно для безперервних даних, де кожен результат унікальний. Гістограма, в якій ми показуємо кількість результатів, які потрапляють у послідовність однаково розташованих контейнерів, забезпечує вигляд, подібний до вигляду штрихового графіка, але який працює з безперервними даними. На малюнку\(\PageIndex{8}\), наприклад, показана гістограма для чистих ваг 30 мішків M&Ms в табл\(\PageIndex{2}\). Окремі значення відображаються вертикальними хеш-мітками внизу гістограми.
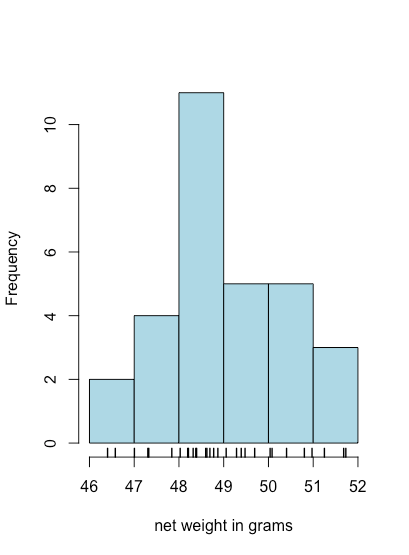
Узагальнення даних
В останньому розділі ми використовували дані, зібрані з 30 мішків M&Ms, для вивчення різних способів візуалізації даних. У цьому розділі ми розглянемо кілька способів узагальнення даних за допомогою ваги нетто тих самих мішків M&Ms. Ось необроблені дані.
| 49.287 | 48.870 | 51.250 | 48.692 | 48.777 | 46.405 |
| 49.693 | 49.391 | 48.196 | 47.326 | 50.974 | 50.081 |
| 47.841 | 48.377 | 47.004 | 50.037 | 48.599 | 48.625 |
| 48.395 | 51.730 | 50.405 | 47.305 | 49.477 | 48.027 |
| 48.212 | 51.682 | 50.802 | 49.055 | 46.577 | 48.317 |
Не виконуючи жодних розрахунків, які висновки ми можемо зробити, просто подивившись на ці дані? Ось кілька:
- Всі ваги нетто більше 46 г і менше 52 г.
- Як ми бачимо на малюнку\(\PageIndex{9}\), графік коробки та вуса (накладені смужковою діаграмою) та гістограма припускають, що розподіл ваг нетто є досить симетричним.
- Відсутність будь-яких точок за вусами ділянки «коробочка і вуса» говорить про те, що незвично великих або незвично дрібних ваг нетто немає.
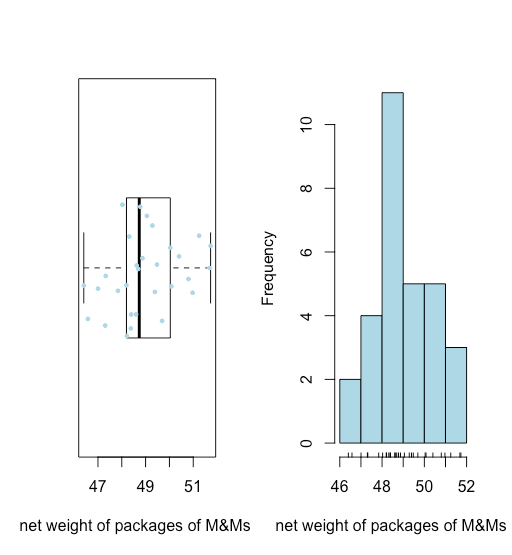
Обидві візуалізації забезпечують хорошу якісну картину даних, припускаючи, що окремі результати розкидані навколо якогось центрального значення з більшою кількістю результатів, ближче до того центрального значення, що на відстані від нього. Однак жодна візуалізація не описує дані кількісно. Нам потрібен зручний спосіб узагальнити дані, повідомляючи, де дані зосереджені та наскільки різноманітні індивідуальні результати навколо цього центру.
Де знаходиться Центр?
Існує два поширені способи звітування про центр набору даних: середній і медіанний.
Середнє,\(\overline{Y}\), - числове середнє, отримане шляхом складання результатів для всіх n спостережень і ділення на кількість спостережень
\[\overline{Y} = \frac{ \sum_{i = 1}^n Y_{i} } {n} = \frac{49.287 + 48.870 + \cdots + 48.317} {30} = 48.980 \text{ g} \nonumber \]
Медіана - це середнє значення після того\(\widetilde{Y}\), як ми замовляємо наші спостереження від найменшого до найбільшого, як ми показуємо тут для наших даних.
| 46.405 | 46.577 | 47.004 | 47.305 | 47.326 | 47.841 |
| 48.027 | 48.196 | 48.212 | 48.317 | 48.377 | 48.395 |
| 48.599 | 48.625 | 48.692 | 48.777 | 48.870 | 49.055 |
| 49.287 | 49.391 | 49.477 | 49.693 | 50.037 | 50.081 |
| 50.405 | 50.802 | 50.974 | 51.250 | 51.682 | 51.730 |
Якщо ми маємо непарну кількість зразків, то медіана - це просто середнє значення, або
\[\widetilde{Y} = Y_{\frac{n + 1}{2}} \nonumber \]
де n - кількість зразків. Якщо, як і тут, n парне, то
\[\widetilde{Y} = \frac {Y_{\frac{n}{2}} + Y_{\frac{n}{2}+1}} {2} = \frac {48.692 + 48.777}{2} = 48.734 \text{ g} \nonumber \]
Коли наші дані мають симетричний розподіл, як ми вважаємо тут, то середнє і медіана матимуть подібні значення.
Що таке варіація даних про центр?
Існує п'ять загальних заходів варіації даних про його центр: дисперсія, стандартне відхилення, діапазон, інтерквартильний діапазон та середнє середнє значення різниці.
Дисперсія, s 2, являє собою середнє квадратне відхилення окремих спостережень щодо середнього
\[s^{2} = \frac { \sum_{i = 1}^n \big(Y_{i} - \overline{Y} \big)^{2} } {n - 1} = \frac { \big(49.287 - 48.980\big)^{2} + \cdots + \big(48.317 - 48.980\big)^{2} } {30 - 1} = 2.052 \nonumber \]
і стандартне відхилення, s, - квадратний корінь дисперсії, що дає йому ті ж одиниці, що і середнє.
\[s = \sqrt{\frac { \sum_{i = 1}^n \big(Y_{i} - \overline{Y} \big)^{2} } {n - 1}} = \sqrt{\frac { \big(49.287 - 48.980\big)^{2} + \cdots + \big(48.317 - 48.980\big)^{2} } {30 - 1}} = 1.432 \nonumber \]
Діапазон w - це різниця між найбільшим і найменшим значенням в нашому наборі даних.
\[w = 51.730 \text{ g} - 46.405 \text{ g} = 5.325 \text{ g} \nonumber \]
Інтерквартильний діапазон, IQR, - це різниця між медіаною нижніх 25% спостережень та медіаною верхніх 25% спостережень; тобто він забезпечує міру діапазону значень, що охоплює середні 50% спостережень. Єдиної, стандартної формули розрахунку IQR не існує, а різні алгоритми дають дещо інші результати. Ми візьмемо описаний тут алгоритм:
1. Розділіть відсортований набір даних навпіл; якщо є непарна кількість значень, то видаліть медіану для повного набору даних. За нашими даними нижня половина
| 46.405 | 46.577 | 47.004 | 47.305 | 47.326 |
| 47.841 | 48.027 | 48.196 | 48.212 | 48.317 |
| 48.377 | 48.395 | 48.599 | 48.625 | 48.692 |
а верхня половина
| 48.777 | 48.870 | 49.055 | 49.287 | 49.391 |
| 49.477 | 49.693 | 50.037 | 50.081 | 50.405 |
| 50.802 | 50.974 | 51.250 | 51.682 | 51.730 |
2. Знайдіть F L, медіану для нижньої половини даних, яка для наших даних становить 48,196 г.
3. Знайдіть F U, медіану для верхньої половини даних, яка для наших даних становить 50.037 г.
4. IQR - це різниця між F U і F L.
\[F_{U} - F_{L} = 50.037 \text{ g} - 48.196 \text{ g} = 1.841 \text{ g} \nonumber \]
Медіана абсолютного відхилення, MAD, є медіаною абсолютних відхилень кожного спостереження від медіани всіх спостережень. Щоб знайти MAD для нашого набору 30 нетто ваг, спочатку віднімаємо медіану з кожного зразка в табл\(\PageIndex{3}\).
| 0,5525 | 0,135 | 2.5155 | -0.0425 | 0.0425 | -2.3295 |
| 0,9585 | 0,6565 | -0.5385 | -1.4085 | 2.2395 | 1,3465 |
| -0.8935 | -0.3575 | -1.7305 | 1,3025 | -0.1355 | -0.1095 |
| -0.3395 | 2.955 | 1.6705 | -1.4295 | 0,7425 | -0.7075 |
| -0.5225 | 2.9475 | 2.0675 | 0,3205 | -2.1575 | -0.4175 |
Далі беремо абсолютне значення кожної різниці і сортуємо їх від найменшого до великого.
| 0.0425 | 0.0425 | 0,1095 | 0,135 | 0,135 | 0,3205 |
| 0,3395 | 0,3575 | 0,4175 | 0,5225 | 0,5385 | 0,5525 |
| 0,6565 | 0,7075 | 0,7425 | 0.8935 | 0,9585 | 1,3025 |
| 1,3465 | 1,4085 | 1.4295 | 1.6705 | 1.7305 | 2.0675 |
| 2.1575 | 2.2395 | 2.3295 | 2.5155 | 2.9475 | 2.955 |
Нарешті, ми повідомляємо медіану для цих відсортованих значень як
\[\frac{0.7425 + 0.8935}{2} = 0.818 \nonumber \]
Робіцні проти неробастних заходів центру та варіації про центр
Хороше запитання полягає в тому, чому ми можемо захотіти більше одного способу повідомити про центр наших даних та зміну наших даних про центр. Припустимо, що результат для останнього з наших 30 зразків був повідомлений як 483.17 замість 48,317. Незалежно від того, чи це випадкове зміщення десяткової крапки чи справжній результат, не має значення для нас тут; важливо його вплив на те, що ми повідомляємо. Ось короткий виклад впливу цього одного значення на кожен з наших способів узагальнення наших даних.
| статистичні | оригінальні дані | нові дані |
|---|---|---|
| маю на увазі | 48.980 | 63.475 |
| медіана | 48.734 | 48.824 |
| дисперсія | 2.052 | 6285.938 |
| стандартне відхилення | 1.433 | 79.280 |
| діапазон | 5.325 | 436.765 |
| IQR | 1.841 | 1,885 |
| БОЖЕВІЛЬНИЙ | 0,818 | 0.926 |
Зверніть увагу, що середнє значення, дисперсія, стандартне відхилення та діапазон дуже чутливі до зміни останнього результату, але медіана, IQR та MAD - ні. Медіана, IQR та MAD вважаються надійною статистикою, оскільки вони менш чутливі до незвичайного результату; інші, звичайно, не надійні статистичні дані. Обидва типи статистики мають для нас цінність, до якої ми будемо повертатися час від часу.
Розподіл даних
Коли ми вимірюємо щось, наприклад відсоток жовтих M & Ms у мішку M&Ms, ми очікуємо двох речей:
- що існує основне «справжнє» значення, яке наші вимірювання повинні наблизити, і
- що результати індивідуальних вимірювань показуватимуть деяку зміну щодо цього «істинного» значення
Візуалізації даних, таких як точкові графіки, смугові діаграми, графіки коробки та вусів, гістограми, гістограми та розсіювачі, часто свідчать про наявність базової структури для наших даних. Наприклад, ми бачили, що розподіл жовтих M & Ms у мішках M & Ms більш-менш симетричний навколо його медіани, тоді як розподіл помаранчевих M & Ms був перекошений у бік більш високих значень. Ця основна структура або розподіл наших даних, оскільки вона впливає на те, як ми вирішимо аналізувати наші дані. У цьому розділі ми докладніше розглянемо кілька способів поширення даних.
Термінологія
Перш ніж розглядати різні типи дистрибутивів, давайте визначимося з деякими ключовими термінами. Ви також можете переглянути обговорення різних типів даних у розділі 2.
Популяції та зразки
Сукупність включає всі можливі вимірювання, які ми могли б зробити в системі, тоді як вибірка - це підмножина населення, на якій ми насправді проводимо вимірювання. Ці визначення є рідинними. Один мішок M&Ms - це населення, якщо нас цікавить лише ця конкретна сумка, але це лише один зразок з коробки, який містить брутто (144) окремих мішків. Ця коробка сама по собі може бути населенням, або це може бути один зразок з набагато більшої виробничої партії. І так далі.
Дискретні розподіли та безперервні розподіли
При дискретному розподілі можливі результати набувають обмеженого набору конкретних значень, які не залежать від того, як ми робимо наші вимірювання. Коли ми визначаємо кількість жовтих M & Ms в мішку, результати обмежуються цілими значеннями. Ми можемо знайти 13 жовтих M & Ms або 24 жовтих M & Ms, але ми не можемо отримати результат 15,43 жовтих M & Ms.
Для безперервного розподілу результат вимірювання може приймати будь-яке можливе значення між нижньою та верхньою межею, навіть якщо наш вимірювальний прилад має обмежену точність; таким чином, коли ми зважуємо мішок M&Ms на тризначному балансі і отримуємо результат 49,287 г, ми знаємо, що його справжня маса більше 49,2865... г і менше 49,2875... г.
Теоретичні моделі розподілу даних
Існує чотири важливі типи розподілів, які ми розглянемо в цьому розділі: рівномірний розподіл, біноміальний розподіл, розподіл Пуассона та нормальний, або Гауссоновий, розподіл. У попередніх розділах ми використовували аналіз мішків M&Ms для вивчення способів візуалізації даних та узагальнення даних. Тут ми будемо використовувати той самий набір даних для вивчення розподілу даних.
Рівномірний розподіл
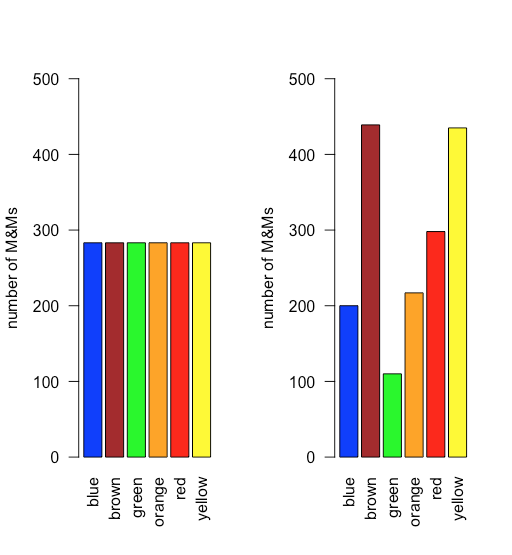
При рівномірному розподілі всі результати однаково вірогідні. Припустимо, населення M&Ms має рівномірний розподіл. Якщо це так, то з шістьма кольорами ми очікуємо, що кожен колір з'явиться з ймовірністю 1/6 або 16,7%. \(\PageIndex{10}\)На малюнку показано порівняння теоретичних результатів, якщо ми намалюємо 1699 M&Ms - загальна кількість M & Ms у нашій вибірці з 30 мішків - від популяції з рівномірним розподілом (зліва) до фактичного розподілу 1699 M&Ms у нашому зразку (праворуч). Здається малоймовірним, що населення M&Ms має рівномірний розподіл кольорів!
Біноміальний розподіл
Біноміальний розподіл показує ймовірність отримання певного результату у фіксованій кількості випробувань, де відомі шанси того результату, що відбувається в одному дослідженні. Математично біноміальний розподіл визначається рівнянням
\[P(X, N) = \frac {N!} {X! (N - X)!} \times p^{X} \times (1 - p)^{N - X} \nonumber \]
де P (X, N) - ймовірність того, що подія відбудеться X разів у N випробуваннях, а де p - ймовірність того, що подія відбудеться в одному дослідженні. Біноміальний розподіл має теоретичне середнє\(\mu\), і теоретичну\(\sigma^2\) дисперсію,
\[\mu = Np \quad \quad \quad \sigma^2 = Np(1 - p) \nonumber \]
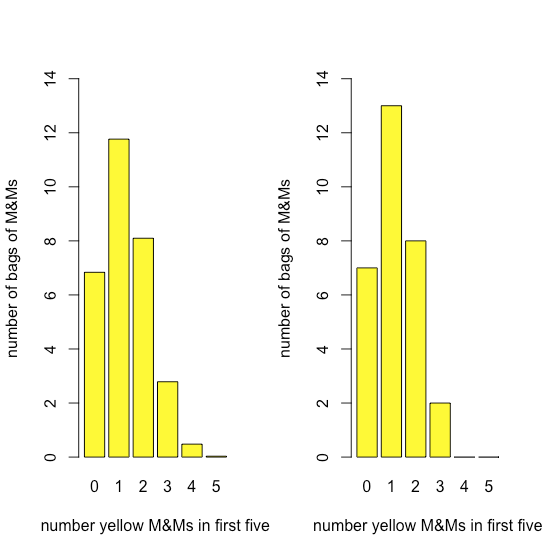
Рисунок\(\PageIndex{11}\) порівнює очікуваний біноміальний розподіл для малювання 0, 1, 2, 3, 4 або 5 жовтих M & Ms у перших п'яти M&MS - припускаючи, що ймовірність нанесення жовтого M & M становить 435/1699, співвідношення кількості жовтих M & Ms та загальної кількості M & MS - до фактичного розподілу результати. Подібність між теоретичними та фактичними результатами здається очевидною; в наступному розділі ми розглянемо способи перевірки цього твердження.
Розподіл Пуассона
Біноміальний розподіл корисний, якщо ми хочемо змоделювати ймовірність знаходження фіксованої кількості жовтих M & Ms у вибірці M & Ms фіксованого розміру - таких як перші п'ять M & Ms, які ми витягуємо з мішка, але не ймовірність знайти фіксовану кількість жовтих M & Ms в одній сумці, оскільки є деяка мінливість у загальній кількості M & Ms на мішок.
Розподіл Пуассона дає ймовірність того, що задана кількість подій відбудеться за фіксований проміжок часу або простору, якщо подія має відомий середній показник і якщо кожна нова подія не залежить від попередньої події. Математично розподіл Пуассона визначається рівнянням
\[P(X, \lambda) = \frac {e^{-\lambda} \lambda^X} {X !} \nonumber \]
де\(P(X, \lambda)\) - ймовірність того, що подія трапиться X разів, враховуючи середню швидкість події,\(\lambda\). Розподіл Пуассона має\(\mu\) теоретичне середнє значення та теоретичну дисперсію\(\sigma^2\), які кожен дорівнює\(\lambda\).
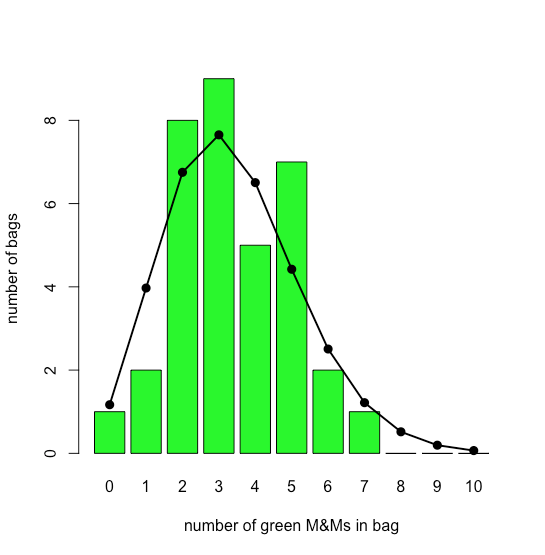
Графік бару на малюнку\(\PageIndex{12}\) показує фактичний розподіл зелених M & Ms у 35 маленьких мішках M&Ms (як повідомляє М.А. Сю-Фрідман «Ілюстрація концепцій квантового аналізу з інтуїтивною моделлю класу», адв. Physiol. Едук. 2013, 37, 112—116). На смугу накладається теоретичний розподіл Пуассона, заснований на їх повідомленій середній швидкості 3.4 зелених M & Ms за мішок. Подібність між теоретичними та фактичними результатами здається очевидною; у розділі 6 ми розглянемо способи перевірки цього твердження.
Нормальний розподіл
Рівномірний розподіл, біноміальний розподіл та розподіл Пуассона прогнозують ймовірність дискретної події, такої як ймовірність знаходження рівно двох зелених M&Ms у наступному мішку M&Ms, який ми відкриваємо. Не всі дані, які ми збираємо, є дискретними. Вага нетто мішків M&Ms є прикладом безперервних даних, оскільки маса окремого мішка не обмежується дискретним набором дозволених значень. У багатьох випадках ми можемо моделювати неперервні дані за допомогою нормального (або гаусового) розподілу, що дає ймовірність отримання певного результату, P (x), від популяції з відомим середнім значенням та відомою дисперсією\(\sigma^2\).\(\mu\) Математично нормальний розподіл визначається рівнянням
\[P(x) = \frac {1} {\sqrt{2 \pi \sigma^2}} e^{-(x - \mu)^2/(2 \sigma^2)} \nonumber \]
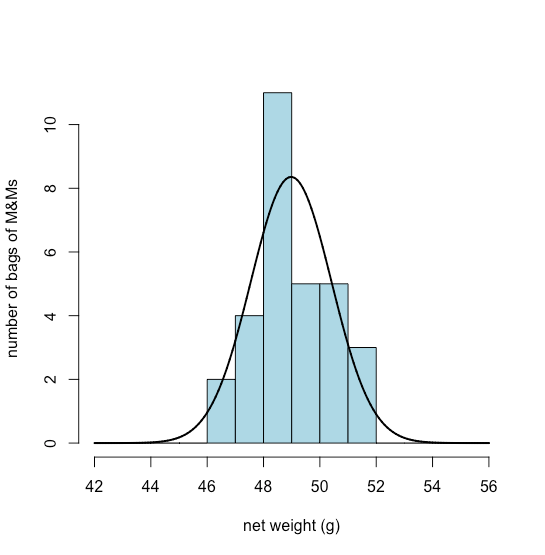
\(\PageIndex{13}\)На малюнку показано очікуваний нормальний розподіл ваги нетто нашої вибірки з 30 мішків M & Ms, якщо припустити\(\overline{X}\), що їх середнє значення 48,98 г і стандартне відхилення, с, 1.433 г є хорошими предикторами середнього показника популяції та стандартного відхилення,\(\mu\) \(\sigma\). Враховуючи невеликий зразок із 30 мішків, угода між моделлю та даними здається розумною.
Центральна гранична теорема
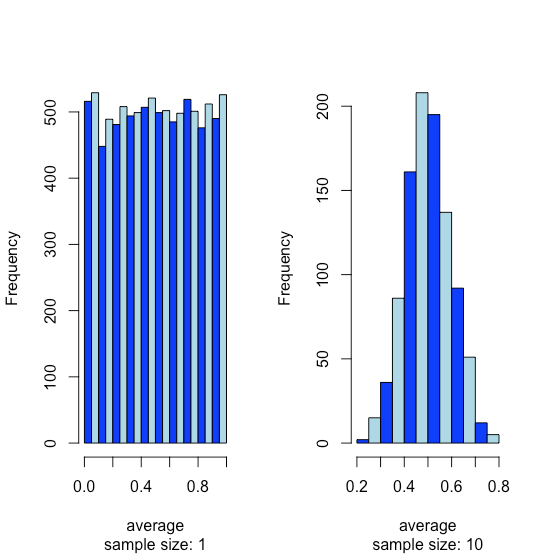
Припустимо, у нас є популяція, для якої одна з її властивостей має рівномірний розподіл, де кожен результат між 0 і 1 однаково вірогідний. Якщо ми проаналізуємо 10 000 зразків, ми не повинні дивуватися, виявивши, що розподіл цих 10000 результатів виглядає рівномірним, як показано гістограмою в лівій частині малюнка\(\PageIndex{14}\). Якщо ми збираємо 1000 об'єднаних зразків, кожен з яких складається з 10 окремих зразків для загальної кількості 10 000 окремих зразків - і повідомити про середні результати для цих 1000 об'єднаних зразків, ми побачимо щось цікаве, оскільки їх розподіл, як показано на гістограмі праворуч, виглядає чудово як нормальний дистрибутив. Коли ми малюємо окремі зразки з рівномірного розподілу, кожен можливий результат однаково вірогідний, тому ми бачимо розподіл ліворуч. Однак, коли ми малюємо об'єднаний зразок, який складається з 10 окремих зразків, середні значення, швидше за все, знаходяться поблизу середини діапазону розподілу, як ми бачимо праворуч, оскільки об'єднана вибірка, ймовірно, включає значення, отримані як з нижньої половини, так і з верхньої половини рівномірного розподілу. .
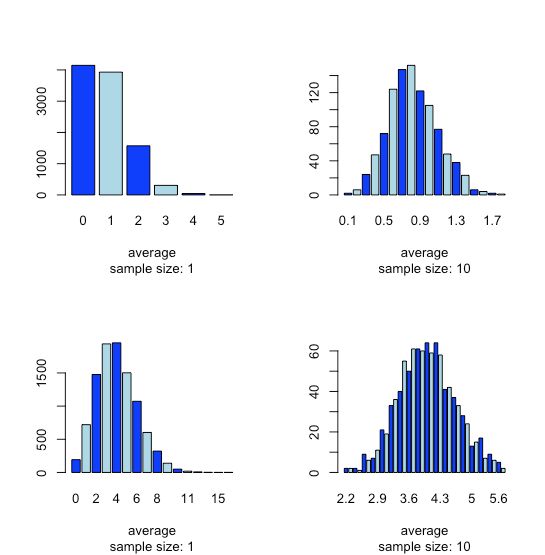
Ця тенденція до нормального розподілу виникає, коли ми об'єднуємо зразки, відома як центральна гранична теорема. Як показано на малюнку\(\PageIndex{15}\), ми бачимо подібний ефект з популяціями, які слідують за біноміальним розподілом або розподілом Пуассона.
Ви можете розумно запитати, чи важлива центральна гранична теорема, оскільки навряд чи ми виконаємо 1000 аналізів, кожен з яких є середнім показником 10 індивідуальних випробувань. Це обманює. Коли ми купуємо зразок грунту, наприклад, він складається з безлічі окремих частинок, кожна з яких є індивідуальним зразком грунту. Отже, наш аналіз цього зразка є середнім значенням для великої кількості окремих частинок ґрунту. Через це актуальна центральна гранична теорема.
Невизначеність даних
В останньому розділі ми розглянули чотири способи розподілу окремих зразків, які ми збираємо та аналізуємо, щодо центрального значення: рівномірний розподіл, біноміальний розподіл, розподіл Пуассона та нормальний розподіл. Ми також дізналися, що незалежно від того, як розподіляються окремі вибірки, розподіл середніх для декількох вибірок часто слідує нормальному розподілу. Ця тенденція до нормального розподілу виникає, коли ми повідомляємо середні значення для декількох зразків, відома як центральна гранична теорема. У цьому розділі ми більш уважно розглянемо нормальний розподіл - вивчаючи деякі його властивості, і розглянемо, як ми можемо використовувати ці властивості, щоб сказати щось більш значуще про наші дані, ніж просто повідомляти про середнє і стандартне відхилення.
Властивості нормального розподілу
Математично нормальний розподіл визначається рівнянням
\[P(x) = \frac {1} {\sqrt{2 \pi \sigma^2}} e^{-(x - \mu)^2/(2 \sigma^2)} \nonumber \]
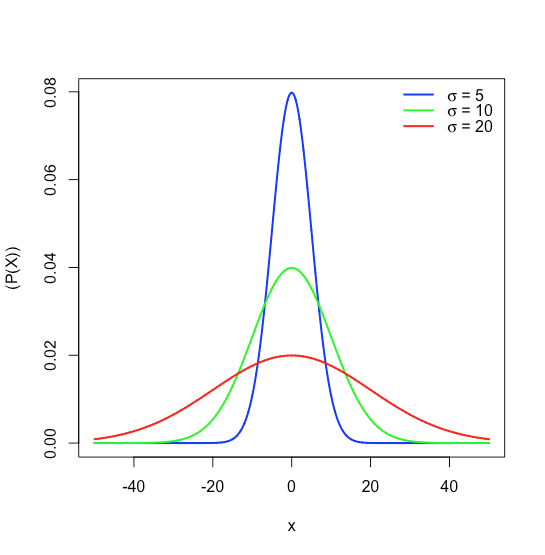
де\(P(x)\) - ймовірність отримання результату\(x\), від популяції з відомим середнім значенням\(\mu\), і відомим стандартним відхиленням,\(\sigma\). \(\PageIndex{16}\)На малюнку показані нормальні криві розподілу для\(\mu = 0\) стандартних відхилень 5, 10 і 20.
Оскільки рівняння для нормального розподілу залежить виключно від середнього значення популяції та її стандартного відхилення, ймовірність того\(\sigma\), що вибірка, отримана з популяції, має значення між будь-якими двома довільними межами, однакова для всіх популяцій.\(\mu\) Наприклад, малюнок\(\PageIndex{17}\) показує, що 68,26% всіх зразків, взятих із нормально розподіленої сукупності, мають значення в межах діапазону\(\mu \pm 1\sigma\), і лише 0,14% мають значення більше\(\mu + 3\sigma\).
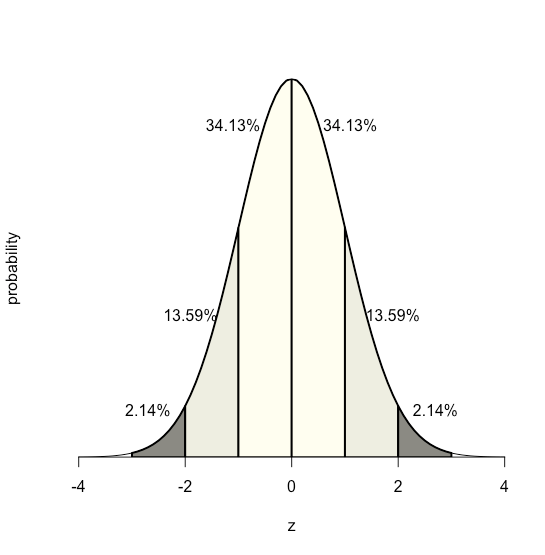
Ця особливість нормального розподілу - що площа під кривою однакова для всіх значень\(\sigma\) —дозволяє нам створити таблицю ймовірностей (див. Додаток 2) на основі відносного відхилення між межею, x та середнім значенням,\(\mu\).\(z\)
\[z = \frac {x - \mu} {\sigma} \nonumber \]
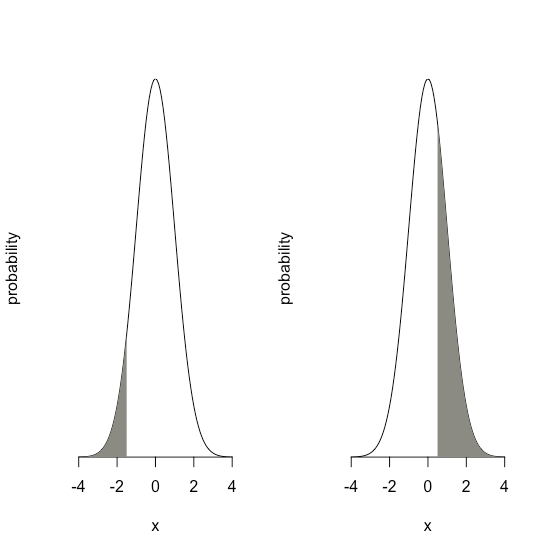
Значення\(z\) дає площу під кривою між цією межею та найближчим хвостом розподілу, як показано на малюнку\(\PageIndex{18}\).
Припустимо, ми знаємо, що\(\mu\) це 5.5833 ppb Pb і\(\sigma\) це 0.0558 ppb Pb для конкретного стандартного довідкового матеріалу (SRM). Яка ймовірність того, що ми отримаємо результат, який перевищує 5.650 ppb, якщо проаналізувати одну випадкову вибірку, взяту з SRM?
Рішення
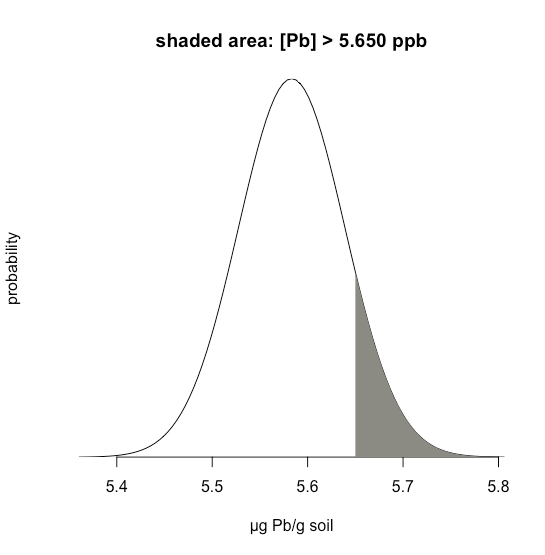
\(\PageIndex{19}\)На малюнку показана нормальна крива розподілу, задані значення 5,5833 ppb Pb для\(\mu\) і 0,0558 ppb Pb\(\sigma\). Затінена область на малюнках - це ймовірність отримання зразка з концентрацією Pb більше 5,650 проміле. Для визначення ймовірності спочатку обчислюємо\(z\)
\[z = \frac {x - \mu} {\sigma} = \frac {5.650 - 5.5833} {0.0558} = 1.195 \nonumber \]
Далі ми шукаємо ймовірність в Додатку 2 для цього значення\(z\), яке є середнім значенням 0.1170 (for\(z = 1.19\)) і 0.1151 (для\(z = 1.20\)), або ймовірність 0.1160; таким чином, ми очікуємо, що 11,60% зразків нададуть результат більше 5.650 ppb.
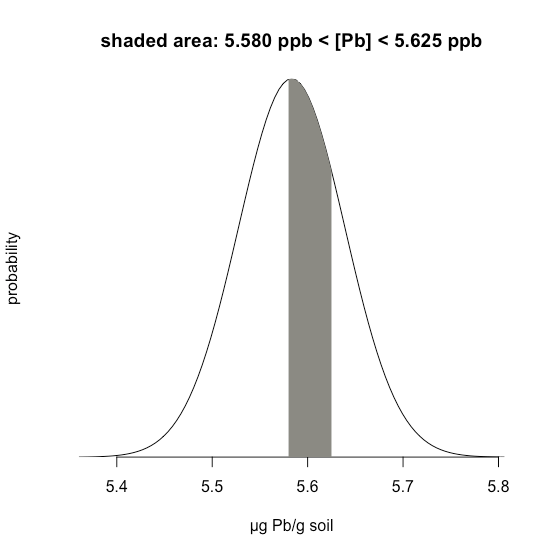
У прикладі\(\PageIndex{1}\) розглядається одна межа — ймовірність того, що результат перевищує одне значення. Але що робити, якщо ми хочемо визначити ймовірність того, що зразок має між 5,580 г Pb і 5.625 г Pb?
Рішення
В даному випадку нас цікавить затінена область, показана на малюнку\(\PageIndex{20}\). Спочатку розраховуємо\(z\) для верхньої межі
\[z = \frac {5.625 - 5.5833} {0.0558} = 0.747 \nonumber \]
а потім розраховуємо\(z\) для нижньої межі
\[z = \frac {5.580 - 5.5833} {0.0558} = -0.059 \nonumber \]
Потім ми шукаємо ймовірність у Додатку 2, що результат перевищить нашу верхню межу 5.625, що становить 0.2275, або 22,75%, і ймовірність того, що результат буде меншим за нашу нижню межу 5.580, що становить 0.4765, або 47,65%. Загальна незаштрихована площа становить 71,4% від загальної площі, тому затінена область відповідає ймовірності
\[100.00 - 22.75 - 47.65 = 100.00 - 71.40 = 29.6 \% \nonumber \]
Довірчі інтервали
У попередньому розділі ми навчилися прогнозувати ймовірність отримання того чи іншого результату, якщо наші дані нормально розподіляються з відомим\(\mu\) і відомим\(\sigma\). Наприклад, ми підрахували, що 11,60% зразків, взятих випадковим чином із стандартного еталонного матеріалу, матимуть концентрацію Pb більше 5,650 ppb, враховуючи 5,5833 ppb та a\(\sigma\) 0,0558 ppb.\(\mu\) По суті, ми визначили, від якої кількості стандартних відхилень становить 5,650,\(\mu\) і використали це для визначення ймовірності заданої стандартної площі при нормальній кривій розподілу.
Ми можемо поглянути на це по-іншому, задаючи наступне питання: Якщо ми збираємо одну вибірку навмання з популяції з відомим\(\mu\) і відомим\(\sigma\), в якому діапазоні значень ми можемо обґрунтовано очікувати, щоб знайти результат вибірки 95% часу? Перестановка рівняння
\[z = \frac {x - \mu} {\sigma} \nonumber \]
і рішення для\(x\) дарує
\[x = \mu \pm z \sigma = 5.5833 \pm (1.96)(0.0558) = 5.5833 \pm 0.1094 \nonumber \]
де a\(z\) 1,96 відповідає 95% площі під кривою; ми називаємо це 95% довірчим інтервалом для однієї вибірки.
Як правило, погано робити висновок з результату одного експерименту; натомість ми зазвичай збираємо кілька зразків і задаємо питання таким чином: якщо ми збираємо\(n\) випадкові зразки з популяції з відомим\(\mu\) і відомим\(\sigma\), в якому діапазоні значень ми могли б розумно розраховувати знайти середнє значення цих зразків 95% часу?
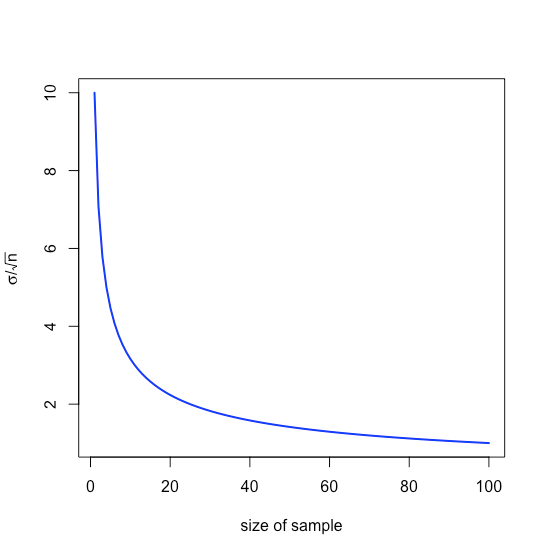
Ми можемо обґрунтовано очікувати, що стандартне відхилення для середнього значення декількох зразків менше, ніж стандартне відхилення для набору окремих зразків; насправді це так, і воно дається як
\[\sigma_{\bar{x}} = \frac {\sigma} {\sqrt{n}} \nonumber \]
де\(\frac {\sigma} {\sqrt{n}}\) називається стандартною похибкою середнього. Наприклад, якщо ми зберемо три зразки зі стандартного довідкового матеріалу, описаного вище, то ми очікуємо, що середнє значення для цих трьох зразків буде потрапляти в діапазон
\[\bar{x} = \mu \pm z \sigma_{\bar{X}} = \mu \pm \frac {z \sigma} {\sqrt{n}} = 5.5833 \pm \frac{(1.96)(0.0558)} {\sqrt{3}} = 5.5833 \pm 0.0631 \nonumber \]
тобто\(\pm 0.0631\) ppb навколо\(\mu\), діапазон, який менший, ніж у\(\pm 0.1094\) ppb, коли ми аналізуємо окремі зразки. Зверніть увагу, що відносне значення для нас збільшення розміру вибірки зменшується зі\(n\) збільшенням через квадратний кореневий термін, як показано на малюнку\(\PageIndex{21}\).
Наше лікування поки що передбачає, що ми знаємо\(\mu\) і\(\sigma\) для материнського населення, але ми рідко знаємо ці значення; натомість ми вивчаємо зразки, взяті з батьківської популяції,\(\bar{x}\) і задаємо наступне питання: Враховуючи середнє значення вибірки та її стандартне відхилення\(s\), що таке наше найкраща оцінка середнього чисельності населення\(\mu\), і його стандартного відхилення,\(\sigma\).
Щоб зробити цю оцінку, ми замінюємо стандартне відхилення населення\(\sigma\), на стандартне відхилення\(s\), для наших зразків, замінюємо середнє значення популяції\(\mu\), на середнє\(\bar{x}\), для наших зразків\(t\),\(z\) замінюємо на, де значення\(t\) залежить від кількість зразків,\(n\)
\[\bar{x} = \mu \pm \frac{ts}{\sqrt{n}} \nonumber \]
а потім переставити рівняння для вирішення\(\mu\).
\[\mu = \bar{x} \pm \frac {ts} {\sqrt{n}} \nonumber \]
Ми називаємо це довірчим інтервалом. Значення для\(t\) доступні в таблицях (див. Додаток 3) і залежать від рівня ймовірності\(\alpha\), де\((1 − \alpha) \times 100\) рівень довіри, і ступеня свободи\(n − 1\); зверніть увагу, що для будь-якого рівня ймовірності,\(t \longrightarrow z\) як\(n \longrightarrow \infty\).
Потрібно приділити особливу увагу тому, що означає цей довірчий інтервал і що він не означає:
- Це не означає, що існує 95% ймовірність того, що середнє значення населення знаходиться в діапазоні,\(\mu = \bar{x} \pm ts\) оскільки наші вимірювання можуть бути упередженими або нормальний розподіл може бути неприйнятним для нашої системи.
- Це забезпечує нашу найкращу оцінку середнього рівня популяції,\(\mu\) враховуючи наш аналіз\(n\) зразків, взятих випадковим чином з материнської популяції; однак інша вибірка дасть інший довірчий інтервал і, отже, іншу оцінку для\(\mu\).
Тестування значущості даних
Довірчий інтервал є корисним способом повідомити про результат аналізу, оскільки він встановлює обмеження на очікуваний результат. За відсутності детермінантної похибки або зміщення довірчий інтервал, заснований на середньому вибірці, вказує діапазон значень, в якому ми очікуємо знайти середнє значення популяції. Коли ми повідомляємо 95% довірчий інтервал для маси копійки як 3,117 г ± 0,047 г, наприклад, ми заявляємо, що існує лише 5% ймовірність того, що очікувана маса копійки менше 3,070 г або більше 3,164 г.
Оскільки довірчий інтервал - це твердження ймовірності, він дозволяє нам розглянути порівняльні питання, такі як:
«Чи значно відрізняються результати для недавно розробленого методу визначення холестерину в крові від отриманих стандартним методом?»
«Чи є значні зміни в складі дощової води, зібраної на різних ділянках за вітром від вугільної комунальної установки?»
У цьому розділі ми представляємо загальний підхід, який використовує експериментальні дані для задавання та відповіді на такі питання, підхід, який ми називаємо тестуванням значущості.
Надійність тестування значущості останнім часом приділяла велику увагу - див. Nuzzo, R. «Науковий метод: статистичні помилки», Nature, 2014, 506, 150-152 для загального обговорення питань - тому доцільно розпочати цю главу з відзначаючи необхідність забезпечення того, щоб наші дані та наше дослідження питання сумісні, так що ми не читаємо більше статистичного аналізу, ніж наші дані дозволяють; див. Leek, J. T; Peng, RD «Що таке питання? Наука, 2015, 347, 1314-1315 для корисного обговорення шести загальних дослідницьких питань.
У контексті аналітичної хімії тестування значущості часто супроводжує розвідувальний аналіз даних
«Чи є підстави підозрювати, що існує різниця між цими двома аналітичними методами при застосуванні до загальної вибірки?»
або аналіз інференційних даних.
«Чи є підстави підозрювати, що між цими двома незалежними вимірами існує взаємозв'язок?»
Статистично значущий результат для цих типів питань аналітичного дослідження, як правило, призводить до розробки додаткових експериментів, які краще підходять для прогнозування або пояснення основної причинно-наслідкової зв'язку. Тест на значущість - це перший крок до побудови більшого розуміння аналітичної проблеми, а не остаточної відповіді на цю проблему!
Тестування значущості
Розглянемо наступну проблему. Щоб визначити, чи ефективний препарат для зниження концентрації глюкози в крові, ми збираємо два набори зразків крові у пацієнта. Ми збираємо один набір зразків безпосередньо перед введенням ліків, а другий набір зразків збираємо через кілька годин. Після того, як ми проаналізуємо зразки, ми повідомляємо про їх відповідні засоби та відхилення. Як ми вирішуємо, чи успішно препарат знижував концентрацію глюкози в крові у пацієнта?
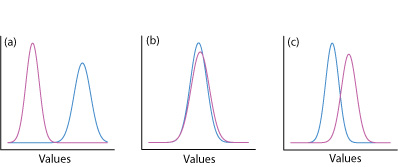
Одним із способів відповісти на це питання є побудова нормальної кривої розподілу для кожного зразка та порівняння двох кривих між собою. Три можливих результату показані на малюнку\(\PageIndex{22}\). На малюнку\(\PageIndex{22a}\) є повне поділ двох нормальних кривих розподілу, що говорить про те, що два зразки значно відрізняються один від одного. На малюнку\(\PageIndex{22b}\) нормальні криві розподілу для двох зразків майже повністю перекривають один одного, що говорить про те, що різниця між зразками незначна. Малюнок\(\PageIndex{22c}\), однак, ставить перед нами дилему. Хоча засоби для двох зразків здаються різними, перекриття їх нормальних кривих розподілу свідчить про те, що значна кількість можливих результатів може належати до будь-якого розподілу. У цьому випадку найкраще, що ми можемо зробити, - це зробити заяву про ймовірність того, що зразки значно відрізняються один від одного.
Процес, за допомогою якого ми визначаємо ймовірність того, що між двома зразками існує значна різниця, називається тестуванням значущості або тестуванням гіпотез. Перш ніж обговорити конкретні приклади, давайте спочатку встановимо загальний підхід до проведення та інтерпретації тесту на значущість.
Побудова тесту на значущість
Мета тесту на значущість - визначити, чи є різниця між двома або більше результатами достатньо великою, щоб нам було зручно заявити, що різниця не може бути пояснена невизначеними помилками. Першим кроком у побудові тесту на значущість є констатація проблеми як питання так чи ні, наприклад
«Чи ефективний цей препарат для зниження рівня глюкози в крові пацієнта?»
Нульова гіпотеза та альтернативна гіпотеза визначають дві можливі відповіді на наше запитання «так» чи «ні». Нульова гіпотеза, H 0, полягає в тому, що невизначені помилки достатні для пояснення будь-яких відмінностей між нашими результатами. Альтернативна гіпотеза H A полягає в тому, що відмінності в наших результатах занадто великі, щоб пояснюватися випадковою помилкою, і що вони повинні мати визначальний характер. Ми перевіряємо нульову гіпотезу, яку ми або зберігаємо, або відхиляємо. Якщо відкинути нульову гіпотезу, то треба прийняти альтернативну гіпотезу і зробити висновок, що різниця істотна.
Нездатність відхилити нульову гіпотезу - це не те саме, що прийняти її. Ми зберігаємо нульову гіпотезу, оскільки у нас недостатньо доказів, щоб довести її неправильну. Неможливо довести, що нульова гіпотеза вірна. Це важливий момент і той, який легко забути. Щоб оцінити цей момент, давайте використаємо ці дані для маси 100 циркулюючих копійок США.
| Пенні | Вага (г) | Пенні | Вага (г) | Пенні | Вага (г) | Пенні | Вага (г) |
|---|---|---|---|---|---|---|---|
| 1 | 3.126 | 26 | 3.073 | 51 | 3.101 | 76 | 3.086 |
| 2 | 3.140 | 27 | 3.084 | 52 | 3.049 | 77 | 3.123 |
| 3 | 3.092 | 28 | 3.148 | 53 | 3.082 | 78 | 3.15 |
| 4 | 3.095 | 29 | 3.047 | 54 | 3.142 | 79 | 3.055 |
| 5 | 3.080 | 30 | 3.121 | 55 | 3.082 | 80 | 3.057 |
| 6 | 3.065 | 31 | 3.116 | 56 | 3.066 | 81 | 3.097 |
| 7 | 3.117 | 32 | 3.005 | 57 | 3.128 | 82 | 3.066 |
| 8 | 3.034 | 33 | 3.15 | 58 | 3.112 | 83 | 3.113 |
| 9 | 3.126 | 34 | 3.103 | 59 | 3.085 | 84 | 3.102 |
| 10 | 3.057 | 35 | 3.086 | 60 | 3.086 | 85 | 3.033 |
| 11 | 3.053 | 36 | 3.103 | 61 | 3.084 | 86 | 3.112 |
| 12 | 3.099 | 37 | 3.049 | 62 | 3.104 | 87 | 3.103 |
| 13 | 3.065 | 38 | 2.998 | 63 | 3.107 | 88 | 3.198 |
| 14 | 3.059 | 39 | 3.063 | 64 | 3.093 | 89 | 3.103 |
| 15 | 3.068 | 40 | 3.055 | 65 | 3.126 | 90 | 3.126 |
| 16 | 3.060 | 41 | 3.181 | 66 | 3.138 | 91 | 3.111 |
| 17 | 3.078 | 42 | 3.108 | 67 | 3.131 | 92 | 3.126 |
| 18 | 3.125 | 43 | 3.114 | 68 | 3.120 | 93 | 3.052 |
| 19 | 3.090 | 44 | 3.121 | 69 | 3.100 | 94 | 3.113 |
| 20 | 3.100 | 45 | 3.105 | 70 | 3.099 | 95 | 3.085 |
| 21 | 3.055 | 46 | 3.078 | 71 | 3.097 | 96 | 3.117 |
| 22 | 3.105 | 47 | 3.147 | 72 | 3.091 | 97 | 3.142 |
| 23 | 3.063 | 48 | 3.104 | 73 | 3.077 | 98 | 3.031 |
| 24 | 3.083 | 49 | 3.146 | 74 | 3.178 | 99 | 3.083 |
| 25 | 3.065 | 50 | 3.095 | 75 | 3.054 | 100 | 3.104 |
Подивившись на дані, ми можемо запропонувати наступні нульові та альтернативні гіпотези.
H 0: Маса циркулюючого американського пенні становить від 2.900 г до 3.200 г
H A: Маса циркулюючої американської копійки може бути менше 2.900 г або більше 3.200 г
Для перевірки нульової гіпотези знаходимо копійку і визначаємо її масу. Якщо маса копійки дорівнює 2,512 г, то можна відкинути нульову гіпотезу і прийняти альтернативну гіпотезу. Припустимо, що маса копійки дорівнює 3.162 м Хоча цей результат підвищує нашу впевненість у нульовій гіпотезі, він не доводить, що нульова гіпотеза правильна, оскільки наступна копійка, яку ми вибірку, може важити менше 2.900 г або більше 3.200 г.
Після того, як ми викладемо null та альтернативні гіпотези, другим кроком є вибір рівня довіри для аналізу. Рівень довіри визначає ймовірність того, що ми неправильно відкинемо нульову гіпотезу, коли вона, по суті, істинна. Ми можемо висловити це як нашу впевненість у тому, що ми правильні у відкиданні нульової гіпотези (наприклад, 95%), або як ймовірність того, що ми неправильні у відхиленні нульової гіпотези. Для останніх рівень довіри дається як\(\alpha\), де
\[\alpha = 1 - \frac {\text{confidence interval (%)}} {100} \nonumber \]
Для 95% рівня довіри,\(\alpha\) це 0,05.
Третій крок - розрахувати відповідну статистику тесту і порівняти її з критичним значенням. Критичне значення тестової статистики визначає точку розриву між значеннями, які призводять нас до відхилення або збереження нульової гіпотези, яка є четвертим і останнім кроком тесту на значущість. Як ми побачимо в наступних розділах, як ми обчислюємо статистику тесту, залежить від того, що ми порівнюємо.
Чотири кроки для статистичного аналізу даних за допомогою тесту на значущість:
- Поставте питання і викласти нульову гіпотезу, H 0, і альтернативну гіпотезу, H A.
- Виберіть рівень довіри для статистичного аналізу.
- Розрахуйте відповідну статистику тесту і порівняйте її з критичним значенням.
- Або збережіть нульову гіпотезу, або відкиньте її і прийміть альтернативну гіпотезу.
Однохвостий і двохвіст значущості тести
Припустимо, ми хочемо оцінити точність нового аналітичного методу. Ми можемо використовувати цей метод для аналізу стандартного довідкового матеріалу, який містить відому концентрацію аналіту,\(\mu\). Ми аналізуємо стандарт кілька разів, отримуючи середнє значення\(\overline{X}\), для концентрації аналіта. Наша нульова гіпотеза полягає в тому, що немає різниці між\(\overline{X}\) і\(\mu\)
\[H_0 \text{: } \overline{X} = \mu \nonumber \]
Якщо ми проводимо тест на значущість\(\alpha = 0.05\), то ми зберігаємо нульову гіпотезу, якщо 95% довіри інтервал навколо\(\overline{X}\) містить\(\mu\). Якщо альтернативна гіпотеза
\[H_\text{A} \text{: } \overline{X} \neq \mu \nonumber \]
то відкидаємо нульову гіпотезу і приймаємо альтернативну гіпотезу, якщо\(\mu\) лежить в затінених областях в будь-якому кінці кривої розподілу ймовірності вибірки (рис.\(\PageIndex{23a}\)). На кожну з затінених областей припадає 2,5% площі під кривою розподілу ймовірностей, загалом 5%. Це двоххвостий тест на значущість, оскільки ми відхиляємо нульову гіпотезу для значень\(\mu\) на будь-якому екстремальному рівні кривої розподілу ймовірності вибірки.
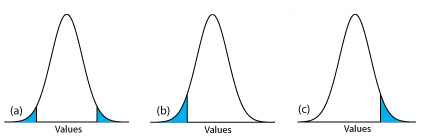
Ми можемо написати альтернативну гіпотезу двома додатковими способами
\[H_\text{A} \text{: } \overline{X} > \mu \nonumber \]
\[H_\text{A} \text{: } \overline{X} < \mu \nonumber \]
відхилення нульової гіпотези, якщо\(\mu\) потрапляє в затінені області\(\PageIndex{23c}\), показані на малюнку\(\PageIndex{23b}\) або малюнку відповідно. У кожному випадку затінена область становить 5% площі під кривою розподілу ймовірностей. Це приклади однохвостого тесту на значущість.
Для фіксованого рівня довіри тест на значення з двома хвостами є більш консервативним тестом, оскільки відкидання нульової гіпотези вимагає більшої різниці між результатами, які ми порівнюємо. У більшості ситуацій у нас немає особливих підстав очікувати, що один результат повинен бути більшим (або повинен бути меншим), ніж інший результат. Так відбувається, наприклад, коли ми оцінюємо точність нового аналітичного методу. Отже, двоххвостий тест на значущість, як правило, є відповідним вибором.
Ми залишаємо однохвостий тест на значущість для ситуації, коли ми конкретно зацікавлені в тому, чи один результат більший (або менший), ніж інший результат. Наприклад, однохвостий тест на значущість підходить, якщо ми оцінюємо здатність ліків знижувати рівень глюкози в крові. У цьому випадку нас цікавить лише те, чи рівень глюкози після введення препарату менше рівня глюкози до початку лікування. Якщо рівень глюкози в крові пацієнта більший після введення ліків, то ми знаємо відповідь - ліки не працювали - і нам не потрібно проводити статистичний аналіз.
Помилки при перевірці значущості
Оскільки тест на значущість спирається на ймовірність, його інтерпретація піддається помилці. У тесті на значущість\(\alpha\) визначає ймовірність відхилення нульової гіпотези, яка є істинною. Коли ми проводимо тест на значущість\(\alpha = 0.05\), існує 5% ймовірність того, що ми неправильно відхилимо нульову гіпотезу. Це відомо як помилка типу 1, і її ризик завжди еквівалентний\(\alpha\). Помилка типу 1 у двоххвостому або однохвостому тестах на значущість відповідає затіненим ділянкам під кривими розподілу ймовірностей на малюнку\(\PageIndex{23}\).
Другий тип помилки виникає, коли ми зберігаємо нульову гіпотезу, навіть якщо вона помилкова. Це помилка 2 типу, і ймовірність її виникнення є\(\beta\). На жаль, в більшості випадків ми не можемо обчислити або оцінити значення для\(\beta\). Імовірність помилки типу 2, однак, обернено пропорційна ймовірності помилки типу 1.
Мінімізація помилки типу 1 за рахунок зменшення\(\alpha\) збільшує ймовірність помилки типу 2. Коли ми вибираємо значення для\(\alpha\) ми повинні йти на компроміс між цими двома типами помилок. Більшість прикладів у цьому тексті використовують 95% рівня довіри (\(\alpha = 0.05\)), оскільки це зазвичай розумний компроміс між помилками типу 1 та 2 для аналітичної роботи. Однак незвично використовувати більш жорсткий (наприклад\(\alpha = 0.01\)) або більш м'який (наприклад\(\alpha = 0.10\)) рівень довіри, коли ситуація цього вимагає.
Тести значущості для нормальних розподілів
Звичайний розподіл - це найпоширеніший розподіл даних, які ми збираємо. Оскільки площа між будь-якими двома межами нормальної кривої розподілу чітко визначена, легко побудувати та оцінити тести на значущість.
Порівняння\(\overline{X}\) з\(\mu\)
Одним із способів перевірки нового аналітичного методу є аналіз зразка, який містить відому кількість аналіту,\(\mu\). Щоб судити про точність методу, ми аналізуємо кілька частин зразка, визначаємо середню кількість аналіту у зразку та використовуємо тест на значущість\(\overline{X}\) для порівняння\(\mu\).\(\overline{X}\) Нульова гіпотеза полягає в тому, що різниця між\(\overline{X}\) і\(\mu\) пояснюється невизначеними помилками, які впливають на наше визначення\(\overline{X}\). Альтернативна гіпотеза полягає в тому, що різниця між\(\overline{X}\) і\(\mu\) занадто велика, щоб пояснюватися невизначеною помилкою.
\[H_0 \text{: } \overline{X} = \mu \nonumber \]
\[H_A \text{: } \overline{X} \neq \mu \nonumber \]
Тестова статистика - t exp, яку ми підставляємо в довірчий інтервал для\(\mu\)
\[\mu = \overline{X} \pm \frac {t_\text{exp} s} {\sqrt{n}} \nonumber \]
Перевпорядкування цього рівняння і рішення для\(t_\text{exp}\)
\[t_\text{exp} = \frac {|\mu - \overline{X}| \sqrt{n}} {s} \nonumber \]
дає значення,\(t_\text{exp}\) коли\(\mu\) знаходиться на правому краю або на лівому краї довірчого інтервалу зразка (рис.\(\PageIndex{24a}\)).
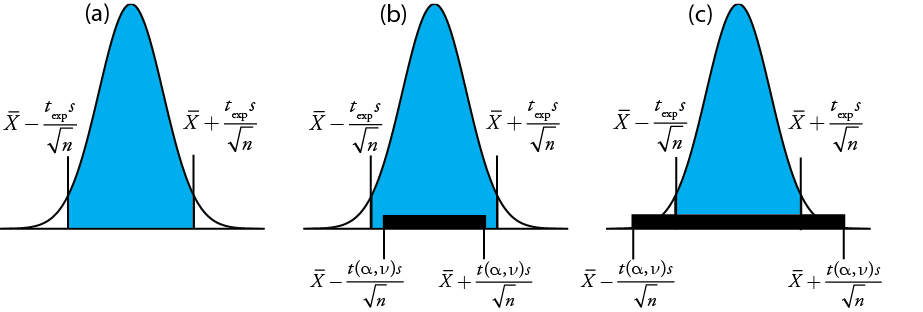
Щоб визначити, чи слід зберігати або відхиляти нульову гіпотезу, ми порівняємо значення t exp з критичним значенням\(t(\alpha, \nu)\), де\(\alpha\) рівень довіри та\(\nu\) ступені свободи для вибірки. Критичне значення\(t(\alpha, \nu)\) визначає найбільший довірчий інтервал, пояснений невизначеною помилкою. Якщо\(t_\text{exp} > t(\alpha, \nu)\), то довірчий інтервал нашої вибірки більше, ніж той, що пояснюється невизначеними помилками (рис.\(\PageIndex{24}\) b). У цьому випадку ми відкидаємо нульову гіпотезу і приймаємо альтернативну гіпотезу. Якщо\(t_\text{exp} \leq t(\alpha, \nu)\), то довірчий інтервал нашої вибірки менше, ніж пояснюється невизначеною помилкою, і ми зберігаємо нульову гіпотезу (рис.\(\PageIndex{24}\) С). Приклад\(\PageIndex{24}\) дає типове застосування цього тесту значущості, який відомий як t -тест\(\overline{X}\) to\(\mu\). Значення для ви знайдете\(t(\alpha, \nu)\) в Додатку 3.
Перш ніж визначити кількість Na 2 CO 3 в зразку, ви вирішили перевірити свою процедуру, проаналізувавши стандартний зразок, який становить 98,76% w/w Na 2 CO 3. П'ять реплікацій визначення% w/w Na 2 CO 3 в стандарті дають наступні результати
\(98.71 \% \quad 98.59 \% \quad 98.62 \% \quad 98.44 \% \quad 98.58 \%\)
Використовуючи\(\alpha = 0.05\), чи є якісь докази того, що аналіз дає неточні результати?
Рішення
Середнє і стандартне відхилення для п'яти випробувань
\[\overline{X} = 98.59 \quad \quad \quad s = 0.0973 \nonumber \]
Оскільки немає підстав вважати, що результати для стандарту повинні бути більшими або меншими\(\mu\), ніж, доречний двохвіст t -тест. Нульова гіпотеза та альтернативна гіпотеза
\[H_0 \text{: } \overline{X} = \mu \quad \quad \quad H_\text{A} \text{: } \overline{X} \neq \mu \nonumber \]
Тестова статистика, t exp, є
\[t_\text{exp} = \frac {|\mu - \overline{X}|\sqrt{n}} {2} = \frac {|98.76 - 98.59| \sqrt{5}} {0.0973} = 3.91 \nonumber \]
Критичне значення для t (0,05, 4) з додатка 3 - 2,78. Оскільки t exp більше t (0,05, 4), відкидаємо нульову гіпотезу і приймаємо альтернативну гіпотезу. На рівні довіри 95% різниця між\(\overline{X}\) і\(\mu\) є занадто великою, щоб пояснюватися невизначені джерела помилки, що говорить про наявність визначеного джерела помилки, що впливає на аналіз.
Є ще один спосіб інтерпретації результату цього t -тесту. Знаючи, що t exp дорівнює 3,91 і що існує 4 ступені свободи, ми використовуємо Додаток 3, щоб оцінити значення,\(\alpha\) яке відповідає t (\(\alpha\), 4) з 3.91. З додатка 3, т (0,02, 4) дорівнює 3,75, а т (0,01, 4) дорівнює 4,60. Хоча ми можемо відхилити нульову гіпотезу на рівні довіри 98%, ми не можемо відхилити її на рівні довіри 99%. Для обговорення переваг цього підходу див. Дж. С. Стерн і Г.Д. Сміт «Просіювання доказів - що не так з тестами значущості?» БМЖ 2001, 322, 226—231.
Раніше ми говорили про те, що ми повинні проявляти обережність, інтерпретуючи результат статистичного аналізу. Ми будемо продовжувати повертатися до цього моменту, оскільки це важливий. Визначивши, що результат неточний, як ми це робили в прикладі\(\PageIndex{3}\), наступним кроком є виявлення і виправлення помилки. Однак перш ніж витрачати час і гроші на це, ми спочатку повинні критично вивчити наші дані. Наприклад, чим менше значення s, тим більше значення t exp. Якщо стандартне відхилення для нашого аналізу нереально мало, то ймовірність помилки 2 типу зростає. Включення декількох додаткових повторюваних аналізів стандарту та переоцінка t -тесту може посилити наші докази щодо визначеної помилки, або це може показати нам, що немає доказів для визначеної помилки.
Порівняння\(s^2\) з\(\sigma^2\)
Якщо ми регулярно аналізуємо певну вибірку, ми можемо встановити очікувану дисперсію для аналізу.\(\sigma^2\) Це часто трапляється, наприклад, у клінічній лабораторії, яка щодня аналізує сотні зразків крові. Кілька повторюваних аналізів одного зразка дають дисперсію зразка, s 2, значення якої може або не може суттєво відрізнятися від\(\sigma^2\).
Ми можемо використовувати F -тест, щоб оцінити, чи є різниця між s 2 і\(\sigma^2\) є значною. Нульова гіпотеза є\(H_0 \text{: } s^2 = \sigma^2\) і альтернативна гіпотеза є\(H_\text{A} \text{: } s^2 \neq \sigma^2\). Тестова статистика для оцінки нульової гіпотези - F exp, яка дається як
\[F_\text{exp} = \frac {s^2} {\sigma^2} \text{ if } s^2 > \sigma^2 \text{ or } F_\text{exp} = \frac {\sigma^2} {s^2} \text{ if } \sigma^2 > s^2 \nonumber \]
в залежності від того, чи є s 2 більше або менше, ніж\(\sigma^2\). Цей спосіб визначення F exp гарантує, що його значення завжди більше або дорівнює одиниці.
Якщо нульова гіпотеза вірна, то F exp повинна дорівнювати одиниці; однак через невизначені помилки F exp, як правило, більше одиниці. Критичне значення є найбільшим значенням F exp\(F(\alpha, \nu_\text{num}, \nu_\text{den})\), яке ми можемо віднести до невизначеної помилки\(\alpha\), враховуючи заданий рівень значущості, і ступені свободи для дисперсії в чисельнику\(\nu_\text{num}\), і дисперсія в знаменнику,\(\nu_\text{den}\). Ступінь свободи для s 2 дорівнює n — 1, де n - кількість реплікацій, що використовуються для визначення дисперсії вибірки, а ступінь свободи для\(\sigma^2\) визначається як нескінченність,\(\infty\). Критичні значення F для\(\alpha = 0.05\) перераховані в Додатку 4 як для однохвостих, так і для двохвостих F -тестів.
Процес виробника для аналізу таблеток аспірину має відому дисперсію 25. Вибірка з 10 таблеток аспірину відбирається і аналізується на кількість аспірину, даючи наступні результати в мг аспірину/таблетці.
\(254 \quad 249 \quad 252 \quad 252 \quad 249 \quad 249 \quad 250 \quad 247 \quad 251 \quad 252\)
Визначте, чи є докази значної різниці між дисперсією вибірки та очікуваною дисперсією при\(\alpha = 0.05\).
Рішення
Дисперсія для проби 10 таблеток становить 4,3. Нульова гіпотеза та альтернативні гіпотези
\[H_0 \text{: } s^2 = \sigma^2 \quad \quad \quad H_\text{A} \text{: } s^2 \neq \sigma^2 \nonumber \]
і значення для F exp дорівнює
\[F_\text{exp} = \frac {\sigma^2} {s^2} = \frac {25} {4.3} = 5.8 \nonumber \]
Критичне значення для F (0,05,\(\infty\), 9) з додатка 4 - 3,333. Оскільки F exp більше F (0,05,, 9)\(\infty\), ми відкидаємо нульову гіпотезу і приймаємо альтернативну гіпотезу про те, що існує значна різниця між дисперсією вибірки та очікуваною дисперсією. Одним з пояснень різниці може бути те, що таблетки аспірину не були обрані випадковим чином.
Порівняння відхилень для двох зразків
Ми можемо розширити F -тест, щоб порівняти дисперсії для двох зразків, A і B, переписавши наше рівняння для F exp як
\[F_\text{exp} = \frac {s_A^2} {s_B^2} \nonumber \]
визначення A і B таким чином, щоб значення F exp було більше або дорівнювало 1.
У таблиці нижче наведені результати двох експериментів з визначення маси циркулюючої американської пенні. Визначте, чи є різниця в дисперсіях цих аналізів на\(\alpha = 0.05\).
| Перший експеримент | Другий експеримент | ||
|---|---|---|---|
| Пенні | Маса (г) | Пенні | Маса (г) |
| 1 | 3.080 | 1 | 3.052 |
| 2 | 3.094 | 2 | 3.141 |
| 3 | 3.107 | 3 | 3.083 |
| 4 | 3.056 | 4 | 3.083 |
| 5 | 3.112 | 5 | 3.048 |
| 6 | 3.174 | ||
| 7 | 3.198 | ||
Рішення
Стандартні відхилення для двох експериментів складають 0,051 для першого експерименту (А) і 0,037 для другого експерименту (B). Нульова та альтернативна гіпотези
\[H_0 \text{: } s_A^2 = s_B^2 \quad \quad \quad H_\text{A} \text{: } s_A^2 \neq s_B^2 \nonumber \]
і значення F exp дорівнює
\[F_\text{exp} = \frac {s_A^2} {s_B^2} = \frac {(0.051)^2} {(0.037)^2} = \frac {0.00260} {0.00137} = 1.90 \nonumber \]
З Додатка 4 критичне значення для F (0,05, 6, 4) дорівнює 9.197. Оскільки F exp < F (0,05, 6, 4), ми зберігаємо нульову гіпотезу. Немає жодних доказів,\(\alpha = 0.05\) щоб припустити, що різниця в дисперсіях є значною.
Порівняння засобів для двох зразків
На результат аналізу впливають три фактори: метод, вибірка та аналітик. Ми можемо вивчити вплив цих факторів, проводячи експерименти, в яких ми змінюємо один фактор, утримуючи постійними інші фактори. Наприклад, для порівняння двох аналітичних методів ми можемо мати одного і того ж аналітика застосувати кожен метод до одного і того ж зразка, а потім вивчити отримані кошти. Подібним чином ми можемо розробляти експерименти для порівняння двох аналітиків або порівняння двох зразків.
Перш ніж розглядати тести на значущість для порівняння засобів двох вибірок, нам потрібно зрозуміти різницю між непарними даними і парними даними. Це критична відмінність, і важливо навчитися розрізняти ці два типи даних. Ось два простих приклади, які підкреслюють різницю між непарними даними та парними даними. У кожному прикладі мета полягає в тому, щоб порівняти два залишки, зважуючи копійки.
- Приклад 1: Ми збираємо 10 копійок і зважуємо кожну копійку на кожному балансі. Це приклад парних даних, оскільки ми використовуємо ті ж 10 копійок для оцінки кожного балансу.
- Приклад 2: Ми збираємо 10 копійок і ділимо їх на дві групи по п'ять копійок кожна. Зважуємо копійки в першій групі на одному балансі і зважуємо другу групу копійок на іншому балансі. Зверніть увагу, що жодна копійка не зважується на обох залишках. Це приклад непарних даних, оскільки ми оцінюємо кожен баланс, використовуючи різну вибірку копійок.
В обох прикладах вибірки 10 копійок були взяті з однієї і тієї ж популяції; різниця полягає в тому, як ми відбирали цю популяцію. Ми дізнаємося, чому ця відмінність важлива, коли ми переглядаємо тест на значущість для парних даних; однак спочатку ми представляємо тест на значущість для непарних даних.
Один простий тест для визначення того, чи є дані парними або непарними, - це подивитися на розмір кожної вибірки. Якщо зразки мають різний розмір, то дані повинні бути непарними. Зворотне не відповідає дійсності. Якщо два зразки однакового розміру, вони можуть бути парними або непарними.
Непарні дані
Розглянемо два аналізи, A і B, із засобами\(\overline{X}_A\) і\(\overline{X}_B\), і стандартні відхилення s A і s B. Довірчі інтервали для\(\mu_A\) і\(\mu_B\) для
\[\mu_A = \overline{X}_A \pm \frac {t s_A} {\sqrt{n_A}} \nonumber \]
\[\mu_B = \overline{X}_B \pm \frac {t s_B} {\sqrt{n_B}} \nonumber \]
де n A і n B - розміри вибірки для A і для B. Наша нульова гіпотеза полягає в тому\(H_0 \text{: } \mu_A = \mu_B\), що будь-яка різниця між\(\mu_A\) і\(\mu_B\) є результатом невизначеної помилки, які впливають на аналіз. Альтернативна гіпотеза полягає в тому\(H_A \text{: } \mu_A \neq \mu_B\), що різниця між\(\mu_A\) і\(\mu_B\) занадто велика, щоб пояснюватися невизначеною помилкою.
Щоб вивести рівняння для t exp, ми вважаємо, що\(\mu_A\) дорівнює\(\mu_B\), і об'єднаємо рівняння для двох довірчих інтервалів
\[\overline{X}_A \pm \frac {t_\text{exp} s_A} {\sqrt{n_A}} = \overline{X}_B \pm \frac {t_\text{exp} s_B} {\sqrt{n_B}} \nonumber \]
Розв'язування\(|\overline{X}_A - \overline{X}_B|\) та використання поширення невизначеності, дає
\[|\overline{X}_A - \overline{X}_B| = t_\text{exp} \times \sqrt{\frac {s_A^2} {n_A} + \frac {s_B^2} {n_B}} \nonumber \]
Нарешті, ми вирішуємо для t exp
\[t_\text{exp} = \frac {|\overline{X}_A - \overline{X}_B|} {\sqrt{\frac {s_A^2} {n_A} + \frac {s_B^2} {n_B}}} \nonumber \]
і порівняти його з критичним значенням\(t(\alpha, \nu)\), де\(\alpha\) ймовірність помилки типу 1, а\(\nu\) це ступені свободи.
Поки що наша розробка цього t -тесту схожа на те, що\(\overline{X}\) для порівняння з\(\mu\), і все ж ми не маємо достатньої інформації для оцінки t -тесту. Бачите проблему? З двома незалежними наборами даних незрозуміло, скільки ступенів свободи ми маємо.
Припустимо, що\(s_A^2\)\(s_B^2\) розбіжності і дають оцінки однакові\(\sigma^2\). У цьому випадку ми можемо замінити\(s_A^2\) і\(s_B^2\) з об'єднаною дисперсією\(s_\text{pool}^2\), що є кращою оцінкою для дисперсії. Таким чином, наше рівняння для\(t_\text{exp}\) стає
\[t_\text{exp} = \frac {|\overline{X}_A - \overline{X}_B|} {s_\text{pool} \times \sqrt{\frac {1} {n_A} + \frac {1} {n_B}}} = \frac {|\overline{X}_A - \overline{X}_B|} {s_\text{pool}} \times \sqrt{\frac {n_A n_B} {n_A + n_B}} \nonumber \]
де басейн, об'єднане стандартне відхилення, є
\[s_\text{pool} = \sqrt{\frac {(n_A - 1) s_A^2 + (n_B - 1)s_B^2} {n_A + n_B - 2}} \nonumber \]
Знаменник цього рівняння показує нам, що ступені свободи для об'єднаного стандартного відхилення є\(n_A + n_B - 2\), яке також є ступенями свободи для t -тесту. Зверніть увагу, що ми втрачаємо два ступені свободи, тому що розрахунки для\(s_A^2\) і\(s_B^2\) вимагають попереднього розрахунку\(\overline{X}_A\) амд\(\overline{X}_B\).
Отже, як ви визначаєте, якщо це нормально, щоб об'єднати дисперсії? Використовуйте F-тест.
Якщо\(s_A^2\) і значно\(s_B^2\) відрізняються, то обчислюємо t exp, використовуючи наступне рівняння. У цьому випадку ми знаходимо ступені свободи, використовуючи наступне нав'язуюче рівняння.
\[\nu = \frac {\left( \frac {s_A^2} {n_A} + \frac {s_B^2} {n_B} \right)^2} {\frac {\left( \frac {s_A^2} {n_A} \right)^2} {n_A + 1} + \frac {\left( \frac {s_B^2} {n_B} \right)^2} {n_B + 1}} - 2 \nonumber \]
Оскільки ступені свободи повинні бути цілим числом, ми округляємо до найближчого цілого числа значення\(\nu\) отриманого з цього рівняння.
Рівняння вище для ступенів свободи взято з Міллера, J.C.; Міллер, J.N. статистика аналітичної хімії, 2-е видання, Елліс-Хорвард: Чичестер, Великобританія, 1988. У 6-му виданні автори відзначають, що запропоновано кілька різних рівнянь для числа ступенів свободи для t, коли s A і s B відрізняються, відображаючи той факт, що визначення ступенів свободи і наближення. Альтернативним рівнянням, яке використовується статистичними програмними пакетами, такими як R, Minitab, Excel, є
\[\nu = \frac {\left( \frac {s_A^2} {n_A} + \frac {s_B^2} {n_B} \right)^2} {\frac {\left( \frac {s_A^2} {n_A} \right)^2} {n_A - 1} + \frac {\left( \frac {s_B^2} {n_B} \right)^2} {n_B - 1}} = \frac {\left( \frac {s_A^2} {n_A} + \frac {s_B^2} {n_B} \right)^2} {\frac {s_A^4} {n_A^2(n_A - 1)} + \frac {s_B^4} {n_B^2(n_B - 1)}} \nonumber \]
Для типових задач в аналітичній хімії обчислені ступені свободи досить нечутливі до вибору рівняння.
Незалежно від того, як ми обчислюємо t exp, ми відкидаємо нульову гіпотезу, якщо t exp більше,\(t(\alpha, \nu)\) і зберігаємо нульову гіпотезу, якщо t exp менше або дорівнює\(t(\alpha, \nu)\).
Приклад\(\PageIndex{3}\) дає результати двох експериментів для визначення маси циркулюючої американської пенні. Визначте, чи є різниця в засобах цих аналізів на\(\alpha = 0.05\).
Рішення
Спочатку ми використовуємо F -тест, щоб визначити, чи можемо ми об'єднати відхилення. Ми завершили цей аналіз на прикладі\(\PageIndex{5}\), не знайшовши доказів істотної різниці, а це означає, що ми можемо об'єднати стандартні відхилення, отримавши
\[s_\text{pool} = \sqrt{\frac {(7 - 1)(0.051)^2 + (5 - 1)(0.037)^2} {7 + 5 - 2}} = 0.0459 \nonumber \]
з 10 ступенями свободи. Для порівняння засобів використовуємо наступну нульову гіпотезу і альтернативні гіпотези:
\[H_0 \text{: } \mu_A = \mu_B \quad \quad \quad H_A \text{: } \mu_A \neq \mu_B \nonumber \]
Оскільки ми використовуємо об'єднане стандартне відхилення, ми обчислюємо t exp як
\[t_\text{exp} = \frac {|3.117 - 3.081|} {0.0459} \times \sqrt{\frac {7 \times 5} {7 + 5}} = 1.34 \nonumber \]
Критичне значення для t (0,05, 10), з додатка 3, дорівнює 2,23. Оскільки t exp менше t (0,05, 10), ми зберігаємо нульову гіпотезу. Бо у\(\alpha = 0.05\) нас немає доказів того, що два набори копійок істотно відрізняються.
Одним із методів визначення %w/w Na 2 CO 3 в кальцинованій соді є використання кислотно-основного титрування. Коли два аналітики аналізують один і той же зразок кальцинованої соди, вони отримують результати, показані тут.
Аналітик А:\(86.82 \% \quad 87.04 \% \quad 86.93 \% \quad 87.01 \% \quad 86.20 \% \quad 87.00 \%\)
Аналітик B:\(81.01 \% \quad 86.15 \% \quad 81.73 \% \quad 83.19 \% \quad 80.27 \% \quad 83.93 \% \quad\)
Визначте, чи значна різниця в середніх значеннях при\(\alpha = 0.05\).
Рішення
Ми починаємо з звітності про середнє і стандартне відхилення для кожного аналітика.
\[\overline{X}_A = 86.83\% \quad \quad s_A = 0.32\% \nonumber \]
\[\overline{X}_B = 82.71\% \quad \quad s_B = 2.16\% \nonumber \]
Щоб визначити, чи можемо ми використовувати об'єднане стандартне відхилення, ми спочатку завершуємо F-тест, використовуючи наступні нульові та альтернативні гіпотези.
\[H_0 \text{: } s_A^2 = s_B^2 \quad \quad \quad H_A \text{: } s_A^2 \neq s_B^2 \nonumber \]
Розрахувавши F exp, отримаємо значення
\[F_\text{exp} = \frac {(2.16)^2} {(0.32)^2} = 45.6 \nonumber \]
Оскільки F exp більше критичного значення 7.15 для F (0,05, 5, 5) з Додатка 4, ми відкидаємо нульову гіпотезу і приймаємо альтернативну гіпотезу про те, що існує значна різниця між дисперсіями; таким чином, ми не можемо обчислити об'єднаний стандарт відхилення.
Для порівняння засобів для двох аналітиків ми використовуємо наступні нульові та альтернативні гіпотези.
\[H_0 \text{: } \overline{X}_A = \overline{X}_B \quad \quad \quad H_A \text{: } \overline{X}_A \neq \overline{X}_B \nonumber \]
Оскільки ми не можемо об'єднати стандартні відхилення, ми обчислюємо t exp як
\[t_\text{exp} = \frac {|86.83 - 82.71|} {\sqrt{\frac {(0.32)^2} {6} + \frac {(2.16)^2} {6}}} = 4.62 \nonumber \]
і обчислити ступені свободи як
\[\nu = \frac {\left( \frac {(0.32)^2} {6} + \frac {(2.16)^2} {6} \right)^2} {\frac {\left( \frac {(0.32)^2} {6} \right)^2} {6 + 1} + \frac {\left( \frac {(2.16)^2} {6} \right)^2} {6 + 1}} - 2 = 5.3 \approx 5 \nonumber \]
З додатка 3 критичне значення для t (0,05, 5) дорівнює 2,57. Оскільки t exp більше, ніж t (0,05, 5), ми відкидаємо нульову гіпотезу і приймаємо альтернативну гіпотезу про те, що засоби для двох аналітиків значно відрізняються\(\alpha = 0.05\).
Парні дані
Припустимо, ми оцінюємо новий метод контролю концентрації глюкози в крові у пацієнтів. Важливою частиною оцінки нового методу є порівняння його з усталеним методом. Який найкращий спосіб зібрати дані для цього дослідження? Оскільки різниця в рівні глюкози в крові серед пацієнтів велика, ми можемо не виявити невелику, але істотну різницю між методами, якщо ми використовуємо різних пацієнтів для збору даних для кожного методу. Використання парних даних, в яких ми аналізуємо кров кожного пацієнта за допомогою обох методів, запобігає значній дисперсії всередині популяції від негативного впливу на t -тест засобів.
Типові рівні глюкози в крові для більшості людей, які не мають діабету, коливається між 80-120 мг/дл (4.4—6.7 мМ), підвищуючись до 140 мг/дл (7,8 мМ) незабаром після їжі. Більш високі рівні є загальними для осіб, які є попередньо діабетичної або діабетичної.
Коли ми використовуємо парні дані, ми спочатку обчислюємо індивідуальні відмінності, d i, між парними реакціями кожного зразка. Використовуючи ці індивідуальні відмінності, ми потім обчислюємо середню різницю\(\overline{d}\), і стандартне відхилення відмінностей, s d. Нульова гіпотеза полягає в тому\(H_0 \text{: } d = 0\), що немає різниці між двома зразками та альтернативною гіпотезою полягає в тому\(H_A \text{: } d \neq 0\), що різниця між двома зразками є значною.
Тестова статистика, t exp, походить від довірчого інтервалу навколо\(\overline{d}\)
\[t_\text{exp} = \frac {|\overline{d}| \sqrt{n}} {s_d} \nonumber \]
де n - кількість парних зразків. Як і для інших форм t -тесту, ми порівнюємо t exp до\(t(\alpha, \nu)\), де ступені свободи\(\nu\), є n — 1. Якщо t exp більше\(t(\alpha, \nu)\), то відкидаємо нульову гіпотезу і приймаємо альтернативну гіпотезу. Ми зберігаємо нульову гіпотезу, якщо t exp менше або дорівнює t (a, o). Це відоме як парний t-тест.
Marecek et. al. розробили новий електрохімічний метод швидкого визначення концентрації антибіотика моненсін у чанах бродіння [Marecek, V.; Janchenova, H.; Brezina, M; Betti, M. Чим. Акт 1991, 244, 15—19]. Стандартним методом аналізу є тест на мікробіологічну активність, який є одночасно складним для завершення і трудомістким. Зразки збирали з ферментаційних чанів в різний час під час виробництва і аналізували на концентрацію моненсіна обома методами. Результати, у частках на тисячу (ppt), наведені в наступній таблиці.
| Зразок | Мікробіологічні | електрохімічний |
|---|---|---|
| 1 | 129.5 | 132.3 |
| 2 | 89.6 | 91.0 |
| 3 | 76.6 | 73.6 |
| 4 | 52.2 | 58.2 |
| 5 | 110.8 | 104.2 |
| 6 | 50.4 | 49.9 |
| 7 | 72.4 | 82.1 |
| 8 | 141.4 | 154.1 |
| 9 | 75.0 | 73.4 |
| 10 | 34.1 | 38.1 |
| 11 | 60.3 | 60.1 |
Чи є суттєва різниця між методами при\(\alpha = 0.05\)?
Рішення
Придбання зразків протягом тривалого періоду часу вводить значну залежну від часу зміну концентрації монензину. Оскільки варіація концентрації між зразками настільки велика, ми використовуємо парний t -тест з наступними нульовими та альтернативними гіпотезами.
\[H_0 \text{: } \overline{d} = 0 \quad \quad \quad H_A \text{: } \overline{d} \neq 0 \nonumber \]
Визначення різниці між методами як
\[d_i = (X_\text{elect})_i - (X_\text{micro})_i \nonumber \]
обчислюємо різницю для кожного зразка.
| зразок | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| \(d_i\) | 2.8 | 1.4 | —3.0 | 6.0 | —6.6 | —0,5 | 9.7 | 12,7 | —1.6 | 4.0 | —0.2 |
Середнє і стандартне відхилення для відмінностей складають відповідно 2,25 ppt і 5.63 ppt. Значення t exp дорівнює
\[t_\text{exp} = \frac {|2.25| \sqrt{11}} {5.63} = 1.33 \nonumber \]
що менше критичного значення 2,23 для t (0,05, 10) з додатка 3. Ми зберігаємо нульову гіпотезу і не знаходимо доказів істотної різниці в методах на\(\alpha = 0.05\).
Однією з важливих вимог до парного t -тесту є те, що детермінантні та невизначені помилки, які впливають на аналіз, повинні бути незалежними від концентрації аналіта. Якщо це не так, то проба з незвично високою концентрацією аналіту матиме незвично великий d i. Включення цієї вибірки в розрахунок\(\overline{d}\) і s d дає упереджену оцінку для очікуваного середнього і стандартного відхилення. Це рідко є проблемою для зразків, які охоплюють обмежений діапазон концентрацій аналітів, таких як у прикладі\(\PageIndex{6}\) або вправи\(\PageIndex{8}\). Коли парні дані охоплюють широкий діапазон концентрацій, однак, величина детермінантних і невизначений джерел похибки не може бути незалежною від концентрації аналіта; коли це правда, парний t -тест може дати оманливі результати, оскільки парні дані з найбільшим абсолютним домінують визначальні та невизначені помилки\(\overline{d}\). У цій ситуації регресійний аналіз, який є предметом наступної глави, є більш підходящим методом порівняння даних.
Важливість розрізнення парних і непарних даних варто вивчити уважніше. Нижче наведені дані з деякої роботи, яку я завершив з колегою, в якій ми розглядали концентрацію Zn в озері Ері на інтерфейсі повітря-вода та інтерфейс осадок-вода.
| зразок сайту | ppm Zn і інтерфейс повітря-вода | ppm Zn на межі межі осадо-вода |
| 1 | 0,430 | 0,415 |
| 2 | 0,266 | 0,238 |
| 3 | 0,457 | 0,390 |
| 4 | 0.531 | 0,410 |
| 5 | 0,707 | 0.605 |
| 6 | 0,716 | 0,609 |
Середнє значення і стандартне відхилення для ppm Zn на межі розділу повітря-вода становлять 0,5178 ppm і 0,01732 ppm, а середнє і стандартне відхилення для ppm Zn на межі осадок-вода складають 0,4445 ppm і 0,1418 ppm. Ми можемо використовувати ці значення, щоб намалювати нормальні розподіли як для відпускаючи середні та стандартні відхилення для вибірки, так\(\overline{X}\) і\(s\), служити оцінками для засобів і стандартних відхилень для популяції,\(\mu\) і\(\sigma\). Як ми бачимо на наступному малюнку
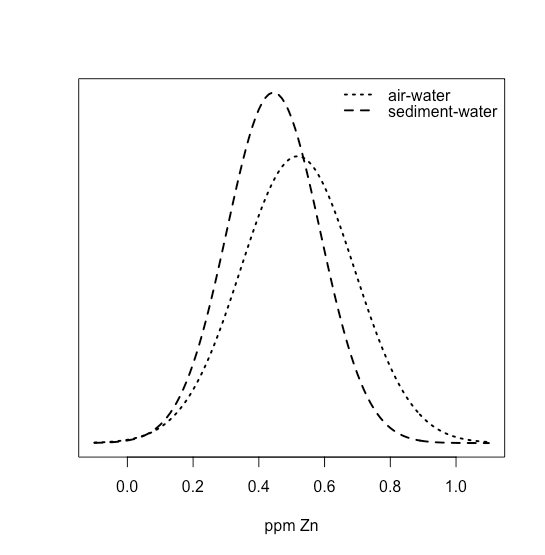
два розподіли сильно перекриваються, припускаючи, що t -тест їх засобів навряд чи знайде докази різниці. І все ж, ми також бачимо, що для кожної ділянки концентрація Zn на межі осаду - вода менше, ніж на межі розділу повітря-вода. При цьому різниця між концентрацією Zn на окремих ділянках досить велика, що маскує нашу здатність бачити різницю між двома інтерфейсами.
Якщо взяти відмінності між інтерфейсами «повітря-вода» і «осад - вода», то маємо значення 0,015, 0,028, 0,067, 0,121, 0,102 і 0,107 проміле Zn, із середнім значенням 0,07333 ppm Zn і стандартним відхиленням 0,04410 ppm Zn. Накладення всіх трьох нормальних розподілів
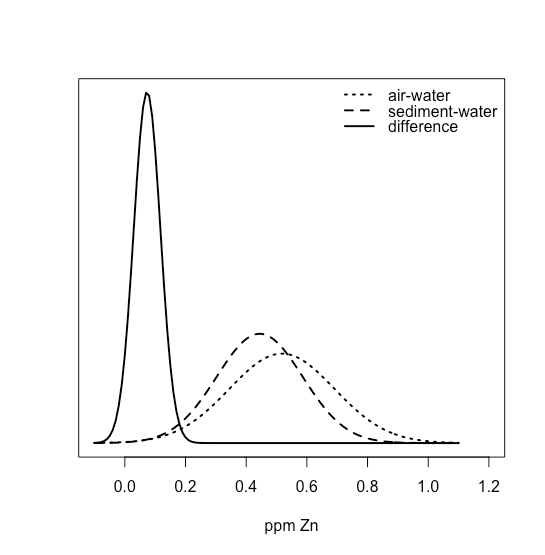
показує чітко, що більша частина нормального розподілу відмінностей лежить вище нуля, припускаючи, що t -тест може показати докази того, що різниця є значною.
Виділення
Таблиця\(\PageIndex{11}\) містить ще один набір даних, що дає маси за вибірку копійок. Ви помічаєте щось незвичайне в цих даних? З 100 копійок, включених в нашу більш ранню таблицю, жоден пенні не має маси менше 3 м У цій таблиці, однак маса однієї копійки менше 3 м Ми могли б запитати, чи настільки ця копійка відрізняється від інших копійок, що вона помилкова.
| 3.067 | 2.514 | 3.094 |
| 3.049 | 3.048 | 3.109 |
| 3.039 | 3.079 | 3.102 |
Вимірювання, яке не відповідає іншим вимірам, називається викидом. Викид може існувати з багатьох причин: викид може належати іншій популяції
Це канадська копійка?
або викид може бути забрудненим або іншим чином зміненим зразком
Копійка пошкоджена або незвично брудна?
або викид може бути наслідком помилки в аналізі
Ми забули тарувати залишок?
Незалежно від його джерела, наявність викидів компрометує будь-який змістовний аналіз наших даних. Є багато значущих тестів, які ми можемо використовувати для виявлення потенційних викидів, три з яких ми представляємо тут.
Q -Тест Діксона
Одним з найпоширеніших тестів значущості для виявлення викидів є Q-тест Діксона. Нульова гіпотеза полягає в тому, що немає викидів, а альтернативна гіпотеза полягає в тому, що існує викид. Q -тест порівнює розрив між підозрюваним викидом і його найближчим числовим сусідом з діапазоном всього набору даних (рис.\(\PageIndex{25}\)).
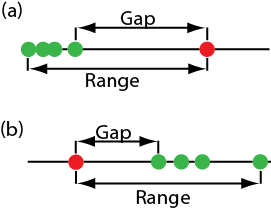
Статистика тесту, Q exp, становить
\[Q_\text{exp} = \frac {\text{gap}} {\text{range}} = \frac {|\text{outlier's value} - \text{nearest value}|} {\text{largest value} - \text{smallest value}} \nonumber \]
Це рівняння підходить для оцінки одного викиду. Інші форми Q -тесту Діксона дозволяють його розширення для виявлення декількох викидів [Rorabacher, D.B. анал. Хім. 1991, 63, 139—146].
Значення Q exp порівнюється з критичним значенням\(Q(\alpha, n)\), де\(\alpha\) є ймовірність того, що ми відхилимо допустиму точку даних (помилка типу 1) і n - загальна кількість точок даних. Щоб захистити від відхилення дійсної точки даних, зазвичай ми застосовуємо більш консервативний двоххвостий Q-тест, хоча можливий викид є найменшим або найбільшим значенням у наборі даних. Якщо Q exp більше\(Q(\alpha, n)\), то ми відхиляємо нульову гіпотезу і можемо виключити викиди. Ми зберігаємо можливий викид, коли Q exp менше або дорівнює\(Q(\alpha, n)\). Таблиця\(\PageIndex{12}\) містить значення\(Q(\alpha, n)\) для набору даних, який має 3—10 значень. Більш велика таблиця знаходиться в Додатку 5. Значення для\(Q(\alpha, n)\) припускають базовий нормальний розподіл.
| п | Q (0,05, н) |
|---|---|
| 3 | 0,970 |
| 4 | 0,829 |
| 5 | 0,710 |
| 6 | 0,625 |
| 7 | 0.568 |
| 8 | 0.526 |
| 9 | 0,493 |
| 10 | 0,466 |
Тест Грубба
Хоча Q -тест Діксона є загальним методом оцінки викидів, він більше не підтримується Міжнародною організацією зі стандартизації (ISO), яка рекомендує тест Грубба. Існує кілька версій тесту Грубба в залежності від кількості потенційних викидів. Тут ми розглянемо випадок, коли є єдиний підозрюваний викид.
Детальніше про цю рекомендацію див. Міжнародні стандарти ISO Guide 5752-2 «Точність (правдивість і точність) методів вимірювання та результатів - частина 2: основні методи визначення повторюваності та відтворюваності стандартного методу вимірювання» 1994.
Статистика тесту для тесту Грубба, G exp, - це відстань між середнім значенням зразка та потенційним викидом\(X_\text{out}\), з точки зору стандартного відхилення зразка, с.\(\overline{X}\)
\[G_\text{exp} = \frac {|X_\text{out} - \overline{X}|} {s} \nonumber \]
Порівнюємо значення G exp з критичним значенням\(G(\alpha, n)\), де\(\alpha\) є ймовірність того, що ми відхилимо дійсну точку даних, а n - кількість точок даних у вибірці. Якщо G exp більше\(G(\alpha, n)\), то ми можемо відхилити точку даних як викид, інакше ми збережемо точку даних як частину вибірки. Таблиця\(\PageIndex{13}\) містить значення G (0,05, n) для зразка, що містить 3—10 значень. Більш велика таблиця знаходиться в додатку 6. Значення для\(G(\alpha, n)\) припускають базовий нормальний розподіл.
| п | Г (0,05, н) |
|---|---|
| 3 | 1.15 |
| 4 | 1.481 |
| 5 | 1.715 |
| 6 | 1.887 |
| 7 | 2.020 |
| 8 | 2.126 |
| 9 | 2.215 |
| 10 | 2.290 |
Критерій Шовене
Наш остаточний метод виявлення викиду - критерій Шовене. На відміну від Q -Test Діксона та тесту Грубба, ви можете застосувати цей метод до будь-якого розподілу, якщо ви знаєте, як обчислити ймовірність для конкретного результату. Критерій Шовене стверджує, що ми можемо відхилити точку даних, якщо ймовірність отримання значення точки даних менше\((2n^{-1})\), де n - розмір вибірки. Наприклад, якщо n = 10, результат з ймовірністю менше\((2 \times 10)^{-1}\), або 0,05, вважається викидом.
Для обчислення ймовірності потенційного викиду спочатку обчислимо його стандартизоване відхилення, z
\[z = \frac {|X_\text{out} - \overline{X}|} {s} \nonumber \]
де\(X_\text{out}\) потенційний викид,\(\overline{X}\) - середнє значення зразка, а s - стандартне відхилення зразка. Зауважте, що це рівняння ідентично рівнянню для G exp у тесті Грубба. Для нормального розподілу можна знайти ймовірність отримання значення z за допомогою таблиці ймовірностей в Додатку 2.
Таблиця\(\PageIndex{11}\) містить маси за дев'ять циркулюючих США копійки. Один запис, 2,514 г, здається, є викидом. Визначте, чи є цей пенні викидом, використовуючи Q -тест, тест Грубба та критерій Шовене. Для Q -тесту і тесту Grubb, давайте\(\alpha = 0.05\).
Рішення
Для Q -тесту значення для\(Q_\text{exp}\) дорівнює
\[Q_\text{exp} = \frac {|2.514 - 3.039|} {3.109 - 2.514} = 0.882 \nonumber \]
З таблиці\(\PageIndex{12}\) критичне значення для Q (0,05, 9) дорівнює 0,493. Оскільки Q exp більше Q (0,05, 9), ми можемо припустити, що копійка з масою 2,514 г, ймовірно, є викидом.
Для тесту Грубба спочатку потрібні середнє значення і стандартне відхилення, які складають 3,011 г і 0,188 г відповідно. Значення для G exp дорівнює
\[G_\text{exp} = \frac {|2.514 - 3.011|} {0.188} = 2.64 \nonumber \]
Використовуючи Таблицю\(\PageIndex{13}\), знаходимо, що критичне значення для G (0,05, 9) дорівнює 2,215. Оскільки G exp більше G (0,05, 9), можна припустити, що копійка з масою 2,514 г, ймовірно, є викидом.
Для критерію Шовене критична ймовірність дорівнює\((2 \times 9)^{-1}\), або 0,0556. Значення z таке ж, як G exp, або 2,64. Використовуючи додаток 1, ймовірність для z = 2.64 дорівнює 0,00415. Оскільки ймовірність отримання маси 0,2514 г менше критичної ймовірності, можна припустити, що копійка з масою 2,514 г, швидше за все, є викидом.
Ви повинні проявляти обережність при використанні тесту на значущість для викидів, оскільки є ймовірність, що ви відхилите дійсний результат. Крім того, слід уникати відхилення викиду, якщо це призводить до точності, яка набагато краща, ніж очікувалося, на основі поширення невизначеності. Враховуючи ці побоювання, не дивно, що деякі статистики застерігають проти видалення викидів [Демінг, У.Е. Статистичний аналіз даних; Wiley: Нью-Йорк, 1943 (перевидано Dover: Нью-Йорк, 1961); стор. 171].
Ви також можете прийняти більш сувору вимогу щодо відхилення даних. Наприклад, при використанні тесту Грубба, настанови ISO 5752 пропонують зберегти значення, якщо ймовірність відхилення його більше\(\alpha = 0.05\), ніж, і позначити значення як «відсторонювач», якщо ймовірність відхилення від нього знаходиться між\(\alpha = 0.05\) і\(\alpha = 0.01\). «Відхилення» зберігається, якщо немає вагомих причин для його відхилення. Керівні принципи рекомендують використовувати\(\alpha = 0.01\) як мінімальний критерій для відхилення можливого викиду.
З іншого боку, тестування на викиди може надати корисну інформацію, якщо ми спробуємо зрозуміти джерело підозрюваного викиду. Наприклад, викид в таблиці\(\PageIndex{11}\) являє собою значну зміну маси копійки (приблизно на 17% зменшення маси), що є результатом зміни складу американського пенні. У 1982 році склад американського пенні змінився з латунного сплаву, який становив 95% w/w Cu і 5% w/w Zn (з номінальною масою 3,1 г), до чистого цинкового сердечника, покритого міддю (номінальною масою 2,5 г) [Richardson, T.H. J. Chem. Едук. 1991, 68, 310—311]. Копійки в таблиці\(\PageIndex{11}\), таким чином, були залучені з різних популяцій.
Калібрування даних
Калібрувальна крива є одним з найважливіших інструментів аналітичної хімії, оскільки вона дозволяє нам визначити концентрацію аналіту у зразку шляхом вимірювання сигналу, який він генерує при розміщенні в приладі, наприклад спектрофотометрі. Щоб визначити концентрацію аналіта, ми повинні знати взаємозв'язок між сигналом, який ми вимірюємо\(S\), та концентрацією аналіта\(C_A\), яку ми можемо записати як
\[S = k_A C_A + S_{blank} \nonumber \]
де\(k_A\) - чутливість калібрувальної кривої і\(S_{blank}\) сигнал при відсутності аналіту.
Як ми знаходимо найкращу оцінку для цього співвідношення між сигналом та концентрацією аналіту? Коли калібрувальна крива є прямолінійною, ми представляємо її за допомогою наступної математичної моделі
\[y = \beta_0 + \beta_1 x \nonumber \]
де y - виміряний сигнал аналіта, S, а x - відома концентрація аналіта в серії стандартних розчинів.\(C_A\) Константи\(\beta_0\) і\(\beta_1\) є, відповідно, очікуваним y -перехопленням калібрувальної кривої та очікуваним нахилом. Через невизначеність наших вимірювань найкраще, що ми можемо зробити, це оцінити значення для\(\beta_0\) і\(\beta_1\), які ми представляємо як b 0 і b 1. Метою лінійного регресійного аналізу є визначення найкращих оцінок для b 0 та b 1.
Незважена лінійна регресія з помилками у y
Найбільш поширений метод завершення лінійної регресії робить три припущення:
- різниця між нашими експериментальними даними та обчисленою лінією регресії є результатом невизначеної помилки, що впливають на y
- будь-які невизначені помилки, які впливають на y, зазвичай розподіляються
- що невизначені помилки в y не залежать від значення x
Оскільки ми припускаємо, що невизначені помилки однакові для всіх стандартів, кожен стандарт однаково вносить свій внесок у нашу оцінку нахилу та y -перехоплення. З цієї причини результат вважається незваженою лінійною регресією.
Друге припущення, як правило, вірно через центральну граничну теорему, яку ми розглядали раніше. Обґрунтованість двох інших припущень менш очевидна, і ви повинні оцінити їх, перш ніж приймати результати лінійної регресії. Зокрема, перше припущення завжди підозрюється, оскільки, безумовно, є певна невизначена похибка вимірювання x. Коли ми готуємо калібрувальну криву, однак, незвично виявити, що невизначеність у сигналі, S, значно більша, ніж невизначеність концентрації аналіта\(C_A\). За таких обставин перше припущення зазвичай є розумним.
Як працює лінійна регресія
Щоб зрозуміти логіку лінійної регресії, розглянемо приклад на малюнку\(\PageIndex{26}\), який показує три точки даних і дві можливі прямі лінії, які можуть обґрунтовано пояснити дані. Як ми вирішуємо, наскільки добре ці прямі лінії підходять до даних, і як ми можемо визначити, яка, якщо так, є найкращою прямою лінією?
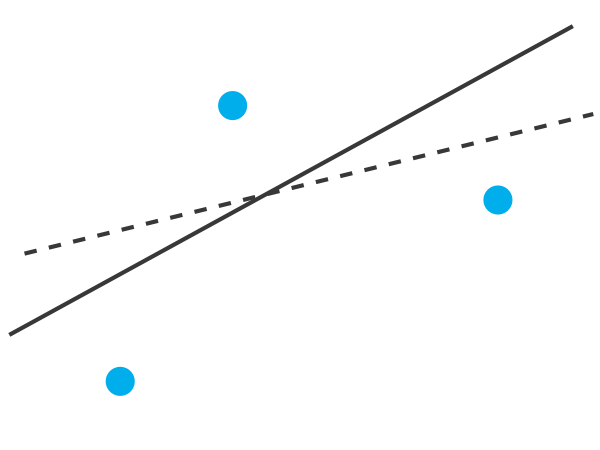
Давайте зосередимося на суцільній лінії на малюнку\(\PageIndex{26}\). Рівняння для цього рядка
\[\hat{y} = b_0 + b_1 x \nonumber \]
де b 0 і b 1 - оцінки для y -перехоплення та нахилу, і\(\hat{y}\) є прогнозованим значенням y для будь-якого значення x. Оскільки ми припускаємо, що вся невизначеність є результатом невизначеної помилки у, різниця між y і\(\hat{y}\) для кожного значення x є залишковою похибкою, r, в нашій математичній моделі.
\[r_i = (y_i - \hat{y}_i) \nonumber \]
\(\PageIndex{27}\)На малюнку показані залишкові помилки для трьох точок даних. Чим менше загальна залишкова помилка, R, яку ми визначаємо як
\[R = \sum_{i = 1}^{n} (y_i - \hat{y}_i)^2 \nonumber \]
тим краще прилягання між прямою лінією і даними. У лінійному регресійному аналізі ми шукаємо значення b 0 та b 1, які дають найменшу загальну залишкову похибку.
Причина квадратизації окремих залишкових помилок полягає в тому, щоб запобігти позитивній залишковій помилку від скасування негативної залишкової помилки. Ви бачили це раніше в рівняннях для вибірки і популяції стандартних відхилень, введені в главі 4. З цього рівняння також видно, чому лінійну регресію іноді називають методом найменших квадратів.
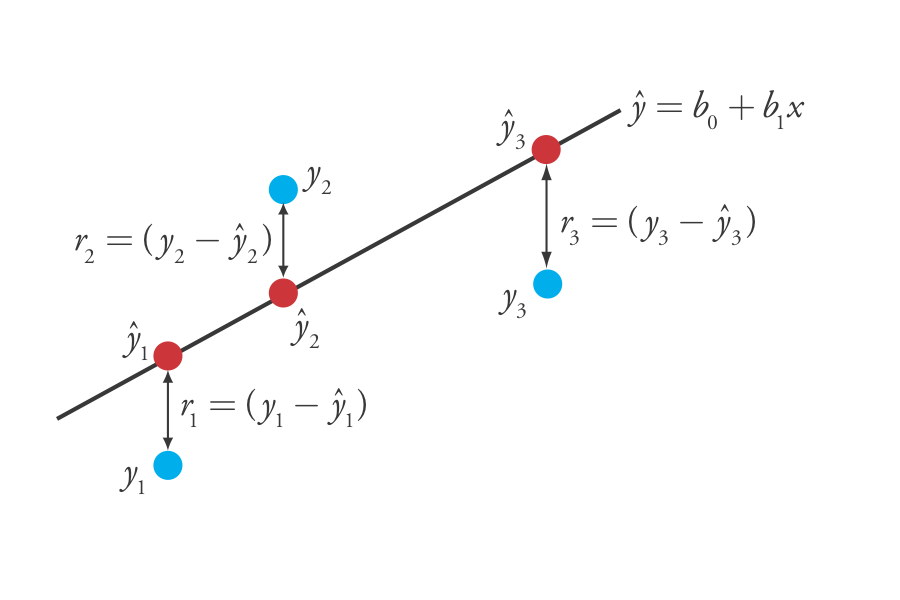
Пошук нахилу та y -перехоплення для регресійної моделі
Хоча формально ми не будемо розробляти математичні рівняння для лінійного регресійного аналізу, ви можете знайти похідні в багатьох стандартних статистичних текстах [Див., наприклад, Draper, Н.Р.; Smith, H. прикладний регресійний аналіз, 3-е видання; Wiley: Нью-Йорк, 1998]. Отримане рівняння для ухилу, b 1, дорівнює
\[b_1 = \frac {n \sum_{i = 1}^{n} x_i y_i - \sum_{i = 1}^{n} x_i \sum_{i = 1}^{n} y_i} {n \sum_{i = 1}^{n} x_i^2 - \left( \sum_{i = 1}^{n} x_i \right)^2} \nonumber \]
і рівняння для y -перехоплення, b 0, дорівнює
\[b_0 = \frac {\sum_{i = 1}^{n} y_i - b_1 \sum_{i = 1}^{n} x_i} {n} \nonumber \]
Хоча ці рівняння здаються грізними, необхідно лише оцінити наступні чотири підсумовування
\[\sum_{i = 1}^{n} x_i \quad \sum_{i = 1}^{n} y_i \quad \sum_{i = 1}^{n} x_i y_i \quad \sum_{i = 1}^{n} x_i^2 \nonumber \]
Багато калькуляторів, електронних таблиць та інших статистичних програмних пакетів здатні виконувати лінійний регресійний аналіз на основі цієї моделі; докладніше про завершення лінійного регресійного аналізу за допомогою R. наступний приклад.
Використовуючи дані калібрування в наступній таблиці, визначте взаємозв'язок між сигналом та концентрацією аналіта\(x_i\), використовуючи незважену лінійну регресію.\(y_i\)
Рішення
Ми починаємо з налаштування таблиці, яка допоможе нам організувати розрахунок.
| \(x_i\) | \(y_i\) | \(x_i y_i\) | \(x_i^2\) |
|---|---|---|---|
| \ (x_i\) ">0.000 | \ (y_i\) ">0.00 | \ (x_i y_i\) ">0.000 | \ (x_i ^ 2\) ">0.000 |
| \ (x_i\) ">0.100 | \ (y_i\) ">12,36 | \ (x_i\) ">1.236 | \ (x_i^2\) ">0,010 |
| \ (x_i\) ">0,200 | \ (y_i\) ">24.83 | \ (x_i\) ">4.966 | \ (x_i^2\) ">0.040 |
| \ (x_i\) ">0,300 | \ (y_i\) ">35.91 | \ (x_i\) ">10.773 | \ (x_i^2\) ">0,090 |
| \ (x_i\) ">0,400 | \ (y_i\) ">48.79 | \ (x_i\) ">19.516 | \ (x_i^2\) ">0.160 |
| \ (x_i\) ">0,500 | \ (y_i\) ">60.42 | \ (x_i\) ">30.210 | \ (x_i^2\) ">0,250 |
Додавання значень у кожному стовпці дає
\[\sum_{i = 1}^{n} x_i = 1.500 \quad \sum_{i = 1}^{n} y_i = 182.31 \quad \sum_{i = 1}^{n} x_i y_i = 66.701 \quad \sum_{i = 1}^{n} x_i^2 = 0.550 \nonumber \]
Підставляючи ці значення в рівняння для нахилу і y -перехоплення дає
\[b_1 = \frac {(6 \times 66.701) - (1.500 \times 182.31)} {(6 \times 0.550) - (1.500)^2} = 120.706 \approx 120.71 \nonumber \]
\[b_0 = \frac {182.31 - (120.706 \times 1.500)} {6} = 0.209 \approx 0.21 \nonumber \]
Взаємозв'язок між\(S\) сигналом та концентрацією аналіта\(C_A\), отже, становить
\[S = 120.71 \times C_A + 0.21 \nonumber \]
Наразі ми зберігаємо два знака після коми, щоб відповідати кількості десяткових знаків у сигналі. Отримана калібрувальна крива показана на малюнку\(\PageIndex{28}\).
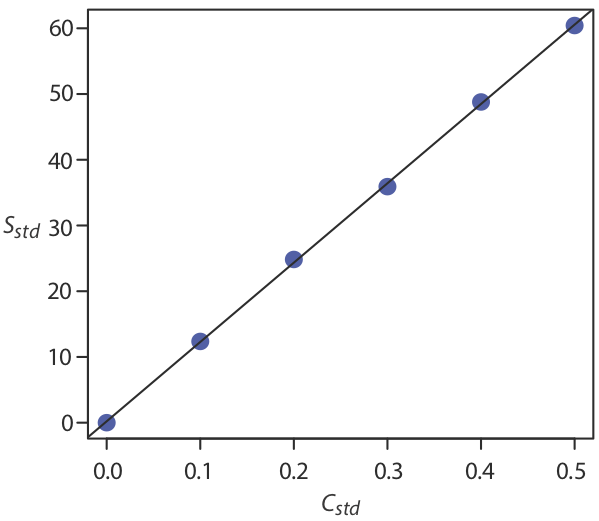
Невизначеність у регресійній моделі
Як ми бачимо на малюнку\(\PageIndex{28}\), через невизначені помилки в сигналі лінія регресії не проходить через точний центр кожної точки даних. Сукупне відхилення наших даних від лінії регресії - загальна залишкова похибка - пропорційно невизначеності в регресії. Ми називаємо цю невизначеність стандартним відхиленням про регресію, s r, яка дорівнює
\[s_r = \sqrt{\frac {\sum_{i = 1}^{n} \left( y_i - \hat{y}_i \right)^2} {n - 2}} \nonumber \]
де y i - i експериментальне значення, і\(\hat{y}_i\) відповідне значення, передбачене рівнянням регресії\(\hat{y} = b_0 + b_1 x\). Зауважте, що знаменник вказує на те, що наш регресійний аналіз має n - 2 ступеня свободи - ми втрачаємо два ступені свободи, оскільки використовуємо два параметри, нахил і y -перехоплення, для обчислення\(\hat{y}_i\).
Більш корисним поданням невизначеності в нашому регресійному аналізі є врахування впливу невизначених помилок на нахил, b 1, і y -перехоплення, b 0, який ми виражаємо як стандартні відхилення.
\[s_{b_1} = \sqrt{\frac {n s_r^2} {n \sum_{i = 1}^{n} x_i^2 - \left( \sum_{i = 1}^{n} x_i \right)^2}} = \sqrt{\frac {s_r^2} {\sum_{i = 1}^{n} \left( x_i - \overline{x} \right)^2}} \nonumber \]
\[s_{b_0} = \sqrt{\frac {s_r^2 \sum_{i = 1}^{n} x_i^2} {n \sum_{i = 1}^{n} x_i^2 - \left( \sum_{i = 1}^{n} x_i \right)^2}} = \sqrt{\frac {s_r^2 \sum_{i = 1}^{n} x_i^2} {n \sum_{i = 1}^{n} \left( x_i - \overline{x} \right)^2}} \nonumber \]
Ми використовуємо ці стандартні відхилення для встановлення довірчих інтервалів для очікуваного нахилу\(\beta_1\), і очікуваного y -перехоплення,\(\beta_0\)
\[\beta_1 = b_1 \pm t s_{b_1} \nonumber \]
\[\beta_0 = b_0 \pm t s_{b_0} \nonumber \]
де виділено t для рівня значущості,\(\alpha\) а для n — 2 ступенів свободи. Зауважте, що ці рівняння не містять коефіцієнта\((\sqrt{n})^{-1}\) видимого в довірчих інтервалах,\(\mu\) оскільки довірчий інтервал тут базується на одній лінії регресії.
Обчисліть 95% довірчих інтервалів для нахилу та y -перехоплення з Прикладу\(\PageIndex{10}\).
Рішення
Почнемо з розрахунку стандартного відхилення про регресію. Для цього ми повинні обчислити передбачені сигнали\(\hat{y}_i\), використовуючи нахил і y -перехоплення з Прикладу\(\PageIndex{10}\), і квадрати залишкової похибки,\((y_i - \hat{y}_i)^2\). Використовуючи останній стандарт як приклад, ми виявимо, що прогнозований сигнал
\[\hat{y}_6 = b_0 + b_1 x_6 = 0.209 + (120.706 \times 0.500) = 60.562 \nonumber \]
і що квадрат залишкової помилки
\[(y_i - \hat{y}_i)^2 = (60.42 - 60.562)^2 = 0.2016 \approx 0.202 \nonumber \]
Наступна таблиця відображає результати для всіх шести рішень.
| \(x_i\) | \(y_i\) | \(\hat{y}_i\) | \(\left( y_i - \hat{y}_i \right)^2\) |
|---|---|---|---|
| \ (x_i\) ">0.000 | \ (y_i\) ">0.00 | \ (\ hat {y} _i\) ">0.209 | \ (\ ліворуч (y_i -\ hat {y} _i\ праворуч) ^2\) ">0.0437 |
| \ (x_i\) ">0.100 | \ (y_i\) ">12,36 | \ (\ hat {y} _i\) ">12.280 | \ (\ ліворуч (y_i -\ hat {y} _i\ праворуч) ^2\) ">0.0064 |
| \ (x_i\) ">0,200 | \ (y_i\) ">24.83 | \ (\ hat {y} _i\) ">24.350 | \ (\ ліворуч (y_i -\ hat {y} _i\ праворуч) ^2\) ">0.2304 |
| \ (x_i\) ">0,300 | \ (y_i\) ">35.91 | \ (\ hat {y} _i\) ">36.421 | \ (\ ліворуч (y_i -\ hat {y} _i\ праворуч) ^2\) ">0.2611 |
| \ (x_i\) ">0,400 | \ (y_i\) ">48.79 | \ (\ hat {y} _i\) ">48.491 | \ (\ ліворуч (y_i -\ hat {y} _i\ праворуч) ^2\) ">0.0894 |
| \ (x_i\) ">0,500 | \ (y_i\) ">60.42 | \ (\ hat {y} _i\) ">60.562 | \ (\ ліворуч (y_i -\ hat {y} _i\ праворуч) ^2\) ">0.0202 |
Складання даних в останньому стовпці дає чисельник у рівнянні для стандартного відхилення про регресію; таким чином
\[s_r = \sqrt{\frac {0.6512} {6 - 2}} = 0.4035 \nonumber \]
Далі обчислюємо стандартні відхилення для ухилу і y -перехоплення. Значення термінів підсумовування взяті з Приклад\(\PageIndex{10}\).
\[s_{b_1} = \sqrt{\frac {6 \times (0.4035)^2} {(6 \times 0.550) - (1.500)^2}} = 0.965 \nonumber \]
\[s_{b_0} = \sqrt{\frac {(0.4035)^2 \times 0.550} {(6 \times 0.550) - (1.500)^2}} = 0.292 \nonumber \]
Нарешті, 95% довірчих інтервалів (\(\alpha = 0.05\), 4 ступеня свободи) для нахилу та y -перехоплення
\[\beta_1 = b_1 \pm ts_{b_1} = 120.706 \pm (2.78 \times 0.965) = 120.7 \pm 2.7 \nonumber \]
\[\beta_0 = b_0 \pm ts_{b_0} = 0.209 \pm (2.78 \times 0.292) = 0.2 \pm 0.80 \nonumber \]
де t (0,05, 4) з додатка 3 дорівнює 2.78. Стандартне відхилення щодо регресії, s r, говорить про те, що сигнал, S std, точний до одного знака після коми. З цієї причини ми повідомляємо нахил і y -перехоплення до одного знака після коми.
Використання моделі регресії для визначення значення для x, заданого значення для y
Після того, як ми отримаємо наше рівняння регресії, легко визначити концентрацію аналіту в зразку. Наприклад, коли ми використовуємо нормальну калібрувальну криву, ми вимірюємо сигнал для нашого зразка, S samp, і обчислюємо концентрацію аналіта, C A, використовуючи рівняння регресії.
\[C_A = \frac {S_{samp} - b_0} {b_1} \nonumber \]
Менш очевидним є те, як повідомити про довірчий інтервал для C A, який виражає невизначеність в нашому аналізі. Для обчислення довірчого інтервалу нам потрібно знати стандартне відхилення в концентрації аналіта\(s_{C_A}\), яке задається наступним рівнянням
\[s_{C_A} = \frac {s_r} {b_1} \sqrt{\frac {1} {m} + \frac {1} {n} + \frac {\left( \overline{S}_{samp} - \overline{S}_{std} \right)^2} {(b_1)^2 \sum_{i = 1}^{n} \left( C_{std_i} - \overline{C}_{std} \right)^2}} \nonumber \]
де m - кількість реплікацій, які ми використовуємо для встановлення середнього сигналу зразка, S samp, n - кількість калібрувальних стандартів, S std - середній сигнал для калібрування стандарти,\(C_{std_i}\) і\(\overline{C}_{std}\) є індивідуальними та середніми концентраціями для стандартів калібрування. Знаючи значення\(s_{C_A}\), довірчий інтервал для концентрації аналіта становить
\[\mu_{C_A} = C_A \pm t s_{C_A} \nonumber \]
де\(\mu_{C_A}\) - очікуване значення С А при відсутності детермінантних похибок, а при значенні t базується на бажаному рівні довіри і n — 2 ступеня свободи.
Ретельне вивчення цих рівнянь повинно переконати вас, що ми можемо зменшити невизначеність прогнозованої концентрації аналіту,\(C_A\) якщо ми збільшимо кількість стандартів\(n\), збільшимо кількість повторюваних зразків, які ми аналізуємо\(m\), і якщо середній сигнал зразка, \(\overline{S}_{samp}\), дорівнює середньому сигналу за стандартами,\(\overline{S}_{std}\). Коли це практично, слід спланувати калібрувальну криву так, щоб S samp потрапляла посередині калібрувальної кривої. Для отримання додаткової інформації про ці рівняння регресії див. (а) Міллер, Дж. Аналітик 1991, 116, 3—14; (б) Шараф, М.А.; Іллман, Д.; Ковальський, Б.Р. Хемометрія, Wiley-Interscience: Нью-Йорк, 1986, стор. 126-127; (c) Комітет з аналітичних методів» Невизначеність концентрацій, оцінених в результаті калібрувальних експериментів», Технічний бриф КУА, березень 2006.
Рівняння стандартного відхилення в концентрації аналіта записано в терміні калібрувального експерименту. Тут наведено більш загальну форму рівняння, записаного через x і y.
\[s_{x} = \frac {s_r} {b_1} \sqrt{\frac {1} {m} + \frac {1} {n} + \frac {\left( \overline{Y} - \overline{y} \right)^2} {(b_1)^2 \sum_{i = 1}^{n} \left( x_i - \overline{x} \right)^2}} \nonumber \]
Три репліковані аналізи для зразка, який містить невідому концентрацію аналіту, дає значення для S samp 29,32, 29.16 та 29.51 (довільні одиниці). Використовуючи результати з\(\PageIndex{10}\) Example and Example\(\PageIndex{11}\), визначити концентрацію аналіта, C A та його 95% довірчий інтервал.
Рішення
Середній сигнал становить 29.33, який, використовуючи нахил і y -перехоплення з Прикладу\(\PageIndex{10}\), дає концентрацію аналіта як\(\overline{S}_{samp}\)
\[C_A = \frac {\overline{S}_{samp} - b_0} {b_1} = \frac {29.33 - 0.209} {120.706} = 0.241 \nonumber \]
Щоб розрахувати стандартне відхилення для концентрації аналіта, ми повинні визначити значення для\(\overline{S}_{std}\) і за\(\sum_{i = 1}^{2} (C_{std_i} - \overline{C}_{std})^2\). Перший - це якраз середній сигнал по нормам калібрування, який, використовуючи дані в таблиці\(\PageIndex{10}\), дорівнює 30.385. Обчислення\(\sum_{i = 1}^{2} (C_{std_i} - \overline{C}_{std})^2\) виглядає грізним, але ми можемо спростити його обчислення, визнавши, що ця сума квадратів є чисельником у рівнянні стандартного відхилення; таким чином,
\[\sum_{i = 1}^{n} (C_{std_i} - \overline{C}_{std})^2 = (s_{C_{std}})^2 \times (n - 1) \nonumber \]
де\(s_{C_{std}}\) - стандартне відхилення для концентрації аналіту в нормах калібрування. Використовуючи дані в таблиці,\(\PageIndex{10}\) ми знаходимо, що\(s_{C_{std}}\) це 0.1871 і
\[\sum_{i = 1}^{n} (C_{std_i} - \overline{C}_{std})^2 = (0.1872)^2 \times (6 - 1) = 0.175 \nonumber \]
Підставляємо відомі значення в рівняння для\(s_{C_A}\) дач
\[s_{C_A} = \frac {0.4035} {120.706} \sqrt{\frac {1} {3} + \frac {1} {6} + \frac {(29.33 - 30.385)^2} {(120.706)^2 \times 0.175}} = 0.0024 \nonumber \]
Нарешті, 95% довірчий інтервал для 4 ступенів свободи
\[\mu_{C_A} = C_A \pm ts_{C_A} = 0.241 \pm (2.78 \times 0.0024) = 0.241 \pm 0.007 \nonumber \]
\(\PageIndex{29}\)На малюнку показана калібрувальна крива з кривими, що показують 95% довірчий інтервал для C A.
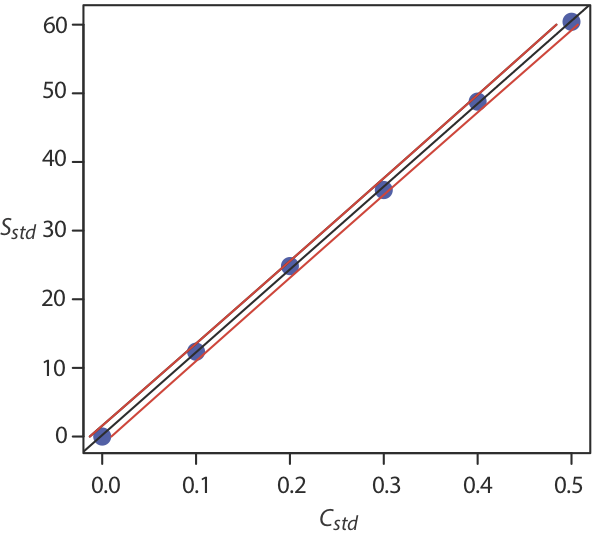
Оцінка регресійної моделі
Ніколи не слід приймати результат лінійного регресійного аналізу без оцінки достовірності моделі. Мабуть, найпростішим способом оцінки регресійного аналізу є вивчення залишкових помилок. Як ми бачили раніше, залишкова похибка для єдиного стандарту калібрування, r i, дорівнює
\[r_i = (y_i - \hat{y}_i) \nonumber \]
Якщо модель регресії дійсна, то залишкові помилки повинні розподілятися випадковим чином щодо середньої залишкової похибки нуля, без видимої тенденції до менших або більших залишкових помилок (рис.\(\PageIndex{30a}\)). Такі тенденції, як у малюнку\(\PageIndex{30b}\) та малюнку,\(\PageIndex{30c}\) свідчать про те, що принаймні одне з припущень моделі є неправильним. Наприклад, тенденція до більших залишкових помилок при більш високих концентраціях, Рисунок\(\PageIndex{30b}\), свідчить про те, що невизначені помилки, що впливають на сигнал, не залежать від концентрації аналіта. На малюнку\(\PageIndex{30c}\) залишкові помилки не є випадковими, що говорить про те, що ми не можемо моделювати дані за допомогою прямолінійного співвідношення. Регресійні методи для останніх двох випадків розглядаються в наступних розділах.
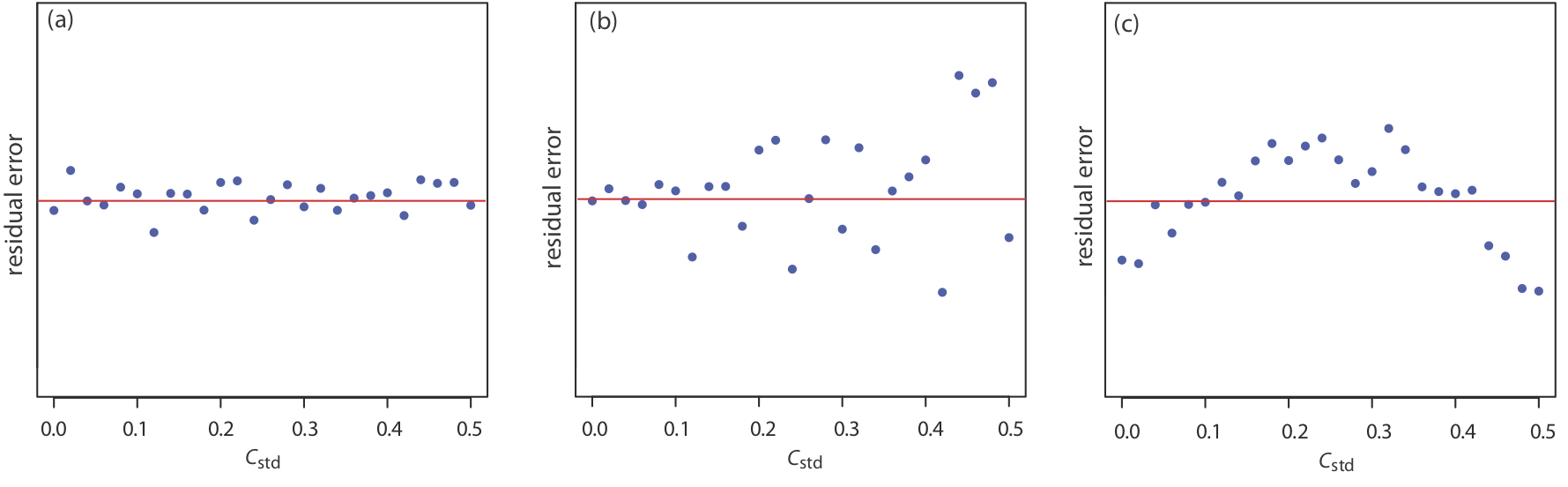
Використовуйте свої результати з вправи,\(\PageIndex{10}\) щоб побудувати залишковий сюжет і пояснити його значення.
Рішення
Для створення залишкової ділянки нам потрібно обчислити залишкову похибку для кожного стандарту. Наступна таблиця містить відповідну інформацію.
| \(x_i\) | \(y_i\) | \(\hat{y}_i\) | \(y_i - \hat{y}_i\) |
|---|---|---|---|
| \ (x_i\) ">0.000 | \ (y_i\) ">0.000 | \ (\ hat {y} _i\) ">0.0015 | \ (y_i -\ hat {y} _i\) ">—0.0015 |
| \ (x_i\) ">\(1.55 \times 10^{-3}\) | \ (y_i\) ">0,050 | \ (\ hat {y} _i\) ">0.0473 | \ (y_i -\ hat {y} _i\) ">0.0027 |
| \ (x_i\) ">\(3.16 \times 10^{-3}\) | \ (y_i\) ">0,093 | \ (\ hat {y} _i\) ">0.0949 | \ (y_i -\ hat {y} _i\) ">—0.0019 |
| \ (x_i\) ">\(4.74 \times 10^{-3}\) | \ (y_i\) ">0.143 | \ (\ hat {y} _i\) ">0.1417 | \ (y_i -\ hat {y} _i\) ">0.0013 |
| \ (x_i\) ">\(6.34 \times 10^{-3}\) | \ (y_i\) ">0.188 | \ (\ hat {y} _i\) ">0.1890 | \ (y_i -\ hat {y} _i\) ">—0,0010 |
| \ (x_i\) ">\(7.92 \times 10^{-3}\) | \ (y_i\) ">0,236 | \ (\ hat {y} _i\) ">0.2357 | \ (y_i -\ hat {y} _i\) ">0.0003 |
На малюнку нижче показана схема отриманих залишкових помилок. Залишкові помилки виявляються випадковими, хоча вони чергуються за знаком, і вони не виявляють значної залежності від концентрації аналіта. Разом ці спостереження свідчать про те, що наша регресійна модель є доречною.
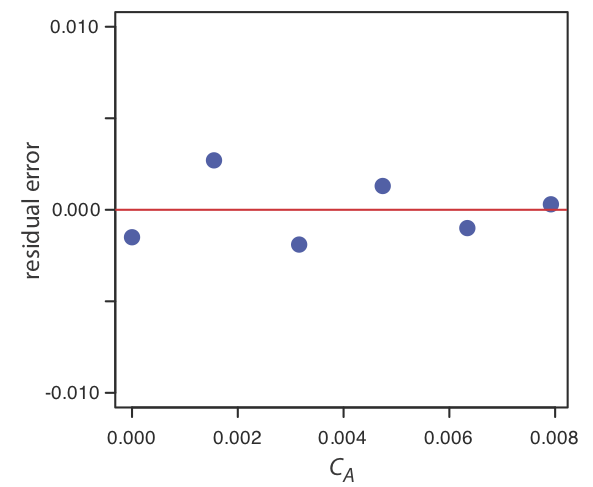
Зважена лінійна регресія з помилками у y
Наша обробка лінійної регресії до цього моменту передбачає, що будь-які невизначені помилки, які впливають на y, не залежать від значення x. Якщо це припущення помилкове, то ми повинні включити дисперсію для кожного значення y в наше визначення y -перехоплення, b 0, і нахилу, b 1; таким чином
\[b_0 = \frac {\sum_{i = 1}^{n} w_i y_i - b_1 \sum_{i = 1}^{n} w_i x_i} {n} \nonumber \]
\[b_1 = \frac {n \sum_{i = 1}^{n} w_i x_i y_i - \sum_{i = 1}^{n} w_i x_i \sum_{i = 1}^{n} w_i y_i} {n \sum_{i =1}^{n} w_i x_i^2 - \left( \sum_{i = 1}^{n} w_i x_i \right)^2} \nonumber \]
де w i - ваговий коефіцієнт, який враховує дисперсію в y i
\[w_i = \frac {n (s_{y_i})^{-2}} {\sum_{i = 1}^{n} (s_{y_i})^{-2}} \nonumber \]
і\(s_{y_i}\) є стандартним відхиленням для y i. У зваженій лінійній регресії внесок кожної xy -пари в лінію регресії обернено пропорційний точності y i; тобто чим точніше значення y, тим більший її внесок у регресію.
Тут наведені дані для зовнішньої стандартизації, в якій s std є стандартним відхиленням для трьох реплікаційних визначення сигналу.
| \(C_{std}\)(довільні одиниці) | \(S_{std}\)(довільні одиниці) | \(s_{std}\) |
|---|---|---|
| \ (C_ {std}\) (довільні одиниці виміру) ">0.000 | \ (S_ {std}\) (довільні одиниці виміру) ">0.00 | \ (s_ {std}\) ">0.02 |
| \ (C_ {std}\) (довільні одиниці виміру) ">0.100 | \ (S_ {std}\) (довільні одиниці виміру) ">12.36 | \ (s_ {std}\) ">0.02 |
| \ (C_ {std}\) (довільні одиниці виміру) ">0.200 | \ (S_ {std}\) (довільні одиниці виміру) ">24.83 | \ (s_ {std}\) ">0.07 |
| \ (C_ {std}\) (довільні одиниці виміру) ">0.300 | \ (S_ {std}\) (довільні одиниці виміру) ">35.91 | \ (s_ {std}\) ">0.13 |
| \ (C_ {std}\) (довільні одиниці виміру) ">0.400 | \ (S_ {std}\) (довільні одиниці виміру) ">48.79 | \ (s_ {std}\) ">0.22 |
| \ (C_ {std}\) (довільні одиниці виміру) ">0.500 | \ (S_ {std}\) (довільні одиниці виміру) ">60.42 | \ (s_ {std}\) ">0.33 |
Визначте рівняння калібрувальної кривої за допомогою зваженої лінійної регресії. Коли ви працюєте над цим прикладом, пам'ятайте, що x відповідає C std, а що y відповідає S std.
Рішення
Ми починаємо з налаштування таблиці, яка допоможе в обчисленні вагових коефіцієнтів.
| \(C_{std}\)(довільні одиниці) | \(S_{std}\)(довільні одиниці) | \(s_{std}\) | \((s_{y_i})^{-2}\) | \(w_i\) |
|---|---|---|---|---|
| \ (C_ {std}\) (довільні одиниці виміру) ">0.000 | \ (S_ {std}\) (довільні одиниці виміру) ">0.00 | \ (s_ {std}\) ">0.02 | \ (s_ {y_i}) ^ {-2}\) ">2500.00 | \ (w_i\) ">2.8339 |
| \ (C_ {std}\) (довільні одиниці виміру) ">0.100 | \ (S_ {std}\) (довільні одиниці виміру) ">12.36 | \ (s_ {std}\) ">0.02 | \ (s_ {y_i}) ^ {-2}\) ">250.00 | \ (w_i\) ">2.8339 |
| \ (C_ {std}\) (довільні одиниці виміру) ">0.200 | \ (S_ {std}\) (довільні одиниці виміру) ">24.83 | \ (s_ {std}\) ">0.07 | \ (s_ {y_i}) ^ {-2}\) ">204.08 | \ (w_i\) ">0.2313 |
| \ (C_ {std}\) (довільні одиниці виміру) ">0.300 | \ (S_ {std}\) (довільні одиниці виміру) ">35.91 | \ (s_ {std}\) ">0.13 | \ (s_ {y_i}) ^ {-2}\) ">59,17 | \ (w_i\) ">0.0671 |
| \ (C_ {std}\) (довільні одиниці виміру) ">0.400 | \ (S_ {std}\) (довільні одиниці виміру) ">48.79 | \ (s_ {std}\) ">0.22 | \ (s_ {y_i}) ^ {-2}\) ">20.66 | \ (w_i\) ">0.0234 |
| \ (C_ {std}\) (довільні одиниці виміру) ">0.500 | \ (S_ {std}\) (довільні одиниці виміру) ">60.42 | \ (s_ {std}\) ">0.33 | \ (s_ {y_i}) ^ {-2}\) ">9.18 | \ (w_i\) ">0.0104 |
Складання значень у четвертому стовпці дає
\[\sum_{i = 1}^{n} (s_{y_i})^{-2} \nonumber \]
які ми використовуємо для обчислення окремих ваг в останньому стовпці. Як перевірки на ваших розрахунках сума окремих ваг повинна дорівнювати числу калібрувальних нормативів, n. Сума записів в останньому стовпці дорівнює 6.0000, тому все добре. Після того, як ми обчислимо окремі ваги, ми використовуємо другу таблицю, щоб допомогти в обчисленні чотирьох термінів підсумовування в рівняннях для нахилу\(b_1\), і y -перехоплення,\(b_0\).
| \(x_i\) | \(y_i\) | \(w_i\) | \(w_i x_i\) | \(w_i y_i\) | \(w_i x_i^2\) | \(w_i x_i y_i\) |
|---|---|---|---|---|---|---|
| \ (x_i\) ">0.000 | \ (y_i\) ">0.00 | \ (w_i\) ">2.8339 | \ (w_i x_i\) ">0,0000 | \ (w_i y_i\) ">0,0000 | \ (w_i x_i^2\) ">0,0000 | \ (w_i x_i y_i\) ">0,0000 |
| \ (x_i\) ">0.100 | \ (y_i\) ">12,36 | \ (w_i\) ">2.8339 | \ (w_i x_i\) ">0.2834 | \ (w_i\) ">35.0270 | \ (w_i x_i^2\) ">0.0283 | \ (w_i x_i\) ">3.5027 |
| \ (x_i\) ">0,200 | \ (y_i\) ">24.83 | \ (w_i\) ">0.2313 | \ (w_i x_i\) ">0.0463 | \ (w_i\) ">5.7432 | \ (w_i x_i^2\) ">0,0093 | \ (w_i x_i\) ">1.1486 |
| \ (x_i\) ">0,300 | \ (y_i\) ">35.91 | \ (w_i\) ">0.0671 | \ (w_i x_i\) ">0.0201 | \ (w_i\) ">2.4096 | \ (w_i x_i^2\) ">0,0060 | \ (w_i x_i\) ">0.7229 |
| \ (x_i\) ">0,400 | \ (y_i\) ">48.79 | \ (w_i\) ">0.0234 | \ (w_i x_i\) ">0,0094 | \ (w_i\) ">1.1417 | \ (w_i x_i^2\) ">0.0037 | \ (w_i x_i\) ">0,4567 |
| \ (x_i\) ">0,500 | \ (y_i\) ">60.42 | \ (w_i\) ">0.0104 | \ (w_i x_i\) ">0,0052 | \ (w_i\) ">0.6284 | \ (w_i x_i^2\) ">0,0026 | \ (w_i x_i\) ">0.3142 |
Додавання значень в останніх чотирьох стовпцях дає
\[\sum_{i = 1}^{n} w_i x_i = 0.3644 \quad \sum_{i = 1}^{n} w_i y_i = 44.9499 \quad \sum_{i = 1}^{n} w_i x_i^2 = 0.0499 \quad \sum_{i = 1}^{n} w_i x_i y_i = 6.1451 \nonumber \]
який дає розрахунковий ухил і розрахунковий y -перехоплення як
\[b_1 = \frac {(6 \times 6.1451) - (0.3644 \times 44.9499)} {(6 \times 0.0499) - (0.3644)^2} = 122.985 \nonumber \]
\[b_0 = \frac{44.9499 - (122.985 \times 0.3644)} {6} = 0.0224 \nonumber \]
Рівняння калібрування
\[S_{std} = 122.98 \times C_{std} + 0.2 \nonumber \]
\(\PageIndex{31}\)На малюнку показана калібрувальна крива для зваженої регресії, визначеної тут, і калібрувальна крива для незваженої регресії. Хоча дві калібрувальні криві дуже схожі, є невеликі відмінності в нахилі та у -перехопленні. Найбільш примітно, що y -перехоплення для зваженої лінійної регресії ближче до очікуваного значення нуля. Оскільки стандартне відхилення для сигналу, S std, менше для менших концентрацій аналіту, C STD, зважена лінійна регресія надає більше уваги цим стандартам, що дозволяє краще оцінити y -перехоплення.
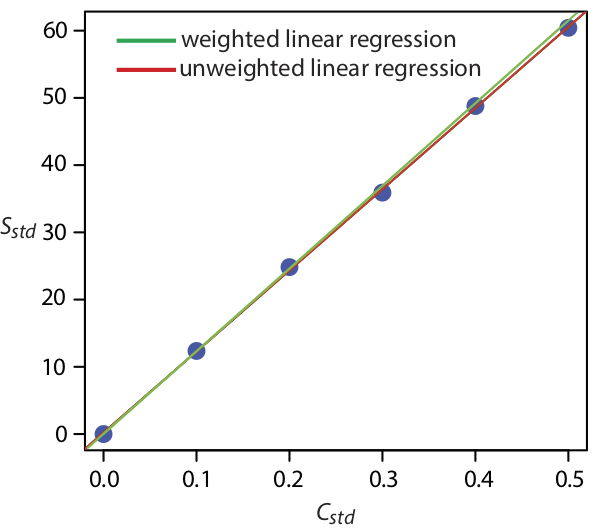
Рівняння для обчислення довірчих інтервалів для нахилу, y -перехоплення та концентрації аналіту при використанні зваженої лінійної регресії визначити не так просто, як для незваженої лінійної регресії [Bonate, P.J. Anal. Хім. 1993, 65, 1367—1372]. Однак довірчий інтервал для концентрації аналіта знаходиться на оптимальному значенні, коли сигнал аналіта знаходиться поблизу зважених центроїдів, y c, калібрувальної кривої.
\[y_c = \frac {1} {n} \sum_{i = 1}^{n} w_i x_i \nonumber \]
Зважена лінійна регресія з помилками в x та y
Якщо ми приберемо наше припущення, що невизначені помилки, що впливають на калібрувальну криву, присутні тільки в сигналі (y), то ми також повинні враховувати в регресійній моделі невизначені помилки, які впливають на концентрацію аналіта в стандартах калібрування (x). Рішення для результуючої лінії регресії більш задіяно, ніж для незважених або зважених ліній регресії. Хоча ми не будемо розглядати деталі в цьому підручнику, ви повинні знати, що нехтування наявністю невизначеної помилки в x може змістити результати лінійної регресії.
Див., наприклад, Комітет з аналітичних методів, «Встановлення лінійного функціонального зв'язку до даних з помилкою обох змінних», Технічний бриф КУА, березень 2002), а також додаткові ресурси цієї глави.
Криволінійна, багатоваріантна та багатоваріантна регресія
Прямолінійна регресійна модель, незважаючи на її очевидну складність, є найпростішим функціональним зв'язком між двома змінними. Що ми робимо, якщо наша калібрувальна крива криволінійна - тобто, якщо це крива, а не пряма? Один з підходів полягає в тому, щоб спробувати перетворити дані в пряму лінію. Таким чином були використані логарифми, експоненціальні, зворотні, квадратні корені та тригонометричні функції. Типовим прикладом є графік log (y) проти x. Такі перетворення не позбавлені ускладнень, з яких найбільш очевидним є те, що дані з рівномірною дисперсією в y не збережуть цю рівномірну дисперсію після її перетворення.
Тут варто відзначити, що термін «лінійний» не означає пряму. Лінійна функція може містити більше одного адитивного члена, але кожен такий термін має один і тільки один регульований мультиплікативний параметр. Функція
\[y = ax + bx^2 \nonumber \]
є прикладом лінійної функції, оскільки терміни x та x 2 містять один мультиплікативний параметр, a та b відповідно. Функція
\[y = x^b \nonumber \]
є нелінійним, оскільки b не є мультиплікативним параметром; це, натомість, потужність. Ось чому ви можете використовувати лінійну регресію, щоб пристосувати поліноміальне рівняння до ваших даних.
Іноді вдається перетворити нелінійну функцію в лінійну функцію. Наприклад, взяття журналу обох сторін нелінійної функції вище дає лінійну функцію.
\[\log(y) = b \log(x) \nonumber \]
Іншим підходом до розробки моделі лінійної регресії є пристосування поліноміального рівняння до даних, таких як\(y = a + b x + c x^2\). Ви можете використовувати лінійну регресію для обчислення параметрів a, b та c, хоча рівняння відрізняються від рівнянь для лінійної регресії прямої. Якщо ви не можете вмістити дані за допомогою одного поліноміального рівняння, можливо, можна встановити окремі поліноміальні рівняння до коротких відрізків калібрувальної кривої. Результатом є одна безперервна калібрувальна крива, відома як сплайн-функція. Використання R для криволінійної регресії включено в главу 8.5.
Детальніше про криволінійну регресію див. (а) Шараф, М.А.; Іллман, Д.Л.; Ковальський, Б.Р. хемометрика, Wiley-Interscience: Нью-Йорк, 1986; (б) Демінг, С.Н.; Морган, С.Л. Експериментальний дизайн: Хемометричний підхід, Elsevier: Амстердам, 1987.
Регресійні моделі в цьому розділі застосовуються лише до функцій, які містять одну залежну змінну та єдину незалежну змінну. Одним із прикладів є найпростіша форма закону Беера\(A\), в якій поглинання зразка на одній\(\lambda\) довжині хвилі залежить від концентрації одного аналіту,\(C_A\)
\[A_{\lambda} = \epsilon_{\lambda, A} b C_A \nonumber \]
де\(\epsilon_{\lambda, A}\) - молярна поглинання аналіта на обраній довжині хвилі та\(b\) довжина шляху через зразок. При наявності інтерферента, однак\(I\), сигнал може залежати від концентрацій як аналіту, так і інтерферентного
\[A_{\lambda} = \epsilon_{\lambda, A} b C_A + \epsilon_{\lambda, I} b C_I \nonumber \]
де\(\epsilon_{\lambda, I}\) - молярна абсорбційна здатність інтерферента, а C I - концентрація інтерферента. Це приклад багатоваріантної регресії, яка більш детально висвітлюється в Главі 9, коли ми розглянемо оптимізацію експериментів, де є одна залежна змінна і дві або більше незалежних змінних.
У багатоваріантній регресії ми маємо як кілька залежних змінних, таких як поглинання зразків на двох або більше довжині хвиль, так і кілька незалежних змінних, таких як концентрації двох або більше аналітів у зразках. Як обговорювалося в розділі 0.2, ми можемо представити це за допомогою матричних позначень
\[\begin{bmatrix} \cdots & \cdots & \cdots \\ \vdots & A & \vdots \\ \cdots & \cdots & \cdots \end{bmatrix}_{r \times c} = \begin{bmatrix} \cdots & \cdots & \cdots \\ \vdots & \epsilon b & \vdots \\ \cdots & \cdots & \cdots \end{bmatrix}_{r \times n} \times \begin{bmatrix} \cdots & \cdots & \cdots \\ \vdots & C & \vdots \\ \cdots & \cdots & \cdots \end{bmatrix}_{n \times c} \nonumber \]
де є\(r\) довжини хвиль,\(c\) зразки та\(n\) аналіти. Наприклад, кожен стовпець\(\epsilon b\) матриці містить\(\epsilon b\) значення для іншого аналіту на одній з\(r\) довжин хвиль, а кожен рядок\(C\) матриці - це концентрація одного з\(n\) аналітів в одному із\(c\) зразків. Більш докладно цей підхід ми розглянемо в главі 11.
Для приємного обговорення різниці між багатоваріантною регресією та багатоваріантною регресією див. Ідальго, Б.; Гудман, М. «Багатоваріантна або багатоваріантна регресія» Am. Громадська охорона здоров'я, 2013, 103, 39-40.
