19.1: Теорія ядерного магнітного резонансу

Як і у випадку з іншими формами оптичної спектроскопії, сигнал у спектроскопії ядерного магнітного резонансу (ЯМР) виникає внаслідок різниці рівнів енергії, зайнятих ядрами в аналіті. У цьому розділі ми розробляємо загальну теорію спектроскопії ядерного магнітного резонансу, яка спирається на квантову механіку та класичну механіку для пояснення цих енергетичних рівнів.

Квантовий механічний опис ЯМР

Квантово-механічний опис електрона задається чотирма квантовими числами: основним квантовим числом$n$, квантовим числом моменту моменту$l$, магнітним квантовим числом та спіновим квантовим числом$m_s$.$m_l$ Перші три з цих квантових чисел розповідають нам щось про те, де електрон відносно ядра і щось про енергію електрона. Останнє з цих чотирьох квантових чисел, спінове квантове число, говорить нам щось про здатність електрона взаємодіяти з прикладеним магнітним полем. Електрон має можливі спини +1/2 або -1/2, які ми часто називаємо обертанням вгору, використовуючи стрілку вгору$\uparrow$, щоб представити її, або як спина вниз, використовуючи стрілку вниз$\downarrow$, щоб представити його.

Ядро, як електрон, несе заряд і має спіновий квантове число. Загальний$I$ спін ядра є функцією кількості протонів і нейтронів, що складають ядро. Ось три простих правила для ядерних спінових станів:

• Якщо число нейтронів і кількість протонів обидва парні числа, то ядро не має спина; таким чином, ¹² С, з шістьма протонами і шістьма нейтронами, не має загального спина і$I = 0$.
• Якщо число нейтронів плюс кількість протонів є непарним числом, то ядро має напівціле спін, наприклад 1/2 або 3/2; таким чином, ¹³ С, з шістьма протонами і сімома нейтронами, має загальний спін$I = 1/2$; це також справедливо для ¹ H.
• Якщо число нейтронів і кількість протонів обидва непарні числа, то ядро має цілочисельний спін, такий як 1 або 2; таким чином, ² Н, з одним протоном і одним нейтроном, має загальний спін$I = 1$.

Примітка

Прогнозуючи, що ¹³ С має спін$I = 1/2$, але що ¹²⁷ Я має спін$I = 3/2$ і що ¹⁷ O має спін не$I = 5/2$ є тривіальним. Періодична таблиця, яка надає спінові стани для елементів, доступна тут.

Загальна кількість станів спина - тобто загальна кількість можливих орієнтацій спина - дорівнює$(2 \times I) + 1$. Щоб бути активним ЯМР, ядро повинно мати принаймні два спінові стани, щоб зміна спінових станів, а отже, і зміна енергії, можливо; таким чином, ¹² С, для яких існують$(2 \times 0) + 1 = 1$ спінові стани, є ЯМР неактивним, але ¹³ С, для яких існують$(2 \times 1/2) + 1 = 2$ спінові стани зі значеннями $m = +1/2$і з$m = -1/2$, ЯМР активний, як і ² Н, для яких існують$(2 \times 1) + 1 = 3$ спінові стани зі значеннями$m = +1/2$$m = 0$, і$m = -1/2$. Оскільки наш інтерес до цієї глави полягає в спектрах ЯМР для ¹ H і ¹³ C, ми обмежимося розглядом$I = 1/2$ і спином станів$m = +1/2$ і з$m = -1/2$.

Рівні енергії в прикладному магнітному полі

Припустимо, у нас велика популяція атомів ¹ Н. За відсутності застосованого магнітного поля атоми діляться порівну між можливими спіновими станами: 50% атомів мають спін +1/2, а 50% атомів мають спін -1/2. Обидва спінові стану мають однакову енергію, як це відбувається на лівій стороні малюнка$\PageIndex{1}$, і ні поглинання, ні випромінювання не відбувається.

Малюнок$\PageIndex{1}$. Діаграма енергетичного рівня для протона, ¹ Н, при відсутності (зліва) і при наявності (праворуч) прикладеного магнітного поля.

При наявності прикладеного магнітного поля, як на правій стороні малюнка$\PageIndex{1}$, ядра або вирівнюються з магнітним полем зі спинами$m = +1/2$, або вирівнюються по відношенню до магнітного поля спинами$m = -1/2$. Енергії в цих двох спінових станах,$E_\text{lower}$ і$E_\text{upper}$, задаються рівняннями

$$E_\text{lower} = - \frac{\gamma h}{4 \pi}B_0 \label{nmr1}$$

$$E_\text{upper} = + \frac{\gamma h}{4 \pi}B_0 \label{nmr2}$$

де$\gamma$ - магнітогирическое відношення для ядра,$h$ - постійна Планка, і$B_0$ - напруженість прикладеного магнітного поля. Різниця в енергії$\Delta E$, між двома станами є

$$\Delta E = E_\text{upper} - E_\text{lower} = + \frac{\gamma h}{4 \pi}B_0 - \left( - \frac{\gamma h}{4 \pi}B_0 \right) = \frac{\gamma h}{2 \pi}B_0 \label{nmr3}$$

Заміна рівняння\ ref {nmr3} у більш звичне рівняння$\Delta E = h \nu$ дає частоту електромагнітного випромінювання$\nu$, необхідну для зміни спінового стану як

$$\nu = \frac{\gamma B_0}{2 \pi} \label{nmr4}$$

Це називається частотою Лармора для ядра. Наприклад, якщо магніт має напруженість поля 11,74 Тесла, то частота, необхідна для здійснення зміни стану спина на ¹ Н, для чого$2.68 \times 10^8 \text{ rad}\text{ T}^{-1} \text{s}^{-1}$,$\gamma$ становить

$$\nu = \frac{(2.68 \times 10^8 \text{rad} \text{ T}^{-1}\text{s}^{-1})(11.74 \text{ T})}{2 \pi} = 5.01 \times 10^8 \text{ s}^{-1} \nonumber$$

або 500 МГц, що знаходиться в радіочастотному (РФ) діапазоні електромагнітного спектра. Це частота Лармора для ¹ H.

Населення Спін Стейтс

Відносна популяція верхнього$N_\text{upper}$ спінового стану та стану нижнього спина задається рівнянням Больцмана$N_\text{lower}$

$$\frac{N_\text{upper}}{N_\text{lower}} = e^{- \Delta E/k T} \label{nmr5}$$

де$k$ постійна Больцмана ($1.38066 \times 10^{-23} \text{ J/K}$) і$T$ температура в Кельвіні. Підстановка в рівняння\ ref {nmr3} для$\Delta E$ дає це співвідношення як

$$\frac{N_\text{upper}}{N_\text{lower}} = e^{-\gamma h B_0/2 \pi k T} \label{nmr6}$$

ЯКЩО помістити популяцію атомів ¹ Н в магнітне поле напруженістю 11,74 Тесла, то співвідношення$\frac{N_\text{upper}}{N_\text{lower}}$ при 298 К дорівнює

$$\frac{N_\text{upper}}{N_\text{lower}} = e^{-\frac{(2.68 \times 10^{8} \text{ rad} \text{ s}^{-1})(6.626 \times 10^{-34} \text{ Js})(11.74 \text{ T})}{(2 \pi)(1.38 \times 10^{-23} \text{ JK}^{-1})(298 \text{ K})}} = 0.99992 \nonumber$$

Якщо це співвідношення 1:1, то ймовірність поглинання і випромінювання рівні і немає чистого сигналу. При цьому різниця в популяціях становить близько 8 на 100 000, або 80 на 1 000 000, або 80 проміле. Невелика різниця в двох популяціях означає, що ЯМР менш чутливий, ніж багато інших спектроскопічних методів.

Класичний опис ЯМР

Щоб зрозуміти класичний опис експерименту ЯМР, ми спираємося на рис$\PageIndex{2}$. Для простоти припустимо, що в популяції доступних нам ядер спостерігається надлишок всього одного ядра зі спиновим станом +1/2. На малюнку ми бачимо$\PageIndex{2}a$, що спін цього ядра не ідеально вирівняний з прикладеним магнітним полем$B_0$, яке вирівняне з віссю z; замість цього ядро прецесує навколо осі z під кутом тета,$\Theta$. В результаті чистий магнітний момент по осі z,$\mu_z$, менше магнітного моменту, μ, ядра. Прецесія відбувається з кутовою швидкістю$\omega_0$, оф$\gamma B_0$.

Малюнок$\PageIndex{2}$. Ілюстрація, яка показує в (а) магнітний момент, μ, ядра, спина якого вирівнюється з нанесеним магнітним полем,$B_0$. Застосування магнітного поля,$B_1$ перевертає спин ядра, як показано в (б).

Якщо застосувати джерело радіочастотного (РФ) електромагнітного випромінювання вздовж осі х таким чином, що його компонент магнітного поля$B_1$, перпендикулярний$B_0$, то він буде генерувати власну кутову швидкість в xy -площині. Коли кутова швидкість попереджуючого ядра відповідає кутовій швидкості$B_1$, відбувається поглинання і обертання перевертається, як показано на малюнку$\PageIndex{2}b$.

Релаксація

Коли магнітне поле$B_1$ видаляється, ядро повертається в початковий стан, як видно на малюнку, процес$\PageIndex{2}a$, який називається релаксацією. При відсутності релаксації система насичується рівними популяціями двох спінових станів і поглинання наближається до нуля. Цей процес релаксації має два окремих механізми: спін-решітчаста релаксація і спін-спінова релаксація

При спін-решітчастої релаксації ядро в його вищому енергетичному спиновому стані$\PageIndex{2}b$, рис., повертається до свого нижчого енергетичного стану стану спина$\PageIndex{2}a$, Фігура, шляхом передачі енергії іншим видам, присутнім у зразку (решітка в спін-решітці). Релаксація спін-решітки характеризується експоненціальним розпадом першого порядку з характерним часом релаксації$T_1$, який є мірою середнього часу перебування ядра в його вищому енергетичному спіновому стані. Менші значення для отримання$T_1$ більш ефективної релаксації.

Якщо два ядра одного типу, але в різних спінових станах, знаходяться в безпосередній близькості один від одного, вони можуть торгувати місцями, в яких ядро в вищому енергетичному спиновому стані віддає свою енергію ядру в стані нижчого енергетичного спина. Результатом є зменшення середньої тривалості життя збудженого стану. Це називається спін-спін релаксації і він характеризується час релаксації$T_2$.

Безперервна хвиля ЯМР проти перетворення Фур'є ЯМР

У розділі 16 ми дізналися, що можемо записувати інфрачервоний спектр за допомогою скануючого монохроматора для проходження послідовно різних довжин хвиль ІЧ-випромінювання через зразок, отримуючи спектр поглинання як функцію довжини хвилі. Ми також дізналися, що ми можемо отримати той самий спектр, пропускаючи всі довжини хвиль ІЧ-випромінювання через зразок одночасно за допомогою інтерферометра, а потім використовувати перетворення Фур'є для перетворення отриманої інтерферограми в спектр поглинання як функція довжини хвилі. Тут розглядаються їх еквіваленти для ЯМР-спектроскопії.

Безперервна хвиля ЯМР

Якщо ми скануємо,$B_1$ утримуючи$B_0$ постійну - або скануємо,$B_0$ утримуючи$B_1$ постійну, то ми можемо визначити частоти Лармора, де поглинає певне ядро. Результатом є спектр ЯМР, який показує інтенсивність поглинання як функцію частоти, на якій відбувається це поглинання. Оскільки ми записуємо спектр шляхом сканування через континуум частот, метод відомий як безперервна хвиля ЯМР. Рисунок$\PageIndex{2}$ надає корисну візуалізацію для цього експерименту.

Перетворення Фур'є ЯМР

При перетворенні Фур'є ЯМР магнітне поле$B_1$ застосовується як короткий імпульс радіочастотного (РЧ) електромагнітного випромінювання, зосередженого на частоті, відповідній ядру цікавить і для сили первинного магнітного поля,$B_0$. Імпульс зазвичай становить 1-10 мкс в довжину і застосовується в xy -площині. З принципу невизначеності Гейзенберга короткий імпульс$\Delta t$ призводить до широкого діапазону частот як$\Delta f = 1/\Delta t$; це гарантує, що імпульс охоплює достатній діапазон частот, такий, що цікавить нас ядро поглинає енергію і увійде в збуджений стан.

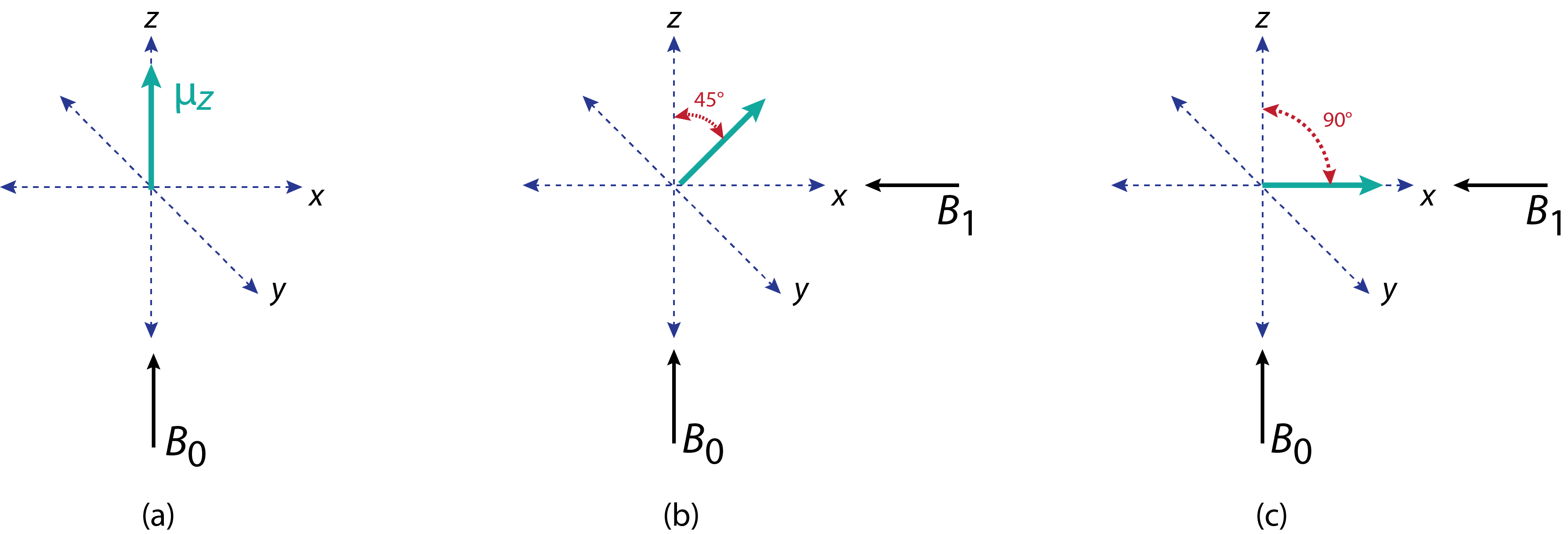
Перед тим як застосувати імпульс, популяція ядер вирівнюється паралельно прикладеному магнітному полю$B_0$, деякі зі спіном +1/2 і інші зі спіном -1/2. Як ми дізналися вище, існує невеликий надлишок ядер зі спинами +1/2, які ми можемо представити як єдиний вектор, який показує їх комбіновані магнітні моменти уздовж осі z$\mu_z$, як показано на малюнку$\PageIndex{3}a$. Коли ми застосовуємо імпульс радіочастотного електромагнітного випромінювання з напруженістю магнітного поля$B_1$, спінові стани кінчика ядер віддаляються від осі z на кут,$\gamma$ який залежить від магнітогиричного співвідношення ядра$B_1$, значення та довжини імпульсу. Якщо, наприклад, імпульс 5 мкс кінчає магнітний вектор на 45° (рис.$\PageIndex{3}b$), то імпульс 10 мкс перекине магнітний вектор на 90° градусів (рис.$\PageIndex{3}c$), так що він тепер повністю лежить в межах xy -площині.

Малюнок$\PageIndex{3}$. Ілюстрація, яка показує (а) чистий магнітний момент на осі z для популяції ядер у прикладному магнітному полі з напруженістю поля$B_0$. Застосування імпульсного радіочастотного поля$B_1$, нахиляє магнітний момент (b) від осі z. Чим довше імпульс РФ, тим більший кут перекидання, як показано в (с).

Після закінчення пульсу ядра починають розслаблятися назад в початковий стан. $\PageIndex{4}$На малюнку видно, що це розслаблення відбувається як в xy -площині (спін-спінова релаксація), так і по осі z (спін-решітка релаксації). Якби ми простежили шлях магнітного вектора з часом, ми побачили б, що він слідує за спіралеподібним рухом, оскільки його внесок у площину xy зменшується, а його внесок вздовж осі z збільшується. Ми вимірюємо цей сигнал - званий вільним індукційним розпадом, або FID - протягом цього періоду розслаблення.

Малюнок$\PageIndex{4}$. Ілюстрація, що показує процес релаксації під час експерименту ЯМР. У нижньому ряду показаний чистий магнітний момент, вирівняний з віссю z$\mu_z$, як функція часу. У верхньому рядку показаний чистий магнітний момент у xy -площині з малюнком у верхньому правому куті, що показує загальну зміну чистого магнітного моменту у трьох вимірах.

FID для системи, яка складається лише з одного типу ядра, - це простий експоненціально загасаючий коливальний сигнал на малюнку$\PageIndex{5}a$. Перетворення Фур'є цього простого FID дає спектр на малюнку$\PageIndex{5}b$, який має один пік. Зразок з більш ніж одним типом ядра дає більш складну схему FID, таку як на малюнку$\PageIndex{5}c$, і більш складний спектр, такий як два піки на малюнку$\PageIndex{5}d$. Зауважте, що, як ми дізналися в попередній обробці перетворення Фур'є в главі 7, більш широкий пік у частотній області призводить до більш швидкого занепаду в часовій області.

Малюнок$\PageIndex{5}$. Панелі (a) і (b) показують сигнал FID для зразка, який дає один пік і результат прийняття FT FID. Панелі (c) і (d) показують сигнал FID для зразка, який складається з двох піків і результат прийняття FT FID.

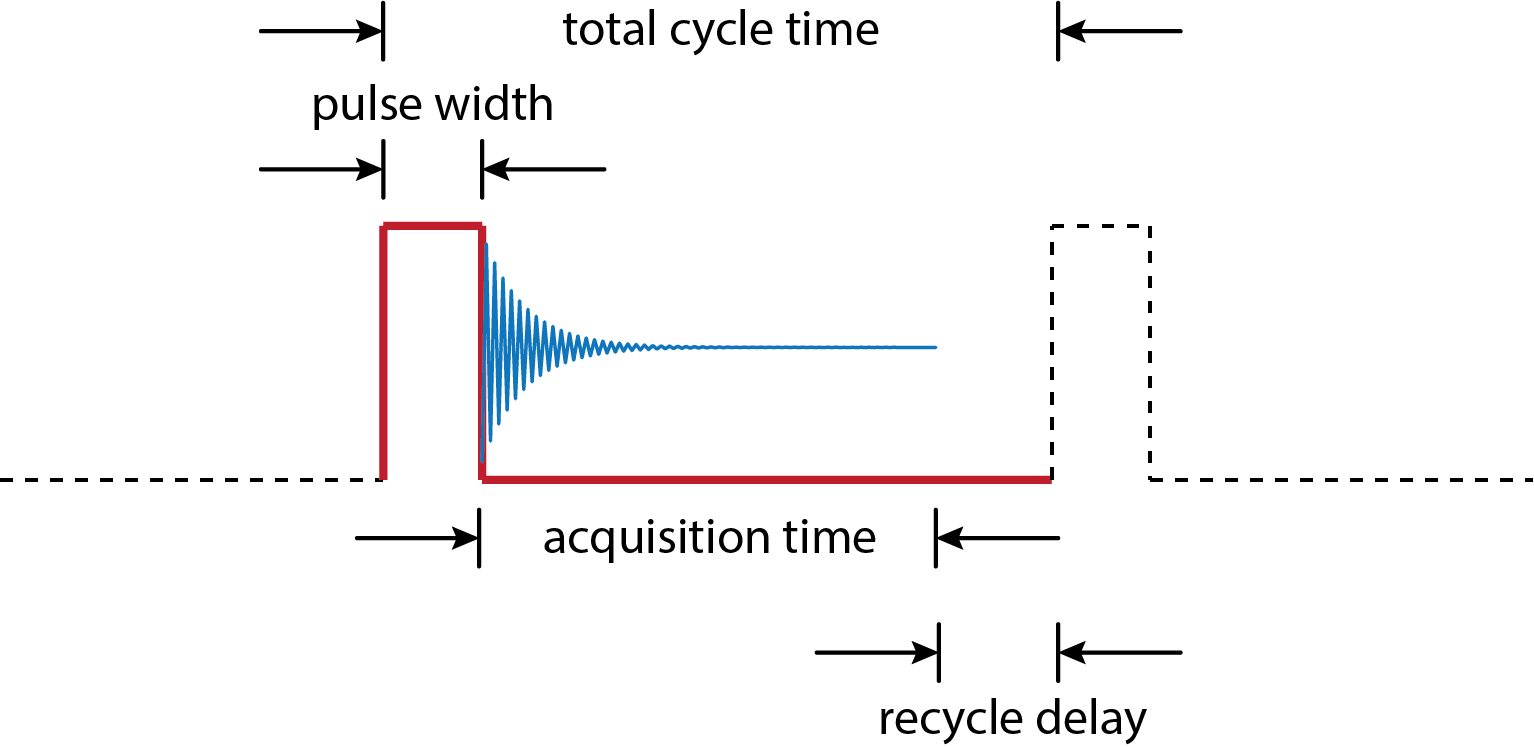
$\PageIndex{6}$На малюнку показана типова послідовність імпульсів, що виділяє загальний час циклу та його складові частини: ширину імпульсу, час збору, протягом якого фіксується FID, і затримку рециркуляції перед застосуванням наступного імпульсу та початком наступного циклу.

Малюнок$\PageIndex{1}$: Приклад послідовності імпульсів.