18.1: Теорія спектроскопії комбінаційного випромінювання
- Page ID
- 27508
Синій колір неба вдень і червоний колір сонця на заході - результат розсіювання світла дрібними частинками пилу, молекулами водяної пари, іншими газами в атмосфері. Ефективність розсіяння фотона залежить від його довжини хвилі. Ми бачимо небо синім протягом дня, тому що фіолетове і синє світло розсіюються більшою мірою, ніж інші, довші довжини хвиль світла. З тієї ж причини сонце виглядає червоним на заході сонця, оскільки червоне світло розсіюється менш ефективно і швидше проходить через атмосферу, ніж інші довжини хвиль світла. Якщо ми посилаємо сфокусований монохроматичний промінь випромінювання з довжиною хвилі\(\lambda\) через середовище частинок - будь то тверді частинки або окремі молекули - які мають розміри\(<1.5 \lambda\), то випромінювання розсіюється у всіх напрямках. Наприклад, інфрачервоне світло в ближньому ІК з довжиною хвилі 700 нм буде розсіюватися від будь-якої частинки, найбільший розмір якої менше 1300 нм. Навіть в інакше прозорому зразку відбувається розсіювання від молекул.
Раман Спектра
Існує два загальних класи розсіяння: пружне розсіювання і непружне розсіювання. При пружному розсіюванні фотон спочатку поглинається частинкою, а потім випромінюється без зміни її енергії (\(\Delta E = 0\)); це називається розсіюванням Релея. При нееластичному розсіюванні фотон спочатку поглинається частинкою, а потім випромінюється зі зміною її енергії (\(\Delta E \ne 0\)); це називається розсіюванням Рамана. Сюжет, який показує інтенсивність розсіяного випромінювання як функцію енергії розсіяного фотона, вираженої у вигляді зміни хвильового числа\(\Delta \overline{\nu}\), називається спектром комбінаційного випромінювання і величини\(\Delta \overline{\nu}\) називаються комбінаційними зміщеннями.
\(\PageIndex{1}\)На малюнку показана частина спектру комбінаційного випромінювання для тетрахлорметану вуглецю і ілюструє кілька важливих особливостей. По-перше, Rayleigh розсіювання виробляє інтенсивний пік в\(\Delta \overline{\nu} = 0\). Хоча пік інтенсивний, він не несе корисної інформації, оскільки абсолютна енергія - це саме те, що для джерела. По-друге, розсіювання Рамана має дві складові - лінії Стокса та лінії проти Стокса - які мають однакові абсолютні зрушення щодо лінії для розсіювання Релея, але мають різні ознаки. Лінії Стокса мають позитивні значення для,\(\Delta\overline{\nu}\) а лінії проти Стокса мають від'ємні значення для\(\Delta \overline{\nu}\). По-третє, кожна з ліній Стокса більш інтенсивна, ніж відповідна лінія АнтиСтокса. По-четверте, оскільки ми вимірюємо зсув хвильового пікучисла щодо вихідного випромінювання, спектр не залежить від випромінювання джерела.
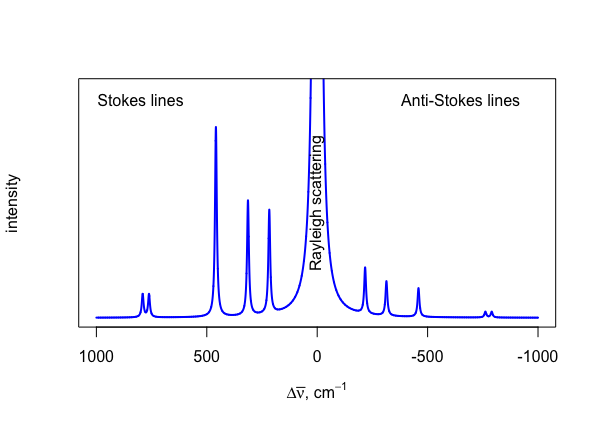
Енергія - і, таким чином, хвильова кількість - фотона, який відчуває розсіювання Стокса, менша, ніж енергія - і, таким чином, хвильове число - випромінювання джерела, що ставить питання про те, чому зсув Стокса повідомляється як позитивне значення замість негативного значення. Хоча ви знайдете більшість спектрів Рамана з позитивними значеннями для зсуву Стокса, ви також знайдете приклади, коли зрушення Стокса повідомляються з негативними значеннями. Оскільки лінії Стокса є більш інтенсивними, ніж лінії Анти-Стокса, і, отже, більш корисними, і тому, що їх відповідні зрушення виникають внаслідок тих самих змін коливальних енергетичних станів, які ми знаходимо в ІЧ-спектроскопії, зручно повідомляти лінії Стокса як позитивні значення, щоб ми могли вирівняти Раманові та ІЧ-спектри видів. Див. Наступні два розділи для отримання додаткової інформації.
Механізм розсіяння Рамана і Релея
У главі 6 ми розглянули механізм, за допомогою якого відбувається поглинання і емісія. У наступних розділах ми досліджували атомно-абсорбційну та атомно-емісійну спектрометрію, ультрафіолетову та видиму молекулярну абсорбційну спектрометрію, спектрометрію молекулярної люмінесценції та ін У кожному випадку ми починали з розгляду діаграми рівня енергії, яка пояснює походження поглинання та викиду. На малюнку\(\PageIndex{2}\) представлена енергетична діаграма, яку ми можемо використовувати для пояснення походження ліній, що складають спектр Рамана, наприклад, спектр для тетрахлорметану вуглецю на малюнку\(\PageIndex{1}\).
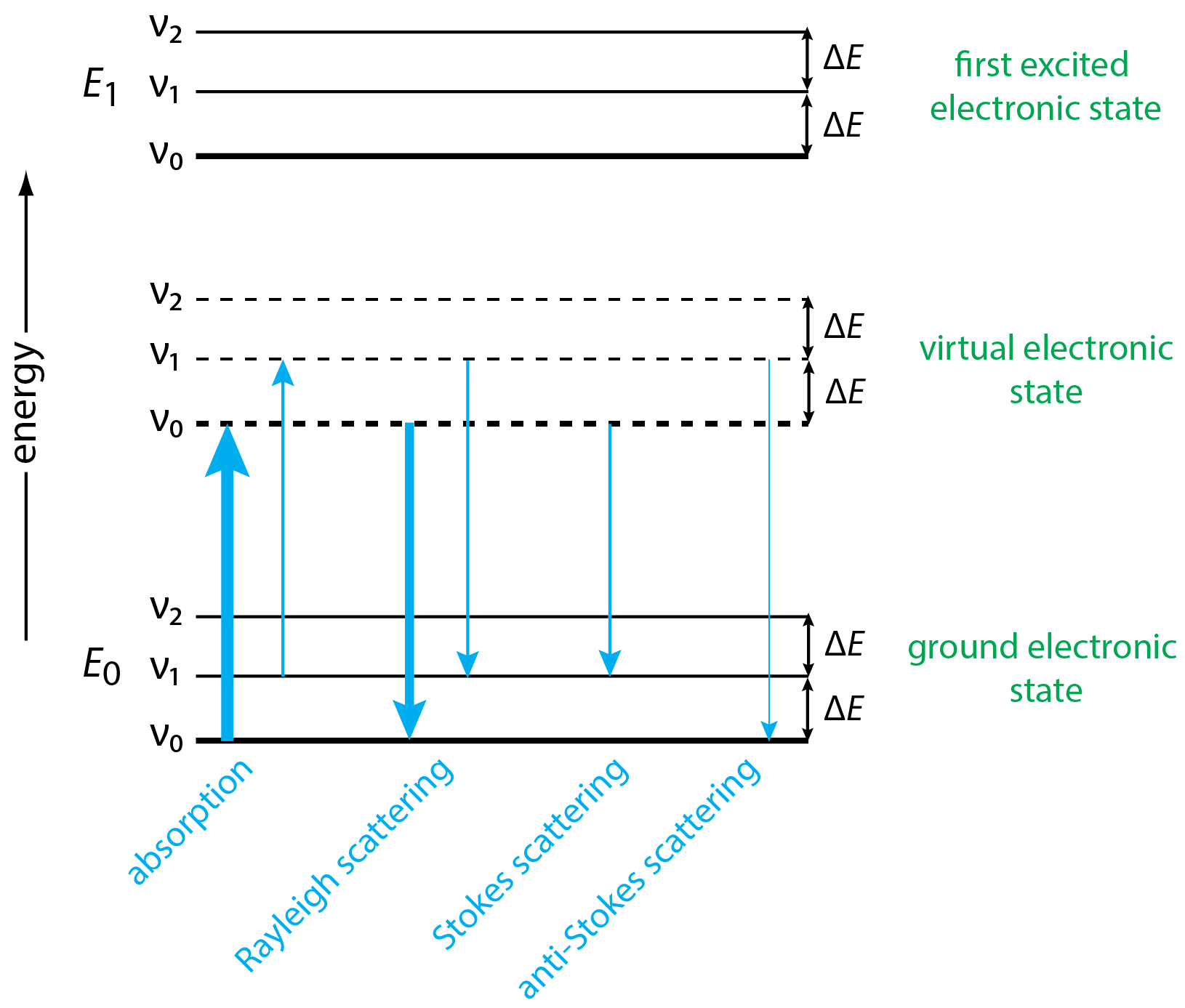
Перше, що слід зазначити про діаграму рівня енергії на малюнку,\(\PageIndex{2}\) це те, що, крім показу наземного електронного стану та першого збудженого електронного стану - кожен з трьома коливальними енергетичними рівнями - він також показує віртуальний електронний стан, щось, з чим ми не стикалися з іншими методами (див. , наприклад, енергетична діаграма для ультрафіолетової та ІЧ-спектрометрії молекулярного поглинання (на рис. 6.4.2). Земля і перші збуджені електронні стани квантуються, а це означає, що поглинання не може статися, якщо енергія джерела не відповідає точно зміні енергії між двома електронними станами. Енергія випромінюваного фотона також фіксується різницею в енергії двох електронних станів. Віртуальний електронний стан, однак, не квантується і визначається енергією випромінювання джерела. Джерело випромінювання, отже, не потрібно відповідати певній зміні енергії.
Поглинання фотона вихідного випромінювання переміщує аналіт з наземного електронного стану у віртуальний електронний стан без зміни коливального енергетичного стану, як видно двома стрілками в крайньому лівому куті діаграми. Оскільки наземний коливальний енергетичний стан є більш населеним\(\nu_0\), ніж стан вібраційної енергії\(\nu_1\), більше аналіту потрапляє в найнижчу вібраційну енергію віртуального електронного стану, ніж у вищому стані вібраційної енергії, що показано тут відносною товщиною двох стрілки.
Опинившись у віртуальному електронному стані, аналіт може повернутися в наземне збуджене стан одним з трьох способів. Це може зробити без зміни рівня вібраційної енергії. При цьому енергія поглинання і енергія емісії однакові і\(\Delta E = 0\) і\(\Delta \overline{\nu} = 0\). Це розсіювання Релея і, як підказує комбінована товщина двох стрілок на малюнку\(\PageIndex{2}\), це найважливіший механізм розслаблення.
Коли релаксація включає зміну коливального енергетичного рівня, результатом є абсолютна зміна енергії, еквівалентна різниці енергії\(\Delta E\), між сусідніми коливальними енергетичними рівнями. Для розсіювання Стокса розслаблення - це більш високий рівень вібраційної енергії, такий як\(\nu_0 \rightarrow \nu_1\) і, для розсіювання проти Стокса, розслаблення до нижчого рівня вібраційної енергії, наприклад\(\nu_1 \rightarrow \nu_0\). Як припускає товщина ліній для розсіювання Стокса та Анти-Стокса на малюнку\(\PageIndex{2}\), лінії Стокса є більш інтенсивними, ніж лінії Анти-Стокса, оскільки вони починаються в більш густонаселеному збудженому стані.
Взаємозв'язок між ІЧ-і Рамановим спектрами
Однією з важливих особливостей\(\PageIndex{2}\) Figure є те, що перехід, який породжує певну лінію Стокса або лінію Анти-Стокса, є тим самим переходом, який дасть початок відповідному ІЧ-діапазону. Якщо правила вибору для цих переходів однакові для конкретного виду, то ми очікуємо, що його ІЧ-спектр і його Рамановий спектр матимуть піки при однакових (або подібних) значеннях\(\overline{\nu}\) і\(\Delta \overline{\nu}\) для його фундаментальних коливань; однак, як ми бачимо в таблиці\(\PageIndex{1}\) для вуглецю тетрахлорид, cCl 4, в його спектрі Рамана є п'ять основних коливань, але лише три в його ІЧ-спектрі.
| Інфрачервоний (\(\overline{\nu}\), см —1) | Раман (\(\Delta \overline{\nu}\), см —1) |
|---|---|
| \ (\ overline {\ nu}\), см—1) ">— | \ (\ Delta\ overline {\ nu}\), см—1) ">217.0 (l) |
| \ (\ overline {\ nu}\), см—1) ">309.9 (л) слабкий | \ (\ Delta\ overline {\ nu}\), см—1) ">313.5 (l) |
| \ (\ overline {\ nu}\), см—1) ">— | \ (\ Delta\ overline {\ nu}\), см—1) ">458.7 (l) |
| \ (\ overline {\ nu}\), см—1) ">768 (g); дуже сильний | \ (\ Delta\ overline {\ nu}\), см—1) ">761.7 (l) |
| \ (\ overline {\ nu}\), см—1) ">789 (g); дуже сильний | \ (\ Delta\ overline {\ nu}\), см—1) ">790.4 (l) |
| \ (\ Delta\ overline {\ nu}\), cm—1) ">Позначення (g) та (l) вказують на фазу зразка, де (g) - газова фаза, а (l) - рідка фаза. Позначення слабких і дуже сильних для ІЧ піків вказують на відносну ступінь поглинання: дуже сильне означає відносно невеликий% T (і сильне поглинання), а слабкий означає відносно великий% T (і слабке поглинання). Див. Рисунок\(\PageIndex{1}\) щодо відносної величини розсіяння в спектрі комбінаційного розсіювання для cCl 4. | |
У розділі 16 ми дізналися, що в ІЧ-спектроскопії фундаментальна вібраційна енергія сполуки активна - тобто ми бачимо пік в його ІЧ-спектрі - тільки якщо відповідне розтягнення або вигин призводить до зміни дипольного моменту сполуки. Для спектроскопії комбінаційного випромінювання фундаментальна вібраційна енергія сполуки активна лише в тому випадку, якщо відповідне розтягнення або вигин призводить до зміни поляризуваності його електронів. Поляризуваність, по суті, є мірою того, наскільки легко спотворювати електронну хмару сполуки, застосовуючи зовнішнє електричне поле, наприклад, коли поглинається фотон від джерела; загалом, поляризуваність збільшується, коли рух розтягування або згинання збільшує об'єм сполуки, оскільки електрони потім розподілити по більшій кількості простору.
\(\PageIndex{3}\)На малюнку показані чотири режими розтягування та згинання для cCl 4. Рух розтягування в (a), при якому всі чотири довжини зв'язку C—Cl збільшуються і зменшуються разом, означає, що об'єм молекули збільшується і зменшується; таким чином, цей коливальний режим є активним раманом. Симетрія руху розтягування, однак, означає, що дипольний момент молекули не змінюється, а коливальний режим є ІЧ-неактивним. Асиметрична розтяжка в (b), з іншого боку, є активною як ІЧ, так і раманською. Рух згинання в (c) призводить до того, що молекула стає більш-менш компактною за розміром і є активним раманом; симетрія ножичних рухів, однак, означає, що вібраційний режим є ІЧ-неактивним. Рухи згинання в (d) як ІЧ, так і Раманові активні.
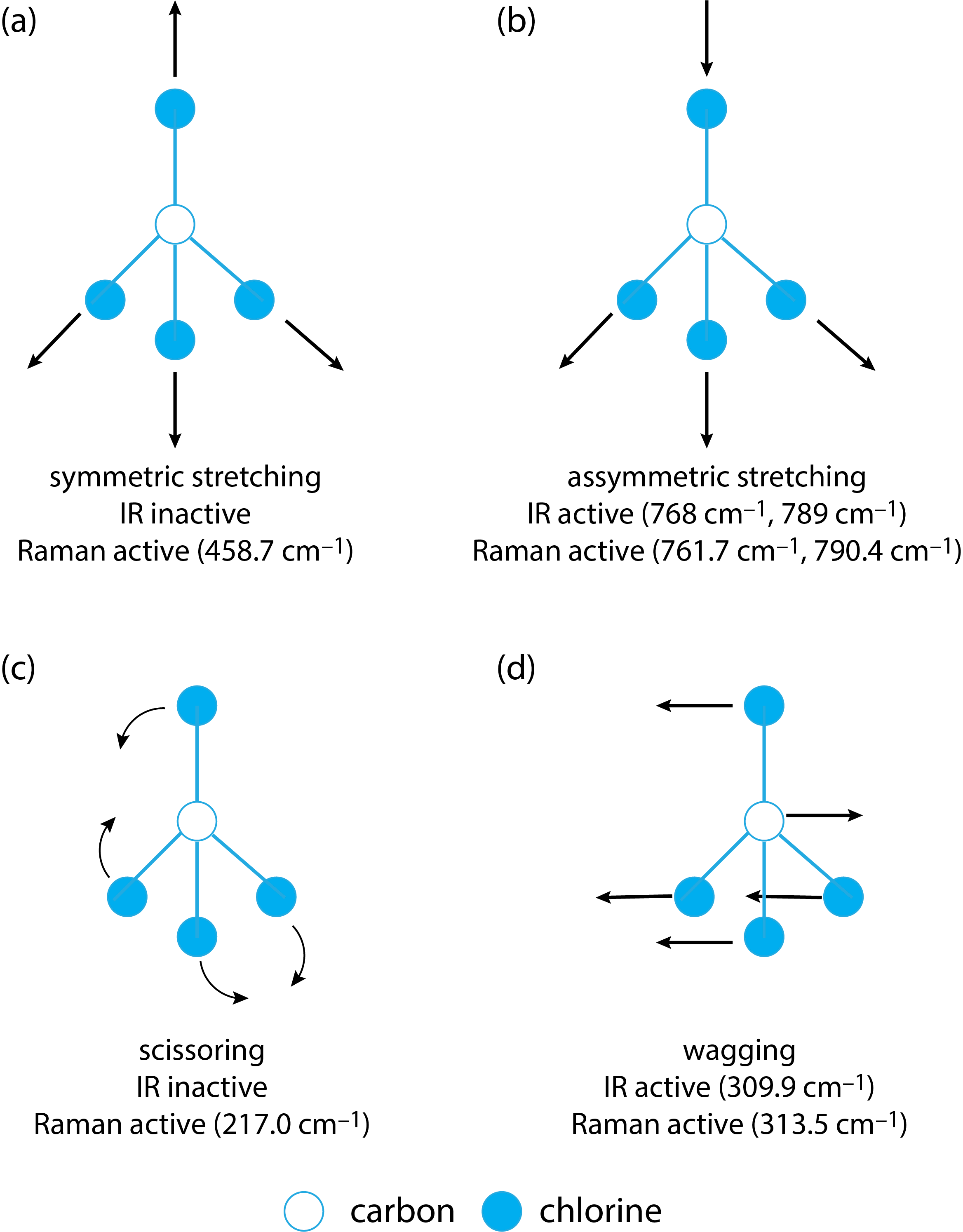
Загалом, симетричні режими розтягування та згинання призводять до відносно сильних піків розсіяння Рамана, але відсутність поглинання в ІК, тоді як симетричні режими розтягування та вигину призводять як до ІК, так і Раманових піків. В результаті ІК і Раман є взаємодоповнюючими прийомами.
Коефіцієнти деполяризації Рамана
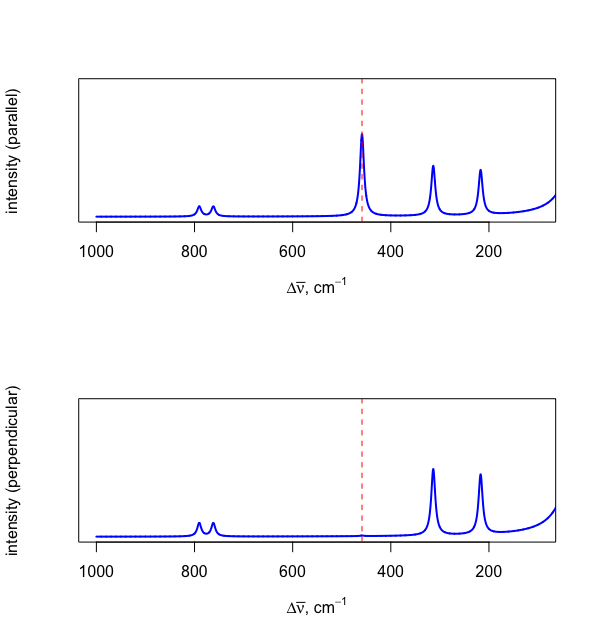
Якщо джерело електромагнітного випромінювання плоскополяризоване, то зібрати Рамановский спектр можна за допомогою світла, розсіяного в площині, яка паралельна джерелу і окремо в площині, яка перпендикулярна джерелу. Ставлення інтенсивності розсіяння лінії в перпендикулярному спектрі\(I_{\perp}\), до інтенсивності розсіювання в паралельному спектрі\(I_{||}\), називається коефіцієнтом деполяризації,\(p\).
\[p = \frac{I_{\perp}}{I_{||} } \label{depolarization} \]
Раманова лінія, яка походить від коливального режиму, який не змінює форму молекул, призведе до коефіцієнта деполяризації, близького до нуля, і відсутності лінії в перпендикулярному спектрі. \(\PageIndex{4}\)На малюнку показаний спектр Рамана при зборі даних паралельно (зверху) і перпендикулярно (знизу) до джерела світла. Відсутність піку в 458,7 см —1 в перпендикулярному спектрі підтверджує, що це симетрична розтяжка, проілюстрована на рис\(\PageIndex{3}a\).