12.1: Основоположні принципи
- Page ID
- 26971
У главі 6 ми ввели електромагнітний спектр та характерні властивості фотонів, такі як довжини хвиль, частоти та енергії ультрафіолетового, видимого та інфрачервоного світла. Діапазон довжин хвиль для фотонів рентгенівського випромінювання простягається приблизно від 0,01 нм до 10 нм. Хоча ми звикли повідомляти про довжину хвилі фотона в нанометрах, з історичних причин довжина хвилі рентгенівського фотона зазвичай повідомляється в ангстремах (для яких символ Å) де 1 Å = 0,1 нм; таким чином, діапазон довжин хвиль від 0.01 нм до 10 нм для рентгенівського випромінювання також виражається як 0.1 Å до 100 Å. Цей діапазон довжин хвиль відповідає діапазону частот від приблизно\(3 \times 10^{19} \text{ s}^{-1}\) до\(3 \times 10^{16} \text{ s}^{-1}\), і діапазону енергій від\(2 \times 10^{-19} \text{ J}\) до\(2 \times 10^{-17} \text{ J}\).
Джерела рентгенівських променів
Існує три рутинні способи генерування рентгенівських променів, кожен з яких розглядається в цьому розділі: ми можемо бомбардувати відповідний метал пучком високоенергетичних електронів, ми можемо використовувати один рентген для стимуляції випромінювання додаткових рентгенівських променів через флуоресценцію, і ми можемо використовувати радіоактивний ізотоп, який випромінює рентгенівські промені як це розпадається.
Отримання рентгенівських променів з джерел електронного пучка
Електронний пучок створюється шляхом нагрівання вольфрамової дротяної нитки до температури, при якій вона випускає електрони. Ці електрони тягнуться до металевої мети, застосовуючи прискорюючу напругу між металевою мішенню та вольфрамовим дротом. Результатом є широкий континуум рентгенівського випромінювання на рис\(\PageIndex{1}\). Джерелом цього безперервного спектра випромінювання є зменшення кінетичної енергії електронів при їх зіткненні з металевою мішенню. Втрата кінетичної енергії призводить до виробництва фотонів у широкому діапазоні довжин хвиль і відома як Bremsstrahlung, або гальмівне випромінювання.
У попередніх розділах ми розділили джерела фотонів на дві широкі групи: безперервні джерела, такі як вольфрамова лампа, які виробляють фотони на всіх довжині хвиль між нижньою межею та верхньою межею, і лінійні джерела, такі як лампа з порожнистим катодом, які виробляють фотони для однієї або декількох дискретних довжин хвиль. Джерела, що використовуються для генерації рентгенівських променів, також генерують континуальні та/або лінійні спектри.
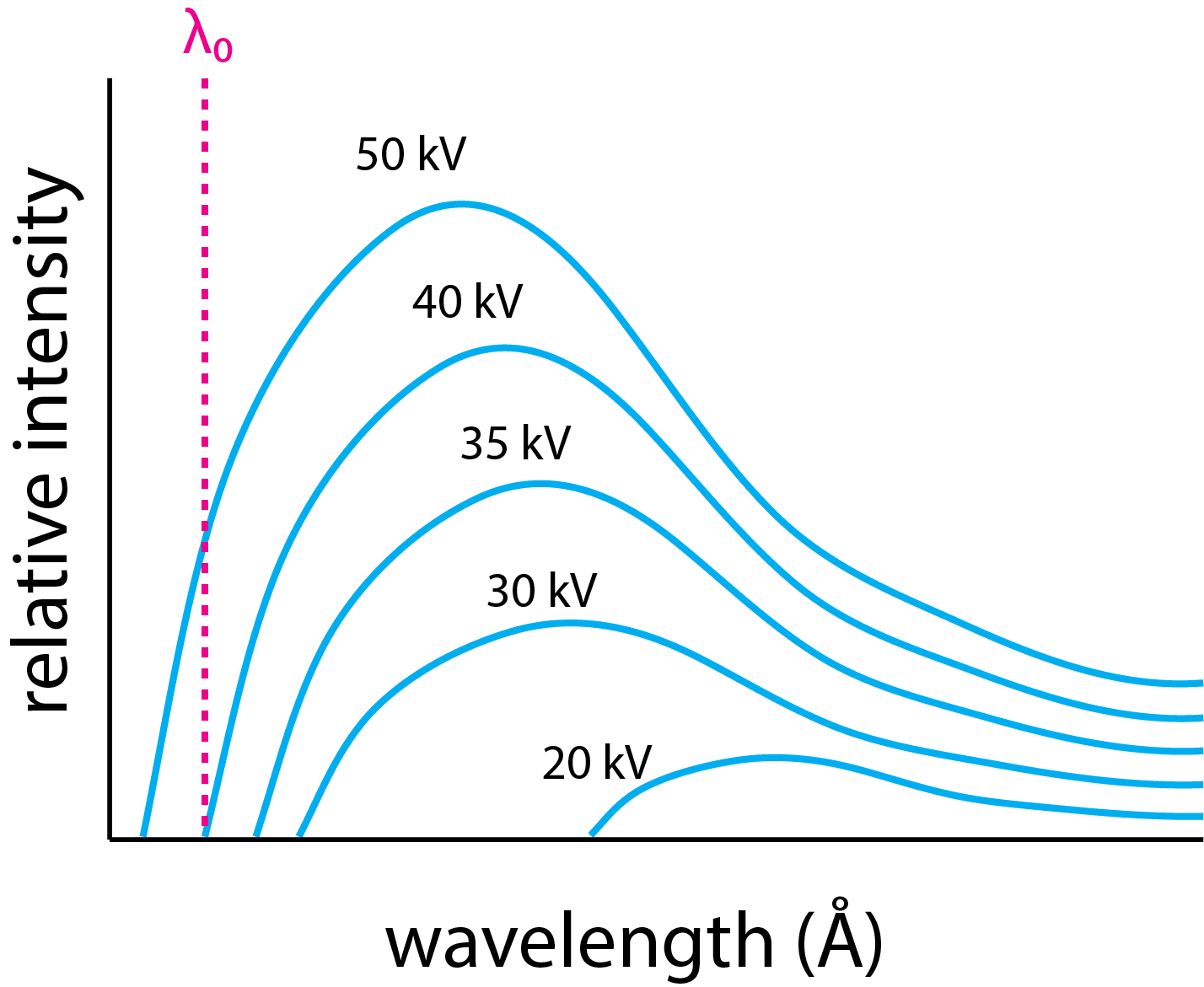
Нижня межа довжини хвилі для рентгенівського випромінювання\(\lambda_0\), визначена тут як, є максимально можливою втратою кінетичної енергії, КЕ, і дорівнює
\[KE = \frac{hc}{\lambda_0} = Ve \label{lmin} \]
де h - постійна Планка, c - швидкість світла, V - розгінна напруга, а е - заряд на електроні. Твір розгінної напруги і заряду на електроні - кінетична енергія електронів. Розв'язування рівняння\ ref {lmin} для\(\lambda_0\) дає
\[\lambda_0 = \frac{hc}{Ve} = \frac{12.398 \text{ kV Å}}{V} \label{lambdamin2} \]
де\(\lambda_0\) знаходиться в ангстремах, а V - в кіловольтах. Зверніть увагу, що Equation\ ref {lmin} і Equation\ ref {lambdamin2} не містять жодних термінів, які залежать від цільового металу, а\(\lambda_0\) це означає, що для будь-якого прискорювального напруги однакове для всіх металевих мішеней. Таблиця\(\PageIndex{1}\) дає значення\(\lambda_0\) цього діапазону прискорювальних напруг на рис\(\PageIndex{1}\).
| розгінна напруга (кВ) | \(\lambda_0\)(Å) |
|---|---|
| 20 | \ (\ лямбда_0\) (Å) ">0.62 |
| 25 | \ (\ лямбда_0\) (Å) ">0.50 |
| 30 | \ (\ лямбда_0\) (Å) ">0.41 |
| 35 | \ (\ лямбда_0\) (Å) ">0.35 |
| 40 | \ (\ лямбда_0\) (Å) ">0.31 |
| 45 | \ (\ лямбда_0\) (Å) ">0.28 |
| 50 | \ (\ лямбда_0\) (Å) ">0.25 |
Якщо застосувати досить велике прискорює напруга, то спектр випромінювання буде складатися як з континуального спектра, так і з лінійного спектра, як ми бачимо на малюнку\(\PageIndex{2}\) з молібденом в якості цільового металу. Спектр складається як з континууму, подібного до того\(\PageIndex{1}\), що на малюнку, і двох ліній, один на довжині хвилі 0.63 Å і один на довжині хвилі 0.71 Å. Джерелом цих ліній є випромінювання рентгенівських променів від збуджених іонів стану, які утворюються, коли досить високоенергетичний електрон з електронного пучка видаляє електрон з атомної орбіти, близької до ядра. Оскільки електрони в атомних орбіталах на більшій відстані від ядра падають в атомну орбіталь з вакансією, вони виділяють свою додаткову енергію у вигляді фотона.
Хоча фонове випромінювання з континууму однакове для всіх металевих цілей, енергія для ліній має значення, характерні для різних металів, оскільки енергія видалення електрона змінюється від елемента до елемента, збільшуючи з атомним номером. Наприклад, прискорює напруга не менше
\[V = \frac{12.398 \text{ kV Å}}{0.61 Å} = 20 \text{ kV} \nonumber \]
потрібен для генерації лінійного спектра для молібдену на рис\(\PageIndex{2}\).
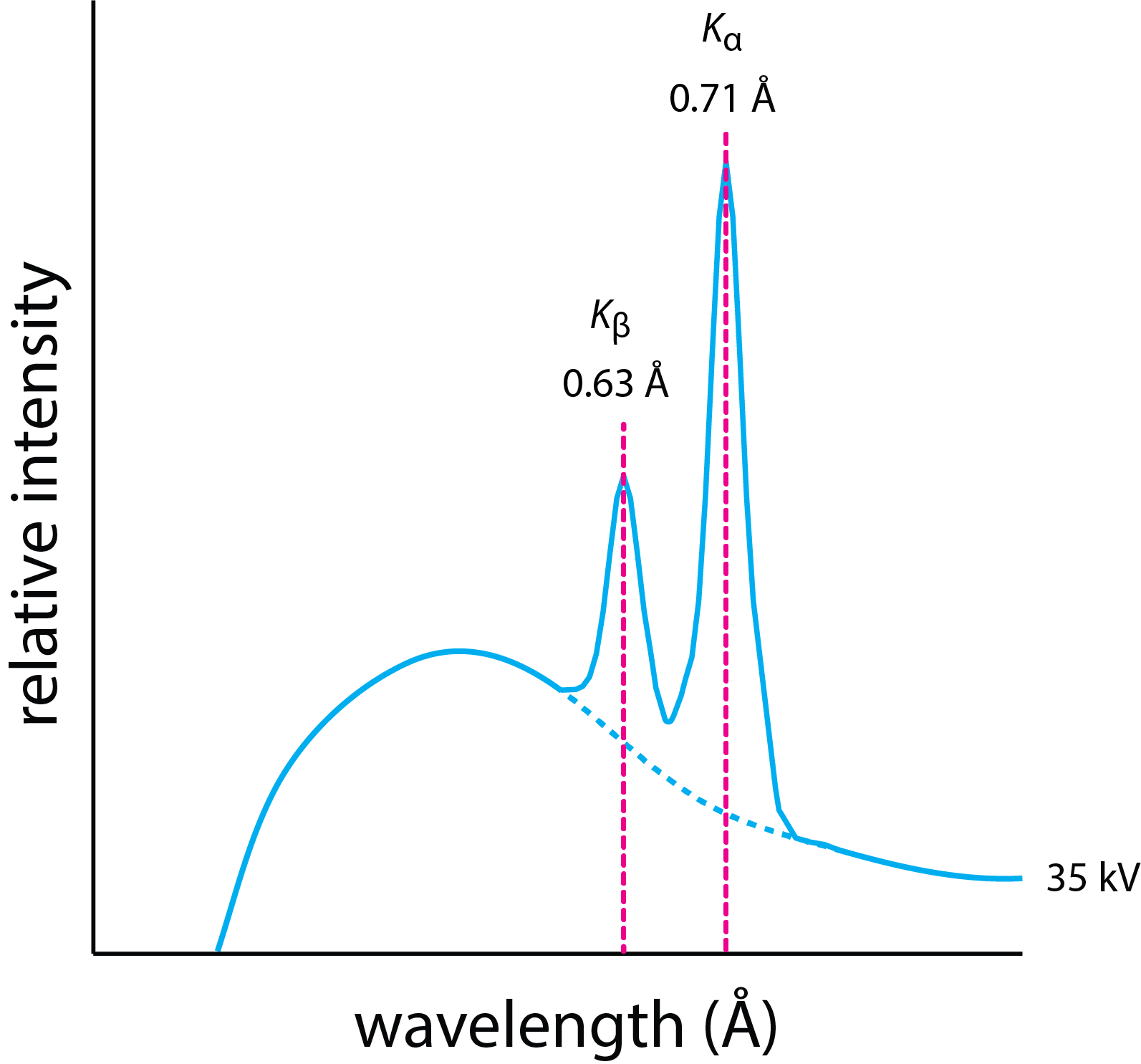
Характерні емісійні лінії для молібдену на малюнку\(\PageIndex{2}\) ідентифікуються як\(K_{\alpha}\) і\(K_{\beta}\), позначення, з якими ви, можливо, не знайомі. Спрощена діаграма енергетичного рівня на малюнку\(\PageIndex{3}\) допоможе нам зрозуміти це позначення. Кожна стрілка на цій діаграмі енергетичного рівня показує перехід, при якому електрон рухається від орбіти на більшу відстань від ядра до орбіти ближче до ядра. Букви K, L і M відповідають основному квантовому числу n, яке має значення 1, 2, 3..., які вказують на початкову вакансію, створену зіткненням пучка іонів з цільовим металом. Грецькі символи\(\alpha\)\(\beta\), і\(\gamma\) вказують джерело електрона, який заповнює цю вакансію з точки зору його зміни в основному квантовому числі,\(\Delta n\). Електрон, що рухається від n = 2 до n = 1 і електрон, що рухається від n = 4 до n = 3, мають однакове позначення\(\alpha\). Лінія емісії на малюнку\(K_{\beta}\),\(\PageIndex{2}\) визначена як, отже, є результатом переміщення електрона в оболонці n = 3 в вакансію в оболонці n = 1\(K\).
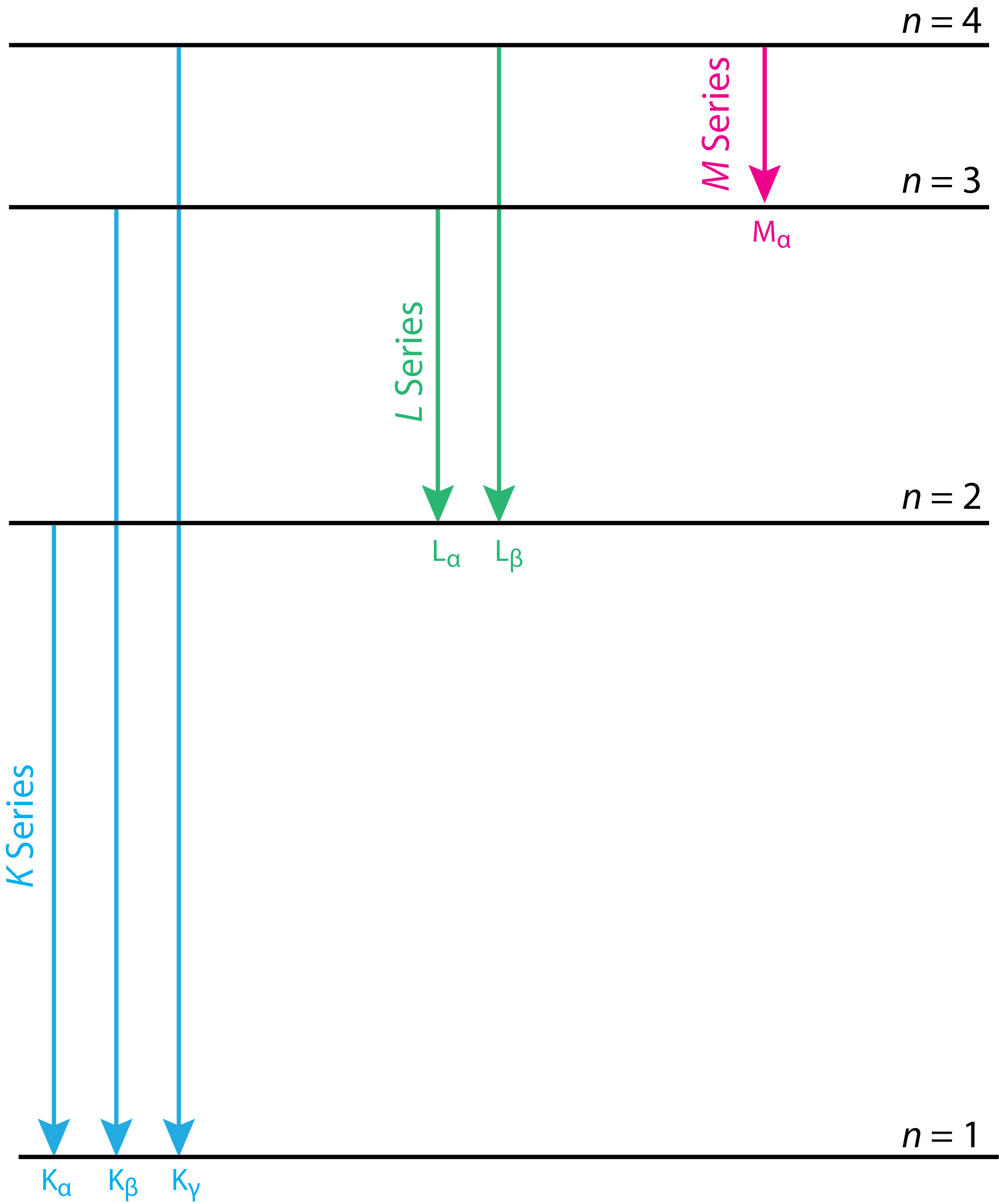
Чому Figure є\(\PageIndex{3}\) спрощеною діаграмою рівня енергії? Для кожного n > 1 існує більше однієї атомної орбіти. При n = 2 існує три енергетичні рівні: один, який відповідає l = 0, той, який відповідає l = 1 і m l = 0, і той, який відповідає l = 1 і m l = ±1. Допустимі переходи на рівні енергії n = 1 вимагають зміни значення для l; таким чином, ми очікуємо знайти дві емісійні лінії від n = 2 до n = 1 замість тієї, яка показана на малюнку\(\PageIndex{3}\). Ці дві лінії, які ми можемо ідентифікувати як\(\text{K}_{\alpha 1}\) і\(\text{ K}_{\alpha 2}\), як правило, досить близькі за значенням, щоб вони не вирішені в спектрі випромінювання рентгенівського випромінювання. Наприклад,\(\text{K}_{\alpha 1} = 0.709\) і\(\text{ K}_{\alpha 2} = 0.714\) для молібдену. Ви можете знайти таблицю ліній рентгенівського випромінювання тут.
Отримання рентгенівських променів з флуоре
Коли атом в збудженому стані випромінює фотон як засіб повернення в більш низький енергетичний стан, то як ми описуємо процес, залежить від джерела енергії, який створив збуджений стан. Коли збудження є результатом теплової енергії, ми називаємо процес атомної емісії. Коли збудження є результатом поглинання фотона, ми називаємо процес атомної флуоресценції. У рентгенівській флуоресценції збудження здійснюється за допомогою фотонів від джерела безперервного рентгенівського випромінювання. Детальніше про рентгенівську флуоресценцію наведено далі в цьому розділі.
Отримання рентгенівських променів з радіоактивних джерел
Атоми, які мають однакову кількість протонів, але різну кількість нейтронів, є ізотопами. Для ідентифікації ізотопу ми використовуємо позначення\({}_Z^A E\), де E - атомний символ елемента, Z - атомний номер елемента, а A - номер атомної маси елемента. Хоча різні ізотопи елемента мають однакові хімічні властивості, їх ядерні властивості не ідентичні. Найголовніша відмінність ізотопів - їх стабільність. Ядерна конфігурація стабільного ізотопу залишається постійною з часом. Нестабільні ізотопи, однак, розпадаються спонтанно, виділяючи частинки радіоактивного розпаду, коли вони перетворюються в більш стабільну форму.
Атомний номер елемента, Z, дорівнює числу протонів і його атомна маса, A, дорівнює сумі кількості протонів і нейтронів. Ми представляємо ізотоп вуглецю-13 як\(_{6}^{13} \text{C}\) тому, що вуглець має шість протонів і сім нейтронів. Іноді ми опускаємо Z з цього позначення - ідентифікація елемента, а атомний номер повторюється, оскільки всі ізотопи вуглецю мають шість протонів, а будь-який атом, який має шість протонів, є ізотопом вуглецю. Таким чином, 13 С і С—13 є альтернативними позначеннями для цього ізотопу вуглецю.
Радіоактивні частинки можуть розпадатися декількома способами, один з яких призводить до випромінювання рентгенівських променів. Наприклад, 55 Fe може захоплювати електрон і піддаватися процесу, при якому протон стає нейтроном, стаючи 55 Мп і вивільняючи надлишкову енергію у вигляді\(\text{K}_{\alpha}\) рентгенівського випромінювання. Ми не будемо далі розглядати радіоактивні джерела атомного рентгенівського випромінювання; однак, див. Главу 32 для подальшого обговорення радіоактивних методів аналізу.
X-Ray поглинання
\(\PageIndex{4}\)На малюнку показана частина спектру поглинання рентгенівського випромінювання молібдену в тому ж діапазоні довжин хвиль, як показано\(\PageIndex{2}\) на малюнку для його спектру випромінювання. Обидва спектри відносно прості: спектр випромінювання складається з двох ліній, накладених на континуумний фон, а спектр поглинання складається з однієї лінії, ідентифікованої тут як ребро K.
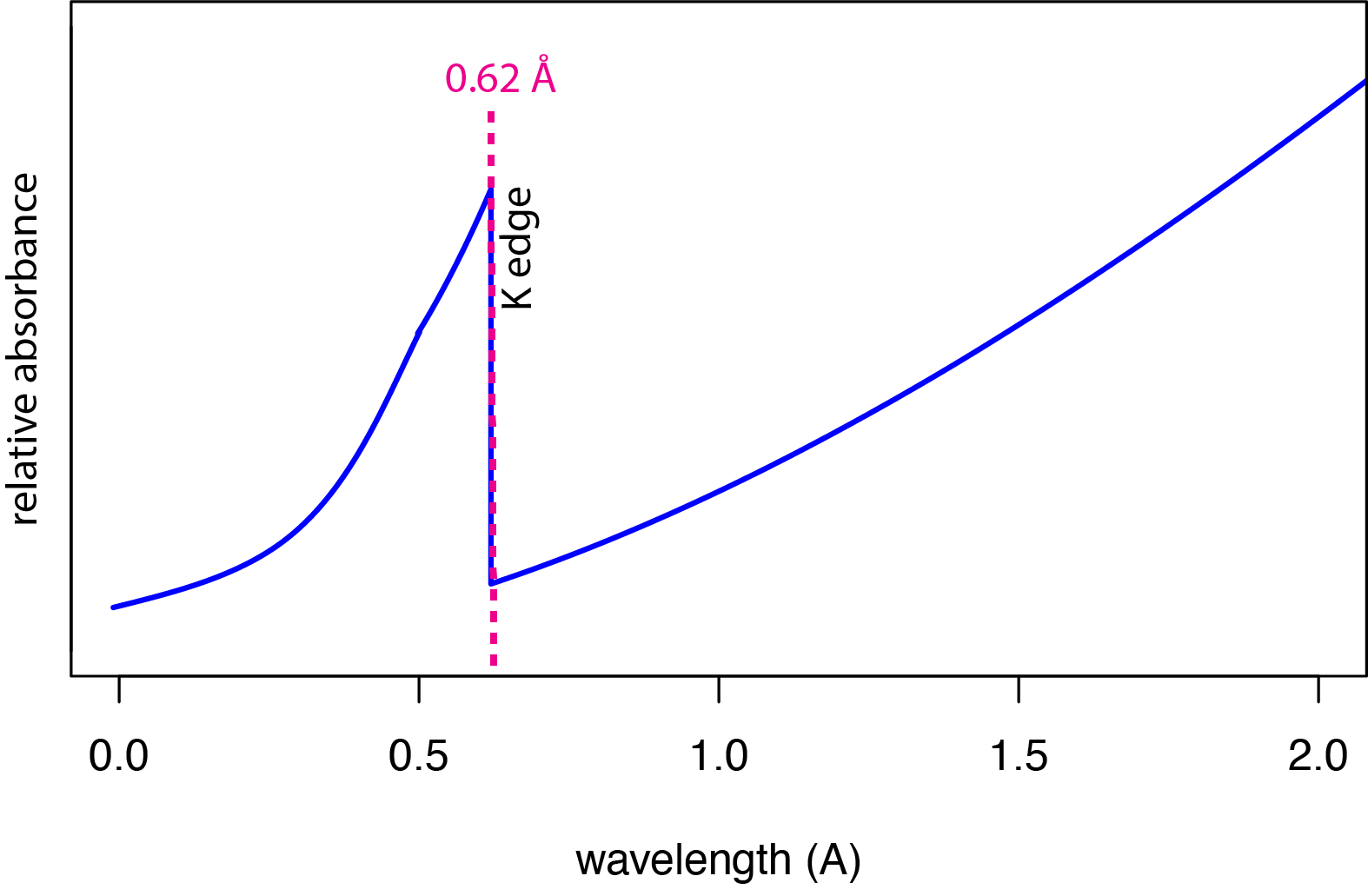
Процес поглинання
Якщо рентгенівський фотон має достатню енергію, то його поглинання атомом призводить до викиду електрона з однієї з внутрішніх атомних орбіталей атома, яку ви можете визнати як виробництво фотоелектрона. Для молібдену необхідна довжина хвилі 0,62 Å (енергія 20,0 кВ) для викиду фотоелектрона з оболонки К (n = 1). На цій довжині хвилі ймовірність поглинання знаходиться на найбільшій. На більш коротких довжині хвиль (більших енергіях) є достатня енергія для викиду електрона, однак ймовірність поглинання зменшується, а відносне поглинання зменшується повільно. Різке зменшення поглинання для довжин хвиль, більших за 0,62 Å—це різке зменшення є джерелом терміна «край» - відбувається тому, що фотони більше не мають достатньої енергії для викиду електрона з оболонки K. Повільне зростаюче поглинання на довжині хвиль, більших за ребро K, є результатом викиду електронів з оболонки L, яка має ребра на 4,3 Å, 4,7 Å та 4,9 Å.
Спрощена діаграма рівня енергії в\(\PageIndex{3}\) показує лише один рівень енергії для n = 2 (оболонка L). Як ми вже зазначали раніше, існує три енергетичних рівня, коли n = 2: той, який відповідає l = 0, той, який відповідає l = 1 і m l = 0, і той, який відповідає l = 1 і м л = ± 1. Три ребра, що відповідають цим енергетичним рівням, ідентифікуються як L I, L II та L III.
Закон пива та поглинання рентгенівського випромінювання
Коли джерело рентгенівських променів проходить через зразок товщиною x, проводиться наступне рівняння
\[A = -\ln \frac{P}{P_0} = \mu_{\text{M}} \rho x \label{beerxray} \]
де A - поглинання,\(P_0\) потужність джерела рентгенівського випромінювання, що падає на зразок,\(P\) - потужність джерела рентгенівського випромінювання після того, як він проходить через зразок,\(\mu_{\text{M}}\) є коефіцієнтом поглинання маси зразка і\(\rho\) щільність зразка. Можливо, ви помітили подібність між цим рівнянням та рівнянням закону Біра, з яким ми вперше зіткнулися в главі 6
\[A = -\ln \frac{P}{P_0} = \epsilon b C \label{beer} \]
де\(\epsilon\) молярна абсорбційна здатність,\(b\) - довжина шляху, і\(C\) молярна концентрація. Зверніть увагу, що як щільність (г/мл), так і молярність (моль/л) є мірою концентрації, яка виражає кількість поглинаючого матеріалу, присутнього в зразку.
X-Ray флуоресценція
Коли електрон викидається з оболонки поблизу ядра шляхом поглинання рентгенівського випромінювання, створена вакансія з часом заповнюється, коли електрон на більшій відстані від ядра рухається вниз. Оскільки для викидання електрона і створення вакансії потрібно більше енергії, ніж повертається рухом інших електронів у вакансію, результуюче флуоресцентне випромінювання рентгенівських променів завжди знаходиться на довжині хвиль, які довші (менша енергія), ніж довжина хвилі, яка була поглинена. Ми бачимо це на малюнку\(\PageIndex{4}\) та малюнку\(\PageIndex{1}\) для молібдену, де він поглинає рентген з довжиною хвилі 0.62 Å і випромінює рентгенівські промені з довжинами хвиль 0.63 Å і 0.71 Å.
Рентгенівська дифракція
Коли рентгенівський промінь фокусується на зразку, який має регулярну (кристалічну) картину атомів у трьох вимірах, частина випромінювання розсіюється з поверхні, а частина випромінювання проходить через наступний шар атомів, де триває комбінація розсіювання і проходження. В результаті цього процесу випромінювання зазнає дифракції, в якій рентгенівські промені деяких довжин хвиль відображаються від поверхні, тоді як рентгенівські промені інших довжин хвиль цього не роблять. Умови, які призводять до дифракції, легко зрозуміти, використовуючи діаграму на рис\(\PageIndex{5}\).
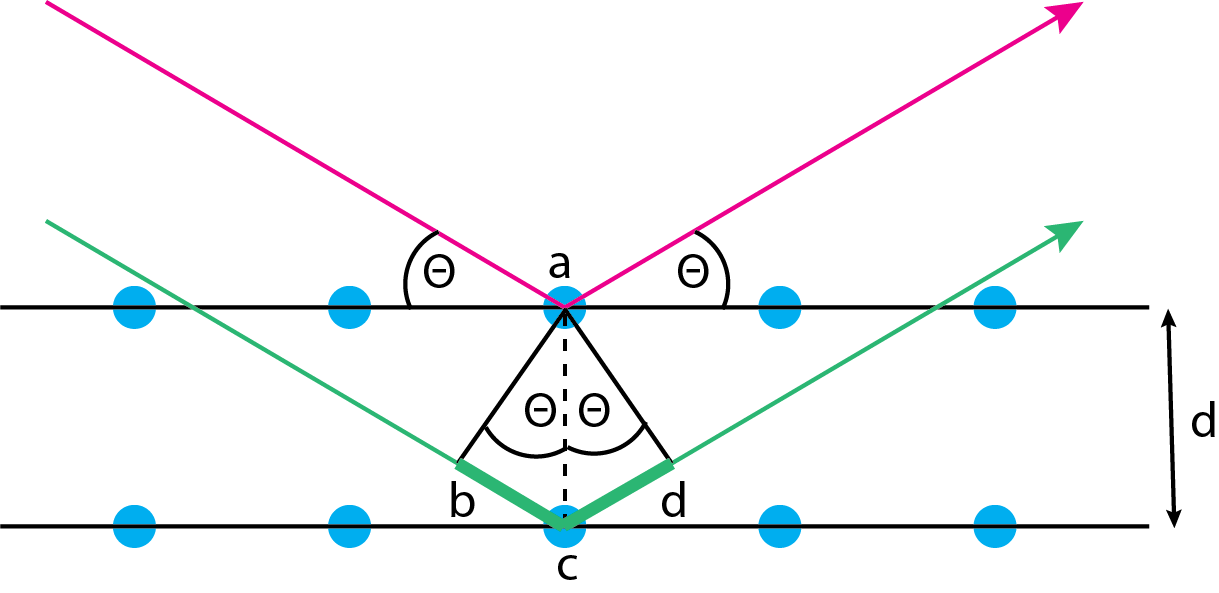
Червоні та зелені стрілки - це два паралельних пучка рентгенівських променів, які зосереджені на впорядкованому кристалічному твердому тілі, що складається з шаруватого повторюваного малюнка атомів, показаного синіми колами. Два пучка рентгенівських променів стикаються з твердим тілом під кутом\(\theta\). Рентген, показаний червоним кольором, розсіює від першого шару, виходячи під тим же кутом\(\theta\). Рентген, показаний зеленим кольором, проникає до другого шару, де він піддається розсіюванню, виходячи під тим же кутом\(\theta\). Ми знаємо з суперпозиції хвиль (див. Розділ 6), що два пучки рентгенівських променів залишаться у фазі і, таким чином, відчувають конструктивні перешкоди, лише якщо додаткова відстань, пройдена зеленою хвилею - сума відрізків лінії\(\overline{bc}\) і\(\overline{cd}\) - є цілим числом кратним довжині хвилі; таким чином
\[\overline{bc} + \overline{cd} = n \lambda \label{bragg1} \]
Ми також знаємо, що довжина відрізків лінії\(\overline{bc}\) і\(\overline{cd}\) задаються
\[\overline{bc}= \overline{cd} = d \sin \theta \label{bragg2} \]
де\(d\) - відстань між шарами кристала. Поєднання рівняння\ ref {bragg1} та рівняння\ ref {bragg2} дає
\[n \lambda = 2 d \sin \theta \label{bragg3} \]
Перестановка рівняння\ ref {bragg3} показує, що ми будемо спостерігати дифракцію тільки під кутами, які задовольняють рівнянню
\[\sin \theta = \frac{n \lambda}{2d} \label{bragg4} \]
