5.3: Покращення сигналу-шум
- Page ID
- 26920
Існує два широких підходи, які ми можемо використовувати для покращення співвідношення сигнал/шум: апаратний та програмний. Апаратні підходи вбудовуються в прилад і включають рішення про те, як прилад налаштований на проведення вимірювань (наприклад, вибір швидкості сканування або ширини щілини), і як сигнал обробляється приладом (наприклад, за допомогою електронних фільтрів). Тут коротко розглянуто декілька підходів, інші включені до обговорення окремих інструментів. Програмні рішення - це обчислювальні підходи, в яких ми маніпулюємо даними або під час їх збору, або після завершення збору даних.
Апаратні рішення
Одним із способів зменшення шуму є зосередження уваги на схемі, або апаратному забезпеченні, використовуваному для вимірювання сигналу.
Екранування
Одним із способів зменшення шуму навколишнього середовища є запобігання його потраплянню в електронну схему приладу. Одним із підходів є використання клітки Фарадея, в якій прилад сидить у приміщенні або просторі, покритому провідним матеріалом. Електромагнітне випромінювання з навколишнього середовища поглинається провідним матеріалом, а потім шунтується на землю. Замість того, щоб укладати весь інструмент у клітку Фарадея, особливо чутливі частини схеми можуть бути екрановані.
Диференційний підсилювач
Різницевий підсилювач (див. Розділ 3) - це електрична схема, яка використовується для визначення різниці між двома вхідними напругами або струмами та повернення цієї різниці як більшої напруги або струму. Оскільки величина шуму у двох вхідних сигналах, як правило, подібна за значенням - тобто вона знаходиться у фазі - тоді як сигнал, що цікавить, значна частина внеску шуму у сигнал віднімається.
Фільтрація
Коли частота шуму сильно відрізняється від частоти сигналу, проста електрична схема може бути використана для видалення високочастотного шуму та передачі низькочастотного сигналу; це називається фільтром низьких частот. Докладніше про фільтри низьких частот див. розділ 2.
Модуляція
Коли цікавить сигнал має низьку частоту, ефект мерехтіння шуму стає значним, оскільки техніка, яка видаляє низькочастотний шум, також видалить сигнал. Модуляція - це процес збільшення частоти сигналу. По завершенні для видалення шуму використовується фільтр високих частот. Реверсування модуляції повертає вихідний сигнал, але з більшою частиною шуму видалено.
Програмні рішення
У цьому розділі ми розглянемо три поширених обчислювальних інструменту для поліпшення співвідношення сигнал/шум: усереднення сигналу, цифрове згладжування і фільтрація Фур'є.
Усереднення сигналу
Найголовніша відмінність між сигналом і шумом полягає в тому, що сигнал є визначальним (фіксованим за значенням), а шум - невизначеним (випадковим за значенням). Якщо ми вимірюємо чистий сигнал кілька разів, ми очікуємо, що його значення буде однаковим кожен раз; Таким чином, якщо ми додамо разом n сканів, ми очікуємо, що чистий сигнал\(S_n\), визначається як
\[S_n = n S \nonumber \]
де\(S\) сигнал для одноразового сканування. Оскільки шум є випадковим, його значення змінюється від одного запуску до іншого, іноді зі значенням, яке більше, а іноді зі значенням, яке менше, а іноді зі значенням, яке є позитивним, а іноді і з негативним значенням. В середньому стандартне відхилення шуму збільшується, оскільки ми робимо більше сканування, але це робить це повільніше, ніж для сигналу
\[s_n = \sqrt{n} s \nonumber \]
де\(s\) - стандартне відхилення для одного сканування і\(s_n\) стандартне відхилення після n сканувань. Поєднання цих двох рівнянь показує нам,\(S/N\) що відношення сигнал/шум після n сканувань збільшується як
\[(S/N)_n = \frac{S_n}{s_n} = \frac{nS}{\sqrt{n}s} = \sqrt{n}(S/N)_{n = 1} \nonumber \]
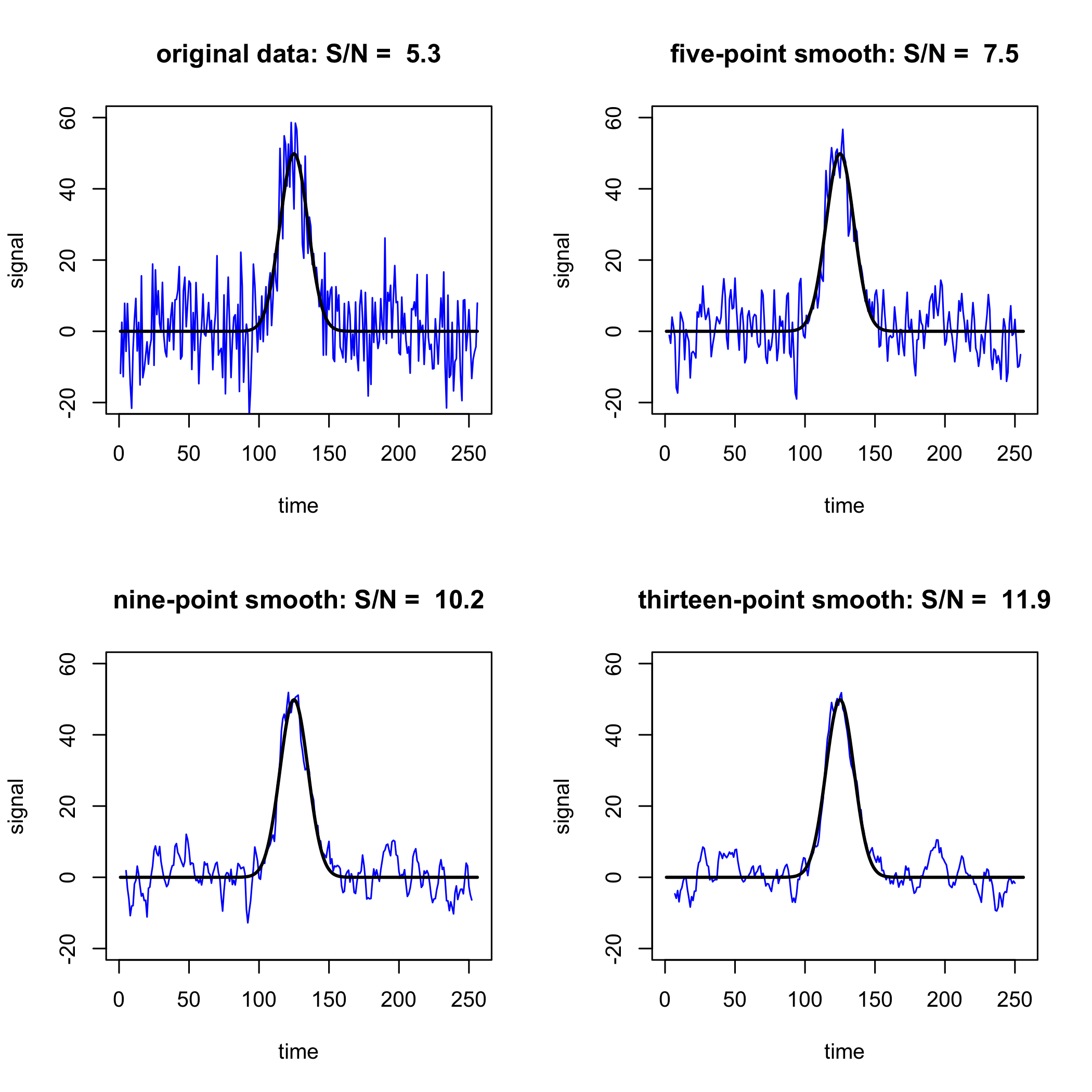
де\((S/N)_{n = 1}\) - відношення сигнал/шум для початкового сканування. Таким чином, коли\(n = 4\) відношення сигнал/шум поліпшується в 2 рази, а коли\(n = 16\) відношення сигнал/шум збільшується в 4 рази. \(\PageIndex{1}\)На малюнку показано поліпшення співвідношення сигнал/шум для сканування 1, 2, 4 та 8.
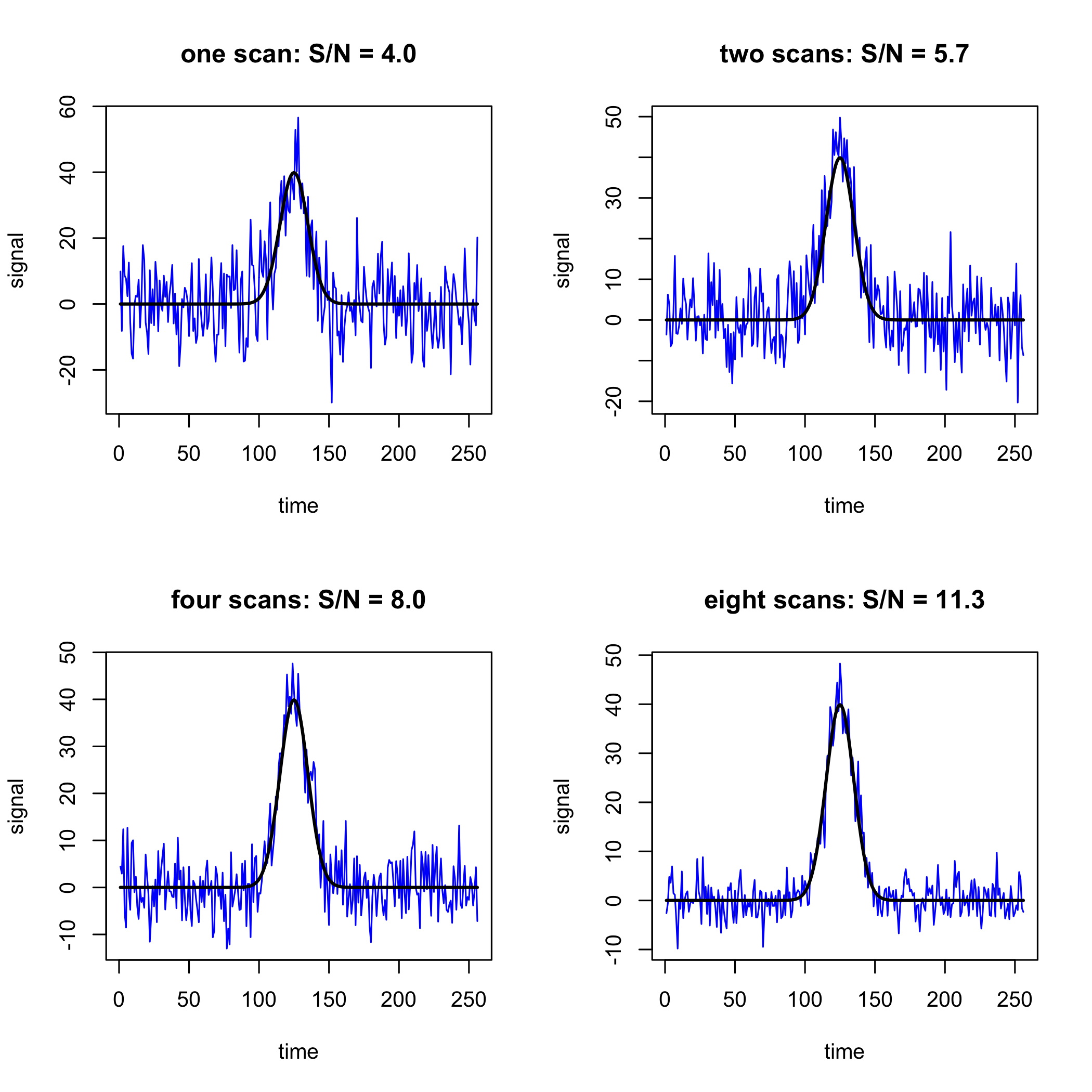
Усереднення сигналу працює добре, коли час, необхідний для збору одного сканування, короткий і коли сигнал аналіта стабільний щодо часу як тому, що зразок стабільний, так і прилад стабільний; коли це не так, то ми ризикуємо залежною від часу зміни\(S_\text{analyte}\) та/або\(s_\text{noise}\) Оскільки\((S/N)_n\) рівняння для пропорційне\(\sqrt{n}\), відносне поліпшення співвідношення сигнал/шум зменшується зі\(n\) збільшенням; наприклад, 16 сканування дає\(4 \times\) поліпшення співвідношення сигнал/шум, але це вимагає додаткових сканувань 48 (загалом 64 сканування), щоб домогтися\(8 \times\) поліпшення співвідношення сигнал/шум.
Цифрові фільтри згладжування
Однією з характеристик шуму є те, що його величина швидко коливається на відміну від основного сигналу. Ми бачимо це, наприклад, на малюнку,\(\PageIndex{1}\) де основний сигнал або залишається постійним, або постійно збільшується або зменшується, тоді як шум коливається хаотично. Цифрові фільтри згладжування скористаються цим, використовуючи математичну функцію для усереднення даних для невеликого діапазону послідовних точок даних, замінюючи середнє значення діапазону середнім сигналом у цьому діапазоні.
Фільтри ковзних середніх
Для фільтра ковзних середніх, який також називають фільтром коробки, ми замінюємо кожну точку середнім сигналом для цієї точки та рівною кількістю точок з обох боків; таким чином, фільтр ковзної середньої має ширину 3, 5, 7,... балів.\(w\) Наприклад, припустимо, що перші п'ять пунктів послідовності
| 0,80 | 0,30 | 0,80 | 0,20 | 1.00 |
то триточкове ковзне середнє (\(w = 3)\)повертає значення
| НА | 0,63 | 0,43 | 0,67 | НА |
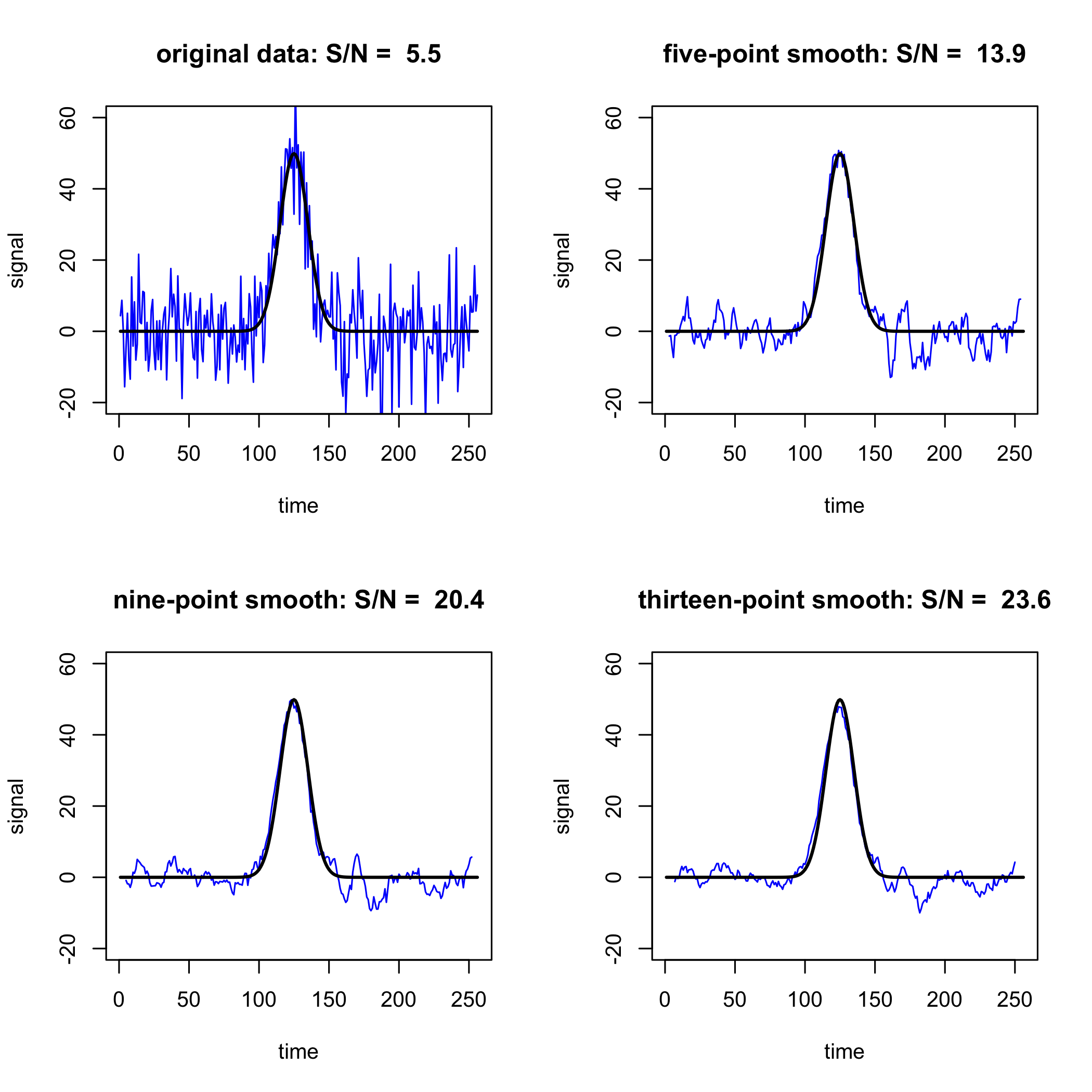
де, наприклад, 0,63 - середнє значення 0,80, 0,30 і 0,80. Зверніть увагу, що ми втрачаємо\((w - 1)/2 = (3 - 1)/2 = 1\) точки на кожному кінці набору даних, оскільки у нас немає достатньої кількості точок даних, щоб завершити розрахунок для першої та останньої точки. \(\PageIndex{2}\)На малюнку показано поліпшення\(S/N\) співвідношення при використанні фільтрів ковзної середньої шириною 5, 9 і 13.
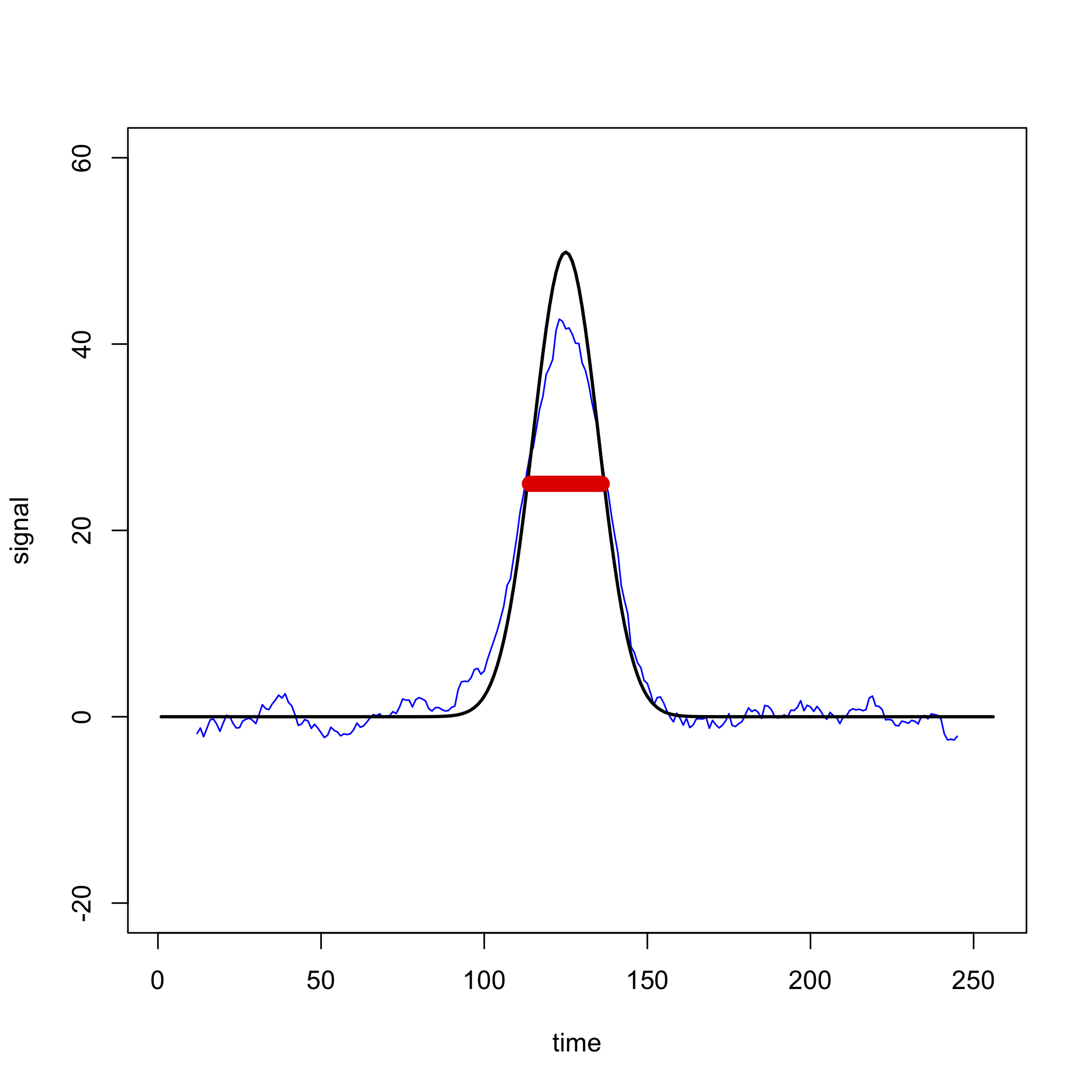
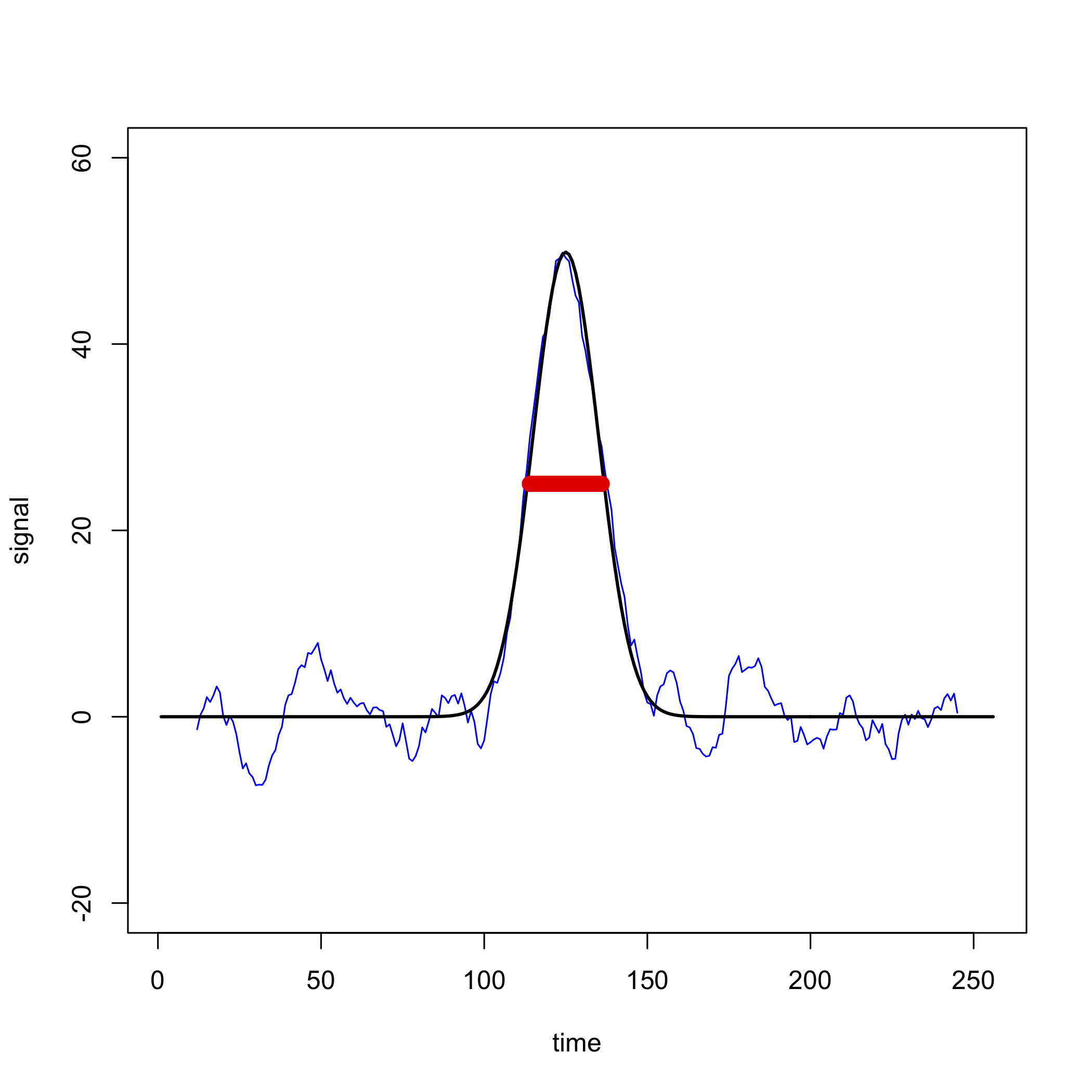
Одним з обмежень фільтра ковзних середніх є те, що він спотворює вихідні дані, видаляючи точки з обох кінців, хоча це не є серйозним занепокоєнням, якщо розглянуті точки є просто шумом. Більшу стурбованість викликає спотворення висоти сигналу, якщо ми використовуємо занадто широкий діапазон; наприклад, на малюнку\(\PageIndex{3}\) показано, як 23-бальний фільтр ковзної середньої (показаний синім кольором), застосований до шумного сигналу у верхньому лівому квадранті Рисунок\(\PageIndex{2}\), зменшує висоту вихідного сигналу (показано в чорному кольорі). Оскільки ширина фільтра, показана червоною смугою, схожа на ширину піку, оскільки фільтр проходить через пік, він систематично зменшує сигнал, усереднення разом значень, які здебільшого менші за максимальний сигнал.
Фільтри Савицьки-Голая
Фільтр ковзних середніх однаково важить усі точки; тобто точки біля країв фільтра сприяють середньому рівню рівню, рівному точкам біля центру фільтра. Фільтр Савіцкі-Голая використовує поліноміальну модель, яка зважує кожну точку по-різному, розміщуючи більшу вагу на точках поблизу центру фільтра і меншу вагу на точках біля краю фільтра. Конкретні значення залежать від розміру вікна та поліноміальної моделі; наприклад, п'ятиточковий фільтр з використанням полінома другого порядку має ваги
\[-3/35 \quad \quad 12/35 \quad \quad 17/35 \quad \quad 12/35 \quad \quad -3/35 \nonumber \]
Наприклад, припустимо, що перші п'ять пунктів послідовності
| 0,80 | 0,30 | 0,80 | 0,20 | 1.00 |
то цей фільтр Савіцкі-Голая повертає значення
| НА | НА | 0,41 | НА | НА |
де, наприклад, значення для середньої точки дорівнює
\[0.80 \times \frac{-3}{35} + 0.30 \times \frac{12}{35} + 0.80 \times \frac{17}{35} + 0.20 \times \frac{12}{35} + 1.00 \times \frac{-3}{35} = 0.406 \approx 0.41 \nonumber \]
Зверніть увагу, що ми втрачаємо\((w - 1)/2 = (5 - 1)/2 = 2\) точки на кожному кінці набору даних, де w - діапазон фільтра, тому що ми не маємо достатньої кількості точок даних для завершення обчислень. Для інших фільтрів згладжування Савицького-Голая див. Савицький, А.; Голай, М. Е., Анальний Chem, 1964, 36, 1627-1639. \(\PageIndex{4}\)На малюнку показано поліпшення\(S/N\) співвідношення при використанні фільтрів Савіцкого-Голая з використанням полінома другого порядку з 5, 9 і 13 точками.
Оскільки фільтр Savitzky-Golay важить точки інакше, ніж фільтр згладжування ковзної середньої, фільтр Савіцкі-Голая вводить менше спотворень сигналу, як ми бачимо на наступному малюнку.
Фільтрація Фур'є
Цей підхід до поліпшення співвідношення сигнал-шум використовує математичну техніку, яка називається перетворенням Фур'є (FT). Основою перетворення Фур'є є те, що ми можемо висловити сигнал у двох окремих областях. У першій області сигнал характеризується одним або декількома піками, кожен з яких визначається своїм положенням, шириною та площею; це називається частотною областю. У другій області, яка називається часовою областю, сигнал складається з набору коливань, кожен з яких визначається його частотою, амплітудою та швидкістю розпаду. Перетворення Фур'є - і зворотне перетворення Фур'є - дозволяють нам переміщатися між цими двома доменами.
Математичні деталі, що стоять за перетворенням Фур'є, виходять за рівень цього підручника; для більш глибокого розгляду зверніться до цієї серії статей з Журналу хімічної освіти:
- Гласер, Л. «Перетворення Фур'є для хіміків: частина I Вступ до перетворення Фур'є», Дж. Едук. 1987, 64, А228-А233.
- Глассер, Л. «Перетворення Фур'є для хіміків: Частина II. Перетворення Фур'є в хімії та спектроскопії», J.Chem. Едук. 1987, 64, А260—А266.
- Глассер, Л. «Перетворення Фур'є для хіміків: Частина III. Перетворення Фур'є в обробці даних», J.Chem. Едук. 1987, 64, А306-А313.
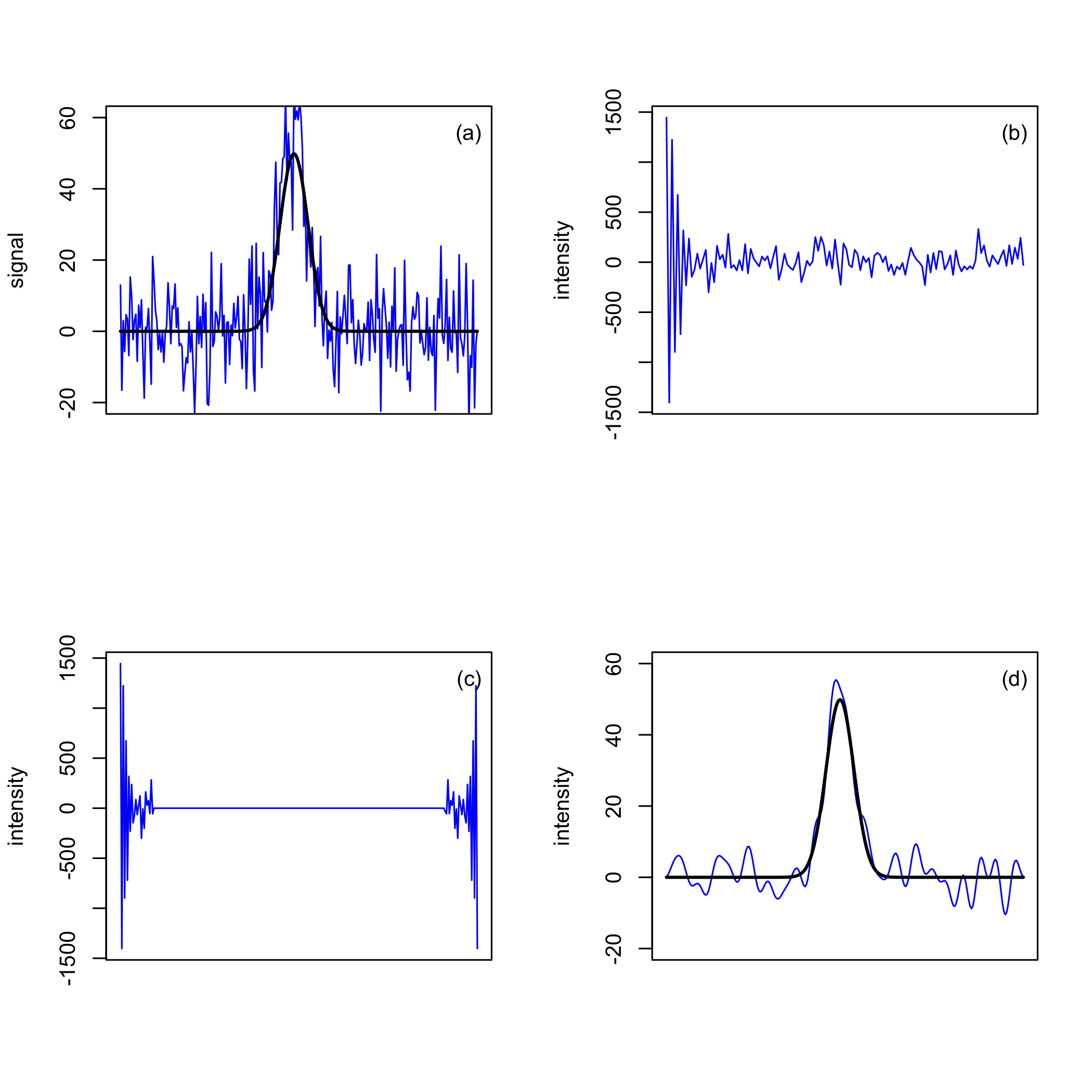
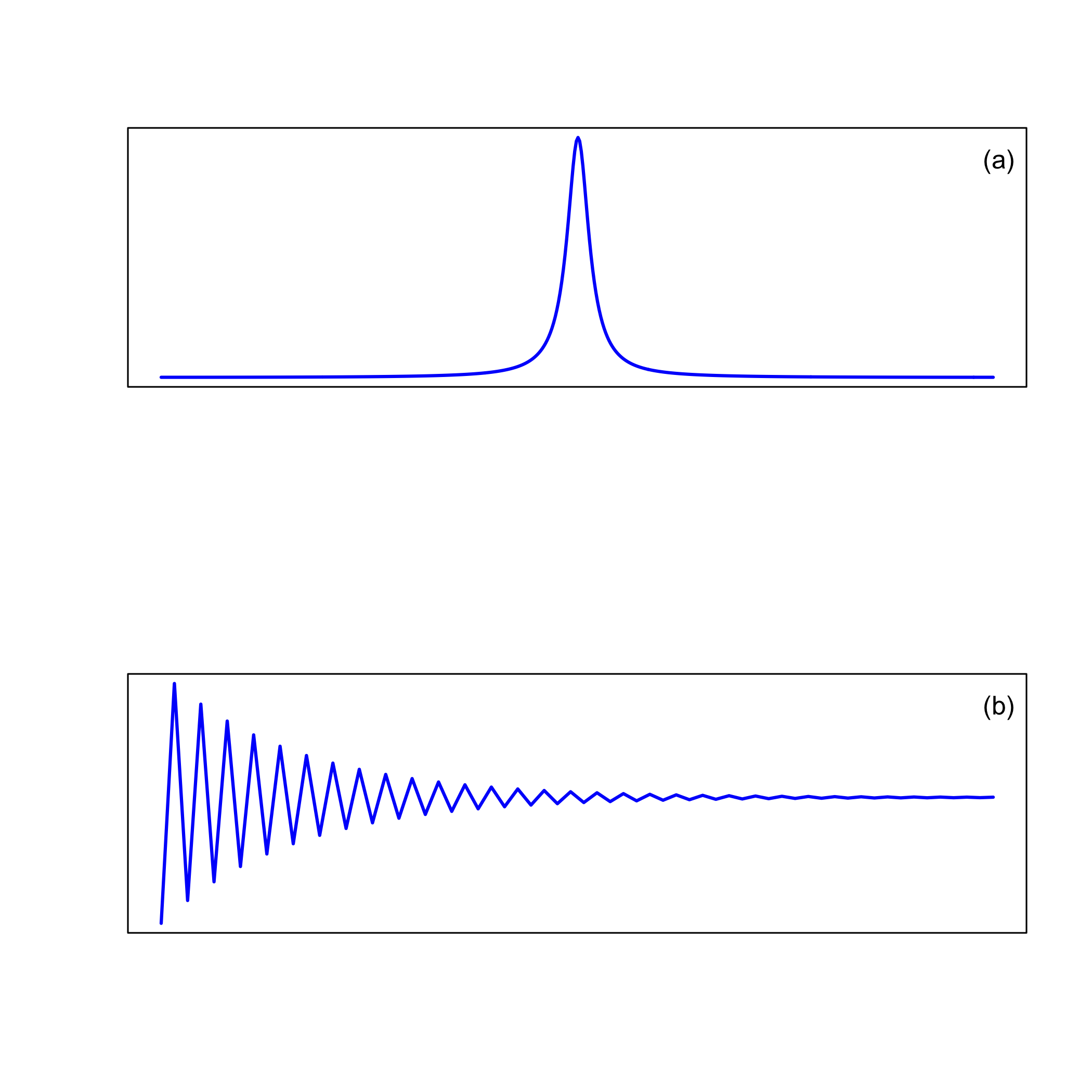
\(\PageIndex{6a}\)На малюнку показаний один пік у частотній області, а на малюнку\(\PageIndex{6b}\) показаний еквівалентний сигнал часової області. Існують кореляції між двома доменами:
- чим далі пік у частотній області знаходиться від початку, тим більша йому відповідна частота коливань у часовій області
- чим ширша ширина піку в частотній області, тим швидше швидкість його розпаду в часовій області
- чим більше площа під піком в частотній області, тим вище її початкова інтенсивність у часовій області
Ми можемо використовувати перетворення Фур'є для поліпшення співвідношення сигнал/шум, оскільки сигнал є єдиним широким піком, а шум з'являється у вигляді безлічі дуже вузьких піків. Як зазначалося вище, широкий пік у частотній області має швидкий загасаючий сигнал у часовій області, що означає, що, хоча початок сигналу часової області включає внески від сигналу та шуму, остання частина сигналу часової області включає внески лише від шуму. На малюнку нижче показано, як ми можемо скористатися цим, щоб зменшити шум та покращити співвідношення сигнал/шум для галасливого сигналу на малюнку\(\PageIndex{7a}\), який має 256 точок вздовж осі x і має відношення сигнал/шум 5.1. По-перше, ми використовуємо перетворення Фур'є для перетворення свого початкового домену в новий домен, перші 128 точок якого показані на малюнку\(\PageIndex{7b}\) (зверніть увагу: перша половина даних містить ту ж інформацію, що і друга половина даних, тому нам потрібно лише подивитися на першу половину даних). У точках на початку переважає сигнал, саме тому відбувається систематичне зниження інтенсивності коливань; в інших точках переважає шум, тому зміна інтенсивності є випадковим. Щоб відфільтрувати шум, ми зберігаємо перші 24 точки такими, якими вони є, і встановлюємо інтенсивність інших точок на нуль (вибір кількості точок для збереження може зажадати деякого коригування). Як показано на малюнку\(\PageIndex{7c}\), повторюємо це для решти 128 пунктів, зберігаючи останні 24 пункти такими, якими вони є. Нарешті, ми використовуємо зворотне перетворення Фур'є для повернення до нашої початкової області, з результатом на малюнку\(\PageIndex{7d}\), з покращенням співвідношення сигнал/шум з 5. 1 для вихідного шумового сигналу до 11,2 для відфільтрованого сигналу.