Skip to main content
LibreTexts - Ukrayinska

5.1: Співвідношення сигнал/шум

  1. Last updated
  2. Save as PDF
  • Page ID
    26927

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Коли ми робимо вимірювання, це сума двох частин, детермінантного або фіксованого внеску, що виникає з аналіту та невизначеного або випадкового внеску, який виникає внаслідок невизначеності в процесі вимірювання. Перший з них ми називаємо сигналом і називаємо останній шумом. Існує дві широкі категорії шумів: що пов'язані з отриманням зразків і пов'язані з проведенням вимірювань. Наш інтерес тут полягає в останньому.

    Що таке шум?

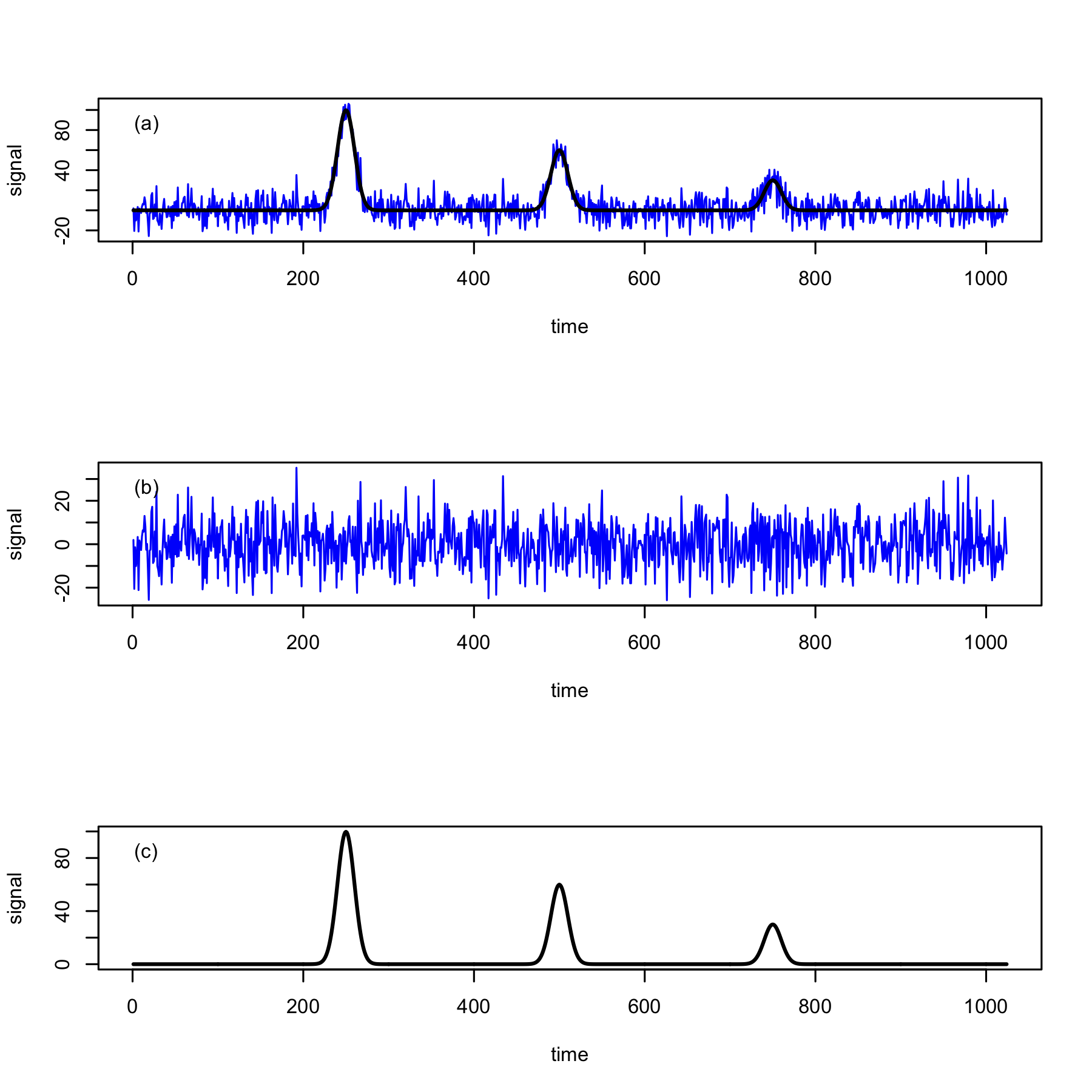
    Шум - випадкова подія, що характеризується середнім і стандартним відхиленням. Існує багато типів шуму, але ми поки обмежимося шумом, який є нерухомим, оскільки його середнє значення та його стандартне відхилення не залежать від часу, і це гетероскедастично, оскільки його середнє значення та його дисперсія (та його стандартне відхилення) не залежать від величини сигналу. \(\PageIndex{1a}\)На малюнку показаний приклад галасливого сигналу, який відповідає цим критеріям. Ось x тут показана як час - можливо хроматограма - але можливі інші одиниці, такі як довжина хвилі (спектроскопія) або потенціал (електрохімія). \(\PageIndex{1b}\)На малюнку показаний основний шум, а на малюнку\(\PageIndex{1c}\) показаний основний сигнал. Зверніть увагу, що шум на малюнку\(\PageIndex{1b}\) виглядає послідовним у своїй центральній тенденції (середньому) та його поширенні (дисперсії) вздовж осі x і не залежить від сили сигналу.

    Графіки, що показують сигнал, шум, і сигнал і шум додаються разом.
    Малюнок\(\PageIndex{1}\): Графіки, що показують (а) сигнал та шум синім кольором із сигналом, накладеного у вигляді гладкої лінії; (b) лише шум; і (c) лише сигнал. Сигнал складається з трьох піків часом 250, 500 і 750, і з максимальними значеннями 100, 60 і 30 відповідно. Шум малюється випадковим чином з нормального розподілу із середнім значенням 0 і стандартним відхиленням 10.

    Як ми характеризуємо сигнал і шум?

    Хоча ми характеризуємо шум за його середнім значенням та його стандартним відхиленням, найважливішим еталоном є відношення сигнал/шум\(S/N\), яке ми визначаємо як

    \[S/N = \frac{S_\text{analyte}}{s_\text{noise}} \nonumber \]

    де\(S_\text{analyte}\) - значення сигналу в певному місці на осі x і\(s_\text{noise}\) є стандартним відхиленням шуму з використанням частини даних без сигналу. Як загальні правила великого пальця, ми можемо виміряти сигнал з певною впевненістю, коли\(S/N \ge 3\) і ми можемо виявити сигнал з певною впевненістю, коли\(3 \ge S/N \ge 2\). Для даних на малюнку\(\PageIndex{1}\) та використання інформації в заголовку малюнка співвідношення сигнал/шум є, зліва направо, 10, 6 та 3.

    Примітка

    Для вимірювання сигналу з упевненістю означає, що ми можемо використовувати значення сигналу в розрахунку, наприклад, побудові кривої калібрування. Виявлення сигналу з упевненістю означає, що ми впевнені, що сигнал присутній (і що присутній аналіт, відповідальний за сигнал), навіть якщо ми не можемо виміряти сигнал з достатньою впевненістю, щоб забезпечити змістовний розрахунок.