1.4: Вибір аналітичного методу
- Page ID
- 26986
Аналіз зразка генерує хімічний або фізичний сигнал, пропорційний кількості аналіту в зразку. Цей сигнал може бути будь-яким, що ми можемо виміряти, такі приклади, описані в розділі 1.2. Зручно розділити аналітичні прийоми на два загальних класи виходячи з того, чи є сигнал прямо пропорційним масі або молям аналіту, або прямо пропорційний концентрації аналіта.
Розглянемо два градуйованих циліндра на малюнку\(\PageIndex{1}\), кожен з яких містить розчин 0,010 M Cu (NO 3) 2. Циліндр зліва містить 10 мл, або\(1.0 \times 10^{-4}\) молі Cu 2 +, а циліндр праворуч містить 20 мл, або\(2.0 \times 10^{-4}\) молі Cu 2 +. Якщо метод реагує на абсолютну кількість аналіту в зразку, то сигнал, обумовлений аналітом S A, подається як
\[S_A = k_A n_A \label{totalanalysis} \]
де n A - молі або грами аналіту в зразку, а k A - константа пропорційності. Оскільки циліндр праворуч містить в два рази більше молів Cu 2 +, ніж циліндр зліва, аналіз його вмісту дає сигнал вдвічі більший, ніж для іншого циліндра.

Другий клас аналітичних методів - це ті, які реагують на концентрацію аналіта, С А
\[S_A = k_A C_A \label{concanalysis} \]
При цьому аналіз вмісту двох циліндрів дає однаковий результат. Оскільки більшість інструментів реагують на концентрацію аналіта, ми обмежимося використанням Equation\ ref {concanalysis} для решти цього розділу.
Визначення проблеми
Для вибору відповідного аналітичного методу для конкретної проблеми потрібно враховувати наші потреби і порівняти їх з сильними і слабкими сторонами наявних аналітичних методів. Якщо ми відстежуємо зразки на виробничій лінії, щоб визначити, чи перевищує аналіт поріг, щоб ми могли відкласти їх для більш ретельного аналізу, то ми можемо більше розглянути швидкість, ніж точність або точність. З іншого боку, якщо наш аналіт входить до складу складної суміші, то ми, можливо, побажаємо більше розглянути аналітичні методи, що забезпечують більшу вибірковість. Або, якщо ми очікуємо, що наші зразки будуть істотно відрізнятися в концентрації аналіту, то ми можемо більше розглянути аналітичний метод, для якого Equation\ ref {concanalysis} застосовується в широкому діапазоні концентрацій.
Експлуатаційні характеристики приладів
Як було запропоновано вище, коли ми вибираємо аналітичний метод, ми узгоджуємо його експлуатаційні характеристики (або цифри заслуг) нашим потребам. Деякі з цих характеристик кількісні (точність, точність, чутливість, межа виявлення, селективність, динамічний діапазон та селективність), а інші є більш якісними (надійність, міцність, масштаб роботи, час та вартість).
Точність
Точність, або упередженість, - це міра того, наскільки близький результат експерименту до «істинного» або очікуваного результату. Ми можемо висловити точність як абсолютну похибку, е
\[e = x - \mu \nonumber \]
де\(x\) - експериментальний результат і\(\mu\) очікуваний результат, або у відсотках відносна похибка,% e r
\[\% e_r = \frac {x - \mu} {\mu} \times 100 \nonumber \]
Точність методу залежить від багатьох речей, включаючи джерело сигналу, значення k A в Equation\ ref {concanalysis} та простоту обробки зразків без втрат або забруднення.
Оскільки малоймовірно, що ми знаємо справжній результат, ми можемо використовувати очікуваний або прийнятий результат для оцінки точності. Наприклад, ми можемо використовувати стандартний довідковий матеріал, який має прийняте значення для нашого аналіта, щоб встановити точність аналітичного методу. Більш детальну обробку точності ви знайдете в Додатку 1, включаючи обговорення джерел помилок.
Точність
Коли ми аналізуємо вибірку кілька разів, індивідуальні результати варіюються від випробування до випробування. Точність - міра цієї мінливості. Чим тісніше узгодження між окремими аналізами, тим точніші результати. Наприклад, результати, наведені у верхній половині малюнка\(\PageIndex{2}\) для концентрації калію в зразку сироватки крові, більш точні, ніж результати в нижній половині малюнка\(\PageIndex{2}\). Важливо розуміти, що точність не передбачає точності. Те, що дані у верхній половині малюнка\(\PageIndex{2}\) є більш точними, не означає, що перший набір результатів є більш точним. Насправді жоден набір результатів не може бути точним.
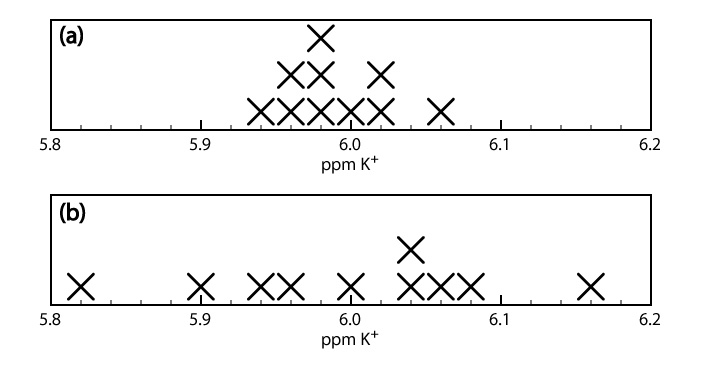
Точність методу залежить від декількох факторів, включаючи невизначеність вимірювання сигналу та простоту обробки зразків відтворюється, і повідомляється як абсолютне стандартне відхилення, с
\[s = \sqrt{\frac {\sum_{i = 1}^{n} (X_i - \overline{X})^{2}} {n - 1}} \label{sd} \]
або відносне стандартне відхилення, s r
\[s_r = \frac {s} {\overline{X}} \label{rsd} \]
де\(\overline{X}\) - середнє, або середнє значення окремих вимірів.
\[\overline{X} = \frac {\sum_{i = 1}^n X_i} {n} \label{mean} \]
Заплутана точність і точність - поширена помилка. Див. Райдер, Дж .; Кларк, А.У. Ред. 2002, 6, 1—3, і Томлінсон, Дж.; Дайсон, П.Дж .; Гарратт, Дж. Ред. 2001, 5, 16—23 для обговорення цього та інших поширених помилок щодо значення помилки. Більш детальну обробку точності ви знайдете в Додатку 1, включаючи обговорення джерел помилок.
Чутливість
Можливість продемонструвати, що два зразки мають різну кількість аналіту, є важливою частиною багатьох аналізів. Чутливість методу є мірою його здатності встановити, що така різниця є значною. Чутливість часто плутають з межею виявлення методу, яка є найменшою кількістю аналіту, який ми можемо визначити з упевненістю.
Див. Пардю, Х.Л. Клін. Хім. 1997, 43, 1831-1837 для пояснення того, чому чутливість методу не така ж, як його межа виявлення.
Чутливість еквівалентна константі пропорційності, k A, в Equation\ ref {concanalysis} [IUPAC Compendium of Chemical Terminology, Електронна версія]. Якщо\(\Delta S_A\) найменша різниця, яку ми можемо виміряти між двома сигналами, то найменша виявлена різниця в концентрації аналіта
\[\Delta C_A = \frac {\Delta S_A} {k_A} \nonumber \]
Припустимо, наприклад, що наш аналітичний сигнал - це вимір, для якого найменший виявлений приріст дорівнює ± 0,001 (довільні одиниці). Якщо чутливість нашого методу є\(0.200 \text{M}^{-1}\), то наш метод може мислимо виявити різницю в концентрації всього лише
\[\Delta C_A = \frac {\pm 0.001 } {0.200 \text{ M}^{-1}} = \pm 0.005 \text{ M}^{-1} \nonumber \]
Для двох методів з однаковим\(\Delta S_A\) методом метод з більшою чутливістю - тобто метод з більшим k A - краще може розрізняти меншу кількість аналіту.
Обмеження виявлення
Міжнародний союз чистої та прикладної хімії (IUPAC) визначає межу виявлення методу як найменшу концентрацію або абсолютну кількість аналіту, який має сигнал значно більший, ніж сигнал з відповідного бланка [IUPAC Compendium of Chemical Technology, Електронна версія]. Хоча наш інтерес полягає в кількості аналіту, в цьому розділі ми визначимо межу виявлення з точки зору сигналу аналіта. Знаючи сигнал, ми можемо обчислити концентрацію аналіта, C A, використовуючи Equation\ ref {concanalysis},\(S_A = k_A C_A\) де k - чутливість методу.
Давайте переведемо визначення межі виявлення IUPAC в математичну форму, дозволивши S mb представляти середній сигнал для порожнього методу, і дозволяючи\(\sigma_{mb}\) представляти стандартне відхилення методу бланка. Для виявлення аналіта його сигнал повинен перевищувати S mb на відповідну кількість; таким чином,
\[(S_A)_{DL} = S_{mb} \pm z \sigma_{mb} \label{detlimit} \]
\((S_A)_{DL}\)де межа виявлення аналіта.
Значення, яке ми вибираємо для z, залежить від нашого допуску для звітування про концентрацію аналіта, навіть якщо він відсутній у зразку (що називається помилкою типу 1). Зазвичай z встановлюється в три, що відповідає ймовірності\(\alpha\), 0,00135, або 0,135%. Як показано\(\PageIndex{3}\) на малюнку а, існує лише 0.135% ймовірність виявлення аналіту у зразку, який насправді не містить аналітів.
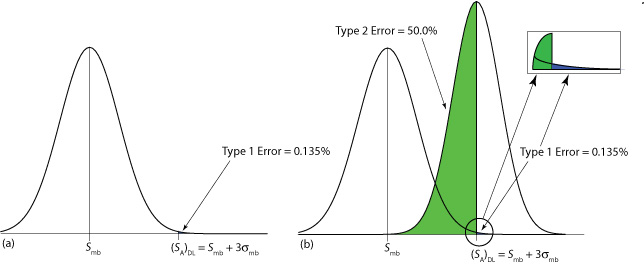
Межа виявлення також піддається помилці типу 2, в якій ми не можемо знайти докази для аналіту, навіть якщо він присутній у зразку. Розглянемо, наприклад, ситуацію, наведену на малюнку\(\PageIndex{3}\) б, де сигнал для зразка, який містить аналіт, точно дорівнює (S A) DL. У цьому випадку ймовірність помилки типу 2 становить 50%, оскільки половина можливих сигналів зразка нижче межі виявлення. Ми правильно виявляємо аналіт на межі виявлення IUPAC лише половину часу. Визначення IUPAC для межі виявлення є найменшим сигналом, для якого ми можемо сказати, на рівні значущості\(\alpha\), що аналіт присутній у зразку; однак, неможливість виявити аналіт не означає, що він відсутній у зразку.
Межа виявлення часто представляється, особливо при обговоренні питань державної політики, як окрему лінію, яка відокремлює виявлені концентрації аналітів від концентрацій, які ми не можемо виявити. Таке використання межі виявлення є неправильним [Rogers, L.B. J. Chem. Едук. 1986, 63, 3—6]. Як пропонує Рисунок\(\PageIndex{3}\), для аналіту, концентрація якого знаходиться поблизу межі виявлення, існує велика ймовірність того, що ми не зможемо виявити аналіт.
Альтернативний вираз для межі виявлення, межа ідентифікації, мінімізує помилки типу 1 і типу 2 [Long, GL; Winefordner, J.D. Anal. Хім. 1983, 55, 712—724А]. Сигнал аналіта на межі ідентифікації, (S A) LOI\(z \sigma_A\), включає додатковий термін, для обліку розподілу сигналу аналіта.
\[(S_A)_\text{LOI} = (S_A)_\text{DL} + z \sigma_A = S_{mb} + z \sigma_{mb} + z \sigma_A \label{loi} \]
Як показано на малюнку\(\PageIndex{4}\), межа ідентифікації забезпечує рівну ймовірність помилки типу 1 і 2 типу на межі виявлення. Коли концентрація аналіту знаходиться на межі ідентифікації, існує лише 0,135% ймовірність того, що його сигнал не відрізняється від сигналу методу бланка.
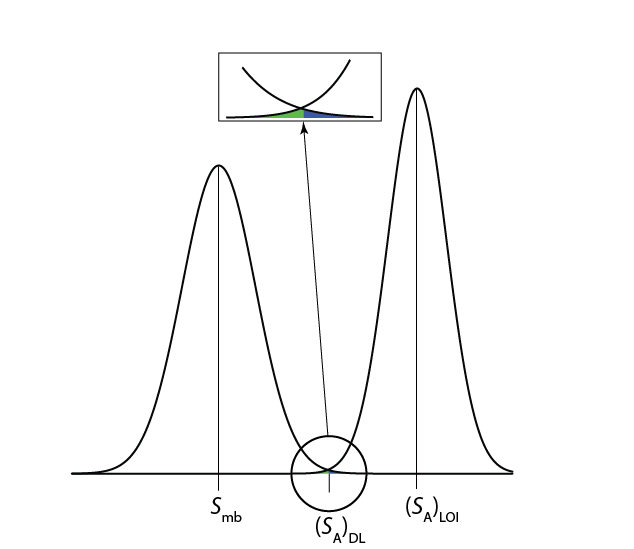
Здатність виявляти аналіт з упевненістю не те ж саме, що здатність з упевненістю повідомляти про його концентрацію, або розрізняти його концентрацію в двох зразках. З цієї причини Комітет Американського хімічного товариства з екологічної аналітичної хімії рекомендує межу кількісного визначення, (S A) LOQ [«Керівні принципи збору даних та оцінки якості даних в хімії навколишнього середовища», Анальний. Хім. 1980, 52, 2242—2249].
\[(S_A)_\text{LOQ} = S_{mb} + 10 \sigma_{mb} \label{loq} \]
Динамічний діапазон
Динамічний діапазон методу (або лінійний діапазон) проходить від межі квантування (Equation\ ref {loq}) до найвищої концентрації, для якої чутливість, k A, залишається постійною, що призводить до прямолінійного співвідношення між\(S_A\) і\(C_A\). Ця верхня межа називається межею лінійності, LOL. Між LOQ та LOL ми можемо використовувати Equation\ ref {concanalysis} для перетворення виміряного сигналу у відповідну концентрацію аналіту. Вище LOQ зв'язок між сигналом і концентрацією аналіта більше не є прямою лінією.
Вибірковість
Аналітичний метод специфічний, якщо його сигнал залежить тільки від аналіта [Перссон, Б-А; Vessman, J. Trends Anal. Хім. 1998, 17, 117-119; Перссон, Б-А; Вессман, Дж. Тренди анал. Хім. 2001, 20, 526—532]. Хоча специфіка є ідеальною, мало аналітичних методів вільні від перешкод. Коли інтерферент, I, сприяє сигналу, ми розгортаємо\ ref {totalanalysis} і Equation\ ref {concanalysis}, щоб включити його внесок у сигнал зразка, S samp
\[S_{samp} = S_A + S_I = k_A C_A + k_I C_I \label{concsamp} \]
де S I - внесок інтерферента в сигнал, k I - чутливість інтерферента, а C I - концентрація інтерферентного у зразку.
Вибірковість є мірою свободи методу від перешкод [Valca'rCel, M.; Гомес-Хенс, А.; Рубіо, С. Тренди анал. Хім. 2001, 20, 386—393]. Селективність методу для інтерференту відносно аналіту визначається коефіцієнтом селективності, K A, I
\[K_{A,I} = \frac {k_I} {k_A} \label{selectcoef} \]
які можуть бути позитивними або негативними в залежності від ознак k I і k A. Коефіцієнт селективності більше +1 або менше —1, коли метод є більш вибірковим для інтерферента, ніж для аналіту.
Хоча k A і k I зазвичай позитивні, вони можуть бути негативними. Наприклад, деякі аналітичні методи працюють шляхом вимірювання концентрації виду, який залишається після того, як він реагує з аналітом. Зі збільшенням концентрації аналіта концентрація виду, що виробляє сигнал, зменшується, а сигнал стає меншим. Якщо сигналу при відсутності аналіта присвоєно значення нуля, то наступні сигнали негативні.
Визначити значення коефіцієнта селективності легко, якщо вже відомі значення для k A і k I. Як показано на прикладі\(\PageIndex{1}\), ми також можемо визначити K A, I шляхом вимірювання S samp при наявності та за відсутності інтерферента.
Спосіб аналізу Ca 2+ у воді страждає від перешкод у присутності Zn 2 +. Коли концентрація Са 2 + в 100 разів більше, ніж Zn 2 +, аналіз на Ca 2 + має відносну похибку +0,5%. Який коефіцієнт вибірковості для цього методу?
Рішення
Оскільки повідомляється лише відносні концентрації, ми можемо довільно призначити абсолютні концентрації. Щоб зробити розрахунки легкими, дозволимо C Ca = 100 (довільні одиниці) і C Zn = 1. Відносна похибка +0,5% означає, що сигнал при наявності Zn 2 + на 0,5% більше сигналу при відсутності Zn 2 +. Знову ж таки, ми можемо призначити значення, щоб полегшити розрахунок. Якщо сигнал для Cu 2 + при відсутності Zn 2 + дорівнює 100 (довільні одиниці), то сигнал при наявності Zn 2 + дорівнює 100,5.
Значення k Ca визначається за допомогою рівняння\ ref {concanalysis}
\[k_\text{Ca} = \frac {S_\text{Ca}} {C_\text{Ca}} = \frac {100} {100} = 1 \nonumber \]
При наявності Zn 2 + сигнал подається рівнянням\ ref {concsamp}; таким чином
\[S_{samp} = 100.5 = k_\text{Ca} C_\text{Ca} + k_\text{Zn} C_\text{Zn} = (1 \times 100) + k_\text{Zn} \times 1 \nonumber \]
Розв'язування для k Zn дає його значення як 0,5. Коефіцієнт вибірковості дорівнює
\[K_\text{Ca,Zn} = \frac {k_\text{Zn}} {k_\text{Ca}} = \frac {0.5} {1} = 0.5 \nonumber \]
Якщо ви не впевнені, чому в наведеному вище прикладі сигнал в присутності цинку дорівнює 100,5, зверніть увагу, що процентна відносна похибка для цієї проблеми задається
\[\frac {\text{obtained result} - 100} {100} \times 100 = +0.5 \% \nonumber \]
Розв'язування дає отриманий результат 100,5.
Коефіцієнт селективності надає нам корисний спосіб оцінити потенційний вплив інтерферента на аналіз. Розв'язування рівняння\ ref {selectcoef} для k I
\[k_I = K_{A,I} \times k_A \label{ki} \]
і підставляючи в рівняння\ ref {concanalysis} і спрощення дає
\[S_{samp} = k_A \{ C_A + K_{A,I} \times C_I \} \label{S_samp} \]
Інтерферент не створюватиме проблеми, якщо термін\(K_{A,I} \times C_I\) у Equation\ ref {S_SAMP} значно менший за C A.
Барнетт і його колеги розробили метод визначення концентрації кодеїну (структура показана нижче) в рослині маку [Barnett, N.W.; Bowser, T. A.; Geraldi, RD; Smith, B Anal. Чим. Акт 1996, 318, 309— 317]. В рамках свого дослідження вони оцінювали ефект декількох втручань. Наприклад, автори виявили, що еквимолярні розчини кодеїну і інтерферентного 6-метоксикодеїну подають сигнали відповідно 40 і 6 (довільні одиниці).
(а) Який коефіцієнт селективності для інтерферентного, 6-метоксикодеїну, відносно того, що для аналіту, кодеїну.
(б) Якщо нам потрібно знати концентрацію кодеїну з точністю ± 0,50%, яка максимальна відносна концентрація 6-метокси-кодеїну, яку ми можемо переносити?
Рішення
(а) Сигнали, зумовлені аналітом, S A, і інтерферент, S I, є
\[S_A = k_A C_A \quad \quad S_I = k_I C_I \nonumber \]
Розв'язування цих рівнянь для k A та k I та підставляючи їх до рівняння\ ref {selectcoef} дає
\[K_{A,I} = \frac {S_I / C_I} {S_A / C_I} \nonumber \]
Оскільки концентрації аналіту та інтерферентного є рівномолярними (C A = C I), коефіцієнт селективності дорівнює
\[K_{A,I} = \frac {S_I} {S_A} = \frac {6} {40} = 0.15 \nonumber \]
(б) Для досягнення точності кращої ± 0,50% термін\(K_{A,I} \times C_I\) у рівнянні\ ref {S_SAMP} повинен бути менше 0,50% від C A; таким чином
\[K_{A,I} \times C_I \le 0.0050 \times C_A \nonumber \]
Розв'язуючи цю нерівність для співвідношення C I/C A і підставляючи в значення K A, I з частини (a) дає
\[\frac {C_I} {C_A} \le \frac {0.0050} {K_{A,I}} = \frac {0.0050} {0.15} = 0.033 \nonumber \]
Тому концентрація 6-метоксикодеїну повинна бути менше 3,3% від концентрації кодеїну.
Проблеми з вибірковістю також більш імовірні, коли аналіт присутній в дуже низькій концентрації [Роджерс, Л.Б. Едук. 1986, 63, 3—6].
Міцність і міцність
Щоб метод був корисним, він повинен забезпечити достовірні результати. На жаль, методи піддаються різним хімічним і фізичним втручанням, які сприяють невизначеності аналізу. Якщо метод відносно вільний від хімічних перешкод, ми можемо використовувати його для аналізу аналіту в широкому спектрі матриць зразків. Такі методи вважаються робастними.
Випадкові варіації експериментальних умов вносять невизначеність. Якщо чутливість методу, k, занадто залежить від експериментальних умов, таких як температура, кислотність або час реакції, то незначна зміна будь-якого з цих умов може дати значно інший результат. Міцний метод відносно нечутливий до змін експериментальних умов.
Масштаб операції
Іншим способом звузити вибір методів є врахування трьох потенційних обмежень: кількість зразка, доступного для аналізу, очікувана концентрація аналіту в зразках і мінімальна кількість аналіту, який буде виробляти вимірюваний сигнал. У сукупності ці обмеження визначають масштаб операцій аналітичного методу.
Ми можемо відобразити масштаб операцій візуально (Рисунок\(\PageIndex{5}\)) шляхом побудови розміру зразка на осі x і концентрацію аналіта на осі y. Для зручності ми ділимо зразки на макро (>0,1 г), мезо (10 мг—100 мг), мікро (0,1 мг—10 мг) та ультрамікро (<0.1 mg) sizes, and we divide analytes into major (> 1% ж/б), незначні (0,01% w/w— 1% w/w), слідові (10 —7% w/w— 0,01% w/w) та ультра-слідові (<10 —7% w/w) компоненти. Разом концентрація аналіта та розмір зразка забезпечують характерний опис для аналізу. Наприклад, в мікрослідовому аналізі зразок важить від 0,1 мг до 10 мг і містить концентрацію аналіту між 10 -7% w/w і 10 —2% w/w.
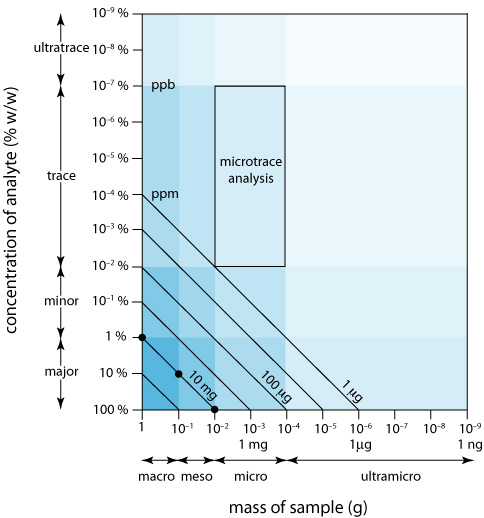
Діагональні лінії, що з'єднують осі, показують комбінації розміру зразка та концентрації аналіту, які містять однакову абсолютну масу аналіту. Як показано на малюнку\(\PageIndex{5}\), наприклад, 1-г зразок, який становить 1% w/w аналіт, має таку ж кількість аналіту (10 мг), що і 100-мг зразка, що становить 10% w/w аналіт, або 10-мг зразок, який є 100% w/w аналіт.
Ми можемо використовувати Figure\(\PageIndex{5}\) для встановлення обмежень для аналітичних методів. Якщо мінімальний виявлений сигнал методу еквівалентний 10 мг аналіту, то він найкраще підходить для основного аналіту в макро- або мезозразку. Подовження методу на аналіт з концентрацією 0,1% ж/б вимагає проби 10 г, що рідко буває практичним через ускладнення перенесення такої великої кількості матеріалу через аналіз. З іншого боку, невеликий зразок, який містить слідову кількість аналіту, встановлює значні обмеження на аналіз. Наприклад, 1-мг зразок, який становить 10 -4% w/w в аналіті містить лише 1 нг аналіту. Якщо виділити аналіт в 1 мл розчину, то нам потрібен аналітичний метод, який достовірно зможе виявити його в концентрації 1 нг/мл.
Обладнання, час та вартість
Нарешті, ми можемо порівняти аналітичні методи щодо їх потреб у обладнанні, часу, необхідного для проведення аналізу, та вартості зразка. Методи, які покладаються на приладобудування, є інтенсивними і можуть вимагати значної підготовки операторів. Наприклад, графітова піч атомно-абсорбційної спектроскопічний метод визначення свинцю у воді вимагає значних капітальних вкладень в прилад і досвідченого оператора для отримання достовірних результатів. Інші методи, такі як титриметрія, вимагають менш дорогого обладнання та меншої підготовки.
Час для завершення аналізу для одного зразка часто досить схожий від методу до методу. Однак це дещо вводить в оману, оскільки значна частина цього часу витрачається на підготовку зразків, підготовку реагентів та збір обладнання. Після того, як зразки, реагенти та обладнання будуть встановлені, частота дискретизації може істотно відрізнятися. Наприклад, для аналізу одного зразка свинцю за допомогою графітової печі атомно-абсорбційної спектроскопії потрібно всього кілька хвилин, але кілька годин для аналізу того ж зразка за допомогою гравіметрії. Це суттєвий фактор при виборі методу для лабораторії, яка обробляє великий обсяг зразків.
Вартість аналізу залежить від багатьох факторів, включаючи вартість обладнання та реактивів, вартість найму аналітиків, кількість зразків, які можна обробити за годину. Загалом, методи, які покладаються на інструменти, коштують дорожче за зразок, ніж інші методи.
Робимо остаточний вибір
На жаль, критерії проектування, розглянуті в цьому розділі, не є взаємно незалежними [Valca'rCel, M.; RiOs, A.Anal. Хім. 1993, 65, 781—787А]. Робота з меншими зразками або поліпшення селективності часто відбувається за рахунок точності. Мінімізація витрат і часу аналізу може знизити точність. Вибір методу вимагає ретельного балансування різних критеріїв проектування. Зазвичай найважливішим критерієм проектування є точність, а найкращим методом вважається той, який дає максимально точний результат. Коли потреба в результаті є нагальною, як це часто буває в клінічних лабораторіях, час аналізу може стати критичним фактором.
У деяких випадках саме властивості зразка визначають найкращий метод. Наприклад, зразок зі складною матрицею може зажадати методу з відмінною селективністю, щоб уникнути перешкод. Зразки, в яких аналіт присутній в слідовій або ультраслідовій концентрації, зазвичай вимагають методу концентрації. Якщо кількість зразка обмежена, то метод не повинен вимагати великої кількості проби.
