CO-4: Розрізняють різні шкали вимірювань, вибирають відповідні описові та інференційні статистичні методи на основі цих відмінностей та інтерпретують результати.
Цілі навчання
LO 4.20: Класифікуйте ситуацію аналізу даних за участю двох змінних відповідно до «класифікації рольового типу».
Цілі навчання
LO 4.35: Для ситуації аналізу даних, що включає дві змінні, виберіть відповідний метод виводу для вивчення зв'язку між змінними та обґрунтуйте вибір.
Цілі навчання
LO 4.36: Для ситуації аналізу даних, що включає дві змінні, виконайте відповідний метод висновків для вивчення зв'язків між змінними та зробіть правильні висновки в контексті.
У попередній одиниці ми навчилися виконувати висновок для однієї категоріальної або кількісної змінної у вигляді точкової оцінки, довірчих інтервалів або тестування гіпотез.
Висновок був насправді
- про частку населення (коли змінна інтересів була категоричною) і
- про середнє значення популяції (коли змінна інтерес була кількісною).
Наша наступна (і кінцева) мета цього курсу полягає в тому, щоб виконати висновок про відносини між двома змінними в популяції, на основі спостережуваного співвідношення між змінними у вибірці. Ось як виглядає процес:
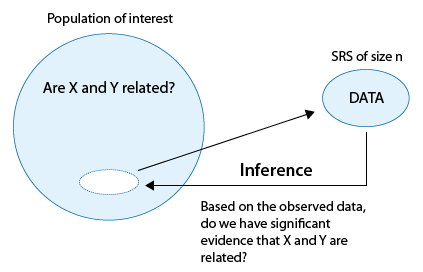
Ми зацікавлені у вивченні того, чи існує зв'язок між змінними X і Y в цікавить популяції. Вибираємо випадкову вибірку і збираємо дані по обох змінних з суб'єктів.
Наша мета полягає в тому, щоб визначити, чи дають ці дані достатньо вагомі докази для нас, щоб узагальнити спостережуваний зв'язок у вибірці та зробити висновок (з деяким прийнятним та узгодженим рівнем невизначеності), що відносини між X і Y існує у всій популяції.
Основною формою висновку, яку ми будемо використовувати в цій одиниці, є тестування гіпотез, але ми обговоримо довірчі інтервали як для оцінки невідомих параметрів, що цікавлять, за участю двох змінних, так і як альтернативний спосіб визначення висновку до нашої гіпотези. тест.
Концептуально, для всіх методів виводу, які ми дізнаємося, ми перевіримо деяку форму:
Ho: Немає зв'язку між X і Y
Ха: Існує зв'язок між X і Y
(Ми також обговоримо точкову та інтервальну оцінку, але наша дискусія про ці форми висновку буде оформлена навколо тесту.)
Нагадаємо, що коли ми обговорювали вивчення взаємозв'язку між двома змінними в блоці Exploratory Data Analysis, наша дискусія була обговорена навколо класифікації рольового типу. Ця частина курсу буде структурована точно так само.
Іншими словами, ми розглянемо тестування гіпотез у розділах 3, що відповідають випадкам C→Q, C→C та Q→Q у таблиці нижче.
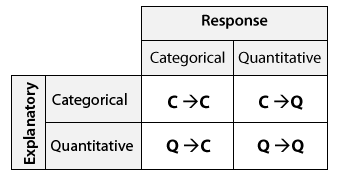
Нагадаємо, що випадок Q→C не розглядається спеціально в цьому курсі, крім того, що ми можемо досліджувати зв'язок між цими змінними за допомогою тих самих методів, що і випадок C→Q.
Важливо також пам'ятати, що ми дізналися про приховані змінні та причинно-наслідкові зв'язки.
- Якщо наша пояснювальна змінна була частиною добре розробленого експерименту, то ми можемо претендувати на причинний ефект.
- Але якщо він базувався на спостережному дослідженні, ми повинні бути обережними, маючи на увазі лише зв'язок або асоціацію між двома змінними, а не прямий причинно-наслідковий зв'язок між пояснювальна та змінна відповіді.
На відміну від попередньої частини курсу з умовиводу для однієї змінної, де ми детально розглянули теорію, що стоїть за машиною тесту (наприклад, нульовий розподіл тестової статистики, під якою обчислюються p-значення), у процедурах виводу, які ми введемо в умовивід для Відносини, ми будемо обговорювати набагато менше такого роду деталей.
Принципи ті ж, але деталі, що стоять за нульовим розподілом тестової статистики (за якою обчислюється p-значення) ускладнюються і вимагають знання теоретичних результатів, які виходять за рамки цього курсу.
Замість цього в межах кожного з методів виводу ми зосередимося на:
- Коли інференційний метод доречний до використання.
- За яких умов процедуру можна сміливо використовувати.
- Концептуальна ідея, що стоїть за тестом (як це зазвичай захоплюється статистикою тесту).
- Як використовувати програмне забезпечення для проведення процедури, щоб отримати p-значення тесту.
- Інтерпретація результатів в контексті проблеми.
- Також ми продовжимо вводити кожен тест відповідно до чотириетапного процесу тестування гіпотез.
Двосторонні тести
З цього моменту ми, як правило, зосередимося на
- ДВОСТОРОННІ тести і
- Доповнюйте довірчими інтервалами для ефекту інтересу, щоб дати додаткову інформацію
Використання двосторонніх тестів є стандартною практикою в клінічних дослідженнях НАВІТЬ тоді, коли існує напрямок інтересу для гіпотези дослідження, наприклад, бажання довести нове лікування краще, ніж поточне лікування.
Ось кілька коментарів:
Тепер ми готові розпочати роботу з Case C→Q.

