CO-6: Застосовуйте основні поняття ймовірності, випадкових варіацій та зазвичай використовуваних статистичних розподілів ймовірностей.
ПРИМІТКА: У наступних відео обговорюються всі три сторінки, пов'язані з розподілом вибірки.
Рецензія: Ми будемо застосовувати поняття нормальних випадкових величин до двох випадкових величин, які є зведеною статистикою з вибірки — це середнє значення вибірки (x-bar) та пропорція вибірки (p-hat).
Вступ
Вже неодноразово ми вказували на важливу відмінність між населенням та вибіркою. У дослідницькому аналізі даних ми навчилися підсумувати та відображати значення змінної для зразка, наприклад, відображення груп крові 100 випадково обраних дорослих США за допомогою кругової діаграми, або відображення висот 150 чоловіків за допомогою гістограми та доповнення її відповідним числовим такі заходи, як середнє значення зразка (x-bar) та стандартне відхилення (и) зразка.
У нашому дослідженні ймовірності та випадкових величин ми обговорювали довгострокову поведінку змінної, враховуючи популяцію всіх можливих значень, прийнятих цією змінною. Наприклад, ми говорили про розподіл груп крові серед усіх дорослих людей США і розподілі випадкової величини X, що представляє зростання чоловіка.
Тепер зупинимося безпосередньо на зв'язку між значеннями змінної для вибірки і її значеннями для всієї сукупності, з якої була взята вибірка. Цей матеріал є мостом між ймовірністю і нашою кінцевою метою курсу, статистичним висновком. У висновку дивимося на зразок і запитуємо, що можна сказати про населення, з якого він був зроблений.
Тепер ми поставимо зворотне питання: якщо я знаю, як виглядає популяція, як я можу очікувати, як виглядатиме зразок? Зрозуміло, що висновок ставить більш практичне питання, оскільки на практиці ми можемо подивитися на зразок, але рідко ми знаємо, як виглядає вся популяція. Цей матеріал матиме більш теоретичний характер, оскільки створює проблему, яка насправді не є практичною, але представить важливі ідеї, які є основою для статистичного висновку.
Параметри проти статистики
Цілі навчання
LO 6.19: Визначте та розрізняйте параметр та статистику.
Цілі навчання
LO 6.20: Поясніть поняття мінливості вибірки та розподілу вибірки.
Щоб краще зрозуміти взаємозв'язок між вибіркою і сукупністю, розглянемо два приклади, які були згадані у вступі.
ПРИКЛАД 1: Група крові - варіативність відбору проб
У розділі ймовірності ми представили розподіл груп крові по всьому населенню США:
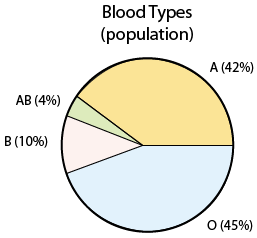
Припустімо тепер, коли ми беремо вибірку з 500 людей у Сполучених Штатах, записуємо їх групу крові та відобразили результати вибірки:
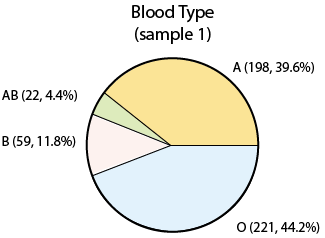
Зверніть увагу, що відсотки (або пропорції), які ми знайшли в нашій вибірці, трохи відрізняються від відсотків населення. Це дійсно не дивно. Оскільки ми взяли вибірку всього 500, ми не можемо очікувати, що наша вибірка буде вести себе так само, як населення, але якщо вибірка випадкова (як це було), ми очікуємо отримати результати, які знаходяться не так далеко від населення (як ми це робили). Якщо ми взяли ще один зразок розміром 500:
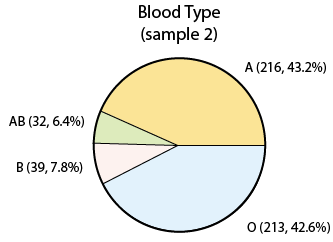
ми знову отримуємо вибіркові результати, які трохи відрізняються від чисельності населення, а також відрізняються від того, що ми знайшли в першій вибірці. Ця дуже інтуїтивна ідея, що результати вибірки змінюються від зразка до зразка, називається варіативністю вибірки.
Давайте розглянемо інший приклад:
Приклад 2: Висота дорослих чоловіків - варіативність відбору проб
Висоти серед популяції всіх дорослих самців слідують за нормальним розподілом із середнім μ = мю = 69 дюймів і стандартним відхиленням σ = сигма = 2,8 дюйма. Ось вірогідність відображення цього розподілу населення:
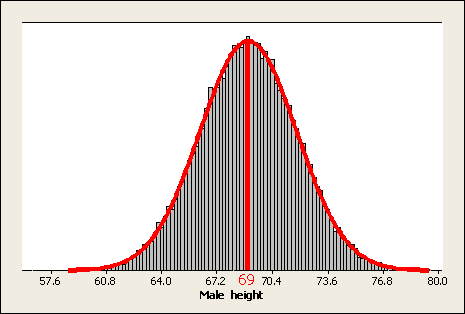
Була обрана вибірка з 200 самців, і зафіксовані їх висоти. Ось зразки результатів:
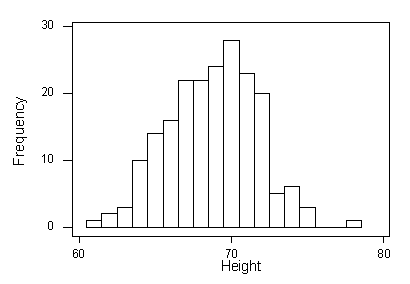
Середнє значення зразка (x-bar) становить 68,7 дюйма, а стандартне відхилення (и) зразка - 2,95 дюйма.
Знову ж таки, зверніть увагу, що результати вибірки трохи відрізняються від популяції. Гістограма для цього зразка нагадує нормальний розподіл, але не настільки тонка, а також середнє значення вибірки і стандартне відхилення дещо відрізняються від середнього значення популяції та стандартного відхилення. Візьмемо ще один зразок з 200 самців:
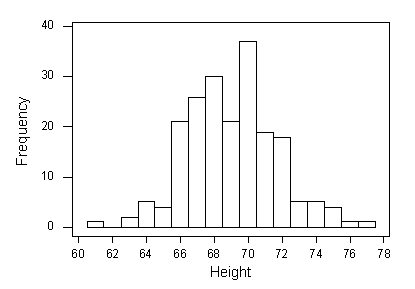
Середнє значення зразка (x-bar) становить 69,1 дюйма, а стандартне відхилення (и) зразка - 2,66 дюйма.
Знову ж таки, як у прикладі 1 ми бачимо ідею варіативності вибірки. У цій другій вибірці результати досить близькі до популяції, але відрізняються від результатів, які ми знайшли в першій вибірці.
В обох прикладах ми маємо числа, які описують сукупність, і цифри, які описують вибірку. У прикладі 1 число 42% - це частка населення групи крові А, а 39,6% - частка вибірки (у зразку 1) групи крові А. У прикладі 2, 69 та 2,8 - середнє та стандартне відхилення населення, а (у вибірці 1) 68,7 та 2,95 - середнє та стандартне відхилення вибірки.
Параметр - це число, яке описує сукупність.
Статистика - це число, яке обчислюється з вибірки.
ПРИКЛАД 3: Параметри проти статистики з прикладів 1 і 2
У прикладі 1:42% (0,42) - параметр і 39,6% (0,396) - статистика (а 43,2% - інша статистика).
У прикладі 2:69 і 2.8 - параметри, а 68.7 і 2.95 - статистика (69.1 і 2.66 також статистика).
У цьому курсі, як і в прикладах вище, ми орієнтуємося на наступні параметри і статистику:
- Частка населення та частка вибірки
- середнє значення населення та середнє вибіркове
- стандартне відхилення населення та стандартне відхилення вибірки
Наступна таблиця підсумовує три пари і дає позначення
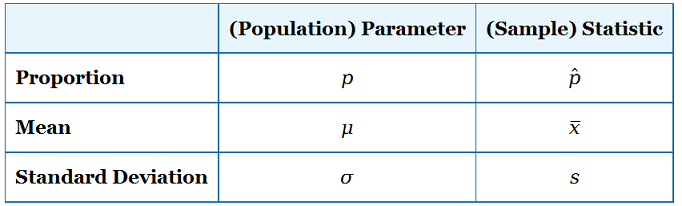
Єдиним новим позначенням тут є p для пропорції населення (p = 0,42 для типу A у прикладі 1) та p-hat (використовуючи символ «капелюх» над p) для пропорції вибірки, яка становить 0,396 у прикладі 1, зразок 1).
Коментарі:
- Параметри, як правило, невідомі, оскільки недоцільно або неможливо точно знати, які значення приймає змінна для кожного члена популяції.
- Статистика обчислюється з вибірки і варіюється від вибірки до вибірки через мінливість вибірки.
В останній частині курсу, статистичний висновок, ми навчимося використовувати статистику, щоб зробити висновки про невідомий параметр, або оцінюючи його, або вирішивши, чи доцільно зробити висновок, що параметр дорівнює запропонованому значенню.
Тепер ми дізнаємося про поведінку статистики, припускаючи, що ми знаємо параметри. Так, наприклад, якщо ми знаємо, що частка населення групи крові А в популяції становить 0,42, і ми беремо випадкову вибірку розміром 500, що ми очікуємо, що пропорція вибірки p-hat буде? Зокрема ми запитуємо:
- Який розподіл всіх можливих пропорцій вибірки зі зразків розміром 500?
- Де вона зосереджена?
- Скільки варіацій існує серед різних пропорцій зразків із зразків розміром 500?
- Наскільки далеко від справжнього значення 0,42 ми можемо очікувати?
Ось ще кілька прикладів:
ПРИКЛАД 4: Параметри проти статистики
Якщо студенти вибирали числа абсолютно випадковим чином з чисел від 1 до 20, частка разів, що число 7 буде вибрано, становить 0,05. Коли 15 студентів вибрали число «навмання» від 1 до 20, 3 з них вибрали число 7. Визначте параметр і супутню статистику в даній ситуації.
Параметр - це частка населення випадкових виборів, що призводять до числа 7, що дорівнює p = 0,05. Супровідна статистика - це пропорція вибірки (p-hat) виділень, що призводить до числа 7, що становить 3/15 = 0,20.
Примітка: Не пов'язане з нашою поточною дискусією, це цікава ілюстрація того, як ми (люди) не дуже добре робимо речі випадковим чином. Раніше я задавав подібне питання на вступних курсах статистики, де я просив студентів ВИПАДКОВО вибрати число між 1 і 10. Кількість студентів, які обирають 7, майже завжди НАБАГАТО більше, ніж було б передбачено, якби результати були справді випадковими.
Спробуйте з деякими своїми друзями та родиною і подивіться, чи отримаєте ви подібні результати. Нам дуже подобається число 7! Цікаво, що якщо студенти були в курсі цього явища, то вони, як правило, вибирали 3 найчастіше. Це цікаво, оскільки якщо вибір був справді випадковим, ми повинні побачити відносно рівну частку для кожного числа :-)
ПРИКЛАД 5: Параметри проти статистики
Тривалість вагітності людини має середнє значення 266 днів і стандартне відхилення в 16 днів. Випадкова вибірка з 9 вагітних жінок мала середню тривалість вагітності 270 днів зі стандартним відхиленням 14 днів. Визначте параметри і супровідну статистику в даній ситуації.
Параметрами є середнє значення населення μ = mu =266 і стандартне відхилення населення σ = сигма = 16. Супровідною статистикою є середнє значення вибірки (x-bar) = 270 і стандартне відхилення вибірки (s) = 14.
Першим кроком до висновків про параметри на основі супровідної статистики є розуміння того, як поводяться вибіркові статистичні дані щодо параметра (ів), який узагальнює всю сукупність. Почнемо з поведінки пропорції вибірки щодо частки населення (коли змінна, що цікавить, категорична). Після цього ми вивчимо поведінку середнього зразка щодо середнього популяції (коли змінна, що цікавить, кількісна).






