СО-1: Опишіть ролі, яку виконує біостатистика в дисципліні охорони здоров'я.
CO-6: Застосовуйте основні поняття ймовірності, випадкових варіацій та зазвичай використовуваних статистичних розподілів ймовірностей.
Огляд великої картини
Цілі навчання
LO 1.3: Визначте та розмежуйте компоненти загальної картини статистики
Нагадаємо, Велика картина — чотириетапний процес, який охоплює статистику (як вона представлена в цьому курсі):
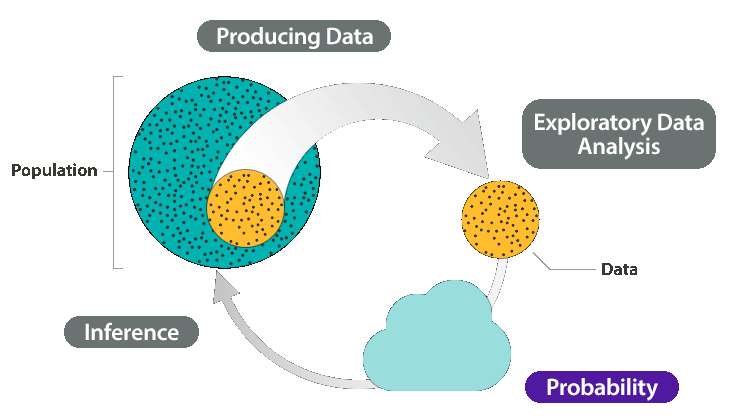
Поки що ми обговорили перші два кроки:
Виробництво даних — як отримані дані та які міркування впливають на процес виробництва даних.
Дослідницький аналіз даних - інструменти, які допомагають нам спочатку відчути дані, розкриваючи їх особливості за допомогою візуальних дисплеїв та числових резюме, які допомагають нам досліджувати розподіли, порівнювати розподіли та досліджувати зв'язки.
(Нагадаємо, що структура цього курсу така, що спочатку було висвітлено дослідницький аналіз даних, а потім - виробництво даних.)
Нашою кінцевою метою є висновок - зробити достовірні висновки про населення на основі того, що ми виявили в нашій вибірці.
Для того, щоб дійсно зрозуміти, як працює висновок, ми спочатку повинні поговорити про ймовірність, тому що це основа для методів статистичного висновку.
Одиниця ймовірності починається з введення, яке дасть вам кілька мотивуючих прикладів та інтуїтивний та неформальний погляд на ймовірність.
Навіщо нам розуміти ймовірність?
- Ми часто хочемо оцінити ймовірність того, що подія (цікавить нас) відбудеться.
- Багато цінностей, що представляють інтерес, є ймовірностями або походять від ймовірностей, наприклад, рівня поширеності, рівня захворюваності та чутливість/специфічності тестів на захворювання.
- Плюс!! Інференційна статистика спирається на ймовірність
- Тестові гіпотези
- Оцініть значення населення, такі як середнє значення населення або частка населення.
Ймовірність і умовивід
Ми використаємо приклад, щоб спробувати пояснити, чому ймовірність настільки важлива для висновку.
По-перше, ось загальна ідея:
Як ми всі знаємо, спосіб роботи статистики полягає в тому, що ми використовуємо вибірку, щоб дізнатися про населення, з якого вона була зроблена. В ідеалі вибірка повинна бути випадковою, щоб вона добре представляла населення.
Нагадаємо, з дискусії про вибірку, що коли ми говоримо, що випадкова вибірка добре представляє популяцію, ми маємо на увазі, що в цій техніці вибірки немає властивого упередженості.
Однак важливо визнати, що це не означає, що всі випадкові зразки обов'язково «ідеальні». Випадкові зразки все ще є випадковими, і тому жодна випадкова вибірка не буде точно такою ж, як інша.
Одна випадкова вибірка може дати досить точне уявлення про населення, тоді як інша випадкова вибірка може бути «вимкнена», чисто через випадковість.
На жаль, розглядаючи ту чи іншу вибірку (що і відбувається на практиці), ми ніколи не дізнаємося, наскільки він відрізняється від популяції.
Ця невизначеність - це те, де ймовірність приходить в картину. Це дає нам можливість зробити висновки про популяції в умовах невизначеності, яка породжується використанням випадкової вибірки.
Ми використовуємо ймовірність кількісної оцінки того, наскільки ми очікуємо, що випадкові зразки змінюватимуться.
Наступний приклад проілюструє цей важливий момент.
ПРИКЛАД:
Припустимо, що ми зацікавлені в оцінці відсотка дорослих США, які виступають за смертну кару.
Для цього ми обираємо випадкову вибірку з 1200 дорослих США та запитуємо їхню думку: або на користь, або проти смертної кари.
Ми виявляємо, що 744 з 1200, або 62%, виступають за. (Коментар: хоча це лише приклад, ця цифра в 62% цілком реалістична, враховуючи деякі останні опитування).
Ось картина, яка ілюструє те, що ми зробили і знайшли в нашому прикладі:
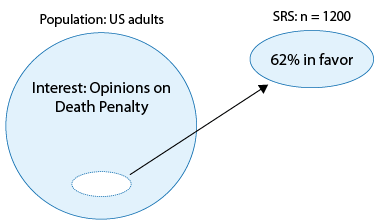
Нашою метою тут є висновок — дізнатися і зробити висновки про думки всього населення США дорослих щодо смертної кари, виходячи з думок лише 1200 з них.
Чи можемо ми зробити висновок, що 62% населення виступає за смертну кару?
- Інший випадковий зразок міг дати зовсім інший результат. Тож ми невпевнені.
Але оскільки наша вибірка випадкова, ми знаємо, що наша невизначеність обумовлена випадковістю, а не через проблеми з тим, як був зібраний зразок.
Таким чином, ми можемо використовувати ймовірність опису ймовірності того, що наш зразок знаходиться в межах бажаного рівня точності.
Наприклад, ймовірність може відповісти на питання: «Наскільки ймовірно, що наша вибіркова оцінка становить не більше 3% від справжнього відсотка всіх дорослих США, які виступають за смертну кару?»
Відповідь на це питання (яке ми знаходимо з використанням ймовірності), очевидно, матиме важливий вплив на впевненість, яку ми можемо прикріпити до кроку висновку.
Зокрема, якщо ми вважаємо досить малоймовірним, що відсоток вибірки буде сильно відрізнятися від відсотка населення, то у нас є велика впевненість, що ми можемо зробити висновки про чисельність населення на основі вибірки.
У науках про здоров'я порівнянна ситуація із прикладом смертної кари буде, коли ми хочемо визначити поширеність певного захворювання чи стану.
В епідеміології поширеність стану, пов'язаного зі здоров'ям (типово захворювання, але також інших речей, таких як куріння або використання ременів безпеки) у статистичній популяції визначається як загальна кількість випадків у популяції, розділена на кількість осіб у популяції.
Як ми побачимо, це форма ймовірності.
На практиці нам потрібно буде оцінити поширеність за допомогою вибірки і для того, щоб зробити висновки про популяції з вибірки, нам потрібно буде зрозуміти ймовірність.
ПРИКЛАД:
CDC підрахував, що в 2011 році 8,3% населення США хворіють на діабет. Іншими словами, CDC оцінює поширеність діабету в 8,3% в США.
Є численні статистичні дані та графіки, повідомлені в цьому документі, ви повинні тепер зрозуміти!!
Інші поширені ймовірності, що використовуються в науках про здоров'я, є
- (Накопичувальна) Захворюваність: ймовірність того, що людина, яка не має попереднього захворювання, розвине захворювання протягом певного певного періоду часу
- Чутливість діагностичного або скринінгового тесту: ймовірність того, що людина отримує позитивний результат, враховуючи, що людина має захворювання. Специфіка діагностичного або скринінгового тесту: ймовірність того, що людина тестує негативно, враховуючи, що людина не має захворювання. А також прогнозне значення позитивне, прогнозне значення негативне, хибнопозитивний показник, помилково негативний показник.
- Імовірність виживання: ймовірність того, що індивід виживає понад певний час

