причинно-наслідковий зв'язок

Last updated
Save as PDF

Page ID: 99550

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

СО-1: Опишіть ролі, яку виконує біостатистика в дисципліні охорони здоров'я.

Відео

Відео: Причинність (8:45)

Вступ

Цілі навчання

LO 1.6: Визнайте різницю між асоціацією та причинно-наслідковою причиною.

Цілі навчання

LO 1.7: Визначте потенційні змінні, що ховаються для пояснення спостережуваних відносин.

Поки ми обговорювали різні способи, за допомогою яких дані можуть бути використані для вивчення зв'язку (або асоціації) між двома змінними. Для нашого обговорення ми слідували таблиці класифікації рольового типу:

Будь-який тип пояснювальної змінної можна поєднати з будь-яким типом змінної відповіді. Можливими сполученнями є: Категорична пояснювальна → Категорична відповідь (C → C), Категорична пояснювальна → Кількісна відповідь (C → Q), кількісна пояснювальна → Категорична відповідь (Q → C) та кількісна пояснювальна → Кількісна відповідь (Q → Q).

Зараз ми завершили навчання, як досліджувати відносини у випадках C → Q, C → C та Q→Q (Як зазначалося раніше, випадок Q→C не обговорюватиметься в цьому курсі.)

Коли ми досліджуємо зв'язок між двома змінними, часто виникає спокуса зробити висновок із спостережуваного співвідношення, що зміни в пояснювальній змінній викликають зміни змінної відповіді. Іншими словами, у вас може виникнути спокуса інтерпретувати спостережувану асоціацію як причинно-наслідковий зв'язок.

Мета цієї частини курсу полягає в тому, щоб переконати вас, що такого роду інтерпретація часто є неправильною! Девіз цього розділу - один з найбільш фундаментальних принципів цього курсу:

СЛОВА, ЩОБ ЖИТИ: Статистичний аналіз поодинці ніколи не доведе причинно-наслідковий зв'язок!

ПРИНЦИП: Асоціація не передбачає причинно-наслідкового зв'язку!

Зовнішнє читання: Причина та наслідки (≈ 1700 слів)

Почнемо з наступного прикладу:

ПРИКЛАД: Пошкодження вогнем

Графік розсіювання нижче ілюструє, як кількість пожежників, відправлених на пожежі (X), пов'язана з величиною збитків, заподіяних пожежами (Y) у певному місті.

Розсіювач, в якому горизонтальна вісь позначена «# Пожежників», а вертикальна вісь позначена «Пошкодження ($)». Вертикальна вісь коливається від 0 до $2500000, а горизонтальна вісь коливається від 0 до 40.

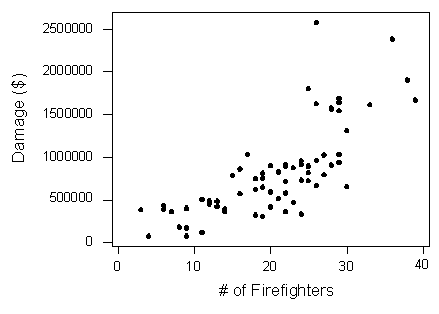
Розсіювач чітко відображає досить сильну (злегка вигнуту) позитивну залежність між двома змінними. Чи було б тоді розумним зробити висновок, що відправка більшої кількості пожежників на пожежу завдає більшої шкоди, або що місто повинно направляти менше пожежників на пожежу, щоб зменшити кількість збитків, завданих пожежею? Звичайно, ні! Так що ж тут відбувається?

На задньому плані є третя змінна - серйозність пожежі - яка відповідає за спостережувані відносини. Більш серйозні пожежі вимагають більшої кількості пожежників, а також завдають більшої шкоди.

Наступний малюнок допоможе вам наочно уявити цю ситуацію:

Блок-схема. «Серйозність вогню» - це «прихована змінна». Це є причиною як «Кількість пожежників (X)», так і «сума збитку (Y)» Ми помилково спостерігали «спостережувану асоціацію» між «Кількість пожежників (X)" та «Сума збитку (Y)»

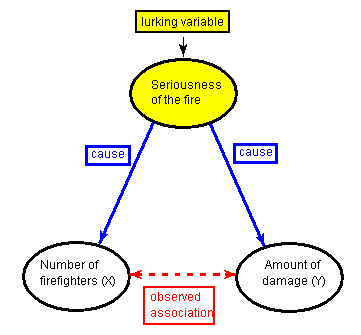
Тут серйозність пожежі - таїться змінна. Змінна, що ховається - це змінна, яка не входить до числа пояснювальних або змінних відповіді в дослідженні, але може суттєво вплинути на вашу інтерпретацію відносин між цими змінними.

Тут ми маємо наступні три відносини:

Шкода збільшується з кількістю пожежників
Кількість пожежників збільшується з гостротою пожежі
Збиток збільшується з тяжкістю пожежі
При цьому збільшення збитку з числом пожежників може частково або повністю пояснюватися тяжкістю пожежі.

Зокрема, як і в нашому прикладі, змінна, що ховається, може впливати як на пояснювальну, так і на змінну відповіді. Цей загальний ефект створює спостережувану асоціацію між пояснювальними та змінними відповіді, хоча між ними немає причинно-наслідкового зв'язку. Ця можливість, що може бути прихована змінна (про яку ми можемо не думати), яка відповідає за спостережувані відносини, призводить до нашого принципу:

ПРИНЦИП: Асоціація не передбачає причинно-наслідкового зв'язку!

Наступний приклад проілюструє інший спосіб, яким прихована змінна може втручатися і перешкоджати нам досягти будь-яких причинно-наслідкових висновків.

ПРИКЛАД: Тест SAT

Для американських коледжів та університетів стандартним вступним іспитом є тест SAT. Пліч-о-пліч boxplots нижче дають докази зв'язку між країною походження студента (США або іншою країною) та балом SAT Math студента.

Пліч-о-пліч поле сюжет. Вертикальна вісь має маркування «SAT Math Score», і вона коливається від 450 до 800. Горизонтальна вісь має маркування «Країна» і має дві категорії: «Інше» і «США».

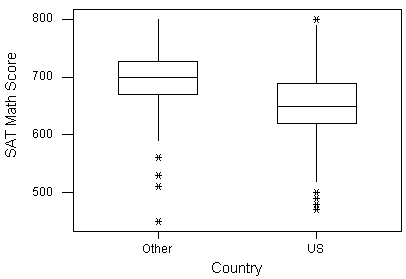
Розподіл балів іноземних студентів вище, ніж у американських студентів. Середній бал іноземних студентів (близько 700) перевищує третій квартиль балів студентів США. Чи можемо ми зробити висновок, що країна походження є причиною різниці в балах SAT Math, і що студенти в Сполучених Штатах слабкіші в математиці, ніж студенти в інших країнах?

Ні, не обов'язково. Хоча це може бути правдою, що американські студенти відрізняються математичними здібностями від інших студентів - тобто через відмінності в освітніх системах - ми не можемо зробити висновок, що країна походження студента є причиною нерівності. Однією з важливих прихованих змінних, яка може пояснити спостережуваний зв'язок, є освітній рівень двох груп населення, які приймають тест SAT Math. У Сполучених Штатах SAT є стандартним тестом, і тому широкий перетин всіх студентів США (з точки зору освітнього рівня) проходять цей тест. Серед усіх іноземних студентів, з іншого боку, тест здають лише ті, хто планує приїхати до США на навчання, яка, як правило, є більш вибраною підгрупою.

Наведений нижче малюнок допоможе вам наочно уявити це пояснення:

Блок-схема. У нас є дві причини, одна з яких - «Рівень освіти SAT Takers». Це «Прихована змінна" Інша причина - «Національність (X)». Обидва вони можуть бути причинами «SAT-математичного балу (Y)». Ми спостерігали зв'язок між «Національність (X)» та «SAT-Math Score (Y)». Зверніть увагу, що між цими двома змінними також є підозрювана причина зв'язку.

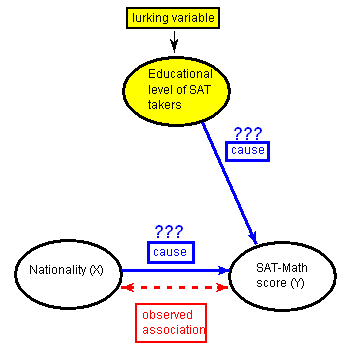
Тут пояснювальна змінна (X) може мати причинно-наслідковий зв'язок із змінною відповіді (Y), але змінна, що ховається, також може бути фактором, що сприяє, що робить його дуже важко ізолювати ефект пояснювальної змінної та довести, що вона має причинно-наслідковий зв'язок зі змінною відповіді . У цьому випадку ми говоримо, що прихована змінна плутається з пояснювальною змінною, оскільки їх вплив на змінну відповіді неможливо відрізнити один від одного.

Зауважимо, що в кожному з вищевказаних двох прикладів змінна, що ховається, по-різному взаємодіє з досліджуваними змінними. У прикладі 1 змінна, що ховається, впливає як на пояснювальну, так і на змінну відповіді, створюючи ілюзію того, що між ними існує причинно-наслідковий зв'язок. У другому прикладі змінна, що ховається, плутається з пояснювальною змінною, що ускладнює оцінку ізольованого впливу пояснювальної змінної на змінну відповіді.

Різниця між цими двома типами взаємодій не настільки важлива, як той факт, що в будь-якому випадку спостережувана асоціація може бути хоча б частково пояснена прихованою змінною. Отже, найважливішим повідомленням з цих двох прикладів є: Спостережувана асоціація між двома змінними не є достатнім доказом того, що між ними існує причинно-наслідковий зв'язок.

Іншими словами...

ПРИНЦИП: Асоціація не передбачає причинно-наслідкового зв'язку!

Навчіться, роблячи: причинно-наслідковий зв'язок

Парадокс Сімпсона

Цілі навчання

LO 1.8: Визнайте та поясніть явище парадоксу Сімпсона, оскільки воно стосується інтерпретації взаємозв'язку між двома змінними.

Поки що у нас є:

обговорювали, що ховаються змінні,
продемонстрували різні способи, за допомогою яких приховані змінні можуть взаємодіяти з двома досліджуваними змінними, і
зрозумів, що існування можливої прихованої змінної є основною причиною, чому ми говоримо, що асоціація не передбачає причинно-наслідкового зв'язку.

Як ви пам'ятаєте, прихована змінна, за визначенням, є змінною, яка не була включена в дослідження, але може мати істотний вплив на наше розуміння взаємозв'язку між двома досліджуваними змінними.

Що робити, якщо ми включили приховану змінну в наше дослідження? Який вплив це може мати на наше розуміння відносин? Це питання, які ми збираємося обговорити далі.

Почнемо з прикладу:

ПРИКЛАД: Показники смертності в лікарнях

Довідкова інформація: Урядове дослідження зібрало дані про рівень смертності майже в 6000 лікарнях США. Потім ці результати були оскаржені дослідниками, які заявили, що федеральні аналізи не враховували різницю між лікарнями щодо тяжкості захворювань пацієнтів, коли вони були госпіталізовані. В результаті, за словами дослідників, деякі лікарні ставилися несправедливо у висновках, які назвали лікарні з більш високим, ніж очікувалося, рівнем смертності. Дослідники мали на увазі, що коли федеральний уряд досліджував взаємозв'язок між двома змінними - лікарнею та смертністю - він також повинен був включити в дослідження (або врахувати) приховану змінну - тяжкість хвороби.

Ми будемо використовувати спрощену версію цього дослідження, щоб проілюструвати твердження дослідників, і подивитися, який можливий ефект може бути від включення прихованої змінної в дослідження. (Довідка: Мур і Маккейб (2003). Вступ до практики статистики.)

Розглянемо наступну двосторонню таблицю, в якій узагальнені дані про стан пацієнтів, які були госпіталізовані в дві лікарні певного міста (лікарня А і лікарня Б). Зауважте, що оскільки метою дослідження є вивчення того, чи існує «лікарняний ефект» на статус пацієнтів, «Лікарня є пояснювальною змінною, а «Статус пацієнта» - змінною відповіді.

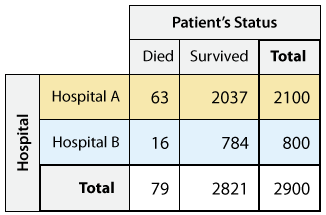
Коли ми доповнимо двосторонню таблицю умовними відсотками всередині кожної лікарні:

Двостороння таблиця з тими ж рядками та стовпцями, що і попередня двостороння таблиця, за винятком рядка Всього було вилучено. Ось дані в тому ж форматі: Лікарня А, Помер: 3%; Лікарня А, Вижив: 97%; Лікарня А, Всього: 100%; Лікарня B, Помер: 2%; Лікарня B, Вижив: 98%; Лікарня B, Всього: 100%;

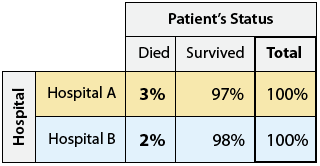
ми виявляємо, що лікарня А має вищий рівень смертності (3%), ніж лікарня B (2%). Чи варто стрибати до висновку, що хворий пацієнт, який потрапив до лікарні А, на 50% частіше помирає, ніж якби він/вона була госпіталізована до лікарні В? Не так швидко...

Можливо, лікарня А отримує більшість важких випадків, і це пояснює, чому вона має вищий рівень смертності. Для того, щоб дослідити це, нам потрібно включити (або врахувати) приховану змінну «тяжкість хвороби» в наш аналіз. Для цього ми повертаємося до двостороннього столу і розділимо його, щоб окремо подивитися на пацієнтів, які важко хворіють, і пацієнтів, які не є.

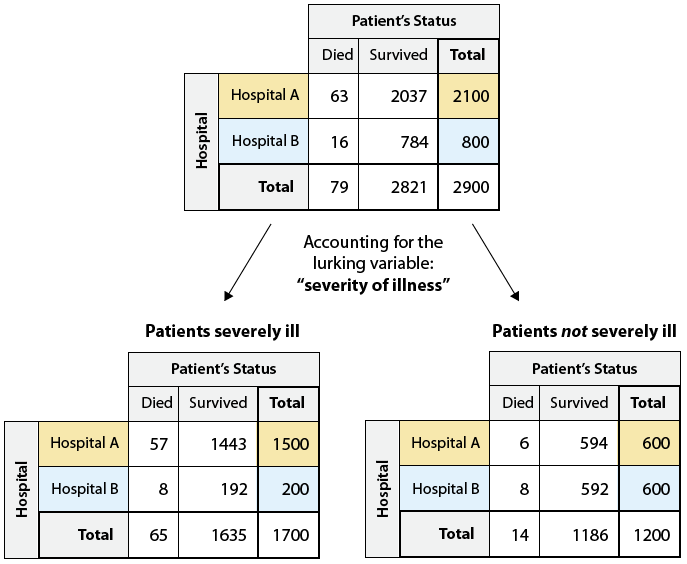
Як ми бачимо, лікарня А прийняла набагато важкохворих пацієнтів, ніж лікарня B (1500 проти 200). Насправді, з того, як були розділені підсумки, ми бачимо, що в лікарні А важкохворих пацієнтів становили набагато більшу частку пацієнтів - 1500 із загальної кількості 2100 пацієнтів. На відміну від цього, лише 200 з 800 пацієнтів лікарні В були тяжко хворі. Щоб краще побачити ефект включення прихованої змінної, нам потрібно доповнити кожну з двох нових двосторонніх таблиць її умовними відсотками:

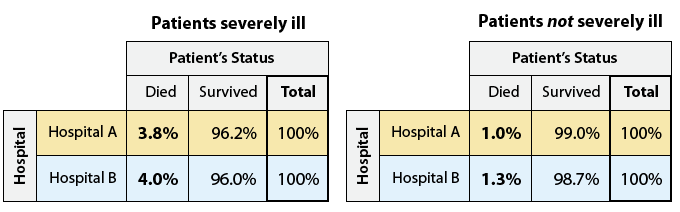
Зауважте, що незважаючи на наше попереднє виявлення того, що загальна лікарня А має вищий рівень смертності (3% проти 2%), коли ми враховуємо приховану змінну, ми виявляємо, що насправді саме лікарня B має вищий рівень смертності як серед важкохворих пацієнтів (4% проти 3,8%), так і серед не тяжкохворих пацієнтів (1,3% проти 1%). Таким чином, ми бачимо, що додавання прихованої змінної може змінити напрямок асоціації.

Тут ми маємо наступні три відносини:

Більший відсоток пацієнтів лікарні А помер порівняно з лікарнею Б.
Важко хворі пацієнти рідше виживають.
Лікарня А приймає більш важкохворих пацієнтів.
У цьому випадку, після подальшого ретельного аналізу, ми бачимо, що як тільки ми враховуємо тяжкість хвороби, лікарня А насправді має менший відсоток пацієнтів, які померли, ніж лікарня В в обох групах пацієнтів!

Всякий раз, коли включення прихованої змінної змушує нас переосмислити напрямок асоціації, це називається парадокс Сімпсона.

Можливість того, що прихована змінна може мати такий драматичний ефект, є ще однією причиною, чому ми повинні дотримуватися принципу:

ПРИНЦИП: Асоціація не передбачає причинно-наслідкового зв'язку!

Заключний приклад - отримання глибшого розуміння відносин

Не завжди так, що включення прихованої змінної змушує нас переосмислити напрямок асоціації. У наступному прикладі ми побачимо, як включення прихованої змінної просто допомагає нам глибше зрозуміти спостережувані відносини.

ПРИКЛАД: вступні іспити до коледжу

Як обговорювалося раніше, в Сполучених Штатах SAT - це широко використовуваний вступний іспит до коледжу, необхідний найпрестижнішим школам. У деяких штатах, інший вступний іспит коледжу є поширеним, ACT.

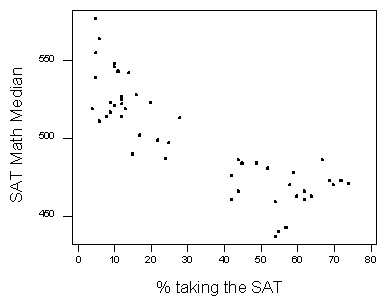
Зверніть увагу, що:

пояснювальна змінна - відсоток, що приймає SAT,
змінна відповіді - це медіана оцінка SAT Math, і
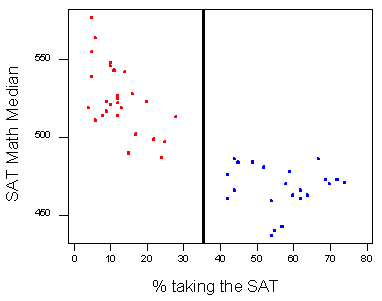
кожна точка даних на розсіювальному графіку представляє один із штатів, так, наприклад, в штаті Іллінойс, за рік ці дані були зібрані, 16% студентів взяли SAT Math, а їх середній бал становив 528.

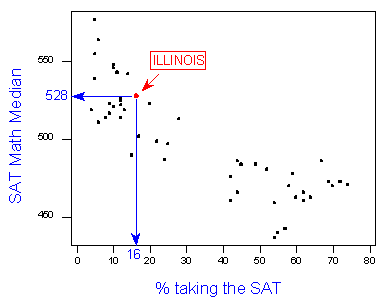
Зверніть увагу, що існує негативний зв'язок між відсотком студентів, які приймають SAT в державі, і середнім балом SAT Math в цьому стані. Яким може бути пояснення цієї негативної тенденції? Чому може мати більше людей пройти тест бути пов'язаний з більш низькими балами?

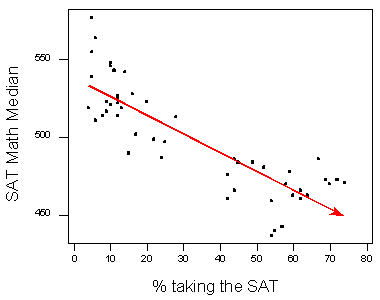
Зверніть увагу, що ще однією видимою особливістю даних є наявність зазору посередині розсіювача, який створює два різних кластера в даних. Це говорить про те, що, можливо, існує прихована змінна, яка розділяє стани на ці два кластери, і що включення цієї прихованої змінної в дослідженні (як ми це робили, створюючи цей мічений scatterplot) допоможе нам зрозуміти негативну тенденцію.

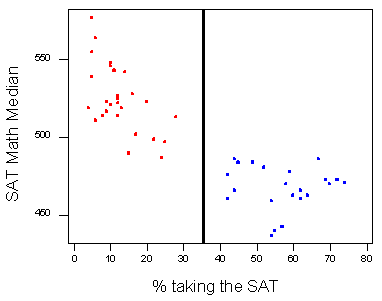
Виявляється, дійсно, кластери представляють дві групи станів:

«Синя група» праворуч представляє держави, де SAT є випробуванням на вибір для студентів та коледжів.
«Червона група» зліва представляє держави, де зазвичай використовується вступний іспит до коледжу ACT.

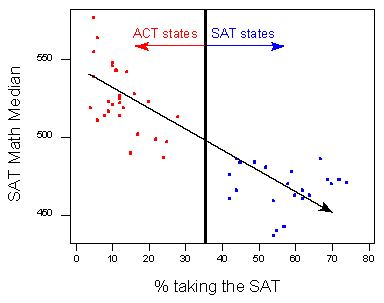
Має сенс тоді, що в «ACT держави» зліва, менший відсоток студентів беруть SAT. Більше того, студенти, які приймають SAT в штатах ACT, ймовірно, студенти, які звертаються до більш престижних національних коледжів, і тому представляють більш вибрану групу студентів. Це причина, чому ми бачимо високі бали SAT Math в цій групі.

З іншого боку, у «SAT штатах» праворуч більший відсоток студентів здають тест. Ці студенти представляють набагато ширший переріз населення, і тому ми бачимо нижчі (більш середні) бали SAT Math.

Підводячи підсумок: У цьому випадку включення прихованої змінної «стан ACT» проти «SAT state» допомогло нам краще зрозуміти спостережуваний негативний зв'язок у наших даних.

Навчіться, роблячи: причинно-наслідкові зв'язки та приховані змінні

Чи я отримав це? : Парадокс Сімпсона

Останні два приклади показали нам, що включення прихованої змінної в нашу розвідку може:

змусити нас переосмислити напрямок асоціації (як у прикладі лікарня/смертності) або,
допоможіть нам глибше зрозуміти взаємозв'язок між змінними (як у прикладі SAT/ACT).

Підіб'ємо підсумки

Змінна, що ховається - це змінна, яка не була включена до вашого аналізу, але яка може суттєво змінити вашу інтерпретацію даних, якщо вони були включені.

Через можливість приховування змінних ми дотримуємося принципу, що асоціація не передбачає причинно-наслідкового зв'язку.

Включення прихованої змінної в нашу розвідку може:
- допомогти нам глибше зрозуміти взаємозв'язок між змінними, або
- змусити нас переосмислити напрямок асоціації (Парадокс Сімпсона)

Всякий раз, коли включення прихованої змінної змушує нас переосмислити напрямок асоціації, це приклад парадоксу Сімпсона.