Середина

Last updated
Save as PDF

Page ID: 97316

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Результати навчання

Знайдіть середину між двома числами.
Намалюйте середину двох чисел на числовій лінії.

Як звучить слово, «середина» означає «точка посередині». Знайти середину не надто складно і має застосування в багатьох областях статистики, від довірчих інтервалів до ескізів розподілів, до засобів.

Пошук середньої точки між двома числами

Якщо нам дано два числа, то середина - це лише середнє значення двох чисел. Щоб обчислити середину, складаємо їх і потім ділимо результат на 2. Формула виглядає наступним чином:

Визначення: середина

\(a\)\(b\)Дозволяти і бути два числа. Тоді середина,\(M\) з цих двох чисел

\[M\:=\frac{a+b}{2} \label{midpoint}\]

Приклад\(\PageIndex{1}\)

Знайти середину чисел\(3.5\) і\(7.2\).

Рішення

Найголовніше в пошуку середньої точки полягає в тому, що додавання двох чисел повинно відбуватися до ділення на 2. Ми можемо або зробити це один крок за раз в нашому калькуляторі, або ми можемо вкласти суму в дужки. У цьому прикладі ми спочатку виконаємо додавання:

\[3.5+7.2\:=\:10.7 \nonumber\]

Тепер ми готові розділити на 2:

\[\frac{10.7}{2}=5.35 \nonumber\]

Таким чином, середина 3,5 і 7,2 дорівнює 5,35.

Приклад\(\PageIndex{2}\)

Основною темою в статистиці є довірчий інтервал, який говорить нам про найбільш ймовірний інтервал, в якому буде лежати середнє значення або пропорція. Часто дається нижня і верхня межа довірчого інтервалу, але середина цих двох чисел є найкращим припущенням для того, що ми шукаємо. Припустимо, 95% довірчий інтервал для різниці між двома засобами становить -1,34 і 2,79. Знайдіть середину цих чисел, що є найкращим припущенням для різниці між двома засобами.

Рішення

Використовуємо формулу для середньої точки (Equation\ ref {midpoint}):

\[M\:=\:\frac{a+b}{2}=\:\frac{-1.34+2.79}{2} \nonumber\]

Тепер скористаємося калькулятором. Нам знадобляться круглі дужки навколо чисельника:

\[\left(-1.34+2.79\right)\div2\:=\:0.725 \nonumber\]

Таким чином, середина чисел -1,34 і 2,79 дорівнює 0,725.

Ескіз середньої точки на числовій лінії

Візуалізація середньої точки часто може виявити її набагато краще, ніж просто записати її значення. Діаграми мають принципове значення в статистиці.

Приклад\(\PageIndex{3}\)

Намалюйте точки -3, 5 та середину цих двох чисел на числовій лінії.

Рішення

Почнемо з пошуку середньої точки за формулою середньої точки (Equation\ ref {midpoint}):

\[M\:=\frac{\:-3+5}{2}=\left(-3+5\right)\div2\:=\:1 \nonumber\]

Тепер накидаємо ці три точки на числовій лінії:

числовий рядок з кінцевими точками -3 і 5 і середньою точкою 1

Приклад\(\PageIndex{4}\): hypothesis testing

Інше застосування середньої точки передбачає тестування гіпотез. Іноді нам дають гіпотезоване середнє значення, яке є серединою. Нам також дано середнє значення зразка, яке є або лівою, або правою кінцевою точкою. Мета полягає в тому, щоб знайти іншу кінцеву точку. Припустимо, що середня точка (гіпотезоване середнє значення) знаходиться на рівні 3.8, а права кінцева точка (середнє значення вибірки) дорівнює 5.1. Знайдіть значення лівої кінцевої точки.

Рішення

Це допомагає намалювати діаграму на числовій лінії, як показано нижче.

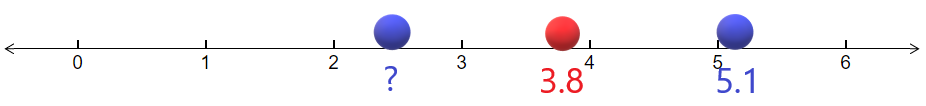
числовий рядок з невідомим, 3.8 і 5.1 нанесеним.

Тепер, оскільки 3.8 є середньою точкою, відстань від лівої кінцевої точки до середини дорівнює відстані від 3,8 до 5.1. Відстань від 3,8 до 5,1 становить:

\[5.1\:-\:3.8\:=\:1.3 \nonumber\]

Тому ліва кінцева точка знаходиться на 1,3 ліворуч від 3.8. Це можна знайти, віднімаючи два числа:

\[3.8\:-\:1.3\:=\:2.5 \nonumber\]

Тому ліва кінцева точка знаходиться на рівні 2,5.

Вправа

Припустимо, що середня точка (гіпотезована пропорція) знаходиться на рівні 0,31, а ліва кінцева точка (пропорція вибірки) - 0,28. Знайдіть значення правої кінцевої точки.