8: Площа Чі
- Page ID
- 97428
У розділі 5 була розроблена теорія висновків для категоріальних даних, заснована на біноміальному розподілі. Нагадаємо, що біноміальний розподіл показує ймовірність можливого числа успіхів у вибірці розміру n, коли було тільки два можливих незалежних результату: успіх і невдача. Що станеться, якщо існує більше двох можливих результатів?
Розглянемо наступні три питання.
- Чи генерує калькулятор TI 84 рівні числа 0-9 при використанні генератора випадкових цілих чисел?
- Робити щось щодо зміни клімату було викликом для людства. На веб-сайті Edge.Org була одна пропозиція, висунута Лі Смоліном, фізиком Інституту периметра та автором книги «Час відродження». (www.edge.org/розмова/дель... операція/ #rc 30 листопада 2013 р.) Суть пропозиції полягає в тому, що податок на вуглець повинен бути розміщений на весь вуглець, який використовується, але замість грошей, що надходять до уряду, він надходить на індивідуальні кліматичні пенсійні рахунки. У кожної людини був би такий рахунок. Кожен рахунок матиме дві категорії можливих інвестицій, які може вибрати фізична особа. Інвестиції категорії А полягають у речах, які пом'якшать зміни клімату (наприклад, сонячна енергія, вітер тощо). Інвестиції категорії B були б у речах, які могли б зробити добре, якщо зміни клімату не відбуватимуться (наприклад, комунальні послуги, які спалюють вугілля, прибережні розробки нерухомості та автомобільні компанії, які не виробляють економічні палива або електромобілі). Чи існує взаємозв'язок між думкою людини про зміну клімату та вибором інвестицій?
- Урагани відносяться до категорії 1,2,3,4,5. Чи відрізняється розподіл ураганів у 1951- 2000 роках, ніж це було в 1901-1950 роках?
Перш ніж зробити аналіз, необхідно зрозуміти тип даних, які збираються для кожного з цих питань.
У питанні 1 дані, які будуть зібрані, - це цифри 0, хоча 9. Хоча числа, як правило, вважаються кількісними, в цьому випадку ми просто хочемо знати, якщо калькулятор виробляє кожне конкретне число. Тому мова йде насправді про частоту, з якою ці цифри виробляються. Якщо процес, який використовується калькулятором, досить випадковий, то частоти для всіх чисел повинні бути рівними, якщо береться досить велика вибірка. Таким чином, незважаючи на те, що це кількісні дані, це насправді категоричні дані, з 10 різними категоріями і даними, що число було вибрано.
У питанні 2 уявіть собі опитування з двома питаннями, в якому люди задаються:
- Чи вважаєте ви, що зміни клімату відбуваються через те, що люди використовують джерела вуглецю, які призводять до збільшення парникових газів? Так Ні
- Що з наведених нижче найбільш уважно представляє вибір, який ви зробили б для ваших індивідуальних інвестицій в пенсійний рахунок клімату? Категорія A Категорія B
На це питання існує одна популяція. Кожна людина, яка приймає опитування, надасть дві відповіді. Мета полягає в тому, щоб визначити, чи існує кореляція між їхньою думкою про зміну клімату та їх інвестиційним вибором. Альтернативний спосіб сказати це те, що дві змінні або незалежні один від одного, а це означає, що одна відповідь не впливає на іншу, або вони не є незалежними, а це означає, що думка щодо зміни клімату та інвестиційна стратегія пов'язані.
У питанні 3 є дві популяції. Перша популяція - урагани в 1901-50 роках, а друга популяція - урагани в 1951-2000 роках. Існує 5 категорій ураганів, і мета полягає в тому, щоб побачити, чи розподіл ураганів у цих категоріях однаковий чи різний.
Задачі підходять до одного з наступних класів завдань, по порядку: доброзичливість придатності, тест на незалежність і тест на однорідність. Використання цих проблем і їх гіпотези наведені нижче.
- Goodness of Fit Тест
на доброту придатності використовується, коли категорична випадкова величина з більш ніж двома рівнями має очікуваний розподіл.
\(H_0\): Розподіл такий же, як очікувалося
\(H_1\): Розподіл відрізняється від очікуваного - Тест на
незалежність Тест на незалежність використовується, коли для однієї одиниці (або людини) є дві категоричні випадкові величини і мета полягає у визначенні кореляції між ними.
\(H_0\): Дві випадкові величини є незалежними (немає кореляції)
\(H_1\): Дві випадкові величини не є незалежними (кореляція)
Якщо дані є значними, ніж знання значення однієї з випадкових величин збільшує ймовірність пізнання значення іншої випадкової величини порівняно з випадковою. - Тест на однорідність
Тест на однорідність використовується, коли є зразки, взяті з двох (або більше) популяцій з метою визначити, чи є розподіл однієї випадкової величини подібним або різним у двох популяціях.
\(H_0\): Дві популяції однорідні
\(H_1\): дві популяції неоднорідніОскільки всі проблеми мають дані, які можна підрахувати рівно один раз, стратегія полягає в тому, щоб визначити, чим відрізняється розподіл рахунків від очікуваного розподілу. При аналізі всіх цих завдань використовується одна і та ж тестова статистика формула, яка називається\(chi ^2\) (Chi Square).
\[\chi^2 = \sum \dfrac{(O - E)^2}{E}\]
Розподіл, який використовується для перевірки гіпотез, - це сукупність\(chi ^2\) розподілів. Ці дистрибутиви позитивно перекошені. Вони не можуть бути негативними. Кожен розподіл заснований на кількості ступенів свободи. На відміну від t розподілів, в яких ступені свободи базувалися на розмірі вибірки\(chi ^2\), у випадку, ступеня свободи базуються на кількості рівнів випадкової величини (ів).
Наступні дистрибутиви показують 10 000 зразків розміром n = 100, в яких\(chi ^2\) тестова статистика обчислюється і графікується. Числа ступенів свободи в цих чотирьох графах - 1,2,5 і 9.
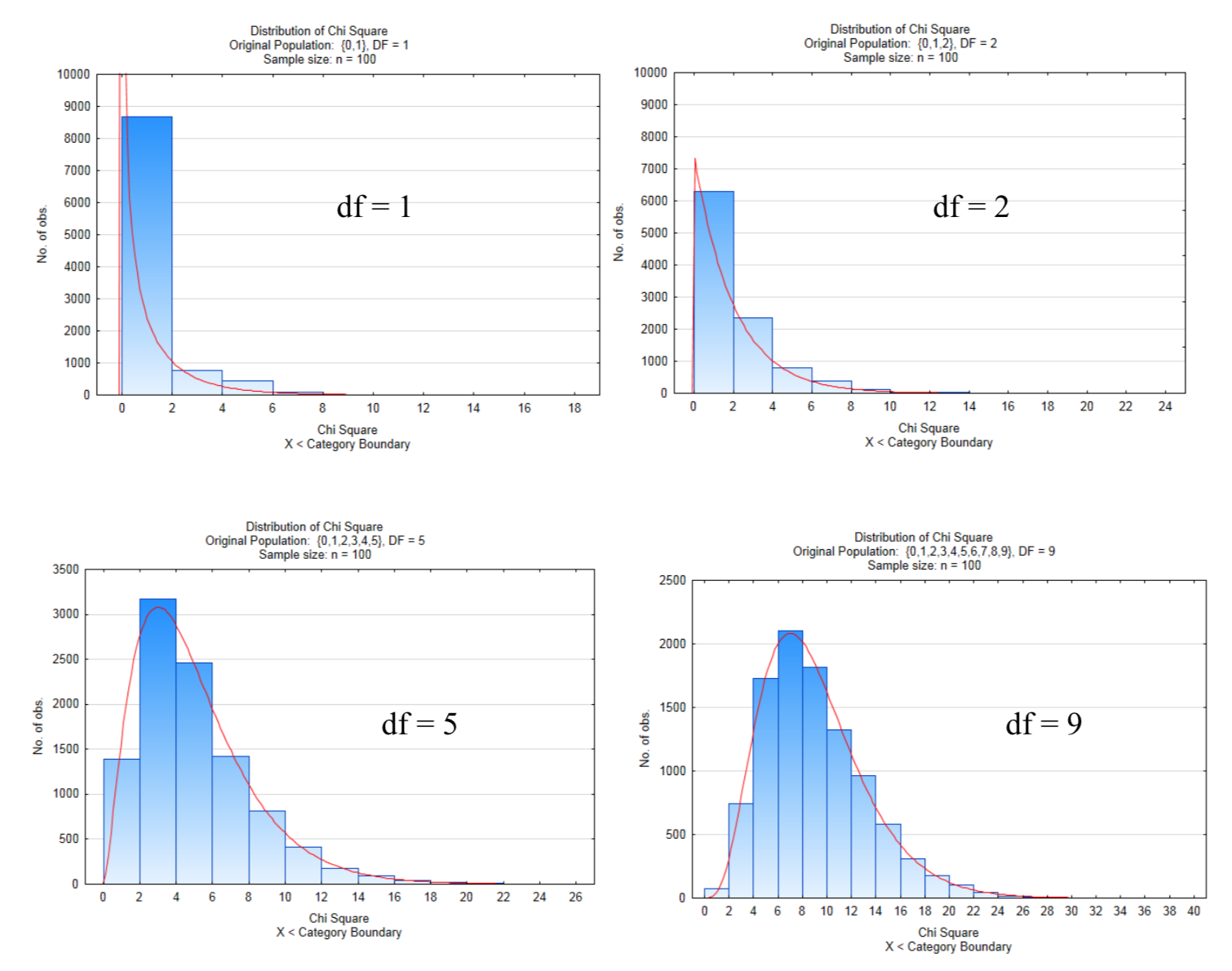
Зверніть увагу, як розподіл Chi Square стає менш перекошеним і наближається до нормального розподілу, коли кількість ступенів свободи збільшується. Збільшення кількості ступенів свободи відповідає збільшенню кількості рівнів пояснювального фактора. Спосіб знаходження ступенів свободи відрізняється за добротою придатності тесту порівняно з тестом на незалежність та тестом на однорідність. Кожен спосіб буде пояснений по черзі.
Тест на доброту придатності
1. Чи генерує калькулятор TI 84 рівні числа 0-9 при використанні генератора випадкових цілих чисел?
У цьому експерименті 12 чисел між 1 і 100 були випадковим чином генеруються калькулятором TI 84. Ці 12 чисел були використані як значення насіння. Після висіву калькулятора з кожним номером 10 нових чисел від 0 до 9 були згенеровані випадковим чином за допомогою функції randint на калькуляторі. Таким чином, було вироблено загалом 120 номерів між 0 і 9. Частота цих чисел показана в таблиці нижче.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 15 | 11 | 12 | 14 | 10 | 14 | 10 | 11 | 14 | 9 |
Гіпотези, що підлягають перевірці, такі:
\(H_0\): Спостережувана частота клітин дорівнює очікуваній частоті клітин для всіх клітин
\(H_1\): Спостережувана частота клітин не дорівнює очікуваній частоті клітин принаймні для однієї клітини. Використовуйте рівень значущості 0,05
Це можна уявити символічно як
\(H_0\):\(o_1 = \epsilon_1\) для всіх осередків
\(H_1\): принаймні\(o_1 \ne \epsilon_1\) для однієї клітинки
де - грецька буква omicron у нижньому регістрі, яка представляє спостережувану частоту клітин у базовій популяції, а ε - грецька буква епсилон у нижньому регістрі, яка представляє очікувану частоту клітин. Очікувана частота клітин завжди повинна бути 5 або вище. Якщо це не так, клітини слід перегрупувати.
У таблиці вище показані спостережувані частоти, але які очікувані частоти? Теоретично, якщо процес дійсно випадковий, то кожне число відбувалося б з однаковою частотою, якби вибірка була зроблена дуже велика кількість разів. Якщо це так, то в вибірці розміром 120, з 10 можливими альтернативами, очікувана кількість частот для кожної альтернативи має бути 12. З таблиці ми бачимо, що більшість частот не 12, але потрібен спосіб визначити, чи достатньо кількості варіацій, щоб припустити, що спостережувані частоти не дорівнюють очікуваним частотам. Такий висновок мав би на увазі, що калькулятор не виробляє воістину випадковий набір чисел. Стратегія полягає в тому, щоб знайти,\(\chi^2\) а потім використовувати відповідний\(\chi^2\) розподіл, щоб знайти p-значення. Один із способів знайти\(\chi^2 = \sum \dfrac{(O - E)^2}{E}\) - це таблиця.
| Спостерігається | Очікуваний | О - Е | \((O - E)^2\) | \(\dfrac{(O - E)^2}{E}\) |
|---|---|---|---|---|
| 15 | 12 | 3 | \ ((O - E) ^2\)» style="вертикальне вирівнювання: середина; "> 9 | \ (\ dfrac {(O - E) ^2} {E}\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{9}{12}\) |
| 11 | 12 | -1 | \ ((O - E) ^2\)» style="вертикальне вирівнювання: середина; "> 1 | \ (\ dfrac {(O - E) ^2} {E}\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{1}{12}\) |
| 12 | 12 | 0 | \ ((O - E) ^2\)» style="вертикальне вирівнювання: середина; "> 0 | \ (\ dfrac {(O - E) ^2} {E}\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{0}{12}\) |
| 14 | 12 | 2 | \ ((O - E) ^2\)» style="вертикальне вирівнювання: середина; "> 4 | \ (\ dfrac {(O - E) ^2} {E}\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{4}{12}\) |
| 10 | 12 | -2 | \ ((O - E) ^2\)» style="вертикальне вирівнювання: середина; "> 4 | \ (\ dfrac {(O - E) ^2} {E}\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{4}{12}\) |
| 14 | 12 | 2 | \ ((O - E) ^2\)» style="вертикальне вирівнювання: середина; "> 4 | \ (\ dfrac {(O - E) ^2} {E}\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{4}{12}\) |
| 10 | 12 | -2 | \ ((O - E) ^2\)» style="вертикальне вирівнювання: середина; "> 4 | \ (\ dfrac {(O - E) ^2} {E}\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{4}{12}\) |
| 11 | 12 | -1 | \ ((O - E) ^2\)» style="вертикальне вирівнювання: середина; "> 1 | \ (\ dfrac {(O - E) ^2} {E}\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{1}{12}\) |
| 14 | 12 | 2 | \ ((O - E) ^2\)» style="вертикальне вирівнювання: середина; "> 4 | \ (\ dfrac {(O - E) ^2} {E}\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{4}{12}\) |
| 9 | 12 | -3 | \ ((O - E) ^2\)» style="вертикальне вирівнювання: середина; "> 9 | \ (\ dfrac {(O - E) ^2} {E}\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{9}{12}\) |
| \ ((O - E) ^2\)» style="вертикальне вирівнювання: середина; "> | \ (\ dfrac {(O - E) ^2} {E}\)» style="вертикальне вирівнювання: середина; ">\(\chi^2 = \dfrac{40}{12} = 3.33\) |
Якщо r являє собою кількість рядків, то число ступенів свободи в тесті добра придатності дорівнює:
дф = р — 1.
Для цього тесту на доброту придатності є 10 рядків даних. Отже, існує 9 ступенів свободи.
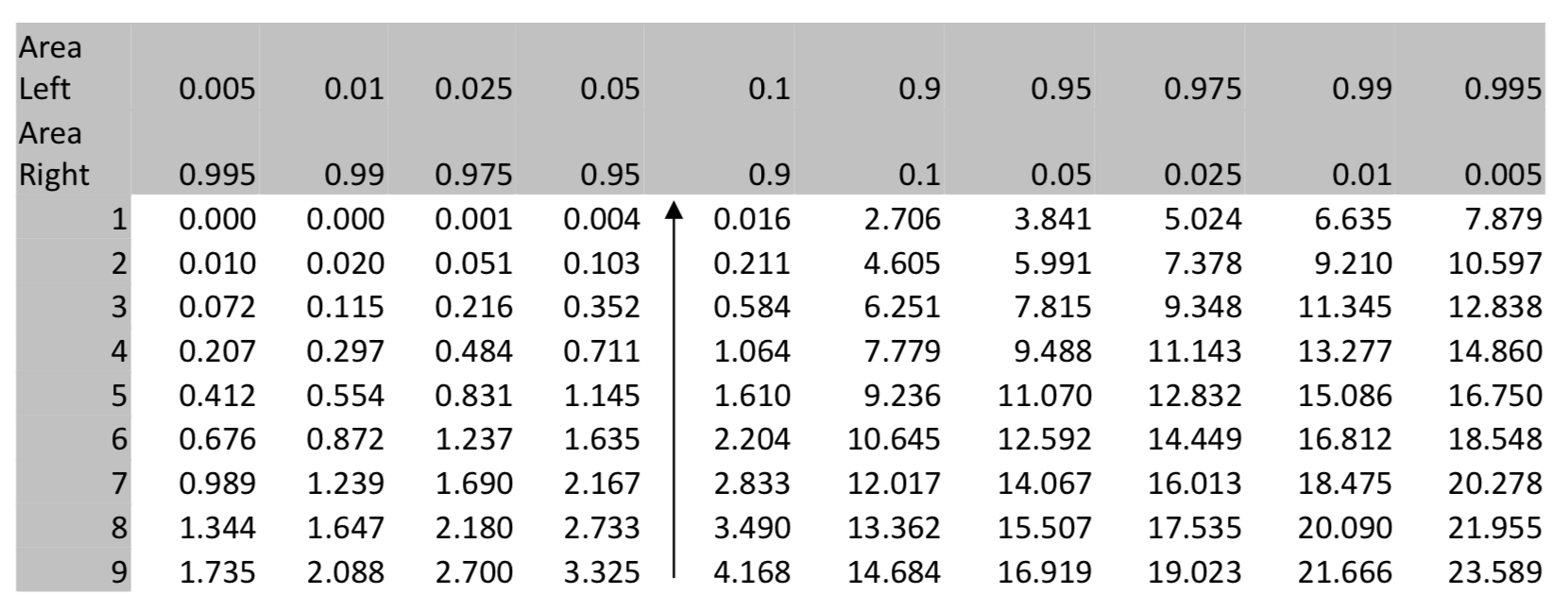
Значення p для\(\chi^2\) можна знайти за допомогою таблиці розподілів Chi Square в кінці цієї глави або вашого калькулятора.
Розподіли Chi-Square також можуть бути використані для пошуку p-значення. Використовуючи таблицю нижче, знайдіть ступінь свободи в лівому стовпчику, знайдіть\(\chi^2\) значення в рядку, потім перейдіть до рядка, який показує область праворуч, і використовуйте знак нерівності, щоб показати p-значення. Якщо p-значення більше\(\alpha\), то використовуйте символ більше ніж. Якщо він менше α, використовуйте символ менше ніж, але в будь-якому випадку використовуйте якомога більше точності. Наприклад, якщо α дорівнює 0,05, а площа праворуч менше 0,025, то p < 0,025 є кращим, ніж p < 0,05.
У цьому прикладі,\(\chi^2\) = 3.33, є 9 ступенів свободи, тому p-значення > 0,9.
\(\chi^2 = 3.33\)
Використання\(\chi^2\) cdf (низький, високий, df) в калькуляторі TI 84 призводить\(\chi^2\) до cdf (3.33, 1E99,9) = 0.9496.
Так як це p-значення явно вище 0,05, то висновок можна записати:
На рівні 5% значущості спостережувані значення осередків істотно не відрізняються від очікуваних значень осередків (\(\chi^2\)= 3,33, p = 0,9496, df = 9). Калькулятор TI84, здається, дає хороший набір випадкових цілих чисел.
У випадку з калькулятором, якщо він є випадковим у генерації чисел, ми очікуємо однакову кількість значень у кожній категорії. Тобто, ми очікуємо отримати однакову кількість 0 с, 1s, 2s тощо Оскільки вибірка складалася з 120 випробувань з 10 можливостями для кожного результату, очікуване значення становить 12, оскільки 120 ділиться на 10, дорівнює 12. Але що буде, якщо очікуваний результат у всіх випадках не однаковий?
Восени 2013 року наш коледж складався з 54% кавказьких, 14% латиноамериканців, 11% афроамериканців, 10% азіатських/тихоокеанських островів, 1% корінних американців, 3% міжнародних та 7% інших. Якби ми хотіли визначити, чи расово-етнічне розподіл учнів статистики відрізняється від всієї школи, ми могли б взяти опитування студентів статистики, щоб отримати спостережувані дані. Наведена нижче таблиця містить гіпотетичні спостережувані дані. Оскільки у вибірці 300 студентів, і на основі зарахування до коледжу 54% студентського тіла є білим, то очікувана кількість студентів у класі, які є білими, виявляється множенням 300 разів 0,54. Один і той же підхід застосовується для кожної гонки. Це показано в таблиці. Зверніть увагу, що загальна сума в очікуваному стовпці така ж, як у спостережуваному стовпці.
| Раса/етнічна приналежність | Спостерігається | Очікуваний |
|---|---|---|
| Кавказська/білий (54%) | 154 | 0.54 (300) = 162 |
| Іспанська/латиноамериканська (14%) | 48 | 0.14 (300) = 42 |
| Африканський американський/чорний (11%) | 36 | 0.1 (300) = 33 |
| Сианський/тихоокеанський житель (10%) | 35 | 0,10 (300) = 30 |
| Інший американець (1%) | 6 | 0,01 (300) = 3 |
| У міжнародному (33%) | 9 | 0.03 (300) = 9 |
| Інші типи розміщення (7%) | 12 | 0.07 (300) = 21 |
| Всього | 300 | Всього 300 |
Залишок добра fit тест робиться так само, як і на прикладі калькулятора і не буде продемонстрований тут.
Тест на незалежність Chi Square
Тест площі Чі на незалежність використовується, коли дослідник хоче визначити зв'язок між двома категоріальними випадковими величинами, зібраними на одній одиниці (або людині). Зразки питань включають:
- Чи існує зв'язок між релігійною приналежністю людини та її політичними партійними уподобаннями?
- Чи існує зв'язок між готовністю людини їсти генетично інженерну їжу та їх готовністю використовувати генно-інженерні ліки?
- Чи існує зв'язок між сферою навчання для випускника коледжу та їх здатністю критично мислити?
- Чи існує взаємозв'язок між якістю сну, який людина отримує, і їх ставленням протягом наступного дня?
Як приклад, ми дізнаємося механіку тесту на незалежність на гіпотетичному прикладі відповідей на два питання про зміну клімату та інвестиції.
- Чи вважаєте ви, що зміни клімату відбуваються через те, що люди використовують джерела вуглецю, які призводять до збільшення парникових газів? Так Ні
- Що з наведених нижче найбільш уважно представляє вибір, який ви зробили б для ваших індивідуальних інвестицій в пенсійний рахунок клімату? Категорія A Категорія B
Категорія A — сонячна, вітрова Категорія B - Вугілля, розвиток океану
\(H_0\): Дві випадкові величини є незалежними (без кореляції)
\(H_1\): Дві випадкові величини не є незалежними (кореляція)
Це також може бути зображено символічно як
\(H_0: o_1 = \epsilon_1\)для всіх клітин принаймні
\(H_1: o_1 \ne \epsilon_1\) для однієї клітинки,
де\(o\) є нижньою грецькою літерою omicron, яка представляє спостережувану частоту клітин в основній популяції і\(\epsilon\) є нижнім регістр грецька буква епсилон, яка представляє очікувану клітинку частоти. Очікувана частота клітин завжди повинна бути 5 або вище. Якщо це не так, клітини слід перегрупувати.
Використовуйте рівень значущості 0,05.
Оскільки це буде зроблено з даними прикиду, корисно буде зробити це двічі, щоразу роблячи протилежні висновки.
Дані будуть представлені в таблиці непередбачених ситуацій 2 х 2.
| Версія 1 Спостерігається |
Так - люди сприяють зміні клімату | Ні - люди не сприяють зміні клімату | Підсумки |
| Інвестиції категорії А (вітрові, сонячні) | 56 | 54 | |
| Категорія B Інвестиції (вугілля, розвиток берегів океану) | 47 | 43 | |
| Всього |
Тест на незалежність використовує ту ж формулу, що і добротність тесту на придатність. \(\chi^2 = \sum \dfrac{(O - E)^2}{E}\). На відміну від цього тесту, немає чіткого вказівки на те, які очікувані значення. Замість цього вони повинні бути розраховані, що являє собою чотириступінчастий процес.
Крок 1, Знайдіть підсумки рядків та стовпців та загальну суму.
| Версія 1 Спостерігається |
Так - люди сприяють зміні клімату | Ні - люди не сприяють зміні клімату | Підсумки |
| Інвестиції категорії А (вітрові, сонячні) | 56 | 54 | 110 |
| Категорія B Інвестиції (вугілля, розвиток берегів океану) | 47 | 43 | 90 |
| Всього | 103 | 97 | 200 |
Крок 2. Створіть нову таблицю для очікуваних значень. Процес міркування для обчислення очікуваних значень полягає в тому, щоб спочатку розглянути частку всіх значень, які потрапляють в кожен стовпець. У першому стовпці є 103 значення з 200, що є\(\dfrac{}{} = 0.515\). У другій колонці є 97 з 200 значень (0,485). Оскільки 51,5% значень знаходяться в першому стовпці, то можна було б очікувати, що 51,5% значень першого рядка також буде в першому стовпці. Таким чином, 0,515 (110) дає очікуване значення 56,65. Аналогічним чином, 0.485 (90) дасть очікуване значення 43.65 для останньої комірки. Як формула це може бути виражено у вигляді
\[\dfrac{Column\ Total}{Grand\ Total} \cdot Row\ Total\]
| Версія 1 Спостерігається |
Так - люди сприяють зміні клімату | Ні - люди не сприяють зміні клімату | Підсумки |
| Інвестиції категорії А (вітрові, сонячні) | \(\dfrac{103}{200} \cdot 110 = 56.65\) | \(\dfrac{97}{200} \cdot 110 = 53.35\) | 110 |
| Категорія B Інвестиції (вугілля, розвиток берегів океану) | \(\dfrac{103}{200} \cdot 90 = 46.35\) | \(\dfrac{97}{200} \cdot 110 = 43.65\) | 90 |
| Всього | 103 | 97 | 200 |
Крок 3. Використовуйте таблицю, подібну до тієї, яка використовується в тесті Goodness of Fit для обчислення площі Чі.
| Спостерігається | Очікуваний | \(O - E\) | \((O - E)^2\) | \(\dfrac{(O - E)^2}{E}\) |
| 56 | 56.65 | -0.65 | 0,4225 | 0,0075 |
| 54 | 53.35 | 0,65 | 0,4225 | 0.0079 |
| 47 | 46.35 | 0,65 | 0,4225 | 0,0091 |
| 43 | 43.65 | -0.65 | 0,4225 | 0,0097 |
| \(\chi^2 = 0.0342\) |
Крок 4. Визначте ступені свободи і знайдіть p-значення
Якщо R - кількість рядків у таблиці непередбачених обставин, а C - кількість стовпців у таблиці непередбачених обставин, то кількість ступенів свободи для тесту на незалежність визначається як
дф = (Р - 1) (С - 1).
Для таблиці непередбачених ситуацій 2 х 2, наприклад, у цій задачі, існує лише 1 ступінь свободи, оскільки (2-1) (2-1) = 1.
Значення p для\(\chi^2\) можна знайти за допомогою таблиці або калькулятора.
У таблиці знаходимо 0.034 в рядку з 1 ступенем свободи, потім рухаємося вгору до рядка для області праворуч. Оскільки площа праворуч більше 0,05, а точніше більше 0,1, то p-значення записується як p > 0,1.
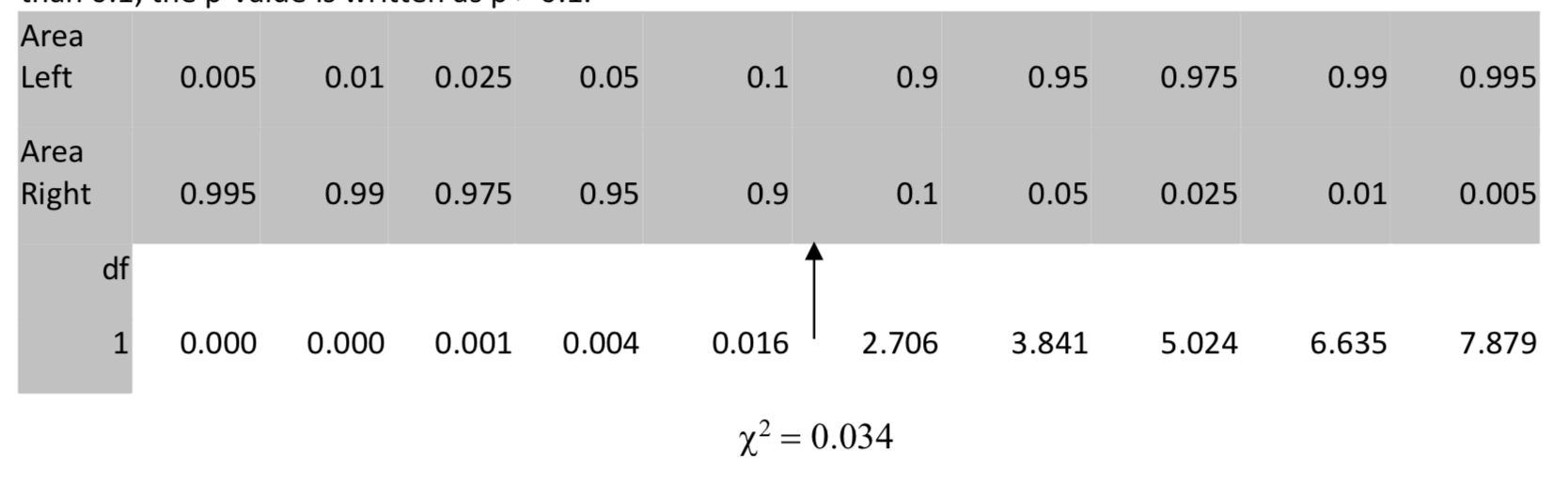
На калькуляторі використовуйте\(\chi^2\) cdf (низький, високий, df). В даному випадку\(\chi^2\) cdf (0,0342, 1Е99, 1) = 0,853.
Оскільки дані не є суттєвими, ми робимо висновок, що інвестиційна стратегія людей не залежить від їхньої думки про внесок людини в зміну клімату.
Версія 2 цієї проблеми використовує наступну таблицю непередбачених ситуацій.
| Версія 2 Спостерігається |
Так - люди сприяють зміні клімату | Ні - люди не сприяють зміні клімату | Підсумки |
| Інвестиції категорії А (вітрові, сонячні) | 80 | 30 | |
| Категорія B Інвестиції (вугілля, розвиток берегів океану) | 30 | 60 | |
| Всього |
Цього разу вся задача буде розрахована за допомогою калькулятора TI 84 замість побудови таблиць, які використовувалися у версії 1.
Крок 1. Матриця
Крок 2. Зробіть 1: [A] у матрицю 2 x 2, вибравши пункт Редагувати Enter, а потім змінити R x C за необхідності. Крок 3. Введіть частоти так, як вони наведені в таблиці.
Крок 4. STAT TESTS\(\chi^2\) − Тест
Спостерігається: [A]
Очікується: [B] (вам не потрібно створювати Очікувану матрицю, калькулятор буде для вас.)
Виберіть Обчислити, щоб побачити результати:
\(\chi^2\) = 31.03764922
p=2.5307155e-8
df=1
При цьому дані значні. Це означає, що існує взаємозв'язок між думкою кожної людини про внесок людини в зміну клімату та вибором інвестицій. Пам'ятайте, що кореляція - це не причинно-наслідковий зв'язок.
Тест Chi квадрат на однорідність
Третя і остання проблема стосується класифікації ураганів в два різних десятиліття, 1901-50 і 1951-2000 рр. Одна теорія про зміну клімату полягає в тому, що урагани можуть погіршити. працювати за допомогою таблиць.
Урагани класифікуються за шкалою ураганного вітру Саффіра-Сімпсона.2
Категорія 1 Постійні вітри 74-95 миль/год
Категорія 2 Постійні вітри 96-110 миль/год
Категорія 3 Постійні вітри 111-129 миль/год
Категорія 4 Постійні вітри 130-156 миль/год
Категорія 5 Постійні вітри 157 або вище.
Урагани 3, 4 і 5 категорії вважаються основними.
Ця проблема буде
Інтерес населення представляє розподіл ураганів за сформованими в той час кліматичними умовами. Гіпотези, що перевіряються, є
\(H_0\): Розподіли однорідні
\(H_1\): Розподіли неоднорідні
Це також може бути зображено символічно як
\(H_0: o_1 = \epsilon_1\)для всіх осередків принаймні
\(H_1: o_1 \ne \epsilon_1\) для однієї клітинки
де\(o\) - нижня грецька буква omicron, яка представляє спостережувану частоту клітин у базовій популяції та\(\epsilon\) є нижньою грецькою літерою epsilon, яка представляє очікувану частоту клітин. Очікувана частота клітин завжди повинна бути 5 або вище. Якщо це не так, клітини слід перегрупувати.
Таблиця непередбачених ситуацій 5 х 2 буде використана для показу частот, які спостерігалися. Очікувані частоти розраховувалися так само, як і при випробуванні на незалежність. (http://www.nhc.noaa.gov/pastdec.shtml переглянуто 12/7/13)
| Спостерігається | 1901 - 1950 | 1951 - 2000 | Підсумки |
| 1 категорія | 37 | 29 | 66 |
| Категорія 2 | 24 | 15 | 39 |
| категорія 3 | 26 | 21 | 47 |
| категорія 4 | 7 | 5 | 12 |
| категорія 5 | 1 | 2 | 3 |
| Підсумки | 95 | 72 | 167 |
| Очікуваний | 1901 - 1950 | 1951 - 2000 | Підсумки |
| 1 категорія | 37.54 | 28.46 | 66 |
| Категорія 2 | 22.19 | 16.81 | 39 |
| категорія 3 | 26.74 | 20.26 | 47 |
| категорія 4 | 6.83 | 5.17 | 12 |
| категорія 5 | 1.71 | 1.29 | 3 |
| Підсумки | 95 | 72 | 167 |
Зверніть увагу, що очікувані частоти клітин для ураганів категорії 5 менше 5, тому нам доведеться переробити цю проблему, об'єднавши групи. Група 5 буде об'єднана з групою 4 і будуть надані змінені таблиці.
| Спостерігається | 1901 - 1950 | 1951 - 2000 | Всього |
| 1 категорія | 37 | 29 | 66 |
| Категорія 2 | 24 | 15 | 39 |
| категорія 3 | 26 | 21 | 47 |
| Категорія 4 та 5 | 8 | 7 | 15 |
| Всього | 95 | 72 | 167 |
| Спостерігається | 1901 - 1950 | 1951 - 2000 | Всього |
| 1 категорія | 37.54 | 28.46 | 66 |
| Категорія 2 | 22.19 | 16.81 | 39 |
| категорія 3 | 26.74 | 20.26 | 47 |
| Категорія 4 та 5 | 8.53 | 6.47 | 15 |
| Всього | 95 | 72 | 167 |
| Спостерігається | Очікуваний | \(O - E\) | \((O - E)^2\) | \(\dfrac{(O - E)^2}{E}\) | |
| 1901 - 50 | |||||
| Категорія 1 | 37 | 37.54 | -0.54 | 0,30 | 0,008 |
| Категорія 2 | 24 | 22.19 | 1.81 | 3.29 | 0,148 |
| категорія 3 | 26 | 26.74 | -0.74 | 0,54 | 0,020 |
| Категорія 4 та 5 | 8 | 8.53 | -0.53 | 0,28 | 0,033 |
| 1951 - 2000 | |||||
| Категорія 1 | 29 | 28.46 | 0,54 | 0,30 | 0,010 |
| Категорія 2 | 15 | 16.81 | -1.81 | 3.29 | 0.196 |
| категорія 3 | 21 | 20.26 | 0,74 | 0,54 | 0.027 |
| Категорія 4 та 5 | 7 | 6.47 | 0,53 | 0,28 | 0,044 |
| \(\chi^2 = 0.487\) |
Якщо R - кількість рядків у таблиці непередбачених обставин, а C - кількість стовпців у таблиці непередбачених обставин, то кількість ступенів свободи для тесту на однорідність визначається як
дф = (Р-1) (С-1).
Для таблиці непередбачених ситуацій 4\(\times\) 2, як у цій задачі, існує 3 ступеня свободи, оскільки (4-1) (2-1) = 3 ступеня свободи.
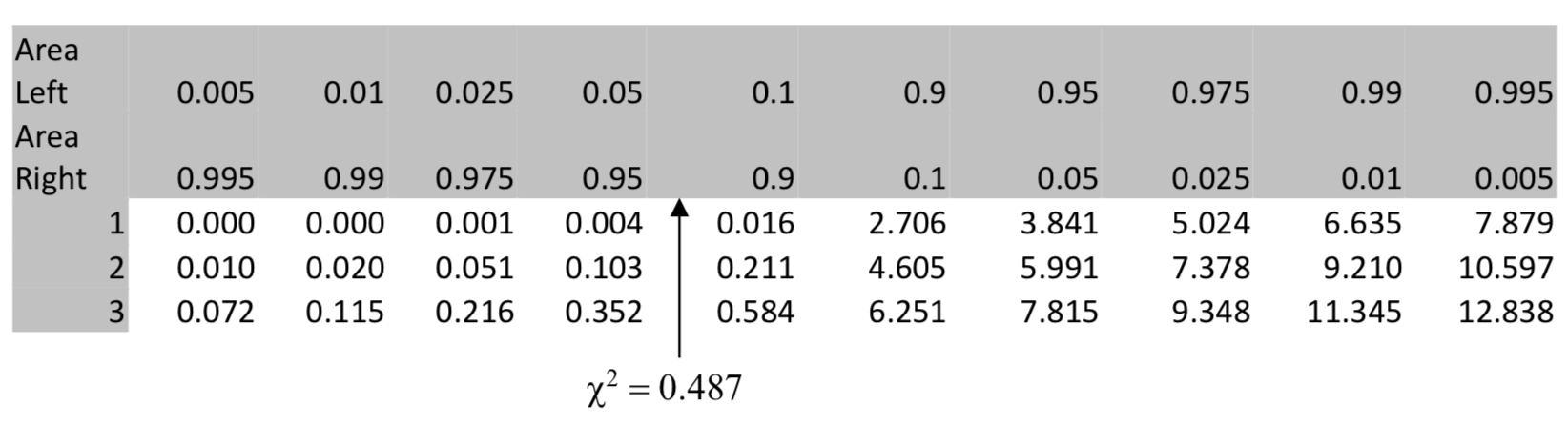
У таблиці показано p-значення менше 0,05. Калькулятор підтверджує це тому,\(\chi^2\) що cdf (0.486, 1E99, 3) = 0.9218. Отже, висновок полягає в тому, що немає суттєвої різниці між розподілом ураганів у 1951-2000 роках і 1901-50 роках.
Розмежування використання тесту на незалежність і однорідність
Хоча математика, що стоїть за тестом на незалежність і тест на однорідність, однакові, намір їх використання та інтерпретації результатів відрізняється.
Тест на незалежність використовується, коли для кожної одиниці визначаються дві випадкові величини, обидві з яких вважаються змінними відгуку. Тест на однорідність використовується, коли однією з випадкових величин є пояснювальна величина і суб'єкти вибираються виходячи з їх рівня цієї змінної. Інша випадкова величина - це змінна відповіді.
Визначення того, який тест використовувати, встановлюється підходом відбору проб. Якщо заздалегідь чітко визначені дві популяції і проводиться випадковий відбір з кожної популяції, то популяції будуть порівнюватися за допомогою тесту на однорідність. Якщо не докладено зусиль, щоб заздалегідь розрізнити популяції, і з цієї популяції проводиться випадковий вибір, а потім визначаються значення двох випадкових величин, тест на незалежність є доречним.
Приклад може прояснити тонку різницю між двома тестами. Розглянемо одну випадкову величину, щоб бути перевагою людини між бігом і плаванням для фізичних вправ, а іншу випадкову величину - перевагу людини між переглядом телевізора або читанням книги. Якщо дослідник випадковим чином вибирає деяких бігунів і деяких плавців і запитує кожну групу про їх перевагу телевізору або читання книги, тест на однорідність буде доречним. З іншого боку, якщо дослідник опитування випадково відібраних людей і запитує, чи вони віддають перевагу бігу чи плаванню, і якщо вони віддають перевагу телевізору чи читанню, то метою буде визначити, чи існує кореляція між цими двома випадковими величинами за допомогою тесту на незалежність.
| Chi - Квадратні розподіли | ||||||||||
| Зона ліворуч | 0,005 | 0,01 | 0,025 | 0,05 | 0.1 | 0.9 | 0,95 | 0,975 | 0,99 | 0,995 |
| Область праворуч | 0,995 | 0,99 | 0,975 | 0,95 | 0.9 | 0.1 | 0,05 | 0,025 | 0,01 | 0,005 |
| дф | ||||||||||
| 1 | 0.000 | 0.000 | 0,001 | 0,004 | 0,016 | 2.706 | 3.841 | 5.024 | 6.635 | 7,879 |
| 2 | 0,010 | 0,020 | 0,051 | 0.103 | 0.211 | 4.605 | 5.991 | 7.378 | 9.210 | 10.597 |
| 3 | 0.072 | 0,115 | 0,216 | 0,352 | 0,584 | 6.251 | 7.815 | 9.348 | 11.345 | 12.838 |
| 4 | 0,207 | 0,287 | 0,484 | 0,711 | 1.064 | 7.779 | 9.488 | 11.143 | 13.277 | 14 860 |
| 5 | 0,412 | 0,554 | 0,831 | 1.145 | 1.610 | 9.236 | 11.070 | 12.832 | 15.086 | 16.750 |
| 6 | 0.676 | 0,872 | 1.237 | 1,635 | 2.204 | 10.645 | 12.592 | 14.449 | 16.812 | 18 548 |
| 7 | 0,989 | 1.239 | 1,690 | 2.167 | 2.833 | 12.017 | 14.067 | 16.013 | 18.475 | 20.278 |
| 8 | 1,344 | 1,647 | 2.180 | 2.733 | 3 490 | 13.362 | 15.507 | 17.535 | 20.090 | 21.955 |
| 9 | 1.735 | 2.088 | 2.700 | 3.325 | 4.168 | 14.684 | 16.919 | 19.023 | 21.666 | 23.589 |
| 10 | 2.156 | 2.558 | 3.247 | 3.940 | 4.865 | 15.987 | 18.307 | 20.483 | 23.209 | 25.188 |
| 11 | 2.603 | 3.053 | 3.816 | 4.575 | 5.578 | 17.275 | 19.675 | 21.920 | 24.725 | 26.757 |
| 12 | 3.074 | 3.571 | 4.404 | 5.226 | 6.304 | 18.549 | 21.026 | 23.337 | 26.217 | 28.300 |
| 13 | 3.565 | 4.107 | 5.009 | 5.892 | 7.041 | 19.812 | 22.362 | 24.736 | 27.688 | 29.819 |
| 14 | 4.075 | 4.660 | 5.629 | 6.571 | 7.790 | 21/064 | 23.685 | 26.119 | 29.141 | 31.319 |
| 15 | 4.601 | 5.229 | 6.262 | 7.261 | 8.547 | 22.307 | 24.996 | 27.488 | 30.578 | 32.801 |
| 16 | 5.142 | 5 812 | 6.908 | 7,962 | 9.312 | 23.542 | 26.296 | 28.845 | 32.000 | 34.267 |
| 17 | 5.697 | 6.408 | 7.564 | 8.672 | 10.085 | 24.769 | 27.587 | 30.191 | 33.409 | 35.718 |
| 18 | 6.265 | 7.015 | 8.231 | 9.390 | 10,865 | 25.989 | 28.869 | 31.526 | 34.805 | 37.156 |
| 19 | 6.844 | 7.633 | 8.907 | 10.117 | 11 651 | 27.204 | 30.144 | 32.852 | 36.191 | 38.582 |
| 20 | 7.434 | 8.260 | 9.591 | 10.851 | 12.443 | 28.412 | 31.410 | 34.170 | 37.566 | 39.997 |
| 21 | 8.034 | 8.897 | 10.283 | 11.591 | 13.240 | 29.615 | 32.671 | 35.479 | 38.932 | 41.401 |
| 22 | 8.643 | 9.542 | 10,982 | 12.338 | 14.041 | 30.813 | 33.924 | 36.781 | 40.289 | 42.796 |
| 23 | 9.260 | 10.196 | 11.689 | 13.091 | 14 848 | 32.007 | 35.172 | 38.076 | 41.638 | 44.181 |
| 24 | 9.886 | 10.856 | 12.401 | 13 848 | 15.659 | 33.196 | 36.415 | 39.365 | 42.980 | 45.558 |
| 25 | 10.520 | 11.524 | 13.120 | 14.611 | 16.473 | 34.382 | 37.652 | 40.646 | 44.314 | 46.928 |
| 26 | 11.160 | 12.198 | 13,844 | 15.379 | 17.292 | 35.563 | 38.885 | 41.923 | 45.642 | 48.290 |
| 27 | 11.808 | 12.878 | 14.573 | 16.151 | 18.114 | 36.741 | 40.113 | 43.195 | 46.963 | 49.645 |
| 28 | 12.461 | 13,565 | 15.398 | 16.928 | 18.939 | 37.916 | 41.337 | 44.461 | 48.278 | 50.994 |
| 29 | 13.121 | 14.256 | 16.047 | 17.708 | 19.768 | 39.087 | 42.557 | 45.722 | 49.588 | 52.335 |
| 30 | 13,787 | 14,953 | 16.791 | 18 493 | 20.599 | 40.256 | 43.773 | 46.979 | 50.892 | 53.672 |
| 40 | 20.707 | 22.164 | 24.433 | 26.509 | 29.051 | 51.805 | 55.758 | 59.342 | 63.691 | 66.766 |
| 50 | 27.991 | 29.707 | 32.357 | 34.764 | 37.689 | 63.167 | 67.505 | 71.420 | 76.154 | 79.490 |
| 60 | 35.534 | 37.485 | 40.482 | 43.188 | 46.459 | 74.397 | 79.082 | 83.298 | 88.379 | 91.952 |
| 70 | 43.275 | 45.442 | 48.758 | 51.739 | 55.329 | 85.527 | 90.531 | 95.023 | 100.425 | 104.215 |
| 80 | 51.172 | 53.540 | 57.153 | 60.391 | 64.278 | 96.578 | 101.879 | 106.629 | 112.329 | 116.321 |
| 90 | 59.196 | 61.754 | 65.647 | 69.126 | 73.291 | 107.565 | 113,145 | 118.136 | 124.116 | 128.299 |
| 100 | 67.328 | 70.065 | 74.222 | 77.929 | 82.358 | 118 498 | 124.342 | 129.561 | 135.807 | 140.170 |
| 110 | 75.550 | 78.458 | 82.867 | 86.792 | 91.471 | 129.385 | 135.480 | 140.916 | 147.414 | 151.948 |
