Skip to main content
LibreTexts - Ukrayinska

4.4: Нормальність

  1. Last updated
  2. Save as PDF
  • Page ID
    97559

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Як вирішити, який тест використовувати, параметричний або непараметричний, t-тест або Wilcoxon? Нам потрібно знати, чи слід розподіл або принаймні наближається до нормальності. Це можна перевірити візуально (рис.\(\PageIndex{1}\)):

    Код\(\PageIndex{1}\) (R):

    salary <- c(21, 19, 27, 11, 102, 25, 21)
new.1000 <- sample((median(salary) - IQR(salary)) : + (median(salary) + IQR(salary)), 1000, replace=TRUE)
salary2 <- c(salary, new.1000)
qqnorm(salary2, main=""); qqline(salary2, col=2)

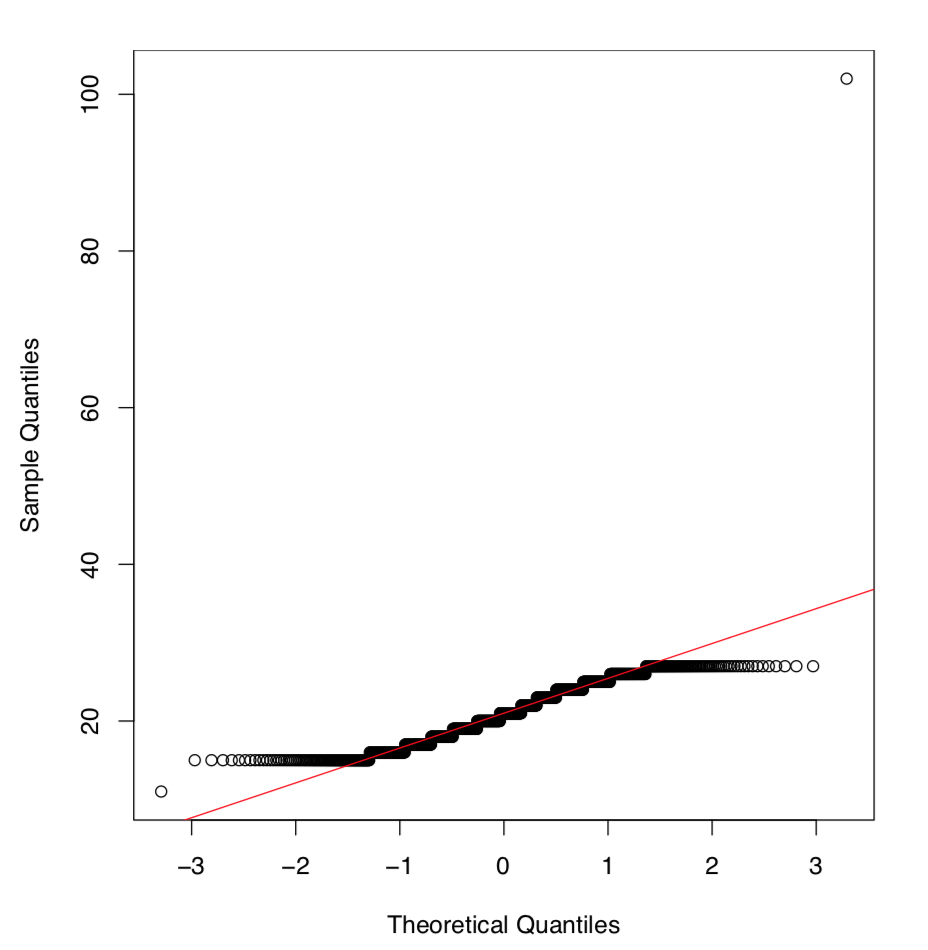
    Як працює сюжет QQ? По-перше, точки даних впорядковуються, і кожна з них присвоюється квантилі. По-друге, обчислюється набір теоретичних квантиль - позицій, які точки даних повинні були займати при нормальному розподілі. Нарешті, теоретичні та емпіричні квантилі парні та побудовані.

    Ми обклали сюжет лінією, що йде крізь квартилі. Коли точки уважно слідують за лінією, емпіричний розподіл є нормальним. Тут багато точок у хвостів далеко. Знову ж таки, робимо висновок, що оригінальний розподіл не є нормальним.

    R також пропонує числові прилади, які перевіряють нормальність. Перший з них - тест Шапіро-Вілка (будь ласка, запустіть цей код самостійно):

    Код\(\PageIndex{2}\) (R):

    salary <- c(21, 19, 27, 11, 102, 25, 21)
new.1000 <- sample((median(salary) - IQR(salary)) : + (median(salary) + IQR(salary)), 1000, replace=TRUE)
salary2 <- c(salary, new.1000)
shapiro.test(salary)
shapiro.test(salary2)

    Тут вихід досить короткий. P-значення невеликі, але якою була нульова гіпотеза? Навіть вбудована довідка про це не констатує. Щоб зрозуміти, ми можемо провести простий експеримент:

    Код\(\PageIndex{3}\) (R):

    set.seed(1638) # freeze random number generator
shapiro.test(rnorm(100))

    Команда rnorm () генерує випадкові числа, які слідують за нормальним розподілом, стільки ж з них, як зазначено в аргументі. Тут ми отримали p-значення, що наближається до одиниці. Зрозуміло, що нульова гіпотеза була «емпіричний розподіл є нормальним».

    Знімок екрана 2019-01-09 в 9.57,17 PM.png
    Малюнок\(\PageIndex{1}\) Графічна перевірка на нормальність.

    Озброївшись цим невеликим експериментом, ми можемо зробити висновок, що розподіли як зарплати, так і зарплату2 не є нормальними.

    Колмогорова-Смирнова тест працює з двома дистрибутивами. Нульова гіпотеза полягає в тому, що обидва зразки надходили з однієї популяції. Якщо ми хочемо перевірити один розподіл проти нормального, другим аргументом має бути pnorm:

    Код\(\PageIndex{4}\) (R):

    salary <- c(21, 19, 27, 11, 102, 25, 21)
new.1000 <- sample((median(salary) - IQR(salary)) : + (median(salary) + IQR(salary)), 1000, replace=TRUE)
salary2 <- c(salary, new.1000)
ks.test(scale(salary2), "pnorm")

    (Результат можна порівняти з результатом тесту Шапіро-Вілка. Ми масштабували дані, тому що за замовчуванням другий аргумент використовує масштабований нормальний розподіл.)

    Функція ks.test () приймає будь-який тип другого аргументу і тому може бути використана для перевірки надійності наближення розподілу струму з будь-яким теоретичним розподілом, не обов'язково нормальним. Однак тест Колмогорова-Смирнова часто повертає невірну відповідь для зразків, який розмір\(< 50\), тому він менш потужний, ніж тест Шапіро-Вілкса.

    2.2e-16 ми так звані експоненціальні позначення, спосіб показати дійсно малі числа, як цей (\(2.2 \times 10^{-16}\)). Якщо це позначення вам не влаштовує, є спосіб позбутися від нього:

    Код\(\PageIndex{5}\) (R):

    salary <- c(21, 19, 27, 11, 102, 25, 21)
new.1000 <- sample((median(salary) - IQR(salary)) : + (median(salary) + IQR(salary)), 1000, replace=TRUE)
salary2 <- c(salary, new.1000)
old.options <- options(scipen=100)
ks.test(scale(salary2), "pnorm")
options(old.options)

    (Опція scipen дорівнює максимально допустимій кількості нулів.)

    Найчастіше ці три способи визначення нормальності узгоджуються, але це не дивно, якщо вони повертають різні результати. Перевірка нормальності - це не смертний вирок, це всього лише думка, заснована на ймовірності.

    Знову ж таки, якщо розмір вибірки невеликий, статистичні тести і навіть квантильно-квантильні ділянки часто не виявляють ненормальності. У цих випадках простіші інструменти, такі як стовбурова ділянка або гістограма, нададуть кращу допомогу.