Глосарій
- Page ID
- 98003
Цілі навчання
- Визначення різних термінів, що зустрічаються у всьому підручнику
Апріорне порівняння/Планове порівняння
Порівняння, яке планується перед проведенням експерименту або принаймні до вивчення даних. Також називається апріорним порівнянням.
Абсолютне відхилення/Абсолютна різниця
Абсолютне значення різниці між двома числами. Абсолютне відхилення між\(5\) і\(3\) є\(2\); між\(3\) і\(5\) є\(2\);\(-4\) і між і\(2\) є\(6\).
Альтернативна гіпотеза
При перевірці гіпотез висувається нульова гіпотеза і альтернативна гіпотеза. Якщо дані досить сильні, щоб відкинути нульову гіпотезу, то нульова гіпотеза відкидається на користь альтернативної гіпотези. Наприклад, якщо нульова гіпотеза полягала в тому, що\(μ_1= μ_2\) тоді альтернативна гіпотеза (для двоххвостого тесту) була б\(μ_1 ≠ μ_2\).
Аналіз дисперсії
Аналіз дисперсії - це метод перевірки гіпотез про засоби. Це найбільш широко використовуваний метод статистичного висновку для аналізу експериментальних даних.
Анти-лог
Беручи антилог номера скасовує операцію взяття журналу. Тому, оскільки\(\log_{10}(1000)= 3\),\(antilog_{10}\) of\(3\) is\(1,000\) .Taking анти-лог числа скасовує операцію взяття журналу. Тому, з тих пір\(\log_{10}(1000)= 3\),\(antilog_{10}\) of\(3\) is\(1,000\). Беручи антилог\(X\) піднімає основу логарифма, про який йде мова\(X\).
Середній
- (арифметичне) середнє
- Будь-яка міра центральної тенденції
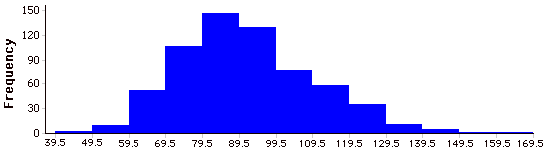
Гістограма
Графічний метод подання даних. Для кожного рівня змінної малюється смуга. Висота кожного бару містить значення змінної. Гістограми корисні для відображення таких речей, як кількість частот і відсотки збільшення. Вони не рекомендуються для відображення засобів (незважаючи на поширену практику), оскільки графіки коробки представляють більше інформації в тій же кількості простору.
Приклад гістограми наведено нижче.
Базова ставка
Справжня частка населення, що має певний стан, атрибут або захворювання. Наприклад, частка людей з шизофренією становить приблизно\(0.01\). Дуже важливо враховувати базову ставку при класифікації людей. Як то кажуть, «якщо ви чуєте копита, думайте, що кінь не зебра», оскільки ви частіше зіткнетеся з конем, ніж зеброю (принаймні в більшості місць).
Теорема Байєса
Теорема Байєса враховує як попередню ймовірність події, так і діагностичне значення тесту для визначення задньої ймовірності події. Теорема показана нижче:
\[P(D\mid T) = \frac{P(T\mid D)P(D)}{P(T\mid D)P(D)+P(T\mid D')P(D')}\]
де\(P(D|T)\) задня ймовірність умови\(D\) заданого результату тесту\(T\),\(P(T|D)\) є умовною ймовірністю\(T\) заданої\(D\),\(P(D)\) є попередньою ймовірністю\(D\),\(P(T|D')\) є умовною ймовірністю\(T\) даного не\(D\) , І\(P(D')\) є ймовірність того, що ні\(D'\).
Бета-каротин
Людський організм перетворює бета-каротин у вітамін\(A\), необхідний компонент наших дієт. Багато овочів, таких як морква, є хорошими джерелами бета-каротину. Дослідження показали, що бета-каротин добавки можуть забезпечити цілий ряд переваг для здоров'я, починаючи від просування здорових очей до запобігання раку. Інші дослідження показали, що добавки бета-каротину можуть збільшити захворюваність на рак.
Бета-вага
Стандартизований коефіцієнт регресії.
Між суб'єктами Фактор/Між суб'єктами Змінна
Міжпредметні змінні - це незалежні змінні або фактори, в яких для кожного рівня змінної використовується різна група суб'єктів. Якщо проводиться експеримент, порівнюючи чотири методи викладання словникового запасу і якщо для кожного з чотирьох методів навчання використовується різна група предметів, то метод навчання є змінною між предметами.
Між суб'єктами Фактор/Між суб'єктами Змінна
Міжпредметні змінні - це незалежні змінні або фактори, в яких для кожного рівня змінної використовується різна група суб'єктів. Якщо проводиться експеримент, порівнюючи чотири методи викладання словникового запасу і якщо для кожного з чотирьох методів навчання використовується різна група предметів, то метод навчання є змінною між предметами.
Упередженість
- Метод вибірки є упередженим, якщо кожен елемент не має рівних шансів на вибір. Зразок користувачів Інтернету виявив, що читання онлайн статистика книга буде упередженим зразком всіх користувачів Інтернету. Випадкова вибірка є неупередженою. Зверніть увагу, що можливий ухил відноситься до методу вибірки, а не до результату. Неупереджений метод може випадково призвести до дуже нерепрезентативної вибірки.
- Оцінювач є упередженим, якщо він систематично завищує або занижує параметр, який він оцінює. Іншими словами, він є упередженим, якщо середнє значення розподілу вибірки статистики не є параметром, який він оцінює, вибіркове середнє - це неупереджена оцінка середнього чисельності населення. Середнє квадратичне відхилення вибіркових балів від їх середнього є упередженою оцінкою дисперсії, оскільки вона має тенденцію занижувати дисперсію популяції.
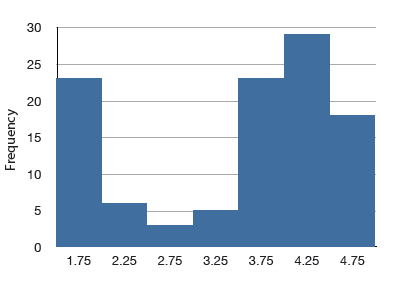
Бімодальний розподіл
Розподіл з двома чіткими піками. Приклад наведено нижче.
Біноміальний розподіл
Розподіл ймовірностей для незалежних подій, для яких є лише два можливі результати, такі як переворот монети. Якщо один з двох результатів визначається як успіх, то ймовірність рівно х успіхів з\(N\) випробувань (подій) задається:
\[P(x) = \frac{N!}{x!(N-x)!}\pi ^x(1-\pi )^{N-x}\]
Двоваріантний
Біваріативні дані - це дані, для яких існує дві змінні для кожного спостереження. Як приклад наведені нижче двоваріантні дані показують вік чоловіків і дружин\(10\) подружніх пар.
| Чоловік | 36 | 72 | 37 | 36 | 51 | 50 | 47 | 50 | 37 | 41 |
| Дружина | 35 | 67 | 33 | 35 | 50 | 46 | 47 | 42 | 36 | 41 |
Корекція Бонферроні
Загалом, щоб зберегти familywise rate помилок (\(FER\)) на рівні або нижче\(0.05\), коефіцієнт помилок для порівняння (\(PCER\)) повинен бути:\[PCER = 0.05/c\] де\(c\) кількість порівнянь. Більш загально, щоб застрахувати,\(FER\) що значення менше або дорівнює альфа, використовуйте\[PCER = alpha/c\]
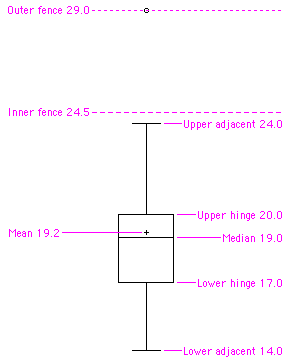
Коробка Ділянка
Одне з найбільш ефективних графічних резюме набору даних, діаграма коробки, як правило, показує середнє, медіану\(25^{th}\)\(75^{th}\) та процентилі та викиди. Стандартний графік коробки складається з медіани, верхнього шарніра, нижнього шарніра, верхнього сусіднього значення, нижнього сусіднього значення, зовнішніх значень та далеких значень. Приклад наведено нижче. Паралельні графіки коробки дуже корисні для порівняння розподілів. Дивись ще: крок, Н-спред.
Центр (розподілу) /Центральна Тенденція
Центр або середина розподілу. Існує багато заходів центральної тенденції. Найбільш поширеними є середній, медіанний, і, режим. Інші включають тримеанське, обрізане середнє та середнє геометричне.)
Клас частоти
Однією зі складових гістограми, частотою класів є кількість спостережень у кожному класовому інтервалі.
Інтервал класу/ширина бункера
Також відомий як ширина біна, інтервал класів є поділом даних для використання в гістограмі. Наприклад, можна розділити бали на\(100\) точковому тесті на класи інтервалів\(1-25\)\(26-49\),\(50-74\) і\(75-100\).
Порівняння між засоби/ Контрастність між засобами
Спосіб перевірки відмінностей між засобами на значущість. Наприклад, можна перевірити, чи різниця між\(\text{Mean 1}\) середнім значенням\(\text{Mean 2}\) і суттєво\(\text{Mean 3}\) відрізняється.
Умовна ймовірність
Імовірність, що\(\text{event A}\) виникає з огляду на те, що\(\text{event B}\) вже відбулося, називається умовною ймовірністю\(A\) даного\(B\). Символічно це пишеться як\(P(A|B)\). Імовірність дощу в понеділок, враховуючи, що в неділю йшов дощ, буде написана як\(\text{P(Rain on Monday | Rain on Sunday)}\).
Довірчий інтервал
Довірчий інтервал - це діапазон балів, які можуть містити оцінюваний параметр. Інтервали можуть бути побудовані так, щоб більш-менш імовірно містити параметр:\(95\%\)\(95\%\) довірчих інтервалів містять оцінюваний параметр, тоді як\(99\%\)\(99\%\) довірчі інтервали містять оцінюваний параметр. Чим ширше довірчий інтервал, тим більше невизначеності щодо значення параметра.
заплутаний
Дві або більше змінних плутаються, якщо їх ефекти не можуть бути розділені, оскільки вони змінюються разом. Наприклад, якщо дослідження про вплив світла ненавмисно маніпулювало теплом разом зі світлом, то світло і тепло були б заплутані.
Кука D
D Кука - це міра впливу спостереження в регресії і пропорційна сумі квадратних відмінностей між прогнозами, зробленими з усіма спостереженнями в аналізі та прогнозами, зробленими, залишаючи розглянуте спостереження.
Постійна
Значення, яке не змінюється. Такі значення, як пі, або маса Землі, є константами. Порівняйте зі змінними.
Безперервні змінні
Змінні, які можуть приймати будь-яке значення в певному діапазоні. Час і відстань безперервні; стать, оцінка SAT і «час округлений до найближчої секунди» не є. Змінні, які не є безперервними, відомі як дискретні змінні. Жодна виміряна змінна не є справді безперервною; однак дискретні змінні, виміряні з достатньою точністю, часто можна вважати безперервними для практичних цілей.
Корельовані пари t test/Пов'язані пари t test
Тест на різницю між засобами двох умов, коли є пари балів. Як правило, кожна пара балів з іншого предмета.
Врівноважений
Балансування - це метод уникнення плутанини між змінними. Розглянемо експеримент, в якому випробовувані перевіряються як на завдання часу слухової реакції (в якому суб'єкти реагують на слуховий подразник), так і завдання часу візуальної реакції (в якому суб'єкти реагують на зоровий подразник). Половині випробовуваних спочатку дається візуальне завдання, а іншій половині випробовуваних спочатку дається слухове завдання. Таким чином, немає плутанини порядку презентації та завдання.
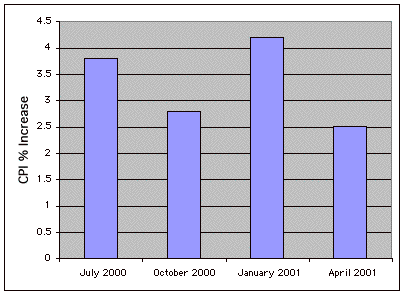
Індекс споживчих цін - ІСЦ
Також відомий як індекс вартості життя, ІСЦ - це фінансова статистика, яка вимірює зміну ціни представницької групи товарів з плином часу.
Змінна критерію
У регресійному аналізі (наприклад, лінійної регресії) змінною критерію є передбачувана змінна. Загалом, змінна критерію є залежна змінна.
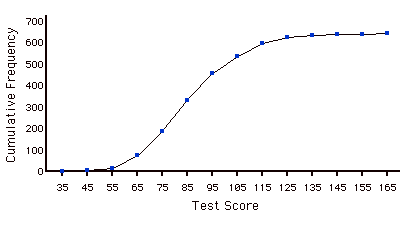
Сукупний розподіл частот
Розподіл, що показує кількість спостережень менше або дорівнює значенням на\(X\) -осі. Наступний графік показує сукупний розподіл балів за тестом.
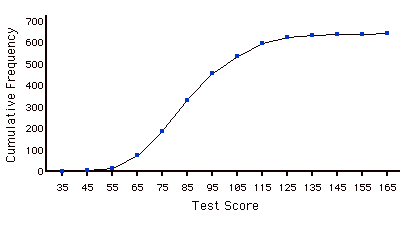
Накопичувальний багатокутник частоти
Частотний багатокутник, вершини якого представляють суму всіх попередніх частот класу даних. Наприклад, якщо багатокутник частоти мав вершини\(5, 8, 3, 7, 10\), багатокутник кумулятивної частоти на тих же даних матиме вершини\(5, 13, 16, 23, 33\). Як інший приклад, нижче наведено кумулятивний розподіл частот для балів на тесті з психології.
Дані
Сукупність значень, які будуть використовуватися для статистичного аналізу.
Залежна змінна
Змінна, яка вимірює експериментальний результат. У більшості експериментів спостерігається вплив незалежної змінної на залежні змінні. Наприклад, якщо дослідження досліджувало ефективність експериментального лікування депресії, то мірою депресії буде залежна змінна.
Синонім: залежна міра
Описова статистика
- Галузь статистики займається описом і узагальненням даних.
- Набір статистичних даних, таких як середнє значення, стандартне відхилення та перекіс, які описують розподіл.
Відхилення балів
Бали, які виражаються у вигляді відмінностей (відхилень) від якогось значення, зазвичай середні. Щоб перетворити дані в бали відхилення, як правило, означає відняти середній бал один від одного бал. Таким чином\(1\), значення\(2\), і\(3\) у формі відхилення оцінки будуть обчислюватися шляхом віднімання середнього значення\(2\) від кожного значення і буде\(-1, 0, 1\).
Ступені свободи - df
Ступінь свободи оцінки - це кількість незалежних фрагментів інформації, які йдуть в кошторис. В цілому ступені свободи для оцінки дорівнюють числу значень мінус кількість параметрів, оцінених на шляху до розглянутої кошторису. Наприклад, щоб оцінити дисперсію популяції, потрібно спочатку оцінити середнє значення чисельності населення. Тому, якщо оцінка дисперсії заснована на\(N\) спостереженнях, існують\(N - 1\) ступені свободи.
Дискретна змінна
Змінні, які можуть приймати лише кінцеве число значень, називаються «дискретними змінними». Всі якісні змінні дискретні. Деякі кількісні змінні дискретні, такі як продуктивність\(1\), оцінена як\(2\)\(3\),\(4\),, або\(5\), або температура округлена до найближчого ступеня. Іноді змінна, яка приймає достатньо дискретних значень, може вважатися безперервною для практичних цілей. Одним із прикладів є час до найближчої мілісекунди.
Змінні, які можуть приймати нескінченну кількість можливих значень, називаються «безперервними змінними».
Розподіл/Частотний розподіл
Розподіл емпіричних даних називається частотним розподілом і складається з підрахунку кількості входжень кожного значення. Якщо дані безперервні, то використовується згрупований частотний розподіл. Зазвичай розподіл зображується за допомогою частотного багатокутника або гістограми.
Математичні рівняння часто використовуються для визначення розподілів. Нормальний розподіл - це, мабуть, найвідоміший приклад. Багато емпіричних розподілів добре наближені математичними розподілами, такими як нормальний розподіл.
Очікувана вартість
Очікувана величина статистики - це середнє значення розподілу вибірки статистики. Це можна сміливо вважати довгостроковим середнім значенням статистики.
Фактор/ Незалежні змінні
Змінні, якими керує експериментатор, на відміну від залежних змінних. Більшість експериментів полягають у спостереженні впливу незалежної змінної (-ів) на залежну змінну (и).
Факторіальний дизайн
У факторіальному дизайні кожен рівень кожної незалежної змінної парний з кожним рівнем один одного незалежної змінної. Таким чином,\(2 \times 3\) факторіальний дизайн складається з\(6\) можливих комбінацій рівнів незалежних змінних.
Помилково позитивний
Хибне позитив виникає, коли діагностична процедура повертає позитивний результат, тоді як справжній стан суб'єкта негативний. Наприклад, якщо тест на стрептоп говорить, що у пацієнта стрептоп, коли насправді він або вона цього не робить, то помилка в діагностиці буде називатися хибнопозитивною. У деяких контекстах помилкове спрацювання називається помилковою тривогою. Поняття схоже на помилку типу I в тестуванні значущості.
Сімейний коефіцієнт помилок
Коли проводиться серія тестів на значущість, familywise rate помилок (\(FER\)) - це ймовірність того, що один або кілька тестів значущості призводять до помилки типу I.
Далеке значення
Однією з складових квадратного графіка, далекі значення є ті, які більше, ніж\(2\) кроки від найближчого шарніра. Вони знаходяться за межами зовнішніх огорож.
сприятливий результат
Успішним результатом є зацікавлений результат. Наприклад, можна визначити успішний результат у перевертанні монети як голови. Термін «успішний результат» не обов'язково означає, що результат бажаний — в деяких експериментах успішним результатом може стати невдача тесту, або виникнення небажаної події.
Частотний розподіл
Для дискретної змінної розподіл частоти складається з розподілу кількості входжень для кожного значення змінної. Для безперервної змінної це кількість входжень для різних діапазонів змінних.
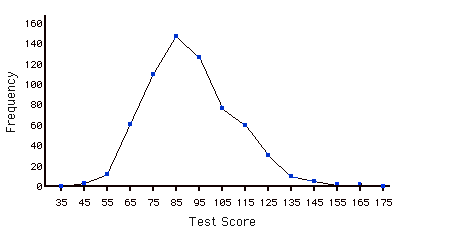
Багатокутник частоти
Частотний багатокутник - це графічне зображення розподілу. Він розділяє змінну на\(x\) -осі на різні суміжні класові інтервали (зазвичай) однакової ширини. Висоти точок багатокутника представляють частоти класу.
Таблиця частот
Таблиця, що містить кількість входжень у кожному класі даних; наприклад, кількість кожного кольору M&Ms у мішку. Таблиці частот часто використовуються для створення гістограм і частотних багатокутників. Коли для кількісної змінної створюється таблиця частот, зазвичай використовується згрупована таблиця частот.
Згрупована таблиця частот
Згрупована таблиця частот показує кількість значень для різних діапазонів балів. Нижче показана згрупована таблиця частот для часу відгуку (у мілісекундах) для простого рухового завдання.
| Діапазон | Частота |
| 500-600 | 3 |
| 600-700 | 6 |
| 700-800 | 5 |
| 800-900 | 5 |
| 900-1000 | 0 |
| 1000-1100 | 1 |
Середнє геометричне
Середнє геометричне - міра центральної тенденції. Середнє геометричне з n чисел виходить шляхом множення всіх їх разом, а потім взяття\(n^{th}\) кореня з них. Наприклад, для чисел\(1\), і\(10\)\(100\), добутком всіх чисел є:\(1 \times 10 \times 100 = 1,000\). Так як чисел три, то беремо кубоподібний корінь продукту (\(1,000\)), який дорівнює\(10\).
Графіки/Графіка
Графіки часто є найефективнішим способом опису розподілів та взаємозв'язків між змінними. Серед найбільш поширених графіків є гістограми, коробчасті графіки, гістограми та розсіювачі.
Згрупований розподіл частот
Згрупований розподіл частот - це розподіл частот, в якому частоти відображаються для діапазонів даних, а не для окремих значень. Наприклад, розподіл висот може бути розрахований шляхом визначення діапазонів в один дюйм. Частота особин з різною висотою, округлена до найближчого дюйма, потім буде таблична.
Гармонічне середнє
Середнє гармонійне n чисел (\(X_1\)to\(X_n\)) обчислюється за такою формулою:
\[\mathit{Harmonic\; Mean} = \frac{n}{\tfrac{1}{x_1}+\tfrac{1}{x_2}+\cdots +\tfrac{1}{x_n}}\]
Часто обчислюється гармонійне середнє значення розмірів вибірки.
Гістограма
Гістограма - це графічне зображення розподілу. Він розділяє змінну на\(x\) -осі на різні суміжні класові інтервали (зазвичай) однакової ширини. Висоти смуг представляють частоти класу.
Історія Ефект
Проблема плутанини, де плин часу, а не змінна інтересу, відповідає за спостережувані ефекти.
однорідність дисперсії
Припущення, що дисперсії всіх популяцій рівні.
Гомошоподібність
У лінійній регресії передбачається припущення, що дисперсія навколо лінії регресії однакова для всіх значень змінної предиктора.
Н-спред
Однією з складових ділянки коробки,\(H\) -spread є різниця між верхнім шарніром і нижнім шарніром.
iMac
Лінійка комп'ютерів, випущених Apple в\(1998\), яка намагалася зробити комп'ютери як більш доступними (більша простота використання), так і модними (вони вийшли в лінійці дизайнерських кольорів.)
Незалежність
Дві змінні вважаються незалежними, якщо значення однієї змінної не надає інформації про значення іншої змінної. Ці дві змінні були б некорельовані так, що р Пірсона буде\(0\).
Дві події є незалежними, якщо ймовірність виникнення другої події однакова незалежно від того, відбулася перша подія чи ні.
Незалежні заходи
Події\(A\) і\(B\) є незалежними подіями, якщо ймовірність події\(B\) відбувається однакова незалежно від того,\(A\) відбувається подія чи ні. Наприклад, якщо ви кидаєте два кубика, ймовірність того, що з'явиться другий кубик,\(1\) не залежить від того, чи підійшов перший кубик\(1\). Формально це можна констатувати з точки зору умовних ймовірностей:
\[P(A|B) = P(A)\\ P(B|A) = P(B)\]
умовивід
Акт про складання висновків про сукупність з вибірки.
Статистика інференційних
Галузь статистики займалася тим, щоб зробити висновки про сукупність з вибірки. Зазвичай це робиться шляхом випадкової вибірки, після чого йдуть висновки про центральну тенденцію або будь-який з ряду інших аспектів розподілу.
Вплив
Вплив відноситься до ступеня, в якій єдине спостереження в регресії впливає на оцінку параметрів регресії. Часто вимірюється термінами, наскільки прогнозовані бали для інших спостережень відрізнялися б, якби розглянуте спостереження не було включено.
Внутрішній паркан
На ділянці коробки нижня внутрішня огорожа знаходиться на одну сходинку нижче нижньої петлі, тоді як верхня внутрішня огорожа на одну сходинку вище верхньої петлі.
Взаємодія
Дві незалежні змінні взаємодіють, якщо ефект однієї зі змінних відрізняється в залежності від рівня іншої змінної.
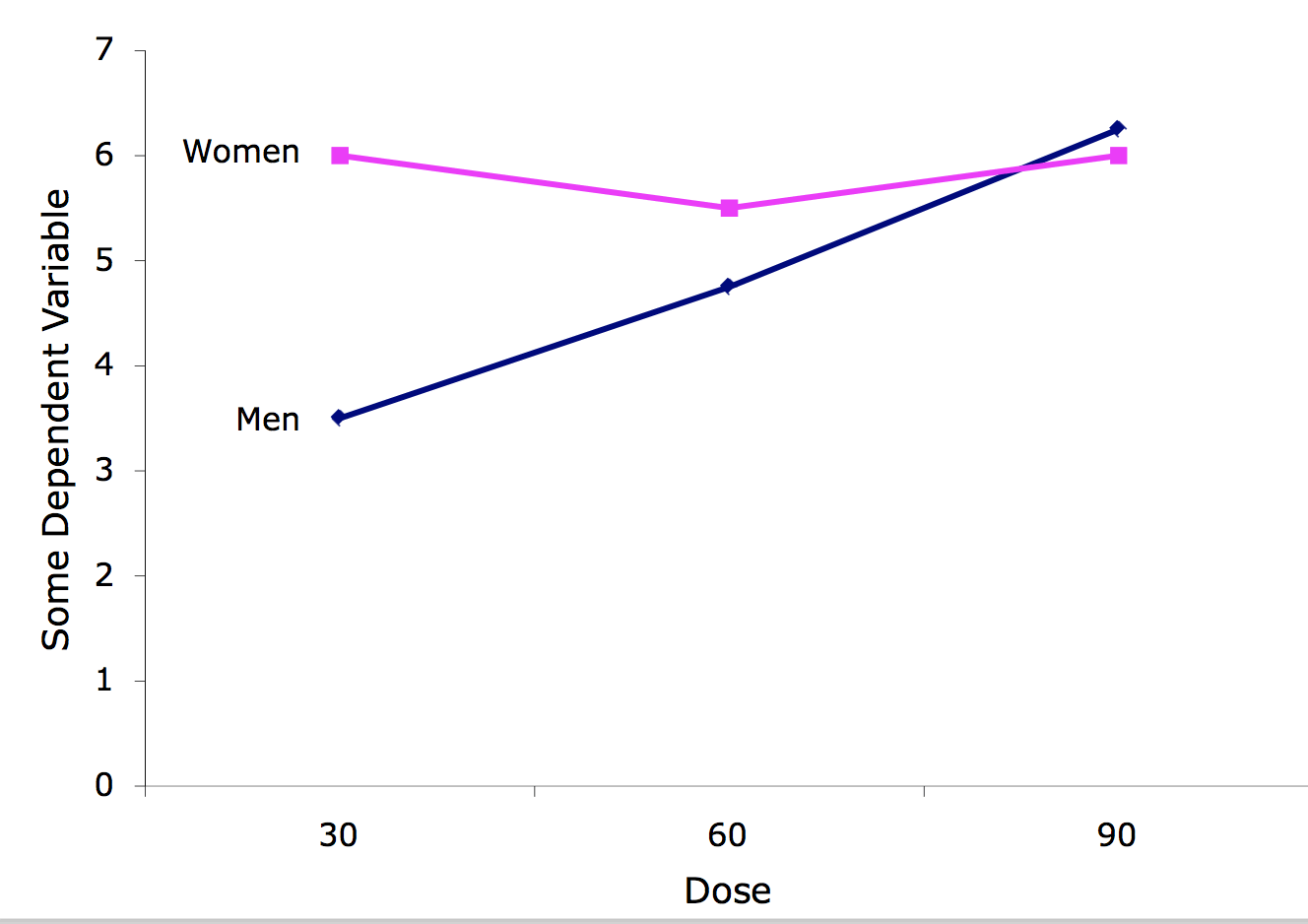
Ділянка взаємодії
Графік взаємодії відображає рівні однієї змінної на\(X\) осі і має окремий рядок для середніх кожного рівня іншої змінної. \(Y\)Вісь - залежна змінна. Погляд на цей графік показує, що ефект дозування відрізняється для чоловіків, ніж для жінок.
Міжквартильний діапазон
Інтерквартильний діапазон (\(IQR\)) - це (\(75^{th}\)процентиль —\(25^{th}\) процентиль). Це надійна міра мінливості.
Інтервальна оцінка
Інтервальна оцінка - це діапазон балів, які, ймовірно, містять оцінюваний параметр.
Інтервальні ваги
Один з\(4\) рівнів вимірювання, інтервальні шкали - це числові шкали, в яких інтервали мають однакову інтерпретацію. Як приклад розглянемо шкалу температури за Фаренгейтом. Різниця між\(30\) градусами і\(40\) градусами являє собою ту ж різницю температур, що і різниця між\(80\) градусами і\(90\) градусами. Це пояснюється тим, що кожен\(10\) градусний інтервал має однаковий фізичний сенс (з точки зору кінетичної енергії). На відміну від шкал співвідношення, інтервальні шкали не мають справжньої нульової точки.
тремтіння
Коли точки на графіку тремтяться, вони переміщуються горизонтально так, що всі точки можна побачити, а жодна з них не прихована через значення, що перекриваються. Приклад наведено нижче:
Куртоз
Куртоз вимірює, наскільки жирні або тонкі хвости розподілу відносно нормального розподілу. Його зазвичай визначають як:
\[\sum \frac{(X-\mu )^4}{\sigma ^4} - 3\]
Розподіли з довгими хвостами називаються лептокуртіческімі; розподіли з короткими хвостами називаються платикуртіческіе. Нормальні розподіли мають нульовий куртоз.
Лептокуртський
Розподіл з довгими хвостами щодо нормального розподілу - лептокуртіческій.
Рівень/Рівень змінної/Рівень множника
Коли фактор складається з різних умов лікування, кожен стан лікування вважається рівнем цього фактора. Наприклад, якби фактором була дозування препарату, і три дози були перевірені, то кожна доза була б одним рівнем фактора і фактор мав би три рівні.
Рівні вимірювання
Шкали вимірювань відрізняються за рівнем вимірювання. Існує чотири загальних рівня вимірювання:
- Номінальні ваги - це тільки етикетки.
- Порядкові ваги впорядковані, але не є справді кількісними. Рівні інтервали за порядковою шкалою не передбачають рівних інтервалів за основною ознакою.
- Інтервальні шкали впорядковані і рівні інтервали рівні інтервали на базовій ознаці. Однак інтервальні шкали не мають справжньої нульової точки.
- Шкали співвідношення - це інтервальні шкали, які мають справжню нульову точку. З масштабами співвідношення розумно говорити про те, що одне значення вдвічі більше іншого, наприклад.
кредитне плече
Кредитне плече - це фактор, що впливає на вплив спостереження в регресії. Кредитне плече базується на тому, наскільки значення спостереження на змінній предиктора відрізняється від середнього значення змінної предиктора. Чим більше важелі спостереження, тим більше потенціалу воно має бути впливовим спостереженням.
Фактор життя
Багато проблем може виникнути, коли вигадливі графіки використовуються над звичайними. Спотворення можуть виникати, коли висота об'єктів використовується для позначення значення, оскільки більшість людей звернуть увагу на області об'єктів, а не на їх висоту. Коефіцієнт брехні - це відношення ефекту, видимого на графіку, до фактичного ефекту в даних; якщо він відхиляється більше, ніж\(0.05\) від\(1\), графік, як правило, неприпустимий. Коефіцієнт брехні на наступному графіку майже\(6\).
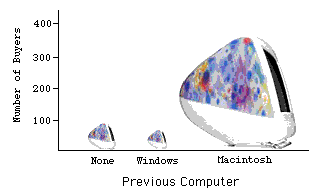
Брехня
Існує три види брехні:
- регулярна брехня
- проклята брехня
- статистика
Це за словами Бенджаміна Дізраелі, як цитує Марк Твен.
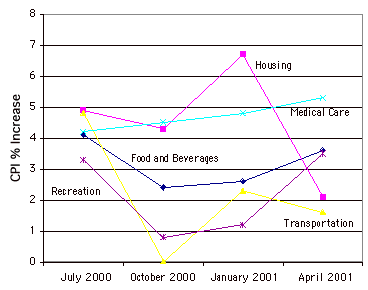
Лінійний графік
По суті гістограма, в якій висота кожного пар представлена однією точкою, причому кожна з цих точок з'єднана лінією. Лінійні графіки найкраще використовувати для відображення змін з часом, і ніколи не слід використовувати, якщо ваша\(X\) -вісь не є впорядкованою змінною. Приклад наведено нижче.
Лінійна комбінація
Лінійна комбінація змінних - це спосіб створення нової змінної шляхом об'єднання інших змінних. Лінійна комбінація - це та, в якій кожна змінна множиться на коефіцієнт і підсумовуються добуток. Наприклад, якщо
\[Y = 3X_1 + 2X_2 + 0.5X_3\]
\(Y\)то лінійна комбінація змінних\(X_1\)\(X_2\), і\(X_3\).
Лінійна регресія
Лінійна регресія - це метод прогнозування змінної критерію з однієї або декількох змінних предиктора. У простій регресії критерій прогнозується з однієї змінної предиктора, а найкраща пряма лінія має вигляд:
\[Y' = bX + A\]
де\(Y'\) передбачена оцінка,\(X\) - змінна предиктора\(b\), нахил, і\(A\)\(Y\) перехоплення. Як правило, критерієм для лінії «найкраща підгонка» є лінія, для якої сума квадратних похибок прогнозування зведена до мінімуму. При множинній регресії критерій прогнозується з двох або більше змінних предиктора.
Лінійний зв'язок
Існує ідеальна лінійна залежність між двома змінними, якщо розсіювач точок падає на пряму лінію. Відносини є лінійними, навіть якщо точки розходяться від лінії до тих пір, поки розбіжність є випадковою, а не є систематичною.
Лінійне перетворення
Лінійне перетворення - це будь-яке перетворення змінної, яке може бути досягнуто шляхом множення її на константу, а потім додавання другої константи. Якщо\(Y\) це перетворене значення\(X\), то\(Y = aX + b\). Перетворення з градусів Фаренгейта в градуси Цельсія є лінійним і здійснюється за формулою:
\[C = 0.55556F - 17.7778\]
Логарифм - Log
Логарифм числа - це ступінь, до якої повинна бути піднята основа логарифма, щоб дорівнювати числу. Якщо основа логарифма є,\(10\) а число є,\(1,000\) то журнал\(3\) так як\(10\) повинен бути піднятий на\(3^{rd}\) ступінь рівний\(1,000\).
Нижнє суміжне значення
Компонент квадратної ділянки, нижнє суміжне значення є найменшим значенням у даних над внутрішнім нижнім парканом.
Нижній шарнір
Компонент графіка коробки, нижній шарнір - це\(25^{th}\) процентиль. Верхній шарнір -\(75^{th}\) процентиль.
М & М
Вид цукерок, що складається з шоколаду всередині оболонки. M & M випускаються в різних кольорах.
Основний ефект
Основним ефектом незалежної змінної є ефект усереднення змінної по всіх рівнях іншої змінної (-ів). Наприклад, у дизайні з віком та статтю як факторами основним ефектом статі буде різниця між усередненими статями у всіх віках, що використовуються в експерименті.
Похибка
Коли статистика використовується для оцінки параметра, зазвичай обчислюється довірчий інтервал. Похибка - це різниця між статистикою та кінцевими точками інтервалу. Наприклад, якби статистика була\(0.6\) і довірчий інтервал\(0.4\) коливався від до\(0.8\), то похибка була б\(0.20\). Якщо не вказано інше, використовується\(95\%\) довірчий інтервал.
Середнє граничне
У дизайні з двома факторами граничні засоби для одного фактора є засобом для цього фактора, усередненого на всіх рівнях іншого фактора. У таблиці, наведеній нижче, двома факторами є «Відносини» та «Вага супутника». Граничні засоби для кожного з двох рівнів Відносини (подруга і знайомство) обчислюються шляхом усереднення на двох рівнях ваги супутника. Таким чином, граничне середнє для Знайомства\(6.37\) - це середнє значення\(6.15\) і\(6.59\).
|
Вага компаньйона
|
||||
|
|
ожиріння
|
Типові
|
граничне середнє значення
|
|
| Відносини |
подруга
|
5.65
|
6.19
|
5.92
|
|
Знайомство
|
6.15
|
6.59
|
6.37
|
|
|
граничне середнє значення
|
5.90
|
6.39
|
||
Середнє/ Середнє арифметичне
Також відомий як середнє арифметичне, середнє, як правило, те, що мається на увазі під словом «середнє». Середнє значення є, мабуть, найпоширенішою мірою центральної тенденції. Середнє значення змінної задається (сума всіх її значень)/(кількість значень). Наприклад, середнє значення\(4\)\(8\), і\(9\) є\(7\). Зразок середнього пишеться як M, а населення означає як грецька буква mu (\(μ\)). Незважаючи на свою популярність, середнє значення може не бути відповідною мірою центральної тенденції для перекосованих розподілів або в ситуаціях з викидами.
Медіана
Медіана - популярна міра центральної тенденції. Це\(50^{th}\) процентиль розподілу. Щоб знайти медіану ряду значень, спочатку впорядкуйте їх, потім знайдіть спостереження посередині: медіана\(5, 2, 7, 9, 4\) is\(5\). (Зауважте, що якщо є парна кількість значень, то береться середнє значення двох середніх: медіана\(4, 6, 8,10\) є\(7\).) Медіана часто є більш доречною, ніж середнє в перекосованих розподілах і в ситуаціях з викидами.
Міс
Промахи виникають, коли діагностичний тест повертає негативний результат, але справжній стан обстежуваного позитивний. Наприклад, якщо у людини стрептоглотка і діагностичний тест не вказує на це, значить, стався промах. Поняття схоже на помилку типу II в тестуванні значущості.
Режим
Режим є мірою центральної тенденції. Це найчастіше значення в розподілі: режим\(3, 4, 4, 5, 5, 5, 8\) є\(5\). Зверніть увагу, що режим може сильно відрізнятися від середнього і медіани.
множинна регресія
Множинна регресія - це лінійна регресія, в якій для прогнозування критерію використовуються дві або більше змінних предиктора.
Негативна асоціація
Існує негативна асоціація між змінними\(X\) і\(Y\) якщо менші значення\(X\) пов'язані з більшими значеннями\(Y\) і більшими значеннями\(X\) пов'язані з меншими значеннями\(Y\).
Номінальна шкала
Номінальна шкала - це один з чотирьох часто використовуваних рівнів вимірювання. Ніякого впорядкування не мається на увазі, а додавання/віднімання та множення/ділення буде недоречним для змінної за номінальною шкалою. {Жіночий, Чоловічий} та {Буддійський, Християнський, Індуїстський, Мусульманин} не мають природного впорядкування (крім алфавітного). Іноді числові значення є номінальними: наприклад, якщо змінна була закодована як\(\text{Female = 1, Male = 2}\), множина\({1,2}\) залишається номінальною.
Не представник
Нерепрезентативна вибірка - це вибірка, яка не точно відображає чисельність населення.
Нормальний розподіл
Один з найпоширеніших неперервних розподілів, нормальний розподіл іноді називають «дзвоноподібним розподілом». Якщо\(μ\) середнє розподіл, а\(σ\) стандартне відхилення, то висота (ординат) нормальний розподіл задається
\[\frac{1}{\sqrt{2\pi \sigma ^2}}e^{\tfrac{-(x-\mu )^2}{2\sigma ^2}}\]
Графік нормального розподілу із середнім значенням\(50\) і стандартним відхиленням\(10\) показаний нижче.
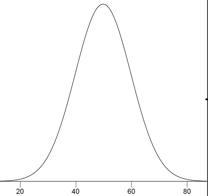
Якщо середнє значення є,\(0\) а стандартне відхилення є\(1\), розподіл називається «стандартним нормальним розподілом».
Нульова гіпотеза
Нульова гіпотеза - це гіпотеза, перевірена на значущість тестування Як правило, гіпотеза про те, що параметр дорівнює нулю або що різниця між параметрами дорівнює нулю. Наприклад, нульова гіпотеза може полягати в тому, що різниця між засобами населення дорівнює нулю. Експериментатори зазвичай розробляють експерименти, щоб дозволити відхилити нульову гіпотезу.
Нульова гіпотеза Омнінуса
Нульова гіпотеза про те, що всі засоби населення рівні.
Однохвостий тест /Однохвоста ймовірність/Спрямований тест
Останній крок тестування значущості передбачає обчислення ймовірності того, що статистика буде відрізнятися настільки ж або більше від параметра, зазначеного в нульовій гіпотезі, як і статистика, отримана в експерименті.
Імовірність, обчислена з урахуванням відмінностей лише в одному напрямку, наприклад, статистика більша за параметр, називається однохвостою ймовірністю. Наприклад, якщо параметр є,\(0\) а статистика є\(12\), однохвоста ймовірність (позитивний хвіст) буде ймовірністю статистичної істоти\(≥12\). Порівняйте з двоххвостою ймовірністю, яка буде ймовірністю бути\(≤ -12\) або\(≥12\).
Порядкова шкала
Один з чотирьох часто використовуваних рівнів вимірювання, порядкова шкала - це набір впорядкованих значень. Однак встановленої відстані між значеннями шкали немає. Наприклад, для шкали: (Дуже бідний, Поганий, Середній, Хороший, Дуже хороший) - порядкова шкала. Ви можете призначити числові значення за порядковою шкалою: оцінка ефективності, наприклад,\(1\) для «Дуже бідних»,\(2\) для «Бідних» і т.д., але немає впевненості, що різниця між балом\(1\) і\(2\) означає те ж саме, що і різниця між балом\(2\) і \(3\).
Ортогональні порівняння
Коли порівняння між засобами дають абсолютно незалежну інформацію, порівняння називаються «ортогональними». Якби експеримент з чотирма групами проводився, то порівняння\(\text{Groups 1 and 2}\) було б ортогональним до порівняння,\(\text{Groups 3 and 4}\) оскільки немає нічого в порівнянні\(\text{Groups 1 and 2}\), що дає інформацію про порівняння\(\text{Groups 3 and 4}\).
Зовнішній паркан
На ділянці коробки нижня зовнішня огорожа - це\(2\) ступені нижче нижньої петлі, тоді як верхня внутрішня огорожа - це\(2\) сходинки над верхнім шарніром.
викиди
Випадки - це нетипові, нечасті спостереження; значення, які мають крайнє відхилення від центру розподілу. Не існує універсально узгодженого критерію визначення викидів, і викиди слід відкидати лише з особливою обережністю. Однак завжди слід оцінювати вплив викидів на статистичні висновки.
Зовнішнє значення
Компонент графіка коробки, зовнішні значення більше, ніж\(1\) крок за найближчий шарнір. Вони знаходяться поза внутрішнім парканом, але не за зовнішнім парканом.
Попарні порівняння
Попарні порівняння - це порівняння між парами засобів.
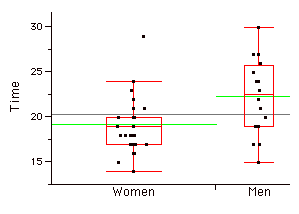
Паралельні ділянки коробки
Два або більше графіків коробки намальовані на одній\(Y\) -осі. Вони часто корисні для порівняння можливостей дистрибутивів. Приклад, що зображує часи, коли брали зразки жінок і чоловіків для виконання завдання, наведено нижче.
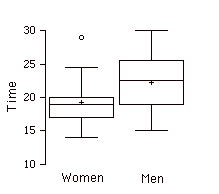
Параметр
Значення, розраховане в популяції. Наприклад, значення середнього числа в популяції є параметром. Порівняйте зі статистикою, яка є значенням, обчисленим у вибірці для оцінки параметра.
Частковий ухил
Частковий нахил у множинній регресії - це нахил зв'язку між змінною предиктора, яка не залежить від інших змінних предиктора та критерію. Це також коефіцієнт регресії для відповідної змінної предиктора.
\(r\)Пірсона/Кореляція моменту продукту Пірсона/Кореляція Пірсона
Кореляція Пірсона є мірою сили лінійної залежності між двома змінними. Це варіюється від\(-1\) ідеального негативного ставлення до\(+1\) ідеальних позитивних відносин. Кореляція\(0\) означає, що немає лінійної залежності.
Процентиль
Загальновизнаного визначення процентиля не існує. Використовуючи\(65^{th}\) процентиль як приклад, деякі статистики визначають\(65^{th}\) процентиль як найнижчий бал, який більший\(65\%\) за бали. Інші визначили\(65^{th}\) процентиль як найнижчий бал, який більше або дорівнює\(65\%\) балів. Більш складне визначення наведено нижче. Першим кроком є обчислення рангу (\(R\)) відповідного процентиля. Робиться це за наступною формулою:
\[R = \frac{P}{100} \times (N + 1)\]
де\(P\) - шуканий процентиль і\(N\) - кількість чисел. Якщо\(R\) ціле число, то\(P^{th}\) процентиль - це число з рангом\(R\). Коли\(R\) не ціле число, обчислюємо\(P^{th}\) процентиль шляхом інтерполяції наступним чином:
- Визначте\(IR\) як цілу частину\(R\) (число ліворуч від десяткової крапки).
- Визначте\(FR\) як дробову частину або\(R\).
- Знайти оцінки з рангом\(IR\) і з рангом\(IR + 1\).
- Інтерполяція шляхом множення різниці між балами на\(FR\) і додайте результат до нижнього балу.
Коефіцієнт помилок порівняння
Частота помилок порівняння відноситься до частоти помилок типу I будь-якого тесту значущості, проведеного в рамках серії тестів на значущість. Таким чином, якби тести\(10\)\(0.05\) значущості проводилися на рівні значущості, то коефіцієнт помилок для порівняння був би\(0.05\). Порівняйте з сімейною частотою помилок.
Кругова діаграма
Графічне представлення даних, кругова діаграма показує відносні частоти класів даних. Це коло, розрізаний на кілька клинів, по одному для кожного класу, з площею кожного клина пропорційною його відносній частоті. Кругові діаграми ефективні лише для невеликої кількості класів і є одним з менш ефективних графічних уявлень.
Плацебо
Пристрій, що використовується в клінічних випробуваннях, плацебо візуально не відрізняється від досліджуваного медикаменту, але в дійсності не має ніякого лікувального ефекту (найчастіше, цукрова пігулка). Група суб'єктів, обраних випадковим чином, приймає плацебо, інші приймають той чи інший вид ліків. Це робиться для запобігання плутанини медико-психологічного впливу препарату. Навіть цукрова таблетка може призвести до того, що деякі пацієнти повідомляють про поліпшення та побічні ефекти.
Планове порівняння/апріорне порівняння
Порівняння, яке планується перед проведенням експерименту або принаймні до вивчення даних. Також називається апріорним порівнянням.
Платикуртік
Розподіл з короткими хвостами щодо нормального розподілу - платікуртіческій.
Оцінка точки
Коли параметр оцінюється, оцінка може бути як єдиним числом, так і діапазоном чисел, наприклад, у довірчому інтервалі. Коли кошторис являє собою єдине число, кошторис називається «точковою оцінкою».
Поліноміальна регресія
Поліноміальна регресія - це форма множинної регресії, в якій використовуються повноваження змінної предиктора замість інших змінних предиктора. У наступному прикладі критерій (\(Y\)) передбачається\(X\),\(X^2\) і,\(X^3\).
\[Y = b_1X + b_2X^2 + b_3X^3 + A\]
Чисельність населення
Популяція - це повний набір спостережень, який цікавить дослідника. Зіставте це з вибіркою, яка є підмножиною популяції. Сукупність може бути визначена зручним для дослідника способом. Наприклад, можна визначити населення, як і всі дівчата четвертого класу в Х'юстоні, штат Техас. Або інша популяція - це набір всіх дівчат четвертого класу в США. Вихідні статистичні дані обчислюються з вибіркових даних для того, щоб зробити висновки про сукупність.
Позитивна асоціація
Існує позитивна асоціація між змінними,\(X\) і\(Y\) якщо менші значення\(X\) пов'язані з меншими значеннями\(Y\) і більшими значеннями\(X\) пов'язані з більшими значеннями\(Y\).
Задня ймовірність
Задня ймовірність події - це ймовірність події, обчисленої після збору нових даних. Починається з попередньої ймовірності події і переглядає її з урахуванням нових даних. Наприклад, якщо\(0.01\) населення має шизофренію, то ймовірність того, що людина, намальована навмання, матиме шизофренію\(0.01\). Це попередня ймовірність. Якщо ви потім дізнаєтеся, що їх оцінка на тест особистості свідчить про те, що людина є шизофреніком, ви б відповідно відрегулювали свою ймовірність. Скоригована ймовірність - це задня ймовірність.
Потужність
У тестуванні значущості влада - це ймовірність відхилення помилкової нульової гіпотези.
Точність
Точність статистики стосується того, наскільки близько вона, як очікується, буде до параметра, який він оцінює. Точна статистика менше відрізняється від вибірки до вибірки. Точність статистики зазвичай визначається з точки зору її стандартної помилки.
Змінна предиктора
Змінна предиктора - це змінна, яка використовується в регресії для прогнозування іншої змінної. Іноді його називають незалежною змінною, якщо вона маніпулюється, а не просто вимірюється.
Попередня ймовірність
Попередня ймовірність події - це ймовірність події, обчисленої до збору нових даних. Починається з попередньої ймовірності події і переглядає її з урахуванням нових даних. Наприклад, якщо\(0.01\) населення має шизофренію, то ймовірність того, що людина, намальована навмання, матиме шизофренію\(0.01\). Це попередня ймовірність. Якщо ви потім дізнаєтеся, що там оцінка на тест особистості свідчить про те, що людина є шизофреніком, ви б відповідно відрегулювали свою ймовірність. Скоригована ймовірність - це задня ймовірність.
Функція щільності ймовірності
Для дискретної випадкової величини розподіл ймовірностей містить ймовірність кожного можливого результату. Однак для неперервної випадкової величини ймовірність будь-якого одного результату дорівнює нулю (якщо вказати для неї достатню кількість десяткових знаків). Функція щільності ймовірності - це формула, яка може бути використана для обчислення ймовірностей діапазону результатів для неперервної випадкової величини. Сума всіх щільностей завжди\(1.0\) і значення функції завжди більше або дорівнює нулю.
Розподіл ймовірностей
Для дискретної випадкової величини розподіл ймовірностей містить ймовірність кожного можливого результату. Сума всіх ймовірностей завжди\(1.0\).
Значення\(p\) ймовірності/значення
У тестуванні значущості значення ймовірності (іноді його називають\(p\) значенням) - це ймовірність отримання статистики, відмінної або більш відмінної від параметра, зазначеного в нульовій гіпотезі як статистика, отримана в експерименті. Значення ймовірності обчислюється за умови, що нульова гіпотеза істинна. Чим нижче значення ймовірності, тим сильніше докази того, що нульова гіпотеза помилкова. Традиційно нульова гіпотеза відхиляється, якщо значення ймовірності нижче\(0.05\).
Значення ймовірності можуть бути як один хвостатий, так і двоххвостий.
Якісні змінні/Категорична змінна
Також відомі як категоріальні змінні, якісні змінні - це змінні, які не мають природного почуття впорядкування. Тому вони вимірюються за номінальною шкалою. Наприклад, колір волосся (Чорний, Коричневий, Сірий, Червоний, Жовтий) є якісною змінною, як це називають (Адам, Беккі, Крістіна, Дейв.). Якісні змінні можуть бути закодовані так, щоб вони виглядали числовими, але їх числа безглузді, як в\(\text{male=1, female=2}\). Змінні, які не є якісними, відомі як кількісні змінні.
Кількісна змінна
Змінні, які вимірюються за числовою або кількісною шкалою. Порядкові, інтервальні і коефіцієнтні шкали кількісні. Населення країни, розмір взуття людини або швидкість автомобіля - це все кількісні змінні. Змінні, які не є кількісними, відомі як якісні змінні.
Випадкове призначення
Випадкове присвоєння відбувається, коли суб'єкти в експерименті випадковим чином присвоюються умовам. Випадкове призначення запобігає систематичному плутанню ефектів лікування з іншими змінними.
Випадкова вибірка/проста випадкова вибірка
Процес вибору підмножини сукупності для цілей статистичного висновку. Випадкова вибірка означає, що кожен член населення однаково імовірно буде обраний.
Діапазон
Різниця між максимальним і мінімальним значеннями змінної або розподілу. Діапазон - найпростіша міра мінливості.
Шкала співвідношення
Один з чотирьох основних рівнів вимірювання, шкала співвідношення - це числова шкала з істинною нульовою точкою і в якій заданий інтервал розмірів має однакову інтерпретацію для всієї шкали. Вага - це шкала співвідношення, Тому має сенс сказати, що\(200\) фунт людина важить вдвічі більше, ніж\(100\) фунт людини.
Регресія
Регресія означає «передбачення». Регресія\(Y\) on\(X\) означає передбачення\(Y\) по\(X\).
Коефіцієнт регресії
Коефіцієнт регресії - це нахил лінії регресії в простій регресії або частковий нахил при множинній регресії.
Лінія регресії
У лінійній регресії лінія найкращого прилягання називається лінією регресії.
відносна частота
Частка спостережень, що потрапляють в даний клас. Наприклад, якщо мішок\(55\) M & M має\(11\) зелений M & M, то частота зелених M & M є\(11\) і відносна частота дорівнює\(11/55 = 0.20\). Відносні частоти часто використовуються в гістограмах, кругових діаграмах та гістограмах.
Відносний розподіл частот
Відносний розподіл частот подібно до розподілу частот, за винятком того, що він складається з пропорцій входжень замість чисел входжень для кожного значення (або діапазону значень) змінної.
Надійність
Хоча існує багато способів уявлення про надійність тесту, класичний спосіб полягає у визначенні надійності як кореляції між двома паралельними формами тесту. Якщо визначено таким чином, надійність - це відношення істинної дисперсії балів до дисперсії тестових балів. Хронбаха\(α\) є загальною мірою надійності.
Коефіцієнт повторюваних заходів/Повторювані заходи Змінна/Всередині суб'єктів Фактор/Всередині суб'єктів змінна
Змінна всередині суб'єктів - це незалежна змінна, яка маніпулюється шляхом тестування кожного предмета на кожному рівні змінної. Порівняйте з змінною між суб'єктами, в якій для кожного рівня змінної використовуються різні групи суб'єктів.
Представницький зразок
Репрезентативна вибірка - це вибірка, обрана відповідно до якостей популяції, з якої вона отримана. При великому розмірі вибірки випадкова вибірка наближається до репрезентативної вибірки; стратифікована випадкова вибірка може бути використана, щоб зробити невеликий зразок більш репрезентативним
Міцний
Щось міцне, якщо воно добре тримається перед лицем негараздів. Міра центральної тенденції або мінливості вважається надійною, якщо на неї не сильно впливають кілька екстремальних балів. Статистичний тест вважається надійним, якщо він працює добре, незважаючи на помірні порушення припущень, на яких він базується.
Зразок
Вибірка - це підмножина сукупності, часто береться з метою статистичного висновку. Як правило, використовується випадкова вибірка.
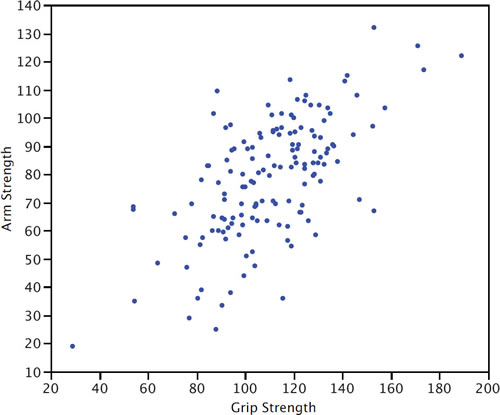
Розкид ділянки
Графік розкиду двох змінних показує значення однієї змінної на\(Y\) осі і значення іншої змінної на\(X\) осі. Графіки розкиду добре підходять для виявлення взаємозв'язку між двома змінними. Графік розкиду, показаний нижче, ілюструє взаємозв'язок між силою зчеплення та силою руки у вибірці робітників.
Напів-інтерквартильний діапазон
Напівквартильний діапазон - це інтерквартильний діапазон, розділений на\(2\). Це надійна міра мінливості. Інтерквартильний діапазон - це (\(75^{th}\)процентиль\(–\)\(25^{th}\) процентиль).
Рівень значущості/A рівень
У тестуванні значущості рівень значущості є найвищим значенням значення ймовірності, для якого нульова гіпотеза відхиляється. Загальними рівнями значущості є\(0.05\) і\(0.01\). Якщо використовується\(0.05\) рівень, то нульова гіпотеза відхиляється, якщо значення ймовірності менше або дорівнює\(0.05\).
Тестування значущості/Тестування гіпотез/Значна різниця
Статистична процедура, яка перевіряє життєздатність нульової гіпотези. Якщо дані (або більш екстремальні дані) дуже малоймовірні, враховуючи, що нульова гіпотеза вірна, то нульова гіпотеза відхиляється. Якщо дані або більш екстремальні дані не малоймовірні, то нульова гіпотеза не відхиляється. Якщо нульова гіпотеза відхилена, то результат тесту вважається значним. Статистично значущий ефект не означає, що ефект важливий.
Простий ефект
Проста дія фактора - це вплив цього фактора на одному рівні іншого фактора. Наприклад, у дизайні з віком та статтю як факторами вплив віку для жінок був би одним із простих ефектів віку.
Проста регресія
Проста регресія - це лінійна регресія, в якій для прогнозування критерію використовується ще одна змінна предиктора.
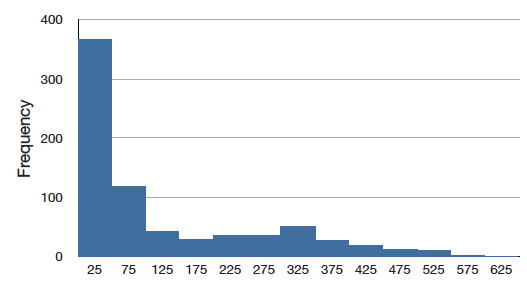
Перекіс
Розподіл перекошується, якщо один хвіст виходить далі іншого. Розподіл має позитивний перекіс (перекіс вправо), якщо хвіст праворуч довший. Див. Графік нижче для прикладу.
Розподіл має негативний перекіс (перекіс вліво), якщо хвіст зліва довший. Див. Графік нижче для прикладу.
Ухил
Нахил лінії - це зміна\(Y\) для кожної зміни однієї одиниці\(X\). Іноді його визначають як «підйом над бігом», що є одним і тим же. Нахил чорної лінії на графіку полягає в\(0.425\) тому, що лінія збільшується\(0.425\) з кожним разом\(X\) збільшується на\(1.0\).
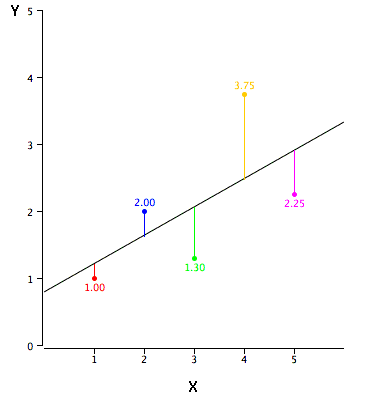
Відхилення у квадраті
Квадратне відхилення - це різниця між двома значеннями в квадраті. Число, яке мінімізує суму квадратних відхилень для змінної, є її середнім.
Стандартне відхилення
Стандартне відхилення - широко використовувана міра мінливості. Він обчислюється, взявши квадратний корінь дисперсії. Важливим атрибутом стандартного відхилення як міри мінливості є те, що якщо відомі середнє і стандартне відхилення нормального розподілу, можна обчислити ранг процентиля, пов'язаний з будь-яким заданим балом.
Стандартна помилка
Стандартна похибка статистики - це стандартне відхилення розподілу вибірки цієї статистики. Наприклад, стандартна похибка середнього - це стандартне відхилення розподілу вибірки середнього. Стандартні помилки відіграють вирішальну роль у побудові довірчих інтервалів та тестування значущості.
Стандартна похибка вимірювання
У теорії випробувань стандартна похибка вимірювання - це стандартне відхилення спостережуваних тестових балів для заданої істинної оцінки. Зазвичай оцінюється за наступною формулою, в якій\(s\) є стандартне відхилення тестових балів і\(r\) є надійністю тесту.
\[S_{measurement} = s\sqrt{1-r}\]
Стандартна похибка середнього
Стандартна похибка середнього - це стандартне відхилення розподілу вибірки середнього. Формула стандартної похибки середнього значення в популяції така:
\[\sigma _m = \frac{\sigma }{\sqrt{N}}\]
де\(σ\) - стандартне відхилення і розмір\(N\) вибірки. При обчисленні в вибірці оцінка стандартної похибки середнього дорівнює:
\[s_m = \frac{s}{\sqrt{N}}\]
Стандартний нормальний розподіл
Стандартне нормальне розподіл є нормальним розподілом із середнім значенням\(0\) і стандартним відхиленням\(1\).
Стандартний бал/Стандартизувати/Стандартне нормальне\(Z\) відхилення/оцінка
Кількість стандартних відхилень балів становить від середнього показника його чисельності. Термін «стандартний бал» зазвичай використовується для нормальних популяцій; терміни «\(Z\)оцінка» та «нормальне відхилення» слід використовувати лише стосовно нормальних розподілів. Перетворення з необробленого рахунку\(X\) в\(Z\) рахунок може бути зроблено за такою формулою:
\[Z = \frac{X - \mu}{\sigma }\]
Перетворення змінної таким чином називається «стандартизацією» змінної. Слід мати на увазі, що якщо\(X\) вона не розподілена нормально, то перетворена змінна також не буде нормально розподілена.
Стандартизація/Стандартний бал
Змінна стандартизована, якщо вона має середнє значення\(0\) і стандартне відхилення\(1\). Перетворення від необробленого балу\(X\) до стандартного балу можна здійснити за такою формулою:
\[X_{standardized} = \frac{X - \mu}{\sigma }\]
де\(μ\) - середнє і\(σ\) є стандартним відхиленням. Перетворення змінної таким чином називається «стандартизацією» змінної. Слід мати на увазі, що якщо\(X\) вона не розподілена нормально, то перетворена змінна також не буде нормально розподілена.
Статистика/Статистика
- Те, що ви вивчаєте прямо зараз, також відомий як статистичний аналіз, або статистичний висновок. Це область дослідження, пов'язана з узагальненням даних, інтерпретацією даних та прийняттям рішень на основі даних.
- Кількість, розрахована у вибірці для оцінки значення в популяції, називається «статистикою».
Відображення стебла та листя
Квазіграфічне зображення числових даних. Як правило, всі, крім кінцевої цифри кожного значення, це стебло, кінцева цифра - лист. Стебла розміщуються у вертикальному списку, причому кожен зібраний лист з одного боку. Вони можуть бути дуже корисні для візуалізації невеликих наборів даних з не більше двох значущих цифр. Приклад наведено нижче. У цьому прикладі ви множите стебла на\(10\) і додаєте значення листа, щоб отримати числове значення. Таким чином, максимальна кількість проходів тачдауна становить\(3 \times 10 + 7 = 37\).
Стебло і лист відображення кількості проходів приземлення:
\[\begin{array}{c|c c c c c c c c c c c c c c c } 3 & 2 & 3 & 3 & 7 \\ 2 &0 &0 &1 &1 &1 &2 &2 &2 &3 &8 &8 &9\\ 1 &2 &2 &4 &4 &4 &5 &6 &8 &8 &8 &8 &9 &9\\ 0 &6 &9 \end{array}\]
Крок
Одна зі складових ділянки коробки, крок в\(1.5\) рази різниця між верхнім шарніром і нижнім шарніром.
Стратифікована випадкова вибірка
При стратифікованій випадковій вибірці популяція ділиться на ряд підгруп (або пластів). Випадкові вибірки потім беруться з кожної підгрупи з розмірами вибірки, пропорційними розміру підгрупи в популяції. Наприклад, якщо населення містило рівну кількість чоловіків і жінок, і підозрюється, що змінна інтересів змінюється залежно від статі, можна провести стратифіковану випадкову вибірку, щоб застрахувати репрезентативну вибірку.
Навчальний розподіл діапазону
Вивчений розподіл діапазону використовується для перевірки різниці між найбільшим і найменшим засобами. Він схожий на\(t\) розподіл, який використовується, коли є тільки два засоби.
Правило Стерджіса
Одним із методів визначення кількості класів для гістограми, Правило Стерджіса, є прийняття\(1 + \log _2(N)\) класів, округлених до найближчого цілого числа.
Помилка суми квадратів
У лінійній регресії сума похибки квадратів є сумою квадратів похибок прогнозування. При аналізі дисперсії це сума квадратних відхилень від клітинних засобів для факторів між суб'єктами та\(\text{Subjects x Treatment}\) взаємодія для внутрішньосуб'єктних факторів.
Симетричний розподіл
При симетричному розподілі верхня і нижня половини розподілу є дзеркальними відображеннями один одного. Наприклад, в розподілі, показаному нижче, частини зверху і знизу\(50\) - дзеркальне відображення один одного. При симетричному розподілі середнє дорівнює медіані. Антонім: перекіс розподілу.

\(t\)дистрибутив
\(t\)Розподіл - це розподіл величини, вибірки з нормального розподілу, поділеного на оцінку стандартного відхилення розподілу. На практиці значення, як правило, є статистикою, такою як середнє або різниця між засобами, а стандартне відхилення - це оцінка стандартної похибки статистики. \(t\)Поширення у лептокуртіческіх.
\(t\)тест
Найчастіше проводиться перевірка значущості різниці між засобами, заснованими на розподілі t. Інші програми включають
- перевірка значущості різниці між вибірковим середнім і гіпотезованим значенням середнього і
- тестування специфічного контрасту між засобами
Третя змінна проблема
Тип плутанини, в якому третя змінна призводить до помилкового причинно-наслідкового зв'язку між двома іншими. Наприклад, міста з більшою кількістю церков мають більш високий рівень злочинності. Однак більше церков не призводять до більшої кількості злочинів, але замість цього третя змінна, населення, призводить як до більшої кількості церков, так і до більшої кількості злочинів.
Тачдаун Пас
В американському футболі тачдаун пас відбувається, коли завершений пас призводить до тачдауна. Пас може бути гравцеві в кінцевій зоні або гравцеві, який згодом забігає в кінцеву зону. Приземлення коштує\(6\) очок і дозволяє отримати шанс на одну (і за деякими правилами дві) додаткові точки (и).
Тримський
Тримея є надійною мірою центральної тенденції; це середньозважене значення\(25^{th}\)\(50^{th}\), і\(75^{th}\) процентилі. Конкретно він обчислюється наступним чином:
\[\mathrm{Trimean} = 0.25 \times 25^{th} + 0.5 \times 50^{th} + 0.25 \times 75^{th}\]
Справжня оцінка
У класичній теорії випробувань справжня оцінка - це теоретичне значення, яке представляє бал учасника тесту без помилок. Якби людина взяла паралельні форми тесту тисячі разів (припускаючи відсутність практики або втоми ефектів), середнє значення всіх їх балів було б хорошим наближенням їх істинного балу, оскільки помилка буде майже повністю усереднена. Його слід відрізняти від дійсності.
Туреччина Тест на HSD
Тест «Чесно значно відрізняється» (\(HSD\)), розроблений статистиком Джоном Тукі для перевірки всіх парних порівнянь між засобами. Тест заснований на «дослідженому розподілі діапазону».
Тест на два хвоста/Двоххвоста ймовірність/Ненаправлений
Останній крок тестування значущості передбачає обчислення ймовірності того, що статистика буде відрізнятися настільки ж або більше від параметра, зазначеного в нульовій гіпотезі, як і статистика, отримана в експерименті.
Імовірність, обчислена з урахуванням відмінностей в обох напрямках (статистика більша або менша за параметр) називається двоххвостою ймовірністю. Наприклад, якщо параметр є,\(0\) а статистика є\(12\), двохступеневою ймовірністю буде ймовірність бути або\(≤ -12\) або\(≥12\). Порівняйте з однохвостою ймовірністю, яка була б ймовірністю статистичного буття\(≥\),\(12\) якби це було напрямок, вказаний заздалегідь.
Помилка типу I
У тестуванні значущості помилка відхилення справжньої нульової гіпотези.
Помилка типу II
У тестуванні значущості, нездатність відхилити помилкову нульову гіпотезу.
неупереджений
Кажуть, що вибірка є неупередженою, коли кожна людина має рівні шанси бути обраними з населення.
Оцінювач є неупередженим, якщо він систематично не переоцінює або недооцінює оцінюваний параметр. Іншими словами, це неупереджено, якщо середнє значення розподілу вибірки статистики є параметром, який він оцінює, вибіркове середнє - це неупереджена оцінка середнього чисельності населення.
Незаплановані порівняння/Post Hoc Порівняння
Коли порівняння між засобами вирішується після перегляду даних, порівняння називається «незапланованим порівнянням» або пост-hoc порівнянням. Для незапланованих порівнянь потрібні різні статистичні тести, ніж для планових порівнянь.
Верхнє суміжне значення
Один з компонентів коробчастого графіка, вище суміжне значення є найбільшим значенням в даних нижче\(75^{th}\) процентиля.
Верхній шарнір
Верхній шарнір є однією зі складових ділянки коробки; це\(75^{th}\) процентиль.
Варіабельність/спред
Мінливість відноситься до того, наскільки значення відрізняються один від одного. Тобто, наскільки вони варіюються. Мінливість також може розглядатися як розподіл розподіл. Стандартне відхилення та напівінтерквартильний діапазон є мірами мінливості.
Змінна
Щось, що може приймати різні значення. Наприклад, різні випробовувані в експерименті важать різні суми. Тому «вага» є змінною в експерименті. Або суб'єктам можуть призначатися різні дози препарату. Це зробило б «дозування» змінною. Змінні можуть бути залежними або незалежними, якісними або кількісними, а також неперервними або дискретними.
дисперсія
Дисперсія - широко використовувана міра мінливості. Він визначається як середнє квадратне відхилення балів від середнього. Формула дисперсії, обчисленої у всій сукупності
\[\sigma ^2 = \frac{\sum (X-\mu )^2}{N}\]
де\(σ^2\) представляє дисперсію,\(μ\) це середнє значення, і\(N\) число балів.
При обчисленні в вибірці з метою оцінки дисперсії в популяції чисельність населення
\[s^2 = \frac{\sum (X-M)^2}{N-1}\]
де\(s^2\) - оцінка дисперсії,\(M\) - середнє значення вибірки, і\(N\) - кількість балів у вибірці.
Закон про суму дисперсії
Закон суми дисперсії є виразом для дисперсії суми двох змінних. Якщо змінні незалежні і, отже\(r = 0\), Пірсона, наступна формула представляє дисперсію суми та різниці змінних\(X\) і\(Y\):
\[\sigma _{X\pm Y}^{2} = \sigma _{X}^{2} + \sigma _{Y}^{2}\]
Зверніть увагу, що ви додаєте відхилення для обох\(X + Y\) і\(X - Y\).
Якщо\(X\) і\(Y\) співвідносяться, то слід використовувати наступну формулу (яка перша - особливий випадок):
\[\sigma _{X\pm Y}^{2} = \sigma _{X}^{2} + \sigma _{Y}^{2} \pm 2\rho \sigma _X \sigma _Y\]
де\(ρ\) - популяційна цінність кореляції. У вибірці\(r\) використовується як кошторис\(ρ\).
Дизайн всередині предметів
Експериментальна конструкція, в якій незалежна змінна є змінною всередині суб'єктів.
Всередині суб'єктів Фактор/Змінна всередині суб'єктів/Фактор повторюваних заходів/Повторювані заходи Змінна
Змінна всередині суб'єктів - це незалежна змінна, яка маніпулюється шляхом тестування кожного предмета на кожному рівні змінної. Порівняйте з змінною між суб'єктами, в якій для кожного рівня змінної використовуються різні групи суб'єктів.
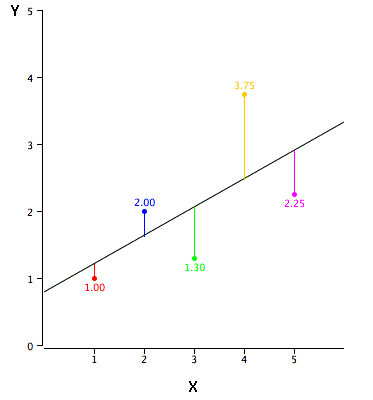
Y-Перехоплення
\(Y\)-Перехоплення лінії - це значення в точці,\(Y\) в якій лінія перехоплює\(Y\) вісь. Це значення,\(Y\) коли\(X\) дорівнює\(0\). \(Y\)Перехоплення чорної лінії, показаної на графіку, є\(0.785\).
\(Z\)бал/стандартний бал/стандартизувати/стандартне нормальне відхилення
Кількість стандартних відхилень балів становить від середнього показника його чисельності. Термін «стандартний бал» зазвичай використовується для нормальних популяцій; терміни «\(Z\)оцінка» та «нормальне відхилення» слід використовувати лише стосовно нормальних розподілів. Перетворення з необробленого рахунку\(X\) в\(Z\) рахунок може бути зроблено за такою формулою:
\[Z = \frac{X-\mu }{\sigma }\]
Перетворення змінної таким чином називається «стандартизацією» змінної. Слід мати на увазі, що якщо\(X\) вона не розподілена нормально, то перетворена змінна також не буде нормально розподілена.
