19.4: Пояснення частки дисперсії
- Page ID
- 98269
Цілі навчання
- Вкажіть різницю в ухилі між\(η^2\) і\(ω^2\)
- Обчислення\(η^2\) обчислювальних\(ω^2\)
- Розрізняють\(ω^2\) і часткові\(ω^2\)
- Вкажіть упередженість\(R^2\) і що можна зробити, щоб зменшити його
Розміри ефектів часто вимірюються з точки зору частки дисперсії, поясненої змінною. У цьому розділі ми обговорюємо цей спосіб вимірювання розміру ефекту як у конструкціях ANOVA, так і в кореляційних дослідженнях.
Проекти ANOVA
Відповіді суб'єктів будуть відрізнятися майже в кожному експерименті. Розглянемо, наприклад, кейс «Усмішки і поблажливість». Гістограма залежної змінної «поблажливість» показана на малюнку\(\PageIndex{1}\). Зрозуміло, що бали поблажливості значно різняться. Є багато причин, чому бали відрізняються. Один, звичайно, полягає в тому, що суб'єктам було призначено чотири різні умови посмішки, і стан, в якому вони перебували, може вплинути на їх бал поблажливості. Крім того, цілком ймовірно, що деякі предмети, як правило, більш поблажливі, ніж інші, тим самим сприяючи різниці між балами. Існує багато інших можливих джерел відмінностей у рейтингах поблажливості, включаючи, можливо, те, що деякі суб'єкти перебували в кращому настрої, ніж інші, та/або що деякі суб'єкти реагували більш негативно, ніж інші, на зовнішній вигляд або манери стимулюючої людини. Ви можете собі уявити, що існує безліч інших причин, чому оцінки предметів можуть відрізнятися.
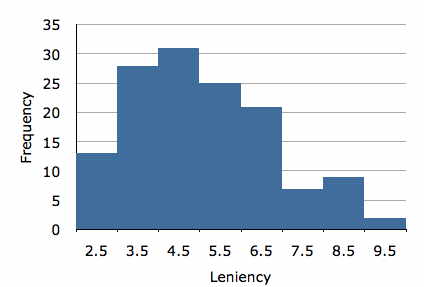
Одним із способів вимірювання впливу умов є визначення частки дисперсії між оцінками суб'єктів, що припадає на умови. У цьому прикладі дисперсія балів є\(2.794\). Питання полягає в тому, як ця дисперсія порівнюється з тим, якою була б дисперсія, якби кожен суб'єкт був у тому ж стані лікування. Ми оцінюємо це, обчислюючи дисперсію в межах кожної з умов лікування та приймаючи середнє значення цих відхилень. Для цього прикладу середнє значення відхилень є\(2.649\). Оскільки середня дисперсія в умовах посмішки не набагато менше, ніж дисперсія ігноруючи умови, зрозуміло, що «Умова посмішки» не несе відповідальності за високий відсоток дисперсії балів. Найзручніший спосіб обчислення поясненої пропорції - через суму квадратів «умови» і суму квадратів загальної. Обчислення цих сум квадратів наведені в розділі про ANOVA. Для наведених даних сума квадратів для «Умови посмішки» дорівнює,\(27.535\) а сума квадратів загальна дорівнює\(377.189\). Тому пропорція, пояснена «Стан посмішки», становить:
\[\frac{27.535}{377.189} = 0.073\]
Таким чином,\(0.073\) або\(7.3\%\) дисперсія пояснюється «Стан посмішки».
Альтернативним способом поглянути на пояснену дисперсію є зменшення пропорції похибки. Сума квадратів total (\(377.189\)) представляє варіацію, коли «Умова посмішки» ігнорується, а сума квадратів error (\(377.189 - 27.535 = 349.654\)) є варіацією, що залишилася, коли враховується «Умова посмішки». Різниця між\(377.189\) і\(349.654\) є\(27.535\). Це зменшення похибки\(27.535\) являє собою пропорційне зменшення\(27.535/377.189 = 0.073\), таке ж значення, яке обчислюється з точки зору частки дисперсії пояснюється.
Ця міра розміру ефекту, незалежно від того, обчислюється з точки зору дисперсії, поясненої або з точки зору зменшення відсотка похибки,\(η\) називається\(η^2\) де грецька буква ета. На жаль,\(η^2\) має тенденцію завищувати пояснену дисперсію і тому є упередженою оцінкою частки дисперсії пояснюється. Як такий, не рекомендується (незважаючи на те, що про це повідомляє провідний пакет статистики).
Альтернативна міра,\(ω^2\) (омега в квадраті), є неупередженим і може бути обчислена з
\[\omega ^2 = \frac{SSQ_{condition}-(k-1)MSE}{SSQ_{total}+MSE}\]
де\(MSE\) - середня квадратна похибка і\(k\) кількість умов. Для цього прикладу\(k = 4\) і\(ω^2 = 0.052\).
Важливо знати, що як мінливість вибіркової популяції, так і конкретні рівні незалежної змінної є важливими детермінантами частки дисперсії, поясненої. Розглянемо дві можливі конструкції експерименту, що вивчає вплив споживання алкоголю на здатність водіння. Як видно з таблиці\(\PageIndex{1}\),\(\text{Design 1}\) має менший діапазон доз і більш різноманітну популяцію, ніж\(\text{Design 2}\). Які наслідки для частки дисперсії пояснюється дозою? Варіація через дозу буде більшою\(\text{Design 2}\), ніж\(\text{Design 1}\) оскільки алкоголь маніпулюється сильніше, ніж в\(\text{Design 1}\). Однак дисперсія в чисельності населення повинна бути більшою,\(\text{Design 1}\) оскільки вона включає більш різноманітний набір водіїв. Оскільки з\(\text{Design 1}\) дисперсією через Dose буде меншою, а загальна дисперсія буде більшою, частка дисперсії, пояснена Dose, буде набагато меншою,\(\text{Design 1}\) ніж використання\(\text{Design 2}\). Таким чином, пояснена частка дисперсії не є загальною характеристикою незалежної змінної. Натомість це залежить від конкретних рівнів незалежної змінної, що використовується в експерименті, та мінливості вибіркової популяції.
|
Дизайн |
Доза |
Населення |
|
1 |
0.00 |
Всі водії віком від 16 до 80 років |
|
0,30 |
||
|
0,60 |
||
|
2 |
0.00 |
Досвідчені водії віком від 25 до 30 років |
|
0,50 |
||
|
1.00 |
Факторіальні конструкції
У однофакторних конструкціях сума квадратів загальна є умовою суми квадратів плюс сума похибки квадратів. Частка роз'ясненої дисперсії визначена відносно загальної суми квадратів. У\(A \times B\) дизайні є три джерела варіації (\(A, B, A \times B\)) на додаток до помилки. Частка дисперсії, пояснена для змінної (наприклад)\(A\), може бути визначена відносно суми квадратів total (\(SSQ_A + SSQ_B + SSQ_{A\times B} + SSQ_{error}\)) або відносно\(SSQ_A + SSQ_{error}\).
Для ілюстрації на прикладі розглянемо гіпотетичний експеримент щодо впливу віку (\(6\)і\(12\) років) і методів навчання читання (експериментальні та контрольні умови). Засоби наведені в табл\(\PageIndex{2}\). Стандартне відхилення кожної з чотирьох осередків (\(Age \times Treatment\)комбінацій) дорівнює\(5\). (Природно, для реальних даних стандартні відхилення не були б точно рівними, а кошти не були б цілими числами.) Нарешті, були\(10\) предмети на клітинку, в результаті чого в цілому\(40\) суб'єктів.
| Лікування | ||
|---|---|---|
| Вік | Експериментальний | Контроль |
| 6 | 40 | 42 |
| 12 | 50 | 56 |
Джерела варіації, ступеня свободи та суми квадратів з аналізу зведеної таблиці дисперсій, а також чотири міри розміру ефекту наведені в табл\(\PageIndex{3}\). Зверніть увагу, що сума квадратів за віком дуже велика щодо двох інших ефектів. Це те, що можна було б очікувати, оскільки різниця в здатності до читання між\(6\) - і\(12\) -річними дуже велика щодо ефекту стану.
| Джерело | дф | SSQ | \(η^2\) | частковий \(η^2\) |
\(ω^2\) | частковий \(ω^2\) |
|---|---|---|---|---|---|---|
| Вік | 1 | 1440 | \ (η ^ 2\) ">0,567 | \ (η ^ 2\) ">0,615 | \ (ω^2\) ">0.552 | \ (ω^2\) ">0.586 |
| Стан | 1 | 160 | \ (η ^ 2\) ">0,063 | \ (η ^ 2\) ">0.151 | \ (ω^2\) ">0.053 | \ (ω^2\) ">0,119 |
| А х С | 1 | 40 | \ (η ^ 2\) ">0,016 | \ (η ^ 2\) ">0,043 | \ (ω^2\) ">0,006 | \ (ω^2\) ">0,015 |
| Помилка | 36 | 900 | ||||
| Всього | 39 | 2540 |
Спочатку розглянемо два методи обчислень\(η^2\), мічені\(η^2\) і часткові\(η^2\). Значення\(η^2\) для ефекту - це просто сума квадратів для цього ефекту, поділена на загальну суму квадратів. Наприклад,\(η^2\) для Вік є\(1440/2540 = 0.567\). Як і в однофакторної конструкції,\(η^2\) пропорція загальної варіації пояснюється змінною. Часткова\(η^2\) для Вік\(SSQ_{Age}\) ділиться на (\(SSQ_{Age} + SSQ_{error}\)), що є\(1440/2340 = 0.615\).
Як бачите,\(η^2\) часткова більше, ніж\(η^2\). Це пояснюється тим, що знаменник менший для часткового\(η^2\). Різниця між\(η^2\) частковою\(η^2\) і ще більшою для впливу стану. Це тому, що\(SSQ_{Age}\) є великим, і це робить велику різницю, включений він у знаменник чи ні.
Як зазначалося раніше, краще використовувати,\(ω^2\) ніж\(η^2\) тому, що\(η^2\) має позитивний ухил. Ви можете бачити, що значення для менше\(ω^2\), ніж для\(η^2\). Розрахунки для\(ω^2\) наведені нижче:
\[\omega ^2 = \frac{SSQ_{effect}-df_{effect}MS_{error}}{SSQ_{total}+MS_{error}}\]
\[\omega _{partial}^2 = \frac{SSQ_{effect}-df_{effect}MS_{error}}{SSQ_{effect}+(N-df_{effect})MS_{error}}\]
де\(N\) - загальна кількість спостережень.
Вибір того, чи використовувати\(ω^2\) чи часткове,\(ω^2\) є суб'єктивним; жоден не є правильним чи неправильним. Однак важливо зрозуміти різницю і, якщо ви використовуєте комп'ютерне програмне забезпечення, знати, яка версія обчислюється. (Остерігайтеся, принаймні один програмний пакет неправильно позначає статистику).
Кореляційні дослідження
У розділі «Розбиття сум квадратів» в розділі «Регресія» ми побачили, що сума квадратів для\(Y\) (змінна критерію) може бути розділена на суму пояснених квадратів і суму квадратів похибки. Отже, частка дисперсії, пояснена множинною регресією, є:
\[SSQ_{explained}/SSQ_{total }\]
У простій регресії частка дисперсії пояснюється дорівнює\(r^2\); при множинній регресії вона дорівнює\(R^2\).
Загалом,\(R^2\) є аналогом\(η^2\) і є упередженою оцінкою поясненої дисперсії. Наступна формула коригування\(R^2\) аналогічна\(ω^2\) і менш упереджена (хоча і не зовсім неупереджена):
\[R_{adjusted}^{2} = 1 - \frac{(1-R^2)(N-1)}{N-p-1}\]
де\(N\) - загальна кількість спостережень і\(p\) число змінних предиктора.
