14.4: Стандартна помилка кошторису

Last updated
Save as PDF

Page ID: 98188

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Складіть судження про розмір стандартної похибки кошторису з розкидного графіка
Обчислити стандартну похибку оцінки на основі похибок прогнозування
Обчислити стандартну помилку, використовуючи кореляцію Пірсона
Оцініть стандартну похибку кошторису на основі вибірки

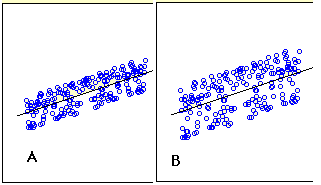
\(\PageIndex{1}\)На малюнку показані два приклади регресії. Ви можете бачити, що в\(\text{Graph A}\), точки знаходяться ближче до лінії, ніж вони знаходяться в\(\text{Graph B}\). Тому прогнози в більш\(\text{Graph A}\) точні, ніж в\(\text{Graph B}\).

Малюнок\(\PageIndex{1}\): Регресії, що відрізняються точністю прогнозування

Стандартна похибка оцінки - міра точності прогнозів. Нагадаємо, що лінія регресії - це лінія, яка мінімізує суму квадратних відхилень прогнозування (також називається помилкою суми квадратів). Стандартна похибка кошторису тісно пов'язана з цією величиною і визначається нижче:

\[\sigma _{est}=\sqrt{\frac{\sum (Y-Y')^2}{N}}\]

де\(\sigma _{est}\) стандартна похибка оцінки,\(Y\) є фактичним балом,\(Y'\) є прогнозованим балом, і\(N\) є кількістю пар балів. Чисельник - це сума квадратних відмінностей між фактичними балами та прогнозованими балами.

Відзначимо схожість формули\(\sigma _{est}\) для з формулою для σ. Виходить, що σ est - це стандартне відхилення похибок прогнозування (кожна\(Y - Y'\) - похибка прогнозування).

Припустимо, що дані в таблиці\(\PageIndex{1}\) є даними з популяції з п'яти\(X\)\(Y\) пар.

Таблиця\(\PageIndex{1}\): Приклад даних
	Х	У	Y'	Y-Y'	(Y-Y') ²
	1.00	1.00	1.210	-0.210	0,044
	2.00	2.00	1,635	0,365	0.133
	3.00	1.30	2.060	-0.760	0,578
	4.00	3.75	2.485	1.265	1.600
	5.00	2.25	2.910	-0.660	0,436
Сума	15.00	10.30	10.30	0.000	2.791

Останній стовпець показує, що сума квадратів похибок прогнозування дорівнює\(2.791\). Тому стандартна похибка кошторису становить

\[\sigma _{est}=\sqrt{\frac{2.791}{5}}=0.747\]

Існує версія формули стандартної помилки з точки зору кореляції Пірсона:

\[\sigma _{est}=\sqrt{\frac{(1-\rho )^2SSY}{N}}\]

де\(ρ\) - популяційна цінність кореляції Пірсона і\(SSY\)

\[SSY=\sum (Y-\mu _Y)^2\]

Для даних у таблиці\(\PageIndex{1}\)\(μ_Y = 2.06\),\(SSY = 4.597\) і\(ρ= 0.6268\). Тому,

\[\sigma _{est}=\sqrt{\frac{(1-0.6268^2)(4.597)}{5}}=\sqrt{\frac{2.791}{5}}=0.747\]

яке є тим самим значенням, обчисленим раніше.

Подібні формули використовуються, коли стандартна похибка оцінки обчислюється з вибірки, а не сукупності. Різниця лише в тому, що знаменник - це\(N-2\) скоріше ніж\(N\). Причина\(N-2\) використовується, а не в\(N-1\) тому, що два параметри (нахил і перехоплення) були оцінені для того, щоб оцінити суму квадратів. Формули для вибірки, порівнянної з тими для популяції, наведені нижче.

\[s _{est}=\sqrt{\frac{\sum (Y-Y')^2}{N-2}}\]

\[s _{est}=\sqrt{\frac{2.791}{3}}=0.964\]

\[s _{est}=\sqrt{\frac{(1-r)^2SSY}{N-2}}\]