Skip to main content
LibreTexts - Ukrayinska

9.E: Розподіл вибірки (вправи)

  1. Last updated
  2. Save as PDF
  • Page ID
    98339

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Для деяких з цих вправ ви можете скористатися калькулятором «r to z» та аплетом «Обчислити площу для заданого X».

    Загальні питання

    Q1

    Населення має середнє значення\(50\) і стандартне відхилення\(6\).

    1. Для чого означають середнє і стандартне відхилення розподілу вибірки середнього значення\(N = 16\)?
    2. Для чого означають середнє і стандартне відхилення розподілу вибірки середнього значення\(N = 20\)? (відповідний розділ)

    Q2

    З огляду на тест, який нормально розподіляється із середнім значенням\(100\) і стандартним відхиленням\(12\), знайдіть:

    1. ймовірність того, що один бал, набраний випадковим чином, буде більше\(110\) (відповідний розділ)
    2. ймовірність того, що вибірка\(25\) балів матиме середнє значення більше\(105\) (відповідний розділ)
    3. ймовірність того, що вибірка\(64\) балів матиме середнє значення більше\(105\) (відповідний розділ)
    4. ймовірність того, що середнє значення вибірки\(16\) балів буде або менше,\(95\) або більше\(105\) (відповідний розділ)

    Q3

    Який термін відноситься до стандартного відхилення розподілу вибірки? (відповідний розділ)

    Q4

    1. Якщо стандартна похибка середнього значення\(10\) для\(N = 12\), для чого потрібна стандартна похибка середнього\(N = 22\)?
    2. Якщо стандартна похибка середнього значення\(50\) для\(N = 25\), для чого вона потрібна\(N = 64\)? (відповідний розділ)

    Q5

    Розроблено анкету для оцінки ставлення жінок та чоловіків до використання тварин у дослідженнях. Одне питання запитує, чи є дослідження тварин неправильним і відповідає за\(7\) -бальної шкалою. Припустимо, що в популяції середнє значення для жінок є\(5\), середнє значення для чоловіків є\(4\), а стандартне відхилення для обох груп -\(1.5\). Припустимо, що бали зазвичай розподіляються. Якщо\(12\) жінки і\(12\) чоловіки вибираються випадковим чином, яка ймовірність того, що середнє значення жінок буде більше, ніж\(1.5\) бали вище середнього показника чоловіків? (відповідний розділ)

    Q6

    Якби кореляція між досягненнями читання та математичними досягненнями у населення п'ятикласників була б ймовірність того\(0.60\), що у вибірці\(28\) учнів коефіцієнт кореляції вибірки був би більше\(0.65\)? (відповідний розділ)

    Q7

    Якби численні зразки\(N = 15\) взяті з рівномірного розподілу і провести відносний частотний розподіл засобів, якою буде форма частотного розподілу? (відповідний розділ та відповідний розділ)

    Q8

    Нормальний розподіл має середнє значення\(20\) і стандартне відхилення\(10\). Дві бали вибираються випадковим чином з розподілу, а другий бал віднімається від першого. Яка ймовірність того, що показник різниці буде більше\(5\)? Підказка: Прочитайте розділ Закон про суму дисперсії глави 3. (відповідний розділ та відповідний розділ)

    Q9

    Яка форма розподілу вибірки\(r\)? Яким чином форма залежить від чисельності кореляції населення? (відповідний розділ)

    Q10

    Якщо ви виберете одне число зі стандартного нормального розподілу, яка ймовірність це буде\(0.5\)? (відповідний розділ та відповідний розділ)

    Q11

    Змінна зазвичай розподіляється із середнім значенням\(120\) і стандартним відхиленням\(5\). Чотири бали випадковим чином вибірки. Яка ймовірність того, що середнє значення чотирьох балів вище\(127\)? (відповідний розділ)

    Q12

    Співвідношення між самооцінкою та екстраверсією є\(0.30\). \(84\)Береться зразок.

    1. Яка ймовірність того, що кореляція буде менше\(0.10\)?
    2. Яка ймовірність того, що кореляція буде більше\(0.25\)? (відповідний розділ)

    Q13

    Середній середній бал для студентів в\(\text{School A}\) є\(3.0\); середній середній бал для студентів в\(\text{School B}\) є\(2.8\). Стандартне відхилення в обох школах є\(0.25\). Загальний бал обох шкіл, як правило, розподілені. Якщо\(9\) учні випадковим чином відбираються з кожної школи, яка ймовірність того, що:

    1. середнє значення для вибірки\(\text{School A}\) перевищить, що\(\text{School A}\) на\(0.5\) або більше? (відповідний розділ)
    2. середнє значення для зразка\(\text{School B}\) буде більше, ніж середнє значення зразка для\(\text{School A}\)? (відповідний розділ)

    Q14

    У місті,\(70\%\) з людей віддають перевагу\(\text{Candidate A}\). Припустимо,\(30\) люди з цього міста були відібрані.

    1. Що таке середнє розподіл вибірки\(p\)?
    2. Що таке стандартна помилка\(p\)?
    3. Яка ймовірність того, що\(80\%\) або більше цього зразка віддадуть перевагу\(\text{Candidate A}\)?
    4. Яка ймовірність того, що\(45\%\) або більше цього зразка віддасть перевагу якомусь іншому кандидату? (відповідний розділ)

    Q15

    При вирішенні завдань, де потрібно розподіл вибірки\(r\), в чому причина перетворення з\(r\) в\(z'\)? (відповідний розділ)

    Q16

    У популяції середній показник SAT становить\(1000\). Чи були б ви більш імовірними (або однаково ймовірними) отримати середнє значення зразка,\(1200\) якщо ви випадковим чином\(10\) відібрали студентів або якщо ви випадково вибрали\(30\) студентів? Поясніть. (відповідний розділ та відповідний розділ)

    Q17

    True/false: Стандартна похибка середнього значення менше\(N = 20\), коли коли\(N = 10\). (відповідний розділ)

    Q18

    True/false: Розподіл вибірки\(r =0.8\) стає нормальним у міру\(N\) збільшення. (відповідний розділ)

    КВАРТАЛ 19

    True/false: Ви обираєте\(20\) студентів із населення та обчислюєте середнє значення їхніх тестових балів. Ви повторюєте цей процес\(100\) раз і намічаєте розподіл кошти. В даному випадку розмір вибірки дорівнює\(100\). (відповідний розділ та відповідний розділ)

    Q20

    Правда/неправда: У вашій школі учні\(40\%\) дивляться телевізор вночі. Ви випадково запитуєте\(5\) студентів щодня, чи дивляться вони телевізор вночі. Щодня ви знайдете, що\(2\) ви\(5\) дивитеся телевізор вночі. (відповідний розділ та відповідний розділ)

    Q21

    True/false: Медіана має розподіл вибірки. (відповідний розділ)

    Q22

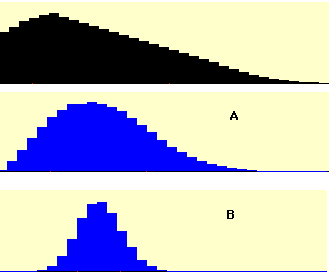
    True/false: Зверніться до малюнка нижче. Розподіл населення показано чорним кольором, а відповідний розподіл вибірки середнього значення для\(N = 10\) позначено\(A\) "" (відповідний розділ та відповідний розділ)

    clt.gif

    Питання з тематичних досліджень

    Наступні питання використовують дані з тематичного дослідження Angry Moods (AM).

    Q23

    1. Скільки чоловіків було відібрано?
    2. Скільки жінок було відібрано?

    Q24

    Яка середня різниця між чоловіками та жінками на балах Anger-Out?

    Q25

    Припустимо, у населення оцінка Anger-Out для чоловіків на два бали вище, ніж у жінок. Розбіжності населення для чоловіків і жінок є обома\(20\). Припустимо, що оцінки Anger-Out для обох статей зазвичай розподіляються. З огляду на цю інформацію про параметри популяції:

    1. Що означає розподіл вибірки різниці між засобами? (відповідний розділ)
    2. У чому стандартна похибка різниці між засобами? (відповідний розділ)
    3. Яка ймовірність того, що ви отримали б цю середню різницю (див. #24) або менше у вашому зразку? (відповідний розділ)

    Наступні питання використовують дані з тематичного дослідження Animal Research (AR).

    Q26

    Скільки людей було відібрано, щоб дати свою думку про дослідження тварин?

    Q27

    (AR #11) Яка кореляція в цьому зразку між переконанням, що дослідження тварин є неправильним, і переконанням, що дослідження тварин необхідні? (Гл. 4.E)

    Q28

    Припустимо, кореляція між переконанням, що дослідження тварин є неправильним, і переконанням, що дослідження тварин необхідні, є\(-0.68\) в популяції.

    1. Перетворити\(-0.68\) на\(z'\). (відповідний розділ)
    2. Знайдіть стандартну похибку цього розподілу вибірки. (відповідний розділ)
    3. У новому зразку, яка ймовірність того, що ви отримаєте кореляцію, знайдену в вихідному зразку (див. #27) або нижчу кореляцію (ближче до\(-1\))? (відповідний розділ)

    Вибрані відповіді

    S1

    1. Середнє =\(50\), SD =\(1.5\)

    S2

    1. \(0.019\)

    S4

    1. \(7.39\)

    S11

    \(0.0026\)

    S12

    1. \(0.690\)

    S13

    1. \(0.0055\)

    S 14

    1. \(0.116\)

    S23

    1. \(30\)

    S25

    1. \(2\)

    S28

    1. \(0.603\)