9.8: Розподіл вибірки р
- Page ID
- 98383
Цілі навчання
- Створіть взаємозв'язок між розподілом вибірки p і нормальним розподілом
Припустимо, що в передвиборній гонці між\(\text{Candidate A}\) і\(\text{Candidate B}\),\(0.60\) з виборців віддають перевагу\(\text{Candidate A}\). Якби була опитана випадкова вибірка\(10\) виборців, навряд чи саме\(60\%\) з них (\(6\)) воліли б\(\text{Candidate A}\). Випадково частка в зразку, що віддає перевагу,\(\text{Candidate A}\) може бути легко трохи нижче\(0.60\) або трохи вище, ніж\(0.60\). Розподіл вибірки\(p\) - це розподіл, який буде результатом, якщо ви неодноразово відбирали\(10\) виборців та визначали пропорцію (\(p\)), яка надала перевагу\(\text{Candidate A}\).
Розподіл вибірки\(p\) - це окремий випадок розподілу вибірки середнього. Таблиця\(\PageIndex{1}\) показує гіпотетичну випадкову вибірку\(10\) виборців. Тим, хто віддає перевагу\(\text{Candidate A}\), дають бали,\(1\) а тим, хто віддає перевагу\(\text{Candidate B}\), дають бали\(0\). Зауважте, що сім виборців вважають за краще,\(\text{Candidate A}\) щоб вибіркова пропорція (\(p\))
\[p = \frac{7}{10} = 0.70\]
Як бачите,\(p\) це середнє значення\(10\) переваг балів.
| Виборця | Перевага |
|---|---|
| 1 | 1 |
| 2 | 0 |
| 3 | 1 |
| 4 | 1 |
| 5 | 1 |
| 6 | 0 |
| 7 | 1 |
| 8 | 0 |
| 9 | 1 |
| 10 | 1 |
Розподіл тісно\(p\) пов'язаний з біноміальним розподілом. Біноміальний розподіл - це розподіл загальної кількості успіхів (що сприяє\(\text{Candidate A}\), наприклад), тоді як розподіл\(p\) - це розподіл середньої кількості успіхів. Середнє значення, звичайно, є загальним, поділеним на розмір вибірки,\(N\). Тому розподіл вибірки\(p\) та біноміальний розподіл відрізняються тим, що\(p\) є середнім значенням балів (\(0.70\)), а біноміальний розподіл стосується загальної кількості успіхів (\(7\)).
Біноміальний розподіл має середнє значення
\[\mu =N\pi\]
Розділивши на\(N\) коригувати для того, що розподіл вибірки\(p\) має справу із засобами замість підсумків, ми виявимо, що середнє значення розподілу вибірки\(p\) є:
\[\mu _p=\pi\]
Стандартне відхилення біноміального розподілу становить:
\[\sqrt{N\pi(1-\pi )}\]
Розділивши на\(N\)\(p\) тому, що це означає, що не загальна, ми знаходимо стандартну помилку\(p\):
\[\sigma _p=\frac{\sqrt{N\pi(1-\pi )}}{N}=\sqrt{\frac{\pi(1-\pi )}{N}}\]
Повертаючись до прикладу виборця,\(\pi =0.60\) і\(N = 10\). (Не плутайте\(\pi =0.60\), частка населення та\(p = 0.70\) частка вибірки.) Тому середнє значення розподілу вибірки\(p\) є\(0.60\). Стандартна помилка
\[\sigma _p=\sqrt{\frac{0.60(1-0.60)}{10}}=0.155\]
Розподіл вибірки\(p\) є дискретним, а не безперервним розподілом. Наприклад, з\(N\) одним з\(10\), можна мати a\(0.50\) або a\(p\)\(p\) з,\(0.60\) але не a\(p\) з\(0.55\).
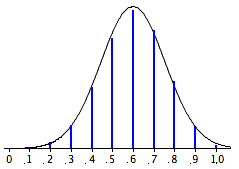
Розподіл вибірки приблизно нормально розподіляється, якщо\(N\) він досить великий і\(\pi\) не близький до\(0\) або\(1\).\(p\) Емпіричне правило полягає в тому, що наближення добре, якщо\(N(1-\pi )\) обидва\(N\pi\) і більше\(10\). Розподіл вибірки для прикладу виборця наведено на малюнку\(\PageIndex{1}\). Зверніть увагу, що хоча і\(N(1-\pi )\) є лише\(4\), наближення є досить хорошим.