Цілі навчання
- Який найкращий спосіб вимірювання чуйності попиту?
- Який найкращий спосіб вимірювання чуйності постачання?
\(x (p)\)Дозволяти представляти кількість, придбану, коли ціна р, так що функція х представляє попит. Наскільки реагує попит на зміну цін? Може виникнути спокуса використовувати похідну\(x′\), щоб виміряти чуйність попиту, оскільки він вимірює, наскільки кількість вимагала змін у відповідь на невелику зміну ціни. Однак цей захід має дві проблеми. По-перше, він чутливий до зміни одиниць. Якщо я вимірюю кількість цукерок в кілограмах, а не в фунтах, похідна попиту на цукерки щодо ціни змінюється, навіть якщо сам попит незмінний. По-друге, якщо я поміняю цінові одиниці, конвертуючи з однієї валюти в іншу, знову похідна попиту зміниться. Тож похідна є незадовільною як міра чуйності, оскільки вона залежить від одиниць виміру. Поширеним способом встановлення міри без одиниць є використання відсотків, і це передбачає врахування чуйності попиту на невелику процентну зміну ціни в процентному співвідношенні. Це поняття еластичності попиту. Концепція пружності була придумана Альфредом Маршаллом (1842—1924) у 1881 році, сидячи на своєму даху. Еластичність попиту - це процентне зменшення кількості, яке є результатом невеликого процентного зростання ціни. Формально еластичність попиту, яка, як правило, позначається грецькою літерою epsilon, ε, (вибирається мнемонічно для позначення еластичності) становить
\ begin {рівняння}\ варепсилон = -д х х д р = -р х г х д р = -р х ^ {\ прайм} (р) х (р)\ кінець {рівняння}
Знак мінус включається в вираз, щоб зробити еластичність позитивним числом, так як попит знижується. Для початку переконаємося, що еластичність, по суті, вільна від одиниці. Зміна вимірювання x не впливає на еластичність, оскільки коефіцієнт пропорційності з'являється як у чисельнику, так і в знаменнику. Аналогічно, зміна міри ціни так, що p замінюється r = ap, не змінює еластичності, оскільки, як показано нижче,
\ begin {рівняння}\ варепсилон = -р д г х (р/а) х (р/а) =-r x ^ {\ prime} (r/a) 1 a x (r/a) =-p x ^ {\ prime} (p) x (p)\ кінець {рівняння}
міра пружності не залежить від а, а значить, не впливає на зміну одиниць.
Як витрати споживача, також відомі як (індивідуальний) загальний дохід, реагують на зміну ціни? Споживач купує x (p) за ціною p, і, таким чином, загальні витрати, або загальний дохід, становить TR = px (p). Таким чином,
\ почати {рівняння} д\ текст {дп} р х (р) =х (р) +р х ^ {\ правий} (р) =х (р)\ лівий (1+р х ^ {\ правий} (р) х (р)\ праворуч) = х (р) (1-\ варепсилон)\ кінець {рівняння}
Тому,
\[d dp TR 1 p TR =1−ε.\]
Іншими словами, процентна зміна загальної виручки в результаті зміни ціни на 1% становить один мінус еластичність попиту. Таким чином, зростання ціни на 1% збільшить загальний дохід, коли еластичність попиту менше одиниці, що визначається як нееластичний попит. Зростання цін зменшить загальний дохід, коли еластичність попиту перевищує одиницю, що визначається як еластичний попит. Випадок еластичності, рівної одиниці, називається унітарною еластичністю, а сумарна виручка незмінна невеликою зміною ціни. Більш того, це процентне зростання ціни збільшить виручку приблизно на 1 — ε відсоток. Оскільки часто можна оцінити еластичність попиту, формули можуть бути легко використані на практиці. У таблиці 3.1 наведені оцінки еластичності попиту на різні вироби.
Таблиця 3.1 Різні еластичності попиту
| Продукт |
Продукт |
ε |
| Сіль |
Фільми |
0.9 |
| Матчі |
Молюски, що вживаються в домашніх умовах |
0.9 |
| Зубочистки |
Шини короткочасні |
0.9 |
| Авіакомпанія подорожі, короткострокові |
Устриці, що вживаються в домашніх умовах |
1.1 |
| Житловий природний газ, короткочасний |
Приватна освіта |
1.1 |
| Бензиновий, короткочасний |
Житло, власник зайнятий, довгостроковий |
1.2 |
| Автомобілі, довгострокові |
Шини довготривалі |
1.2 |
| Кава |
Радіо- і телевізійні приймачі |
1.2 |
| Юридичні послуги, короткострокові |
Автомобілі, короткострокові |
1,2-1,5 |
| Тютюнові вироби короткострокові |
Харчування в ресторані |
2.3 |
| Житловий природний газ, довгостроковий |
Авіакомпанія, довгострокова |
2.4 |
| Риба (тріска), що вживається в домашніх умовах |
Свіжий зелений горошок |
2.8 |
| Послуги лікаря |
Закордонні подорожі, довгострокові |
4.0 |
| Таксі, короткостроковий |
Автомобілі Шевроле |
4.0 |
| Бензиновий, довгостроковий |
Свіжі помідори |
4.6 |
З http://www.mackinac.org/archives/1997/s1997-04.pdf; цитуються джерела: Джеймс Д. Гвартні та Річард Л.Строуп, Економіка: приватний та громадський вибір, 7-е видання, 1995; 8-е видання, 1997; Хендрік С. Хаутаккер і Лестер Тейлор, Споживчий попит в США, 1929—1970 (1966; Кембридж: Гарвард Університетська преса, 1970); Дуглас Бохі, Аналіз поведінки попиту (Балтімор: Університетська преса Джона Хопкінса, 1981); Хайнг-Тай Ченг та Оральні каппи молодший, «Попит на рибу», Американський журнал аграрної економіки, серпень 1988 року; і Міністерство сільського господарства США.
Коли попит лінійний\(\begin{equation}x(p)=a-b p\end{equation}\), еластичність попиту має вигляд
\ begin {рівняння}\ varepsilon=\ mathrm {bp}\ mathrm {a} -\ mathrm {bp} =\ mathrm {p}\ text {a}\ mathrm {b} -\ mathrm {p}\ end {рівняння}
Цей випадок проілюстрований на малюнку 3.1.
Малюнок 3.1 Еластичність для лінійного попиту
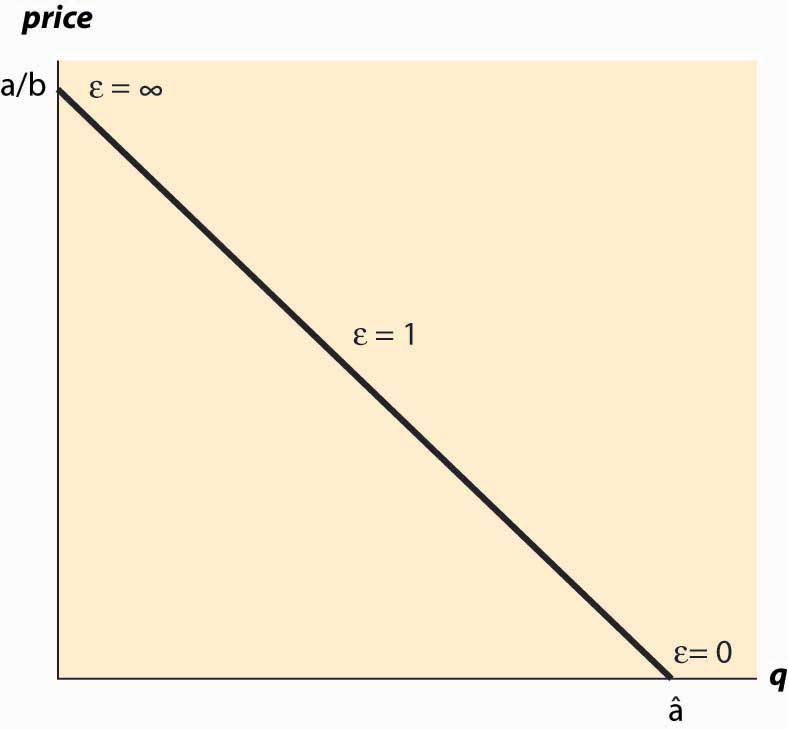
Якщо попит набуває вигляду x (p) = a* p −ε, то попит має постійну еластичність, а еластичність дорівнює ε. Іншими словами, еластичність залишається на тому ж рівні, тоді як базові змінні (такі як ціна та кількість) змінюються.
Еластичність пропозиції аналогічна еластичності попиту в тому, що вона є одиничною мірою реагування пропозиції на зміну ціни, і визначається як процентне збільшення кількості, що поставляється в результаті невеликого процентного зростання ціни. Формально, якщо s (p) дає кількість, що поставляється для кожної ціни p, еластичність пропозиції, що позначається η (грецька буква «ета», вибрана тому, що епсилон вже був прийнятий) дорівнює
\ begin {рівняння}\ eta=\ ім'я оператора {ds}\ математика {s}\ математика {dp}\ математика {p} =\ математика {p}\ математика {s}\ математика {dp} =\ математика {ps} ^ {\ prime} (\ mathrm {p})\ mathrm {s} (\ mathrm {p})\ end {рівняння}
Знову ж таки, аналогічно попиту, якщо пропозиція приймає вигляд s (p) = a* p η, то пропозиція має постійну еластичність, а еластичність дорівнює η. Окремим випадком цієї форми є лінійна подача, яка виникає, коли пружність дорівнює одиниці.
Ключові виноси
- Еластичність попиту - це процентне зменшення кількості, що є результатом невеликого процентного зростання ціни, яке, як правило, позначається грецькою літерою epsilon, ε.
- Відсоток зміни загальної виручки в результаті зміни ціни на 1% становить один мінус еластичність попиту.
- Еластичність попиту, яка менше одиниці, визначається як нееластичний попит. При цьому зростання ціни збільшує загальну виручку.
- Зростання цін зменшить загальний дохід, коли еластичність попиту перевищує одиницю, що визначається як еластичний попит.
- Випадок еластичності, рівної одиниці, називається унітарною еластичністю, а сумарна виручка незмінна невеликою зміною ціни.
- Якщо попит набуває вигляду x (p) = a* p −ε, то попит має постійну еластичність, а еластичність дорівнює ε.
- Еластичність пропозиції визначається як процентне збільшення кількості, що поставляється в результаті невеликого процентного зростання ціни.
- Якщо подача приймає вигляд s (p) = a* p η, то подача має постійну еластичність, а пружність дорівнює η.
ВПРАВИ
- Припустимо, споживач має постійну еластичність попиту ε, а попит еластичний\(\begin{equation}(ε > 1)\end{equation}\). Покажіть, що витрати збільшуються в міру зниження ціни.
- Припустимо, споживач має постійну еластичність попиту ε, а попит нееластичний\(\begin{equation}(ε < 1)\end{equation}\). Яка ціна робить витрати найбільшими?
- Для споживача з постійною еластичністю попиту\(\begin{equation}(ε > 1)\end{equation}\) обчислити споживчий надлишок.
- Для виробника з постійною еластичністю пропозиції обчислити прибуток виробника.

