Skip to main content
LibreTexts - Ukrayinska

6.2: Приклади

  1. Last updated
  2. Save as PDF
  • Page ID
    103195

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    1. Обчисліть периметр (або окружність, якщо це доречно) і площа наступних фігур:
      1. Обчисліть периметр і площу прямокутника, використовуючи малюнок нижче.

    clipboard_eafcdea686f8b83a164cbb09484ca6b70.png

    \(\begin{aligned} \text{Perimeter} &= \text{sum of the lengths of the sides}\\ &= \text{14 in+5 in+14 in+5 in=2(14 in)+2(5 in)} \\ &= \text{ 28 in+10 in=38 in}\end{aligned}\)

    Площа = (довжина) * (ширина) =\(\left(14\,\, in\right)\left(5\,\, in\right)=70\,\, in^2\)

    1. Обчисліть окружність і площу кола, використовуючи малюнок нижче.

    clipboard_ec875222934ed71ef4b5bca68738f038b.png

    Окружність =\(\pi \left(diameter\right)=\pi \left(6\,\, cm\right)=\left(3.14\right)\left(6\,\, cm\right)=18.84\,\, cm\)

    Площа =\(\left(0.785\right){\left(diameter\right)}^2=\left(0.785\right){\left(6\,\, cm\right)}^2=\left(0.785\right)\left(36\,\, cm^2\right)=28.26\ cm^2\)

    1. Обчисліть площу фігур нижче.
      1. Трикутник висотою 7 метрів і підставою 15 метрів.

    clipboard_eddb1017f00ea012f0610e86bc1c7072b.png

    Площа =\(\frac{1}{2}\left(base\right)\left(height\right)=\frac{1}{2}\left(15\,\, m\right)\left(7\,\, m\right)=\frac{1}{2}\left(105\,\, m^2\right)=52.5\,\, m^2\)

    1. Трапеція висотою 5 футів і підставами 3 фути і 10 футів.

    clipboard_eec8892f4f9a1144e90dd070ea39ca2d2.png

    \(\begin{aligned}\text{Area} &= \frac{1}{2}(base\,\, 1+base\,\, 2)(height) \\ &= \frac{1}{2} (3\,\, ft+10\,\, ft)(5\,\, ft) \\ &= \frac{1}{2}(13\,\, ft)(5\,\, ft) \\ &= \frac{1}{2} \left(65\,\, ft^2\right)=32.5\,\, ft^2 \end{aligned} \)

    1. Обчисліть периметр і площу на наступному малюнку

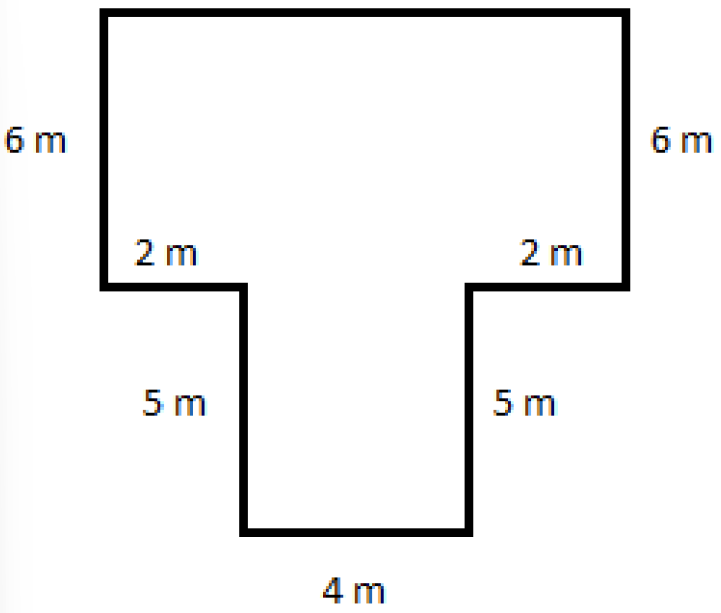
    clipboard_ef8097a296d8e904e7d812c8c0b4c76e1.png

    1. Обчисліть периметр.

    Оскільки периметр - це відстань навколо зовнішніх країв, то ми можемо обчислити відстань по верхньому краю, щоб бути сумою нижніх горизонтальних ребер, а саме\(2\,\, m\,\, +\,\, 4\,\, m\,\, +\,\, 2\,\, m\,\, =\,\, 8\,\, m\)

    Далі складаємо довжини зовнішніх країв для отримання

    \(\begin{aligned} \text{Perimeter} &=8\,\, m+6\,\, m+2\,\, m+5\,\, m+4\,\, m+5\,\, m+2\,\, m+6\,\, m \\ &= 8\,\, m+2\left(6\,\, m\right)+2\left(2\,\, m\right)+2 \left(5\,\, m\right)+4\,\, m \\ &=8\,\, m+12\,\, m+4\,\, m+10\,\, m+4\,\, m\\ &=38\,\, m\end{aligned}\)

    1. Обчисліть площу.

    Використовуючи пунктирну лінію, розділіть фігуру на два прямокутника, провівши горизонтальну лінію через фігуру на позначці 2 м

    clipboard_e03f2badf807e268b6dfc5684dec6f162.png

    Далі знайдіть площу кожної фігури і складіть результати, щоб отримати площу вихідної фігури.

    Площа верхнього прямокутника = A\({}_{1}\) =\(\left(6\,\, m\right)\left(8\,\, m\right)=48\,\, m^2\)

    Площа нижнього прямокутника = A\({}_{2}\) =\(\left(5\,\, m\right)\left(4\,\, m\right)=20\,\, m^2\)

    Загальна площа = A\({}_{1}\) + A\({}_{2}\) =\(48\,\, m^2+20\,\, m^2=68\,\, m^2\)

    1. Обчисліть периметр і площу малюнка нижче.

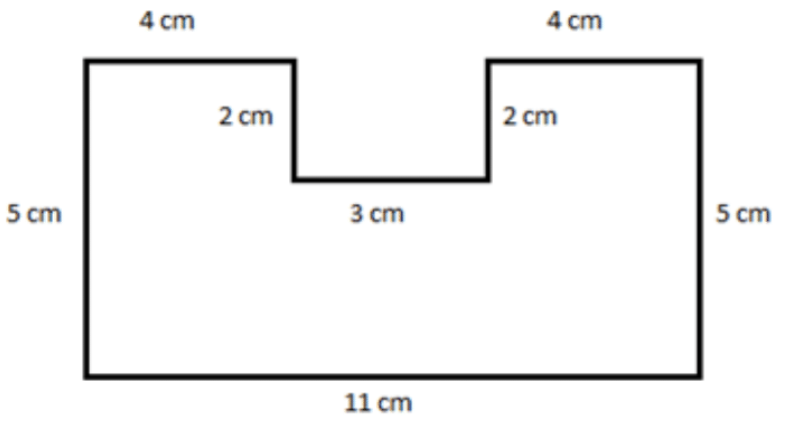
    clipboard_e3a0bc98baf654a531cca1adadd9d34c4.png

    1. Обчисліть периметр.

    Так як периметр - це відстань по зовнішніх краях, складаємо довжини країв для отримання

    \(\begin{aligned}\text{Perimeter} &= 4\,\, cm+2\,\, cm+3\,\, cm+2\,\, cm+4\,\, cm+5\,\, cm+11\,\, cm+5\,\, cm \\ &= 2\left(4\,\, cm\right)+2\left(2\,\, cm\right)+3\,\, cm+2\left(5\,\, cm\right)+11\,\, cm \\ &= 8\,\, cm+4\,\, cm+3\,\, cm+10\,\, cm+11\,\, cm\\ &=36\,\, cm\end{aligned} \)

    1. Обчисліть площу.

    Ми можемо обчислити площу цієї фігури одним із двох способів, або за допомогою додавання, або за допомогою віднімання. Давайте досліджуємо обидва методи.

    1. Використання додавання

    Розділіть фігуру на три прямокутника, провівши пунктирну лінію з лівого боку фігури через праву сторону фігури, з'єднавши на лінії 3 см.

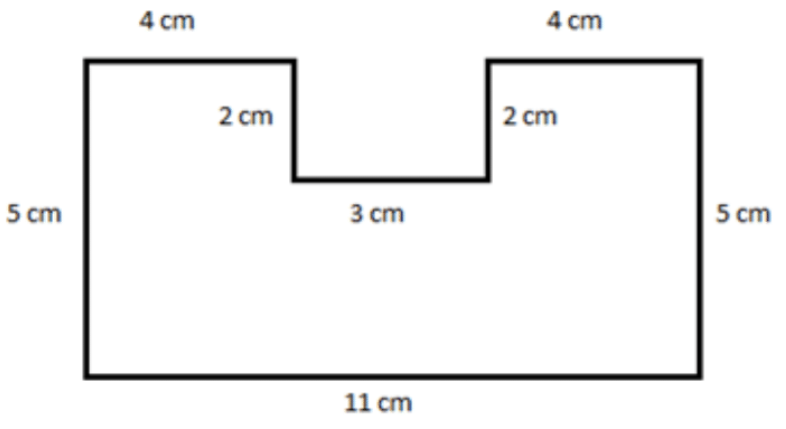
    clipboard_ebc9daa9f14fcf08ad2715aade5b659fa.png

    Обчисліть площу кожного прямокутника та додайте результати; звернемо увагу, що два верхніх прямокутника мають однаковий розмір

    Площа маленького прямокутника\(=\left(4\,\, cm\right)\left(2\,\, cm\right)=8\,\, cm^2\)

    Площа великого прямокутника\(=\left(3\,\, cm\right)\left(11\,\, cm\right)=33\,\, cm^2\)

    Загальна площа\(=8\,\, cm^2+8\,\, cm^2+33\,\, cm^2=49\,\, cm^2\)

    1. Використання віднімання

    Знайдіть площу зовнішнього прямокутника і відніміть площу прямокутного отвору, тому тепер проведемо горизонтальну пунктирну лінію поперек верхнього отвору фігури

    clipboard_eea981cf307c69a5efb5e2038ccae8e82.png

    Далі знайдемо площу більшого прямокутника зовнішнього краю

    Площа великого прямокутника\(=\left(5\,\, cm\right)\left(11\,\, cm\right)=55\,\, cm^2\)

    Площа прямокутного отвору\(=\left(2\,\, cm\right)\left(3\,\, cm\right)=6\,\, cm^2\)

    \(\begin{aligned} \text{Total Area} &= \text{Area of large outer rectangle – Area of the rectangular hole} \\ &=55\,\, cm^2-6\,\, cm^2=49\,\, cm^2\end{aligned} \)

    1. Прямокутний басейн вимірює 28 футів на 52 футів. Навколишній (і межує) басейн - це шлях шириною 3 фути. Знайдіть площу шляху.

    Для початку намалюємо фігуру, щоб зобразити сценарій. Почнемо з малювання прямокутника для представлення басейну.

    clipboard_ea49c2d18351ff38a6bdabd16cbd19e1b.png

    Далі, давайте намалюємо межу шириною 3 фути навколо басейну, щоб представити шлях. Контур представлений затіненою областю.

    clipboard_eda71fc97aabb35d0f5c7ac36c975b7ad.png

    Зовнішній край доріжки створює більший прямокутник, довжина якого дорівнює довжині басейну плюс подвійна ширина шляху або 52 фути + 2 (3 фути) = 58 футів. Ширина зовнішнього краю доріжки - ширина басейну плюс подвоєна ширина доріжки або 28 футів + 2 (3 фути) = 34 фути.

    Щоб отримати площу шляху, знайдіть

    площа зовнішнього краю - площа, огороджена басейном = площа доріжки

    \(\begin{aligned} \text{Area of the path} &= \left(58\,\, ft\right)\left(34\,\, ft\right)-(28\,\, ft)(52\,\, ft) \\ &=1972\,\, ft^2-1456\,\, ft^2\\ &=516\,\, ft^2 \end{aligned} \)

    1. Обчисліть бічну площу (площу поверхні) трикутної призми, як показано нижче

    clipboard_e2cd5180a63bedd199b897992db7a595f.png

    До цієї трикутної призми є п'ять сторін або поверхонь. Дві зі сторін трикутники однакового розміру, а саме з висотою 6 дюймів і основою 8 дюймів, а інші три сторони - прямокутники, ліве обличчя - прямокутник 6 дюймів на 7 дюймів, нижня грань - 8 дюймів на 7 дюймів прямокутник, а права сторона - 10 дюймів на 7 дюймів прямокутник.

    Щоб обчислити бічну площу або площу поверхні, знаходимо площу всіх поверхонь і додаємо результати

    Площа двох трикутників\(=2\left[\frac{1}{2}\left(8\,\, in\right)\left(6\,\, in\right)\right]=48\,\, in^2\)

    \(\begin{aligned}\text{Area of the three rectangles} &=\left(6\,\, in\right)\left(7\,\, in\right)+\left(8\,\, in\right)\left(7\,\, in\right)+\left(10\,\, in\right)\left(7\,\, in\right) \\ &=42\,\, in^2+56\,\, in^2+70\,\, in^2\\ &=168\,\, in^2\end{aligned} \)

    Бічна область\(=48\,\, in^2+168\,\, in^2=216\,\, in^2\)

    Більше прикладів використання об'ємних тривимірних об'єктів

    1. Розрахуйте об'єм прямокутної призми з розмірами 2 ярд X 6 ярдів X 7 ярдів.

    clipboard_ea4965ce5eff5a1081fcbff7d1dd1fada.png

    \[Volume=\left(length\right)\left(width\right)\left(height\right)=\left(2\,\, yds\right)\left(6\,\, yds\right)\left(7\,\, yds\right)=84\,\, yds^3\nonumber \]

    1. Обчисліть обсяг трикутної призми, як показано нижче.

    clipboard_e66ecf892ab7cb65e8a5f979185b71b4a.png

    \[V=\frac{1}{2}\left(base\right)\left(height\right)\left(depth\,\, or\,\, width\right) \nonumber \]

    \[V=\frac{1}{2}\left(8\,\, in\right)\left(6\,\, in\right)\left(7\,\, in\right)=168\,\, in^3 \nonumber \]

    1. Розрахуйте обсяг сфери діаметром 15,6 мм.

    \[V=\frac{2}{3}\left(0.785\right){\left(diameter\right)}^3=\frac{2}{3}\left(0.785\right){\left(15.6\,\, mm\right)}^3=\frac{2}{3}\left(0.785\right)\left(3796.416\,\, mm^3\right)=1986.8\,\, mm^3 \nonumber \]

    1. Обчисліть обсяг об'єкта нижче (не намальований в масштабі)

    clipboard_e07d9895431c87aa5005dc6cf4e0f0207.png

    \[\begin{aligned} \text{Total Volume} &=\text{Volume of the cylinder + Volume of the cone} \\ \text{Volume of cylinder} &=\left(0.785\right){\left(diameter\right)}^2\left(height\right) \\ &=\left(0.785\right){\left(2\,\, m\right)}^2\left(16\,\, m\right) \\ &= \left(0.785\right)\left(4\,\, m^2\right)\left(16\,\, m\right) \\ &=\left(0.785\right)\left(64\,\, m^3\right)\\ &=50.24\,\, m^3\end{aligned}\]

    \[\begin{aligned} \text{Volume of cone} &=\frac{1}{3}(0.785)\left(diameter\right)^2\left(height\right) \\ &= \frac{1}{3}\left(0.785\right)\left(2\,\, m\right)^2\left(3\,\, m\right)\\ &= \frac{1}{3} \left(0.785\right)\left(4\,\, m^2\right)\left(3\,\, m\right)\\ &=\frac{1}{3} \left(0.785\right)\left(12\,\, m^3\right)\\ &=3.14\,\, m^3\end{aligned} \]

    \[\begin{aligned} \text{Total Volume} &= \text{Volume of the cylinder + Volume of the cone}\\ &=50.24\,\, m^3+3.14\,\, m^3 \\ &=53.38\,\, m^3 \end{aligned} \]