4.2: Ламінарний потік вниз по похилій площині

У цьому розділі ми застосовуємо другий закон Ньютона для стійкого і рівномірного потоку вниз по похилій площині. Стратегія полягає в тому, щоб подивитися на блок потоку, обмежений уявними площинами, нормальними до дна, з одиницею ширини поперечного потоку і одиницею протяжності потоку (рис.\(\PageIndex{1}\)). У динаміці рідини такий блок рідини, як кажуть, є «вільним тілом». Оскільки потік вважається стійким і рівномірним, всі сили в потоковому напрямку, які чиниться на рідину у вільному тілі в будь-який момент часу, повинні складатися до нуля.

Слід зазначити спочатку, що поки я не буду звертатися до того, як влаштований потік так, щоб потік був рівномірним. Якщо ви просто виливаєте лист води на площину вздовж якоїсь певної горизонтальної лінії на площині, не слід очікувати, що рівномірний потік автоматично буде встановлений вниз по схилу цієї лінії в тому сенсі, що глибина потоку однакова на всіх нормальних ділянках, розташованих далі вниз по площині, і взагалі це не так: потрібно буде регулювати нахил площини для досягнення стану рівномірності. Це не банальна проблема, і її слід чекати деякого більш докладного матеріалу, далі в цьому розділі, про опір потоку. З іншого боку, це повинно мати інтуїтивний сенс для вас, що якщо площина дуже довга ступінь нерівномірності буде дуже маленькою незалежно від нахилу: просто уявіть, що ллєте воду з ряду маленьких кранів на площину довжиною милю і нахилом на кілька градусів.

Очевидно, що тільки рідини, а не гази, можуть протікати як потоки з відкритим каналом. Вільно деформується верхня поверхня рідини, звана вільною поверхнею, відкрита для повітря. Ми будемо нехтувати незначними силами, що чиниться вищестоящим повітрям на рухому рідину. Наш ідеалізований потік каналів має нескінченну ширину, без бічних меж, і тому це просто зручна абстракція. А ось потік в каналі прямокутного перерізу з шириною потоку набагато більшою за глибину потоку є хорошим наближенням до потоку з нескінченною шириною.

Візьміть\(x\) напрямок вниз за течією, а напрямок y - нормальним до межі, з\(y = 0\) внизу потоку (рис. 4-1). За умови нековзання швидкість дорівнює нулю при\(y = 0\), тому швидкість повинна збільшуватися вгору в потоці. Зрозуміло також, що потік всюди спрямований прямо вниз по площині. Подумайте про сили, що діють на рідину, що міститься в даний момент у вільному тілі в межах прямокутного об'єму, утвореного вільною поверхнею, нижньою межею і двома парами уявних площин, нормальних до дна і з одиничним інтервалом, одна пара паралельна потоку і віднесена на відстань\(B\) один від одного, а інший нормальний до потоку і віддалений на відстані\(L\) один від одного (рис.\(\PageIndex{1}\)).

Рисунок\(\PageIndex{1}\): Ескіз визначення для отримання граничного напруження зсуву в стійкому рівномірному потоці вниз по похилій площині.

Написання другого закону Ньютона для балансу сил на цьому вільному тілі означає прирівнювання рушійної сили вниз нахилу, викликаної спадної складової ваги рідини у вільному тілі, з силою опору, що чиниться плоской межею на нижній поверхні вільного тіла. Вага рідини у вільному тілі дорівнює\(\gamma B L d\), де\(d\) знаходиться глибина течії. Схил складовою цієї ваги є\(\gamma \sin \alpha B L d\), де\(\alpha\) кут нахилу площини (рис.\(\PageIndex{2}\)).

Малюнок\(\PageIndex{2}\): Сили на вільному тілі рідини в стійкому рівномірному потоці вниз по похилій площині.

Це врівноважується силою тертя, що\(\tau_{\text{o}} B L\) чиниться нижньою межею. Існують також сили тиску, що діють паралельно напрямку потоку на верхніх і нижніх гранях вільного тіла, але оскільки, за нашим припущенням рівномірності, вертикальний розподіл цих сил тиску однаковий на кожному поперечному перерізі, вони врівноважують один одного і не викликають чистої сили на вільне тіло. Встановлення\(\gamma \sin \alpha B L d\) рівних\(\tau_{\text{o}} B L\) і рішення для\(\tau_{\text{o}}\),

\[\tau_{\text{o}}=\gamma d \sin \alpha \label{4.1} \]

тому граничне напруження зсуву прямо пропорційно добутку глибини потоку, питомої ваги рідини та синусу кута нахилу.

Малюнок\(\PageIndex{3}\): Ескіз прямокутного відкритого каналу шириною b, щоб допомогти у визначенні гідравлічного радіуса.

Перш ніж продовжити розвиток, зробимо рівняння опору більш актуальним для реального світу, написавши аналогічне рівняння для каналу з прямокутним перетином, а потім для каналу з довільним (але незмінним) перетином. Щоб узагальнити Equation\ ref {4.1} до прямокутного каналу, візьміть ширину потоку\(b\) (рис.\(\PageIndex{3}\)) і запишіть баланс сили для вільного тіла, яке заповнює канал, від стіни до стіни, в відрізку довжини\(L\) вздовж потоку. Виконання тієї ж математики, що і вище, дає результат.

\[\tau_{o}=\gamma \sin \alpha \frac{b d}{2 d+b} \label{4.2} \]

Малюнок\(\PageIndex{4}\): Змочений периметр прямого потоку відкритого каналу.

Для узагальнення рівняння\ ref {4.1} до каналу довільної форми поперечного перерізу припустимо, що площа поперечного перерізу дорівнює\(A\) і змочений периметр (відстань по зануреної частини кордону від ватерлінії до ватерлінії) дорівнює\(P\) (рис.\(\PageIndex{4}\)). Такий же баланс сил дає

\[\tau_{\text{o}}=\gamma \sin \alpha \frac{A}{P} \label{4.3} \]

Рівняння\ ref {4.1},\ ref {4.2}, і\ ref {4.3} виглядають досить інакше, але їх легко уніфікувати, визначивши величину, звану гідравлічним радіусом,\(R_{H}\) утвореним діленням площі поперечного перерізу потоку на змочений периметр. Ви можете самі переконатися в тому, що гідравлічний радіус потоку в прямокутному каналі є\(b d /(2 d+b)\). Трохи складніше помітити, що гідравлічний радіус нескінченно широкого канального потоку - це всього лише глибина потоку\(d\). Ви можете міркувати\(d\), що у міру\(b\) збільшення ширини щодо глибини термін\(2d\) у знаменнику\(2d+b\) стає меншою і меншою частиною знаменника, тому гідравлічний радіус\(bd/(2d+b)\) прагне до\(bd/b\), або просто\(d\), як ширина збільшується відносно на глибину. Права частина всіх трьох рівнянь,\ ref {4.1},\ ref {4.2} і\ ref {4.3}, стають\(\gamma \sin \alpha R_{H}\).

Рівняння\ ref {4.3}, або його окремі випадки Equation\ ref {4.1} або Equation\ ref {4.2}, є основним рівнянням опору для стійкого рівномірного потоку у відкритому каналі. Не так багато корисних результатів у механіці рідини так легко отримати! Це основний спосіб виявлення граничного напруження зсуву в річках (хоча, щоб використовувати його таким чином, вам потрібно зробити деякі зйомки, щоб встановити висоту поверхні води в двох точках уздовж русла, принаймні сотні, якщо не тисячі метрів один від одного). Іноді три рівняння записуються через ухил\(\tan \alpha\), а не синус кута нахилу\(\sin \alpha\), тому що для дуже малих\(\alpha\) (звичайний випадок) наближення\(\sin \alpha \approx \tan \alpha\) є хорошим.

Тепер повернемося до нескінченно широкого потоку вниз по площині: тепер, коли ви знаєте, як знайти граничне напруження зсуву, що можна сказати про те, як напруга зсуву і швидкість потоку в потоці змінюються залежно від висоти над дном? Одне ви вже точно знаєте: за умовою нековзання швидкість в самому низу повинна дорівнювати нулю. Інша річ, яку можна сказати без подальшого виведення, це те, що швидкість повинна бути на максимумі на вільній поверхні. Чому? Оскільки рушійна сила тяжіння вниз нахилу - це «сила тіла», яка діє протягом усього потоку, тоді як сила опору тертя діє лише внизу. Тому швидкість потоку повинна монотонно збільшуватися вгору в потоці.

Рисунок\(\PageIndex{5}\): Ескіз визначення для отримання розподілу напруги зсуву в стійкому рівномірному ламінарному потоці з відкритим каналом.

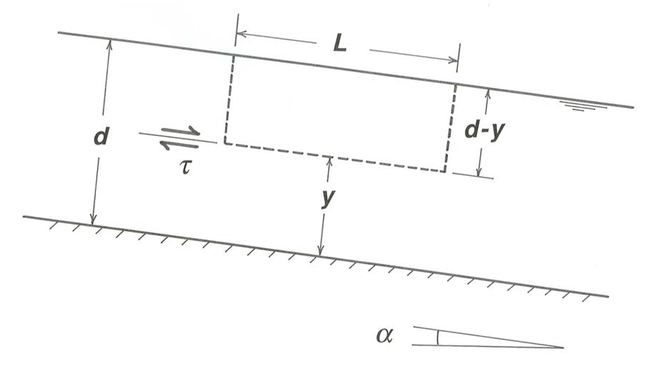
Ми можемо знайти напругу зсуву та швидкість у всіх точках вгору в потоці, застосувавши ту саму процедуру балансування сили до вільного тіла рідини, подібного до тієї, що використовується вище, але з її нижньою гранню, утвореною уявною площиною на змінну відстань\(y\) над дном і паралельно їй (рис.\(\PageIndex{5}\)). Напруга зсуву\(\tau\) по площині задається безпосередньо силовим балансом:

\[\tau=\gamma \sin \alpha(d-y) \label{4.4} \]

Використовуючи Equation\ ref {4.1} для усунення\(\gamma \sin \alpha\) з рівняння\ ref {4.4}, ми можемо записати\(\tau\) через граничне напруження зсуву\(\tau_{\text{o}}\):

\[\tau=\tau_{\text{o}}\left(1-\frac{y}{d}\right) \label{4.5} \]

Рівняння\ ref {4.5} показує, що лінійно\(\tau\) змінюється від максимуму внизу до нуля на поверхні (рис. 4-6).\(\gamma \sin \alpha\)

Малюнок\(\PageIndex{6}\): Розподіл напруги зсуву в стійкому рівномірному ламінарному потоці з відкритим каналом. (Пізніше в тексті зазначається, що цей розподіл також стосується турбулентного потоку.)

Виключення\(\tau\) з рівняння\ ref {4.4} за допомогою Рівняння 1.3.6 дає вираз для градієнта швидкості\(du/dy\):

\(\mu \frac{d u}{d y}=\gamma \sin \alpha(d-y)\)

\[\frac{d u}{d y}=\frac{\gamma \sin \alpha}{\mu}(d-y) \label{4.6} \]

Рівняння\ ref {4.6} може бути інтегровано для отримання розподілу швидкості від нижньої межі до вільної поверхні:

\(\begin{aligned} u &=\int \frac{d u}{d y} d y \\ &=\int \frac{\gamma \sin \alpha}{\mu}(d-y) d y \\ &=\frac{\gamma \sin \alpha}{\mu}\left(d \int d y+\int y d y\right) \\ &=\frac{\gamma \sin \alpha}{\mu}\left(y d+\frac{1}{2} y^{2}\right)+c \end{aligned}\)

Ми можемо оцінити константу інтеграції\(c\) за допомогою граничної умови, що\(u = 0\) в\(y = 0\); ми знаходимо\(c = 0\), що, так

\[u=\frac{\gamma \sin \alpha}{\mu}\left(y d+\frac{1}{2} y^{2}\right) \label{4.7} \]

Для заданих значень\(\gamma\)\(\alpha\),\(\mu\), і\(d\), швидкість\(u\) таким чином змінюється параболічно від нуля на нижній межі до максимуму на поверхні (рис.\(\PageIndex{7}\)). З іншого боку, від Equation\ ref {4.7} градієнт швидкості\(du/dy\) змінюється лінійно від максимуму внизу до нуля на вільній поверхні, оскільки він прямо пропорційний напруженню зсуву (рис.\(\PageIndex{7}\)).

Рисунок\(\PageIndex{7}\): Вертикальний розподіл швидкості, напруги зсуву та градієнта швидкості в стійкому рівномірному ламінарному потоці з відкритим каналом.

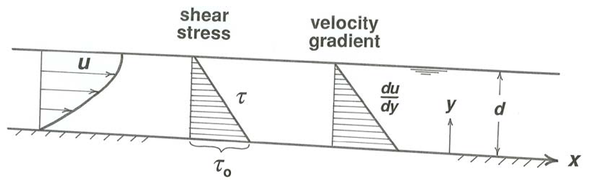
Ось нагадування про зсув всередині текучої рідини, з яким ви вперше зіткнулися ще в главі 1. Ви можете думати, вільно, з точки зору шарів рідини, що ковзають один за одним. Хороший спосіб зробити цей бетон - отримати дуже товсту телефонну книгу та «стійку» її сторінки, міцно поклавши руки на передню та задню обкладинки та ковзаючи їх паралельно один одному у напрямку, перпендикулярному хребту книги. У рідинях, звичайно, зсув є безперервним, а не у вигляді дискретних шарів.