2: Ваги та перетворення
- Page ID
- 36855
Ваги та трансформації
Девід ДіБіаз
2.1. Огляд
Глава 1 окреслила кілька відмінних властивостей географічних даних. Один з них полягає в тому, що географічні дані обов'язково узагальнюються, і що узагальнення має тенденцію змінюватися залежно від масштабу. Друга відмінна властивість полягає в тому, що складна, майже сферична форма Землі ускладнює зусилля по визначенню точних положень на поверхні Землі. У цьому розділі досліджуються наслідки цих властивостей шляхом висвітлення концепцій масштабу, геометрії Землі, систем координат, «горизонтальних датумів», які визначають взаємозв'язок між системами координат та формою Землі, а також різні методи перетворення координатних даних між 3D та 2D сітками, і від однієї бази до іншої.
Порівняно з главою 1, глава 2 може здатися довгою, технічною та абстрактною, особливо тим, для кого ці поняття є новими. Зареєстровані студенти помітять, що ми виділили більше часу для роботи над главою та пов'язаними з ними вікторинами. Сім практичних вікторин доступні в ANGEL, щоб допомогти зареєстрованим студентам отримати контроль над цими поняттями. Глава 2 також включає оцінену вікторину в тому ж форматі відкритої книги, що і практичні вікторини. Якщо ви робите досить добре на практиці вікторини, ви повинні зробити досить добре на градуйованому вікторині теж.
Цілі
Студенти, які успішно завершили главу 2, повинні мати можливість:
- Продемонструйте свою здатність вказувати геопросторові місця розташування за допомогою географічних координат;
- Перетворення географічних координат між двома різними форматами;
- Пояснити поняття горизонтальної бази;
- Обчислити зміну координатного розташування внаслідок зміни з однієї горизонтальної бази на іншу;
- Оцініть величину «зсуву бази», пов'язаного з коригуванням від NAD 27 до NAD 83;
- Визнати вид перетворення, який підходить для геореєстрації двох або більше наборів даних;
- Опишіть характеристики системи координат UTM, включаючи її основу в проекції поперечної карти Меркатора;
- Ділянка координат UTM на карті;
- Охарактеризуйте характеристики системи SPC, включаючи картографічну проекцію, на якій вона заснована;
- Перетворення географічних координат в координати SPC;
- Інтерпретувати діаграми спотворень для виявлення геометричних властивостей сфери, які зберігаються певною проекцією; і
- Класифікуйте проектовані решітки за сімейством проекцій.
Коментарі та запитання
Зареєстровані студенти можуть залишати коментарі, запитання та відповіді на запитання щодо тексту. Особливо вітаються анекдоти, які пов'язують текст глави з вашим особистим або професійним досвідом. Крім того, в системі управління курсами ANGEL доступні дискусійні форуми для коментарів і питань на теми, якими ви, можливо, не захочете ділитися з усім світом.
Щоб залишити коментар, прокрутіть вниз до текстового поля під «Опублікувати новий коментар» і почніть вводити текст у текстовому полі, або ви можете відповісти на існуючу гілку. Коли ви закінчите вводити текст, натисніть кнопку «Попередній перегляд» або «Зберегти» (Зберегти фактично надішле ваш коментар). Після того, як ваш коментар буде опублікований, ви зможете редагувати або видаляти його за потребою. Крім того, ви зможете відповісти на інші публікації в будь-який час.
Примітка: перші кілька слів кожного коментаря стають його «заголовком» у гілці.
2.2. Контрольний список
Наступний контрольний список призначений для студентів штату Пенн, які зареєстровані для класів, в яких цей текст, і пов'язані вікторини та проекти в системі управління курсами ANGEL були призначені. Можливо, вам буде корисно спочатку роздрукувати цю сторінку, щоб ви могли слідувати інструкціям.
| Крок | Діяльність | Доступ/Напрямки |
|---|---|---|
| 1 | Читати главу 2 | Це друга сторінка глави. Натисніть на посилання внизу сторінки, щоб продовжити або повернутися до попередньої сторінки, або перейти до верхньої частини глави. Ви також можете переміщатися по тексту за посиланнями в меню GEOG 482 зліва. |
| 2 | Надішліть вісім практичних вікторин, включаючи:
| Перейдіть до ANGEL> [розділ курсу] > вкладка Уроки > Розділ 2 папка > [вікторина] |
| 3 | Виконайте дії «Спробуйте це» У тому числі:
| Інструкції надаються для кожного виду діяльності. |
| 4 | Надішліть главу 2 градуйовану вікторину | ANGEL > [розділ вашого курсу] > вкладка Уроки > Розділ 2 папка > Розділ 2 градуйована вікторина |
| 5 | Читайте коментарі та запитання, розміщені однокурсниками. Додавайте свої коментарі та питання, якщо такі є. | Коментарі та питання можуть бути розміщені на будь-якій сторінці тексту або на дискусійному форумі, присвяченому главі в ANGEL. |
2.3. Масштаб
Зокрема, у цій частині глави 2 ви навчитеся:
- Обчислити масштаб карти за допомогою представницьких дробів.
- Опишіть загальний зв'язок між масштабом карти, деталізацією та точністю.
2.4. Масштабування як область
Часто «масштаб» використовується як синонім «сфера дії» або «ступінь». Наприклад, назва міжнародного дослідницького проекту під назвою Великий масштабний експеримент з біосфери та атмосфери в Амазонії (1999) використовує термін «великий масштаб» для опису всебічного дослідження екологічних систем, що працюють у великому регіоні. Таке використання поширене не лише серед екологів та активістів, а й серед економістів, політиків та преси. Ті з нас, хто спеціалізується на географічній інформації, зазвичай використовують слово «масштаб» по-різному, однак.
2.5. Масштаб карт і фотографій
Коли люди, які працюють з картами та аерознімками, використовують слово «масштаб», вони зазвичай говорять про розміри речей, які з'являються на карті або повітряній фотографії, щодо фактичних розмірів цих речей на землі.
Масштаб карти - це пропорція між відстанню на карті та відповідною відстанню на землі:
(Dm/Dg).
За умовністю пропорція виражається як «представницький дріб», в якому відстань карти (Dm) зменшується до 1. Пропорція, або співвідношення, також зазвичай виражається у вигляді 1: Dg, а не 1/Dg.
Представницька фракція 1:100 000, наприклад, означає, що ділянка дороги, яка вимірює 1 одиницю довжини на карті, означає ділянку дороги на землі довжиною 100 000 одиниць.
Якби ми змінили масштаб карти таким чином, щоб довжина ділянки дороги на карті була зменшена, скажімо, до 0,1 одиниці довжини, ми б створили карту меншого масштабу, представницька частка якої дорівнює 0. 1:100 000, або 1:1 000 000. Коли ми говоримо про великомасштабних і дрібномасштабних картах і географічних даних, то мова йде про відносні розміри і рівні деталізації ознак, представлених в даних. Загалом, чим більше масштаб карти, тим детальніше показано. Ця тенденція проілюстрована нижче.
Географічні дані узагальнюються за масштабом. Натисніть на кнопки під картою, щоб збільшити і зменшити масштаб міста Gorham. (Адаптовано з Томпсона, 1988)
Однією з визначальних характеристик топографічних карт є те, що масштаб узгоджений на кожній карті та в межах кожної серії карт. Це не стосується аерофотознімків, однак, за винятком зображень, які були орторектифіковані. Як обговорювалося в розділі 6, великі масштабні карти, як правило, отримані з аерофотознімків. Однією з проблем, пов'язаних з використанням повітряних фотографій як джерел даних карти, є те, що масштаб повітряного зображення змінюється від місця до місця в залежності від висоти місцевості, показаної на сцені. Якщо припустити, що літак, що несе камеру, підтримує постійну висоту польоту (що пілоти таких літаків дуже стараються зробити), відстань між камерою і землею змінюється по кожній траєкторії польоту. Це призводить до того, що масштаб фотографій повітря буде більшим там, де місцевість вище і менше, де рельєф нижче. «Орторектіфіковане» зображення - це зображення, в якому зміни масштабу, спричинені варіаціями висоти місцевості (серед інших ефектів), були видалені.
Розрахувати середню шкалу невиправленої повітряної фотографії можна, вирішивши рівняння Sp = f/(H-havG), де f - фокусна відстань камери, H - висота польоту літака над середнім рівнем моря, а havg - середня висота місцевості. Також можна обчислити повітряну фотошкалу в конкретній точці, вирішивши рівняння Sp = f/(H-h), де f - фокусна відстань камери, H - висота польоту літака над середнім рівнем моря, а h - висота місцевості в заданій точці. Ви будете мати можливість практикувати обчислення як масштабу карти, так і масштабу повітряних фотографій у майбутній практичній вікторині.
2.6. Ваги графічної карти
Інший спосіб виразити масштаб карти - це графічний (або «смуговий») масштаб. На відміну від репрезентативних дробів, графічні масштаби залишаються істинними, коли карти скорочуються або збільшуються.
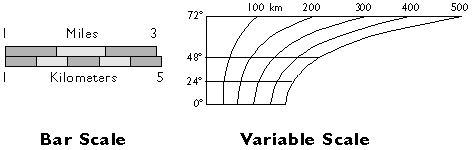
Графічні шкали.
Якщо вони включають масштаб взагалі, більшість карт містять шкалу смужок, подібну до показаної вище ліворуч. Деякі також виражають масштаб карти як репрезентативний дріб. У будь-якому випадку, мається на увазі, що масштаб рівномірний по всій карті. Насправді, за винятком карт, які показують лише дуже малі області, масштаб змінюється на кожній карті. Як ви, напевно, знаєте, це випливає з того, що положення на майже сферичної Землі необхідно трансформувати в положення на двовимірних аркушах паперу. Систематичні перетворення такого роду називаються картографічними проекціями. Як ми поговоримо більш глибоко пізніше в цьому розділі, всі проекції карти супроводжуються деформацією об'єктів у деяких або всіх областях карти. Ця деформація призводить до того, що масштаб карти змінюється на карті. Тому представницькі дроби можуть вказувати масштаб карти вздовж лінії, при якій деформація мінімальна (номінальна шкала). Барні шкали позначають тільки номінальну або середню шкалу карти. Змінні масштаби, як показано вище праворуч, показують, як масштаб змінюється, в даному випадку за широтою, через деформацію, спричинену проекцією карти.
2.7. Масштаб карти і точність
Однією з особливостей географічних даних є те, що явища, показані на картах, як правило, представлені по-різному в різних масштабах. Як правило, у міру зменшення масштабу теж зростає кількість різних ознак, і деталізація, з якою вони представлені. Не тільки друковані карти, але й цифрові набори географічних даних, які охоплюють великі області, як правило, більш узагальнені, ніж набори даних, які охоплюють обмежені області.
Точність також має тенденцію змінюватися пропорційно масштабу карти. Геологічна служба Сполучених Штатів, наприклад, гарантує, що відображені позиції 90 відсотків чітко визначених точок, показаних на серії топографічних карт, у масштабах менше 1:20 ,000, будуть знаходитися в межах 0,02 дюйма від їх фактичного положення на карті (див. Національні стандарти геопросторової програми) та Технічні характеристики). Зверніть увагу, що цей «Національний стандарт точності карт» залежить від масштабу. Допустима похибка чітко визначених точок (таких як контрольні точки, перехрестя доріг тощо) на топографічних картах масштабу 1:250 000, таким чином, становить 1/250,000 = 0,02 дюйма/Dg або Dg = 0,02 дюйма х 250 000 = 5000 дюймів або 416,67 футів. Ні малі карти, ні цифрові дані, отримані з них, не є надійними джерелами детальної географічної інформації.
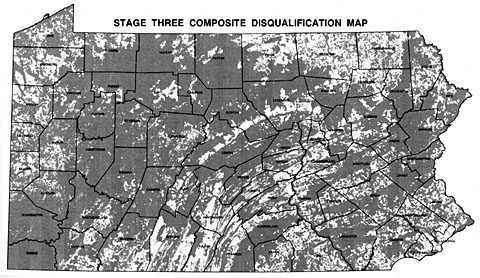
Райони (сірим кольором) дискваліфіковані як потенційні місця для зберігання радіоактивних відходів низького рівня, зображені на малій карті масштабу (оригінал 1:1,500,000) маскують невеликі придатні райони, досить великі, щоб містити об'єкт площею 500 акрів (Chem-Nuclear Systems, Inc., 1994).
Іноді втрачена на дрібномасштабних картах деталізація викликає серйозні проблеми. Наприклад, підрядник, найнятий для використання ГІС, щоб знайти підходящу ділянку для зберігання радіоактивних відходів низького рівня в Пенсільванії, представив серію карт масштабу 1:1,500,000 на громадських слуханнях навколо штату на початку 1990-х років. Масштаб був обраний таким чином, щоб дискваліфіковані ділянки всієї держави могли бути надруковані на одній сторінці 11 х 17 дюймів. Звіт, що супроводжує карту, включав відмову від відповідальності, що «можливо, що невеликі площі достатнього розміру для об'єкта захоронення LLRW можуть існувати в регіонах, які здаються дискваліфікованими на [карті]. Детальна інформація для цих невеликих районів зберігається в ГІС, хоча вони візуально не ілюстровані...» (Chem-Nuclear Systems, Inc. 1993, стор. 20). На жаль для підрядника, оповіщення громадяни визнали недоліки маломасштабної карти, а газети опублікували повідомлення, звинувачуючи позадержавну компанію в наданні недостовірних документів. Наступні карти були виготовлені в досить великому масштабі, щоб розрізнити придатні райони площею 500 акрів.
2.8. Масштаб як дієслово
Термін «шкала» іноді вживається як дієслово. Масштабувати карту - це відтворити її в іншому розмірі. Наприклад, якщо ви фотографічно зменшите карту масштабу 1:100 000 до 50 відсотків від її початкової ширини та висоти, результат буде на чверть площі оригіналу. Очевидно, масштаб карти зменшення також був би меншим: 1/2 х 1/100,000 = 1/200,000.
Через неточності, властиві всім географічним даними, особливо в маломасштабних картах, скрупульозні фахівці з географічної інформації уникають збільшення вихідних карт. Для цього потрібно перебільшувати узагальнення та помилки. Оригінальна карта, яка використовується для ілюстрації районів у Пенсільванії, дискваліфікована з розгляду для зберігання радіоактивних відходів низького рівня, показана на попередній сторінці, наприклад, була надрукована із заявою: «Через масштаб карти та міркування друку не доцільно збільшувати або іншим чином покращувати особливості на цій карті.»
ПРАКТИКА ВІКТОРИНИ
Зареєстровані студенти штату Пенн повинні повернутися зараз до папки Глава 2 в ANGEL (через меню Ресурси ліворуч), щоб пройти самооцінку вікторини про Масштаб карти.
Ви можете приймати практичні вікторини стільки разів, скільки хочете. Вони не забиваються і ніяк не впливають на вашу оцінку.
2.9. Ваги геопросторових вимірювань
Слово «масштаб» також може використовуватися як синонім лінійки - шкала вимірювань. Оскільки дані складаються з символів, які представляють вимірювання явищ, важливо зрозуміти еталонні системи, що використовуються для проведення вимірювань в першу чергу. У цьому розділі ми розглянемо масштаб вимірювань, відомий як географічна система координат, яка використовується для визначення позицій на приблизно сферичній поверхні Землі. В інших розділах ми зустрінемо двовимірні (плоскі) системи координат, а також шкали вимірювань, які використовуються для вказівки даних атрибутів.
У цьому розділі глави 2 ви:
- Продемонструйте свою здатність вказувати геопросторові місця за допомогою географічних координат.
- Перетворення географічних координат між двома різними форматами.
2.10. Системи координат
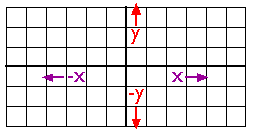
Декартова система координат.
Як ви, напевно, знаєте, місця на поверхні Землі вимірюються і представляються в терміні координат. Координата - це набір з двох або більше чисел, який визначає положення точки, лінії або іншої геометричної фігури по відношенню до якоїсь системи відліку. Найпростіша система такого роду - декартова система координат (названа на честь математика і філософа 17 століття Рене Декарта). Декартова система координат - це просто сітка, утворена шляхом зіставлення двох шкал вимірювання, однієї горизонтальної (x) та однієї вертикальної (y). Точка, в якій і x і y дорівнюють нулю, називається початком системи координат. На ілюстрації вище початок (0,0) знаходиться в центрі сітки. Всі інші позиції вказуються щодо походження. Координата верхнього правого кута сітки дорівнює (6,3). Нижній лівий кут - (-6, -3). Якщо це не зрозуміло, будь ласка, зверніться за роз'ясненнями!
Декартові та інші двовимірні (плоскі) системи координат зручні завдяки своїй простоті. Однак зі зрозумілих причин вони не ідеально підходять для визначення геопросторових позицій. Географічна система координат розроблена спеціально для визначення положень на шорстко-сферичній поверхні Землі. Замість двох лінійних шкал вимірювання x і y географічні системи координат зіставляють дві криволінійні шкали вимірювань. Шкала схід-захід, звана довготою (умовно позначається грецьким символом лямбда), коливається від +180° до -180°. Оскільки Земля кругла, +180° (або 180° E) та -180° (або 180° W) є однією лінією сітки. Ця лінія сітки є приблизно Міжнародною лінією дати, яка має диверсії, які проходять навколо деяких територій та острівних груп. Навпроти Міжнародної лінії дат знаходиться основний меридіан, лінія довготи, визначена міжнародним договором як 0°. Шкала північ-південь, яка називається широтою (позначена грецьким символом phi), коливається від +90° (або 90° с.ш.) на північному полюсі до -90° (або 90° S) на Південному полюсі. Далі ми розглянемо географічну систему координат.
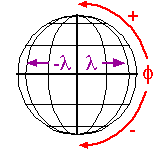
Географічна (або «геодезична») система координат.
2.11. Географічна система координат
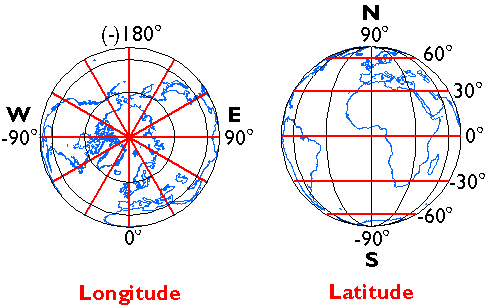
Географічна система координат.
Довгота визначає позиції на схід та захід як кут між простим меридіаном та другим меридіаном, який перетинає точку інтересу. Довгота коливається від +180 (або 180° E) до -180° (або 180° W). 180° східної та західної довготи разом утворюють міжнародну лінію дати.
Широта визначає позиції на північ і південь з точки зору кута, піднесеного в центрі Землі між двома уявними лініями, однією, яка перетинає екватор, а інша, яка перетинає точку інтересу. Широта коливається від +90° (або 90° с.ш.) на північному полюсі до -90° (або 90° S) на Південному полюсі. Лінія широти також відома як паралель.
У більш високих широтах довжина паралелей зменшується до нуля на 90° півночі та півдня. Лінії довготи не паралельні, а сходяться до полюсів. Таким чином, хоча ступінь довготи на екваторі дорівнює відстані близько 111 кілометрів, ця відстань зменшується до нуля на полюсах.
СПРОБУЙ ЦЕ!
ЗАСТОСУВАННЯ ПРАКТИКИ ГЕОГРАФІЧНОЇ СИСТЕМИ КООРДИНАТ
Майже всі вивчали широту і довготу в дитинстві. Але наскільки добре ви розумієте географічну систему координат, насправді? Мій досвід полягає в тому, що в той час як кожен, хто входить в цей клас, чув про широту і довготу, лише близько половини може вказати на місце розташування на карті, яке визначається парою географічних координат. Додаток Flash, пов'язане нижче, дозволяє перевірити свої знання. Додаток просить вас натиснути місця на глобусі, як зазначено випадково згенерованими географічними координатами.
Ви помітите, що програма дозволяє вибирати між «легкими проблемами» і «важкими проблемами». Легкими задачами є ті, в яких координати широти і довготи задаються з кроком 30°. Оскільки роздільна здатність решітки (сітки географічної системи координат), що використовується в додатку, також становить 30°, рішення кожної «легкої» проблеми відбувається на перетині паралелі та меридіана. До «легких» проблем відносяться хороші розминки.
«Жорсткі» задачі визначають координати з кроком 1°. Ви повинні інтерполювати позиції між лініями сітки. Ви можете вважати себе хорошими робочими знаннями географічної системи координат, якщо ви зможете вирішити принаймні шість «важких» завдань послідовно та за першим клацанням миші.
Натисніть тут, щоб завантажити та запустити програму практики Географічна система координат (5.7 Мб). (Якщо глобус не відображається після завантаження програми Flash, клацніть правою кнопкою миші та виберіть «Відтворити» у спливаючому меню.)
Примітка. Щоб виконати цю вправу, вам потрібно буде встановити програвач Adobe Flash. Якщо у вас ще немає Flash player, ви можете завантажити його безкоштовно на сайті adobe.
2.12. Формати географічних координат
Географічні координати можуть бути виражені в десяткових градусах або в градусах, хвилинах і секундах. Іноді потрібно конвертувати з однієї форми в іншу. Стів Кіуттіс (особисте спілкування, весна 2002), менеджер Пенсільванської програми пошуку та порятунку міст, описав одну таку ситуацію на дошці оголошень курсу: «Мені довелося бути в державному центрі надзвичайних операцій в Гаррісбурзі в середу ввечері, коли надійшов дзвінок з рятувальних військово-повітряних сил Координаційний центр в Дуврі, DE. Вони мали активацію передавача аварійного локатора (ELT) і попросили цивільного повітряного патруля ПА провести розслідування. Координати, дані офіцеру, були 39 52,5 п і -75 15.5 w Це було побудовано неправильно (розглянуто так, ніби координати були в десяткових градусах 39.525n і -75.155 w), і місцезнаходження виявилося поблизу Vineland, Нью-Джерсі. Я зрозумів, що це повинно було бути інтерпретовано як 39 градусів 52 хвилини і 5 секунд п і -75 градусів і 15 хвилин і 5 секунд w) і зробив перетворення (як нас вчили в розділі 2) і придумав місце розташування на території міжнародного аеропорту Філадельфії, де був знайдений локатор, в припаркованому авіалайнері».
Ось як це працює:
Щоб перетворити -89.40062 з десяткових градусів в градуси, хвилини, секунди:
- Відніміть кількість цілих градусів (89°) від загальної кількості (89.40062°). (Знак мінус використовується у форматі десяткового ступеня лише для того, щоб вказати, що значенням є західна довгота або південна широта.)
- Помножте залишок на 60 хвилин (0,40062 х 60 = 24,0372).
- Відніміть кількість цілих хвилин (24 ′) з продукту.
- Помножте залишок на 60 секунд (.0372 x 60 = 2.232).
- Результатом є 89° 24 ′ 2,232 ″ Ш або S.
Щоб перетворити 43° 4 ′ 31″ від градусів, хвилин, секунд до десяткових градусів:
DD = Градуси + (хвилин/60) + (секунди/3600)
- Розділіть кількість секунд на 60 (31 ÷ 60 = 0,5166).
- Додайте частку кроку (1) до цілої кількості хвилин (4 + 0,5166).
- Розділіть результат кроку (2) на 60 (4,5166 ÷ 60 = 0,0753).
- Додайте частку кроку (3) до кількості цілих числових ступенів (43 + 0,0753).
- Результат - 43.0753°
ПРАКТИКА ВІКТОРИНИ
Зареєстровані студенти штату Пенн повинні повернутися зараз до папки Глава 2 в ANGEL (через меню Ресурси ліворуч), щоб пройти тест самооцінки про Географічну систему координат.
Ви можете приймати практичні вікторини стільки разів, скільки хочете. Вони не забиваються і ніяк не впливають на вашу оцінку.
2.13. Горизонтальні датуми
Географічні дані представляють розташування та атрибути речей на поверхні Землі. Місця вимірюються та кодуються з точки зору географічних координат (тобто широти та довготи) або координат площини (наприклад, UTM). Щоб точно виміряти і задати координати, спочатку потрібно визначити геометрію самої поверхні. Щоб зрозуміти, що я маю на увазі, уявіть футбольний м'яч. Якщо ви або ваші діти грають у футбол, ви, ймовірно, можете викликати бачення круглої мозаїки 20 гексагональних (шість сторонніх) і 12 п'ятикутних (п'ятисторонніх) панелей (футбольні м'ячі бувають різних конструкцій, але 32-панельний м'яч використовується в більшості професійних матчів. Відвідайте soccerballworld.com більше, ніж ви коли-небудь хотіли знати про футбольні м'ячі). Тепер зосередьтеся на одній точці на перетині трьох панелей. Ви можете використовувати сферичні (наприклад, географічні) координати, щоб вказати положення цієї точки. Але якщо ви здуваєте кульку, положення точки в просторі змінюється, і так повинні його координати. Абсолютне (хоча і не відносне) положення точки на поверхні залежить від форми поверхні.
Кожна позиція визначається по відношенню хоча б до однієї іншої позиції. Координати, наприклад, визначаються відносно початку сітки системи координат. Землевпорядник вимірює «кути» кордону власності відносно раніше обстеженої контрольної точки. Геодезисти та інженери вимірюють висоти на будівельних майданчиках та в інших місцях. Висотні позначки виражаються по відношенню до вертикальної бази, еталонної поверхні, такої як середній рівень моря. Як ви, напевно, знаєте, існує також таке поняття, як горизонтальна база, хоча це складніше пояснити і візуалізувати, ніж вертикальний випадок. Горизонтальні датуми визначають геометричну залежність між сіткою системи координат і поверхнею Землі. Оскільки форма Землі складна, відносини теж є. Мета цього розділу - пояснити відносини.
Зокрема, у цьому розділі глави 2 ви навчитеся:
- Поясніть поняття горизонтальної бази
- Обчислити зміну координатного розташування через зміну з однієї горизонтальної бази на іншу
- Оцініть величину «зсуву бази», пов'язаного з коригуванням від NAD 27 до NAD 83
2.14. Геоїди
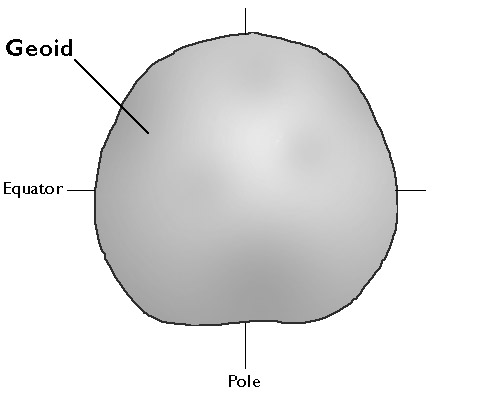
Форма Землі визначається як поверхня, яка тісно наближається до середнього глобального рівня моря, але через яку гравітація скрізь рівна. Карикатура на геоїд, показана вище, не намальована в масштабі. Нерівності сильно перебільшені
(Адаптовано від Сміта, 1988).
Точність координат, що визначають географічне розташування, залежить від того, як сітка системи координат вирівняна з поверхнею Землі. На жаль для тих, кому потрібні точні географічні дані, визначення форми поверхні Землі є нетривіальною проблемою. Настільки складна проблема, що для боротьби з нею виникла ціла професія, звана геодезією.
Геодезисти визначають поверхню Землі як поверхню, яка тісно наближається до середнього світового рівня моря, але через яку гравітація скрізь рівна. Вони називають цю форму геоїдом. Геоїди кускові, оскільки гравітація змінюється від місця до місця у відповідь на місцеві відмінності в місцевості та зміни щільності матеріалів у надрах Землі. Геоїди теж трохи присідають. Гравітація рівня моря на полюсах більша за рівень тяжіння на рівні моря на екваторі, що є наслідком «сплюснутої» форми Землі, а також відцентрової сили, пов'язаної з її обертанням.
Геодезисти Національної геодезичної зйомки США описують геоїд як «рівнопотенціальну поверхню», оскільки потенційна енергія, пов'язана з гравітаційним тягою Землі, еквівалентна скрізь на поверхні. Подібно до встановлення лінії тренду через кластер точок даних, геоїд являє собою тривимірну статистичну поверхню, яка максимально щільно підходить до вимірювань сили тяжіння, зроблених у мільйоні місць по всьому світу. У міру того, як стають доступними додаткові і більш точні гравітаційні вимірювання, геодезисти періодично переглядають геоїд. Деякі моделі геоїдів вирішуються лише для обмежених територій; GEOID03, наприклад, розраховується лише для континентальної частини США.
Нагадаємо, що горизонтальні датуми визначають, як сітки системи координат вирівнюються з поверхнею Землі. Задовго до того, як геодезисти розраховували геоїди, геодезисти використовували набагато простіші сурогати, звані еліпсоїдами, для моделювання форми Землі.
2.15. еліпсоїди
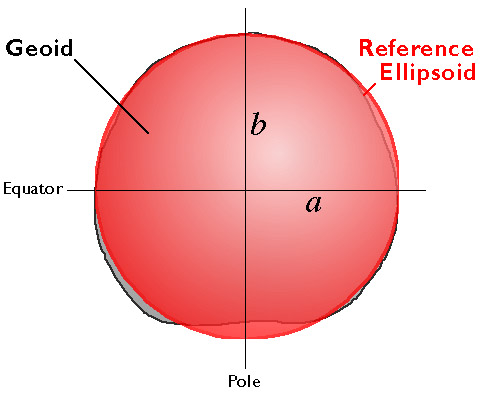
Еліпсоїди наближають геоїд (Адаптовано з Сміта, 1988).
Еліпсоїд - це тривимірна геометрична фігура, що нагадує сферу, але екваторіальна вісь якої (а - ілюстрація вище) трохи довша за її полярну вісь (b). Наприклад, екваторіальна вісь Всесвітньої геодезичної системи 1984 року приблизно на 22 кілометри довша за полярну вісь, частка, яка дуже нагадує сплюснутий сфероїд, який є планетою Земля. Еліпсоїди зазвичай використовуються як сурогати для геоїдів, щоб спростити математику, пов'язану з сіткою системи координат з моделлю форми Землі. Еліпсоїди - хороші, але не досконалі, наближення геоїдів. На карті нижче показані відмінності у висоті між моделлю геоїду під назвою GEOID96 та еліпсоїдом WGS84. Поверхня GEOID96 піднімається на 75 метрів над еліпсоїдом WGS84 над Новою Гвінею (де карта пофарбована в червоний колір). В Індійському океані (де карта забарвлена в фіолетовий колір) поверхня GEOID96 опускається приблизно на 104 метри нижче поверхні еліпсоїда.
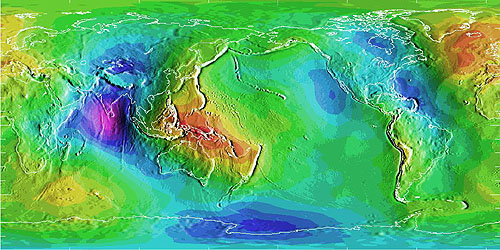
Відхилення між еліпсоїдом і геоїдом (Національна геодезична зйомка, 1997).
Багато еліпсоїди використовуються по всьому світу. (Пітер Дана опублікував список на colorado.edu) Локальні еліпсоїди мінімізують відмінності між геоїдом та еліпсоїдом для окремих країн або континентів. Наприклад, еліпсоїд Clarke 1866 мінімізує відхилення в Північній Америці. Північноамериканський Datum 1927 (NAD 27) пов'язує географічну координатну сітку з еліпсоїдом Clarke 1866. NAD 27 передбачало коригування координат широти та довготи близько 25,000 геодезичних контрольних пунктів по всій території США Загальнонаціональне коригування почалося з початкового контрольного пункту на ранчо Мідс, штат Канзас, і мав на меті примирити розбіжності між багатьма місцевими та регіональними контролями обстежень, які передували йому.
Північноамериканський Datum 1983 (NAD 83) передбачав ще одну загальнонаціональну коригування, яка частково вимагала прийняття нового еліпсоїда, який називається GRS 80. На відміну від Clarke 1866, GRS 80 - це глобальний еліпсоїд, зосереджений на центрі мас Землі. GRS 80 по суті еквівалентна WGS 84, глобальному еліпсоїду, на якому базується Глобальна система позиціонування. NAD 27 і NAD 83 вирівнюють сітки системи координат з еліпсоїдами. Відрізняються вони просто тим, що відносяться до різних еліпсоїдів. Оскільки Clarke 1866 і GRS 80 дещо відрізняються за формою, а також положеннями своїх центральних точок, регулювання від NAD 27 до NAD 83 передбачало зсув географічної координатної сітки. Оскільки різноманітні датуми залишаються у використанні, геопросторові професіонали повинні розуміти цей зсув, а також те, як трансформувати дані між горизонтальними датумами.
2.16. Контрольні точки та зрушення бази

У США горизонтальні пункти контролю високого порядку позначені постійними металевими «пам'ятниками», як показано вище. Фізичним проявом бази є мережа вимірювань контрольних точок (Національна геодезична зйомка, 2004).
Геоїди, еліпсоїди і навіть системи координат - все це абстракції. Той факт, що «горизонтальна база» відноситься до зв'язку між еліпсоїдом і системою координат, двома абстракціями, може пояснити, чому поняття так часто неправильно розуміється. Однак датуми мають фізичні прояви.
Наведена вище одна з приблизно двох мільйонів горизонтальних і вертикальних контрольних точок, які були встановлені в США Хоча маркери контрольних точок фіксовані, координати, які визначають їх розташування, можуть змінюватися. Національна геодезична зйомка США веде базу даних специфікацій координат цих контрольних пунктів, включаючи історичні місця, а також останні коригування. Однією з причин для коригування координат контрольної точки є прийняття нових горизонтальних датумів. Оскільки кожна сітка системи координат вирівнюється з еліпсоїдом, який наближає форму Землі, координатні сітки обов'язково зсуваються, коли один еліпсоїд замінюється іншим. Коли сітки системи координат зсуваються, координати, пов'язані з фіксованими контрольними точками, повинні бути скориговані. Те, як ми враховуємо форму Землі, має значення у тому, як ми вказуємо місця.
СПРОБУЙ ЦЕ!
Ось шанс обчислити, наскільки змінюються координати контрольної точки у відповідь на коригування від північноамериканської Datum 1927 (на основі еліпсоїда Clarke 1866) до північноамериканської Datum 1983 (на основі еліпсоїда GRS 80). Вам буде запропоновано інтерпретувати ваші результати в майбутній практичній вікторині.
-
Знайти географічні координати населеного пункту
- Почніть з інформаційної системи географічних назв USGS при Раді США з географічних назв
- Перейдіть за посиланнями з позначкою «Внутрішні назви», а потім Пошук для пошуку топонімів, включених в Інформаційну систему географічних назв.
- У формі запиту введіть назву вашого рідного міста (або іншого названого географічного об'єкта) у полі Назва об'єкта, а також ваш домашній стан. Виберіть «Населене місце» (або інше, якщо доречно) для класу об'єктів.
- Якщо ваш будинок знаходиться в іншому місці, ніж США, введіть назву цікавого місця або місце призначення фантазії (наприклад, «Лас-Вегас»; -).
- Натисніть Надіслати запит.
- Результат повинен включати координати широти та довготи центроїда, який відображає, де назва вашого міста (або іншої функції) буде відображатися на карті. Ці координати вам знадобляться для наступного кроку.
-
Знайти географічні координати сусідньої горизонтальної контрольної точки
- Відвідайте домашню сторінку Національної геодезичної зйомки США
- Перейдіть за посиланням з написом Опитування Марка D atasheets
- На сторінці NGS Datasheet перейдіть за посиланням з написом Таблиці даних.
- Ви можете почати з «Info Link» з написом «Розкажіть мені більше про таблиці даних»
- На сторінці пошуку таблиць даних NGS перейдіть за посиланням з написом «Радіальний пошук». (Ви можете експериментувати з іншим методом пошуку, якщо хочете.)
- На NGS Datasheet Радіус точки форми:
- Введіть координати широти та довготи, які ви переглянули на кроці #1. Зверніть увагу на формат введення.
- Вкажіть радіус пошуку.
- Виберіть Будь-який Horz і/або Vert. Керування з поля прокрутки Тип даних Бажаний.
- Виберіть «Будь-яка стабільність» з поля прокрутки бажаної стабільності.
- Натисніть Надіслати.
- Результатом має бути форма результатів списку станцій, яка виглядає як вміст вікна, зображеного нижче. Це результати мого пошуку координат центроїда для Державного коледжу ПА. Зверніть увагу, що я виділив станцію, яка є найближчою до координат, які я ввів, і контрольну точку першого порядку (див. «1″ під стовпцем з написом «H»?)
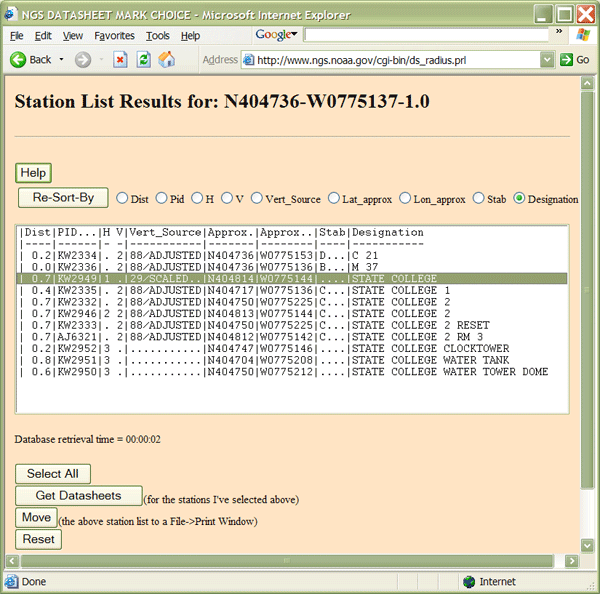
- Виберіть станцію, найближчу до вказаних вами координат, яка також є горизонтальною контрольною точкою найвищого порядку.
- Натисніть Отримати таблиці даних. Система повинна відповідати таблицею даних станції, як у цьому прикладі.
- У прикладі, пов'язаному вище, ПОТОЧНИЙ КОНТРОЛЬ ОБСТЕЖЕННЯ точки станції вказано як NAD 83 (1992) 40 48 13.83840 (N) 077 51 44.25410 (W) СКОРИГОВАНИЙ. Це географічні координати контрольної точки щодо горизонтальної бази NAD 83. На наступному кроці ми побачимо, наскільки контрольна точка «перемістилася» в результаті коригування цих координат з попередньої бази NAD 27. (Географічні координати контрольної точки задаються до 100,000-ї секундної точності, або приблизно 0,3 мм довготи. Однак майте на увазі різницю між точністю та точністю; кінцевий 0 говорить про те, що точність на порядок менше, ніж точність.)
-
Обчислення зсуву бази, пов'язаного з перетворенням з однієї горизонтальної бази на іншу
- Повернутися на домашню сторінку Національної геодезичної зйомки США
- Перейдіть за посиланням з міткою набір геодезичних інструментів.
- На сторінці набору геодезичних інструментів NGS перейдіть за посиланням NADCON (ви перейдете на пояснювальну сторінку, де вам потрібно буде знову натиснути NADCON, щоб перейти до утиліти).
- На сторінці Утиліта перетворення даних в Північній Америці прочитайте вступні абзаци, а потім перейдіть за посиланням з написом Інтерактивно обчислити зсув даних між NAD 27 та NAD 83. Посилання, про яке йдеться в попередньому реченні, нещодавно було видалено. Замість цього натисніть на посилання тут в***Повідомлення... у верхній частині сторінки.
- У формі обчислень NADCON під заголовком обчислити зсув бази для певного місця:
- Оберіть напрямок перетворення: NAD 83 до NAD27
- Введіть координати широти та довготи NAD 83 вашої станції керування. Зверніть увагу на формат.
- Клацніть «Обчислити зсув бази для одного місця».
- Результатом має бути звіт про вихід NADCON, як у цьому прикладі. У прикладі Державного коледжу коригування від NAD 83 до NAD 27 (пов'язане із заміною старого еліпсоїда Clarke 1866 на еліпсоїд, орієнтований на Землю GRS 80, призвело до зміщення сітки географічної системи координат майже 7 метрів на південь і більше 23 метрів на захід. Цей зсув сітки відображається у коригуванні координат, які визначають розташування контрольної точки. Зверніть увагу, що точка не рухалася, скоріше, сітка змістилася. Скільки зрушення відбулося на вашому місці?
ПРАКТИКА ВІКТОРИНИ
Зареєстровані студенти штату Пенн повинні повернутися зараз до папки Chapter 2 в ANGEL (через меню Ресурси ліворуч), щоб пройти самооцінку вікторини про горизонтальні дані.
Ви можете приймати практичні вікторини стільки разів, скільки хочете. Вони не забиваються і ніяк не впливають на вашу оцінку.
2.17. Перетворення координат
Фахівцям ГІС часто потрібно перетворити дані з однієї системи координат та/або бази в іншу. Наприклад, цифрові дані, отримані картами кальки над оцифрующим планшетом, повинні бути перетворені з негеографічної системи координат площини планшета в площину з географічною прив'язкою або сферичну систему координат, яка може бути геозареєстрована з іншими цифровими даними «шарами». Сирі дані зображення, отримані скануванням поверхні Землі з космосу, як правило, перекошені геометрично в результаті супутникових орбіт та інших факторів; щоб бути корисними, вони також повинні бути перетворені в географічні системи координат. Навіть точкові дані, отримані GPS-приймачами, які вимірюються як координати широти та довготи на основі бази WGS84, часто потребують перетворення в інші системи координат або датуми, щоб відповідати специфікаціям проекту. У цьому розділі описано три категорії перетворень координат: (1) перетворення координат площини; (2) перетворення базових даних; і (3) проекції карти.
Студенти, які успішно завершили цей розділ глави 2, повинні мати можливість:
- Визнайте тип перетворення, який підходить для геореєстрації двох або більше наборів даних.
2.18. Трансформації координат площини
Деякі перетворення координат прості. Наприклад, перетворення з координат площини, що не прив'язані до географічних координат полярних координат, показаних нижче, передбачає не що інше, як заміну одного виду координат іншим.
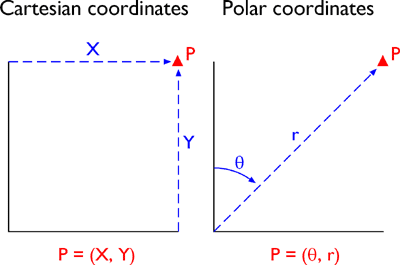
Те саме положення вказано у двох негеографічних системах координат площини: декартової (ліворуч) та полярної (праворуч) (адаптовано з Iliffe, 2000).
На жаль, більшість проблем перетворення координат площини не такі прості. Геометрії негеографічних систем координат площини та географічних систем координат площини, як правило, дуже різні, головним чином тому, що часто проектуються системи координат площини з географічними прив'язками. Як відомо, акт проекції майже сферичної поверхні на двомірну площину обов'язково спотворює геометрію вихідної сферичної поверхні. Зокрема, масштаб проектованої карти (або невиправленої аерофотознімки, якщо на те пішло) змінюється від місця до місця. До тих пір, поки географічна область інтересу не надто велика, однак, формули, як описані тут, можуть бути ефективними при перетворенні сітки системи координат не прив'язки площини, щоб відповідати сітці системи координат площини з географічною прив'язкою з розумною та вимірною точністю. Ми не будемо вдаватися в математику перетворень тут, оскільки формули реалізовані в програмному забезпеченні ГІС. Натомість цей розділ має на меті ознайомити вас з тим, як працюють деякі загальні перетворення та як вони можуть бути використані.
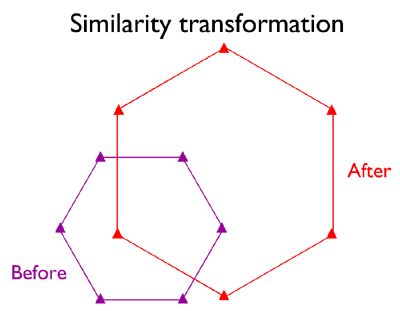
ПЕРЕТВОРЕННЯ ПОДІБНОСТІ
На гіпотетичній ілюстрації нижче показано просторове розташування шести контрольних точок, оцифрованих з паперової карти («до»), відрізняється від просторового розташування тих же точок, які з'являються на географічній аерофотознімці, яка посилається на іншу сітку системи координат площини («після»). Якщо, як показано, розташування двох наборів точок відрізняється лише масштабом, обертанням та зміщенням, відносно просте перетворення подібності з чотирма параметрами може зробити трюк. Ваше програмне забезпечення ГІС має виводити параметри для вас, порівнюючи відносні положення загальних точок. Зауважте, що хоча ілюстровані лише шість контрольних точок, рекомендується від десяти до двадцяти контрольних точок (Chrisman 2002).
Шість місць розташування контрольних точок до і після перетворення подібності використовуються для виправлення систематичних відмінностей у масштабі, обертанні та зміщенні між двома системами координат площини.
СПРОБУЙ ЦЕ!
Клацніть на графіку вище, щоб переглянути Flash-анімацію (transform_sim.swf) в окремому вікні браузера.
Примітка. Для завершення цієї дії вам потрібно буде встановити програвач Adobe Flash. Якщо ви ще не встановили Flash player, ви можете завантажити його безкоштовно з Adobe.
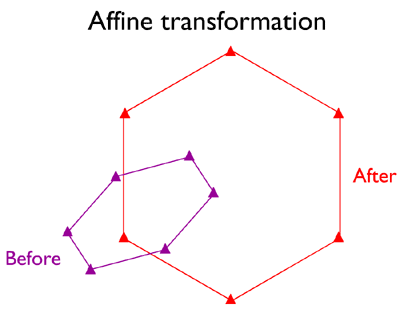
АФФІННЕ ПЕРЕТВОРЕННЯ
Іноді трансформація подібності не робить хитрості. Наприклад, оскільки паперові карти розширюються і стискаються більше вздовж зерна паперу, ніж поперек зерна у відповідь на зміни вологості, масштаб паперової карти, ймовірно, буде трохи більшим вздовж однієї осі, ніж інша. У таких випадках шестипараметричне афінне перетворення може бути використано для розміщення різниць у масштабі, обертанні та зміщенні уздовж кожного з двох вимірів систем координат джерела та цілі. Ця характеристика особливо корисна для перетворення даних зображення, відсканованих з полярно-орбітальних супутників, орбіти яких простежують S-подібні шляхи над обертовою Землею.
Шість місць розташування контрольних точок до і після аффінного перетворення використовуються для виправлення систематичних відмінностей у масштабі, обертанні та зміщенні між двома системами координат площини. Зверніть увагу, що розташування точок перед перетворенням є перекосованим, а також зміщенням та поверненням.
СПРОБУЙ ЦЕ!
Клацніть на графіку вище, щоб переглянути Flash-анімацію (transform_aff.swf) в окремому вікні браузера.
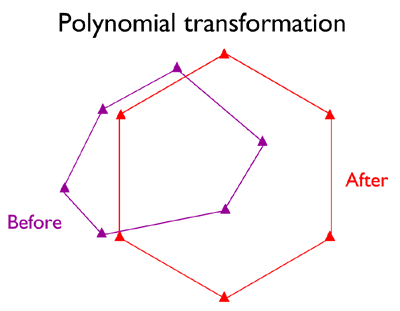
ПЕРЕТВОРЕННЯ ПОЛІНОМА ДРУГОГО ПОРЯДКУ
Коли ні подібність, ні афінні перетворення не дають прийнятних результатів, можливо, доведеться вдатися до дванадцятипараметричного поліноміального перетворення другого порядку. Їх перевага полягає в можливості корекції наборів даних, які спотворюються відразу декількома способами. Недоліком є те, що стабільність результатів дуже залежить від кількості та розташування контрольних точок та ступеня несхожості геометрії джерела та цілі (Iliffe 2000).
Шість місць розташування контрольних точок до і після многочленного перетворення другого порядку. Зверніть увагу, що розташування точок перед перетворенням спотворюється різними способами в порівнянні з виправленим розташуванням.
СПРОБУЙ ЦЕ!
Клацніть на графіку вище, щоб переглянути Flash-анімацію (transform_poly.swf) в окремому вікні браузера.
Ще більш складні методи перетворення площини, відомі разом як гумове покриття, оптимізують прилягання набору вихідних даних до геометрії цільового набору даних так, ніби вихідні дані були відображені на розтягується аркуші.
КОРІНЬ СЕРЕДНЯ КВАДРАТНА ПОМИЛКА
Програмне забезпечення ГІС забезпечує статистичний показник того, наскільки добре набір перетворених контрольних точок відповідає положенням тих же точок у цільовому наборі даних. Простіше кажучи, помилка середнього квадрата кореня (RMS) - це середнє значення відстаней (також відомих як залишки) між кожною парою контрольних точок. Що являє собою прийнятно низьку RMS Error залежить від характеру проекту та масштабу аналізу.
2.19. Трансформації бази даних
Місця розташування точок задаються через (а) їх положення відносно деякої сітки системи координат і (b) їх висоти над або нижче якоїсь опорної поверхні. Очевидно, що висота нерухомої точки залежить від розміру та форми опорної поверхні (наприклад, середнього рівня моря), на якій базується вимірювання висоти. Таким же чином положення точки в сітці системи координат залежить від розміру та форми поверхні, на яку драпірується сітка. Зв'язок між сіткою і моделлю поверхні Землі називається горизонтальною базою. Фахівці ГІС, які покликані об'єднувати набори даних, вироблені в різний час і в різних куточках світу, повинні бути обізнаними про перетворення даних.
NAD 27 до NAD 38
У США двома найбільш часто зустрічаються горизонтальними датумами є північноамериканський Datum 1927 (NAD 27) та північноамериканський Datum 1983 (NAD 83). Поява Глобальної системи позиціонування зумовило необхідність оновлення NAD 27, що включало (а) прийняття геоцентричного еліпсоїда GRS 80 замість еліпсоїда Clarke 1866; і (b) виправлення багатьох спотворень, які накопичилися в старій датумі. Маючи на увазі, що реалізація бази - це мережа фіксованих місць розташування контрольних точок, які були вказані відносно тієї ж опорної поверхні, коригування північноамериканської бази 1983 року спричинило значення координат кожної контрольної точки, керованої Національною геодезичною зйомкою ( NGS) змінити. Очевидно, що самі точки не зміщувалися через перетворення бази (хоча вони рухалися на сантиметр або більше на рік через тектоніку плит). Швидше за все, т сітки системи координат на основі бази зміщені по відношенню до нового еліпсоїда. А оскільки локальні спотворення були скориговані одночасно, величина зсуву сітки змінюється від місця до місця. Наведені нижче ілюстрації порівнюють величину зсувів сітки, пов'язаних з коригуванням NAD 83 в одному місці та по всій країні.
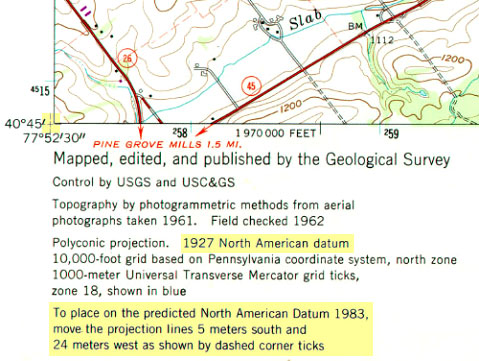
Кут топографічної карти чотирикутника масштабу 1:24 000 для Державного коледжу ПА, що показує величину зсуву сітки, пов'язаного з коригуванням NAD 83. Карта заснована на NAD 27, але була передрукована з ревізіями в 1987 році, включаючи твердження про те, що лінії сітки системи координат зсуваються 24 метри на захід і 5 метрів на південь, якщо замість NAD 27 використовуються координати NAD 83.
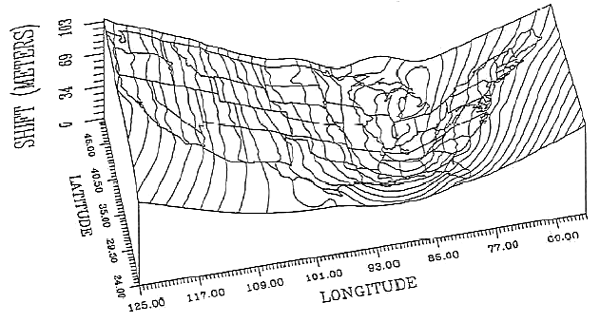
Величина зсуву сітки пов'язана з коригуванням NAD 83 для континентальних 48 штатів США. Зсуви варіюються від 10 до 100 метрів у нижніх 48 (найменше у верхніх штатах Середнього Заходу) до понад 200 метрів на Алясці та понад 400 метрів на Гаваях (Dewhurst 1990).
Враховуючи нерівномірність зсуву, NGS не могла запропонувати простий алгоритм перетворення, який геодезисти та картографи могли б використовувати для коригування локальних даних на основі старих даних. Натомість NGS створив програмну програму під назвою NADCON (Dewhurst 1990, Mulcare 2004), яка обчислює скориговані координати з визначених користувачем вхідних координат шляхом інтерполяції з пари 15° корекційних сіток, створених NGS з сотень тисяч раніше скоригованих контрольних точок.
СПРОБУЙ ЦЕ!
Спробуйте інструмент NADCON Національної геодезичної зйомки.
GPS ДАНІ ТА WGS 84
Міністерство оборони США створило Глобальну систему позиціонування (GPS) протягом 16 років при стартовій вартості близько 10 мільярдів доларів. GPS-приймачі обчислюють свої позиції з точки зору широти, довготи та висоти над або нижче Всесвітньої геодезичної системи 1984 еліпсоїда (WGS 84). Розроблений спеціально для Глобальної системи позицій, WGS 84 - це еліпсоїд, орієнтований на Землю, який, на відміну від багатьох регіональних, національних та локальних еліпсоїдів, які все ще використовуються, мінімізує відхилення від геоїда у всьому світі. Залежно від того, де може працювати фахівець з ГІС, або з якими даними йому може знадобитися працювати, ймовірно, виникне необхідність перетворення даних GPS з WGS 84 на якусь іншу базу даних. Алгоритми перетворення даних реалізуються в програмному забезпеченні ГІС, а також у програмному забезпеченні для подальшої обробки, що надається постачальниками GPS для використання з їх приймачами. Деякі алгоритми перетворення дають більш точні результати, ніж інші. Метод, який ви виберете, буде залежати від того, який вибір доступний вам і наскільки точності вимагає ваша програма.
На відміну від плоских перетворень, описаних раніше, базові перетворення включають еліпсоїди і тому є тривимірними. Найпростішим є трьохпараметричне перетворення Молоденського. На додаток до знань про розмір і форму еліпсоїдів джерела та мішені (задається через велику піввісь, відстань від екватора еліпсоїда до його центру та коефіцієнт сплющення, ступінь, до якої еліпсоїд сплющений, щоб наблизити сплюснуту форму Землі) , зміщення між двома еліпсоїдами має бути вказано вздовж осей X, Y та Z. Вікно, показане нижче, ілюструє еліпсоїдальні та зсувні параметри для декількох горизонтальних датумів, всі виражені стосовно WGS 84.
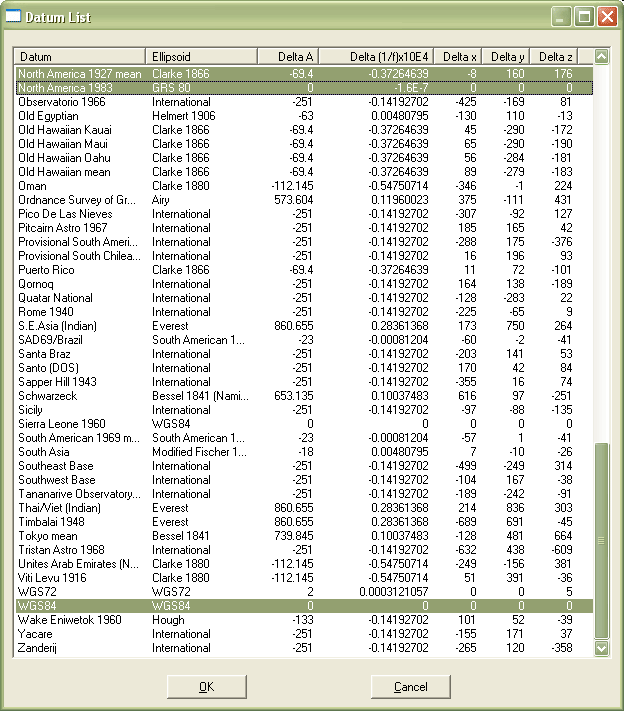
Вікно списку даних в програмній утиліті Waypoint+ (Hildebrand 1997). NAD 27, NAD 83 і WGS 84 виділені. Еліпсоїд, пов'язаний з кожною базою, називається, а його розмір і форма вказані (Delta A і Delta (1/f) x10e4), а також три параметри зсуву, в метрах, відносно WGS 84 (Delta x, Delta y, Delta z).
Для більших областей дослідження більш точні результати можуть бути отримані за допомогою семипараметричного перетворення, що враховує обертання, а також масштабування та зсув.
Нарешті, поверхневі перетворення, такі як описана вище інтерполяція сітки NADCON, дають найкращі результати на найбільших ділянках.
Для рутинних картографічних програм, що охоплюють відносно невеликі географічні райони (тобто більше 1:25 000), описані раніше площинні перетворення можуть дати адекватні результати, коли технічні характеристики даних невідомі і коли можна ідентифікувати достатню кількість належним чином розподілених контрольних точок.
2.20. Картографічні прогнози
Координати широти та довготи визначають позиції в більш-менш сферичній сітці, яка називається гратикулою. Координати площини, такі як схід і північ у системах Універсального поперечного Меркатора (UTM) та координати площини стану (SPC), позначають положення в сплющених сітках. Ось чому географічні координати площини називаються проектованими, а географічні координати називаються непроектованими. Математичні рівняння, що використовуються для перетворення координат широти та довготи в координати площини, називаються картографічними проекціями. Формули зворотної проекції перетворюють координати площини в географічні. Найпростіший вид проекції, проілюстрований нижче, перетворює решітку в прямокутну сітку, в якій всі лінії сітки прямі, перетинаються під прямим кутом і однаково розташовані. Більш складні проекції дають сітки, в яких довжини, форми та відстань між лініями сітки змінюються.
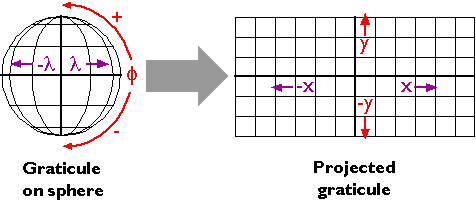
Проекції карти - це математичні перетворення між географічними координатами та координатами площини.
Якщо ви практикуєте ГІС, ви, ймовірно, зіткнулися з необхідністю накладення непроектованих даних про широту та довготу на прогнозовані дані, і навпаки. Наприклад, вам може знадобитися об'єднати географічні координати, виміряні за допомогою GPS-приймача, з цифровими даними, опублікованими USGS, які кодуються як координати UTM. Сучасне програмне забезпечення ГІС надає складні інструменти для проектування та непроектування даних. Щоб використовувати такі інструменти найбільш ефективно, вам потрібно зрозуміти проекційні характеристики наборів даних, які ви збираєтеся об'єднати. Ми детально розглянемо проекції карт в інших місцях цього уроку. Тут давайте просто переглянемо характеристики, які включені в розділ «Інформація про просторові посилання» документів метаданих, які (в ідеалі!) супроводжувати набори даних, які ви, можливо, захочете включити у свою ГІС. До них відносяться:
- Назва проекції Найпоширенішим у сфері ГІС є Поперечний Меркатор, який служить основою глобальної системи координат площини UTM, Великобританії та запропонованих національних мереж США та багатьох зон у системі координат штату США (SPC). Інші зони SPC засновані на конічній конформній проекції Ламберта, яка, як і багато проекцій, названа на честь свого винахідника, а також категорії проекції (конічної) та геометричних властивостей, які вона зберігає (конформні). Багато картографічних даних, особливо у вигляді друкованих паперових карт, базуються на «застарілих» проекціях (таких як Поліконічний у США), які більше не використовуються широко. Значно більша різноманітність типів проекцій, як правило, використовується в дрібномасштабному тематичному картографуванні, ніж у великомасштабному еталонному відображенні.
- Центральний меридіан Хоча сухопутні маси не показані, припустимо, що гратикула та проектована сітка, показані вище, зосереджені на перетині екватора (0 широта) та простого меридіана (довгота 0°). Більшість формул проекції карти містять параметр, який дозволяє центрувати проектовану карту на будь-якій довготі.
- Широта початку проекції За певних умов більшість формул проекції карти дозволяють вказати різні аспекти сітки. Замість екваторіального аспекту, показаного вище, ви можете вказати полярний аспект або похилий аспект, змінюючи широту початку проекції таким чином, щоб один із полюсів або будь-яка широта між полюсом та екватором була зосереджена на проектованій карті. Як ви могли собі уявити, зовнішній вигляд сітки сильно змінюється при розгляді в різних аспектах.
- Масштабний коефіцієнт на Центральному меридіані Це співвідношення масштабу карти по центральному меридіану і масштабу на стандартному меридіані, де спотворення масштабу дорівнює нулю. Масштабний коефіцієнт на центральному меридіані становить 0,9996 в кожній із зон системи координат 60 UTM, оскільки кожна містить дві стандартні лінії на 180 кілометрів на захід та схід від центрального меридіана. Викривлення масштабу збільшується з відстанню від стандартних ліній у всіх системах координат проекції.
- Стандартні лінії Деякі проекції, включаючи конічну конформну Ламберта, включають параметри, за допомогою яких можна задати одну або дві стандартні лінії, уздовж яких немає спотворення масштабу, викликаного актом перетворення сферичної сітки в плоску сітку. З тих самих міркувань, що дві стандартні лінії розміщуються в кожній зоні UTM, щоб мінімізувати спотворення по всій зоні максимум до однієї частини в 1000, дві стандартні паралелі розміщуються в кожній зоні SPC, яка заснована на проекції Ламберта, таким чином, що спотворення масштабу не гірше однієї частини в 10,000 де завгодно в зоні.
ПРАКТИКА ВІКТОРИНИ
Зареєстровані студенти штату Пенн повинні повернутися зараз до папки Chapter 2 в ANGEL (через меню Ресурси ліворуч), щоб пройти тест самооцінки про перетворення координат.
Ви можете приймати практичні вікторини стільки разів, скільки хочете. Вони не забиваються і ніяк не впливають на вашу оцінку.
2.21. Система координат UTM
Нижче показаний південно-західний кут топографічної карти масштабу 1:24 000, опублікованої Геологічною службою США (USGS). Зверніть увагу, що географічні координати (40 45′ N широти, 77° 52′ 30″ W довготи) кута вказані. Також показані, однак, галочки та мітки, що представляють дві плоскі системи координат, систему універсального поперечного Меркатора (UTM) та систему координат стану площини (SPC). Галочка з написом «4515» являє собою лінію сітки UTM (називається «північ»), яка проходить паралельно екватору і 4515 000 метрів на північ від нього. Кліщі з позначкою «258» та «259» представляють лінії сітки, які проходять перпендикулярно екватору та 258 000 метрів та 259 000 метрів на схід відповідно походження сітки UTM Zone 18 North. На відміну від ліній довготи, UTM «східні» прямі і не сходяться на полюсах Землі. Все це напрошується питання: Чому на карті показано декілька сіток системи координат? Чому географічних координат недостатньо?

Південно-західний кут топографічної карти USGS із зображенням сітки та міток для трьох різних систем координат, включаючи систему координат UTM. (USGS. «Чотирикутник Державного коледжу, Пенсільванія»)
Ви можете думати про плоску систему координат як зіставлення двох шкал вимірювання. Іншими словами, якби ви розмістили дві лінійки під прямим кутом, таким чином, щоб позначки «0» лінійки вирівняли, ви б визначили систему координат площини. Лінійки називаються «сокирами». Абсолютне розташування будь-якої точки простору в системі координат площини визначається через виміри відстані по осях x (схід-захід) і y (північ-південь). Позиція, визначена координатами (1,1), розташована на одну одиницю праворуч, а на одну одиницю вгору від початку (0,0). Сітка UTM - це широко використовуваний тип геопросторової системи координат площини, в якій позиції задаються як східні (відстані, у метрах, на схід від початку) та північ (відстані на північ від початку).
На відміну від цього, сітка географічної системи координат широт і довгот складається з двох криволінійних шкал вимірювання, щоб відповідати майже сферичній формі Землі. Як відомо, географічні координати задаються в градусах, хвилинах і секундах дуги. Вигнуті сітки незручно використовувати для побудови позицій на плоских картах. Крім того, обчислення відстаней, напрямків та областей зі сферичними координатами є громіздким порівняно з координатами площини. З цих причин картографи та військові чиновники Європи та США розробили систему координат UTM. Тепер сітки UTM є стандартними не тільки на друкованих топографічних картах, але і для геопросторової прив'язки цифрових даних, які складають нову «Національну карту США».
У цьому розділі глави 2 ви навчитеся:
- Опишіть характеристики системи координат UTM, включаючи її основу у проекції поперечної карти Меркатора; і
- Ділянка координат UTM на карті
2.22. Сітка UTM та поперечна проекція Меркатора
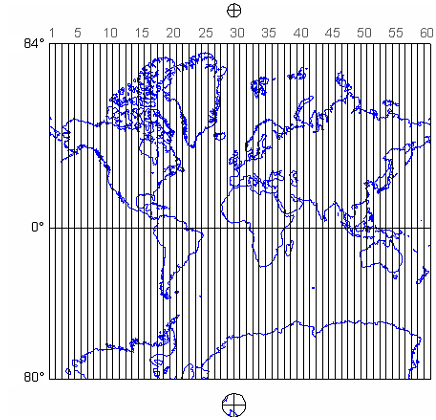
Проекція Меркатора світу, що показує зони системи координат 60 UTM, кожна з яких розділена на північну та південну половини на екваторі. Також показані дві полярні системи координат, які використовуються для визначення позицій за північними та південними межами системи UTM.
Універсальна поперечна система Меркатора насправді не є універсальною, але вона охоплює майже всю поверхню Землі. Виключені лише полярні райони - широти вище 84° північ і 80° на південь. (Полярні системи координат використовуються для визначення позицій за межами цих широт.) Система UTM ділить решту поверхні Землі на зони 60, кожна з яких охоплює 6° довготи. Вони пронумеровані з заходу на схід від 1 до 60, починаючи з 180° західної довготи (приблизно збігається з Міжнародною лінією дат).
На ілюстрації вище зображені зони UTM так, ніби вони рівномірно «широкі» від екватора до північних і південних меж. Насправді, оскільки меридіани сходяться до полюсів на земній кулі, кожна зона UTM звужується від 666,000 метрів «шириною» на екваторі (де 1° довготи становить близько 111 кілометрів у довжину) до лише близько 70 000 метрів на 84° північ і близько 116000 метрів на 80° на південь.
«Поперечний Меркатор» відноситься до способу перетворення географічних координат в координати площини. Такі перетворення називаються картографічними проекціями. На малюнку нижче показані зони 60 UTM, як вони з'являються при проектуванні за допомогою поперечної формули проекції карти Меркатора, оптимізованої для зони UTM, виділеної жовтим кольором, зона 30, яка охоплює 6° на захід до 0° східної довготи (основний меридіан).
Як ви можете собі уявити, ви не можете згладити глобус, не зламавши або розірвавши його якось. Аналогічно, акт математичного перетворення географічних координат в координати площини обов'язково витісняє більшість (але не всі) перетворених координат в деякій мірі. Через це масштаб карти змінюється в межах проектованих (плоских) сіток системи координат UTM.
Еліпси спотворень, нанесені червоним кольором, допомагають нам візуалізувати картину спотворення масштабу, пов'язаного з певною проекцією. Якби не сталося спотворень у процесі проектування карти, показаної нижче, всі еліпси були б однакового розміру та круглої форми. Як бачите, еліпси, розташовані в центрі виділеної зони UTM, мають однаковий розмір і форму. Далеко від виділеної зони еліпси неухильно збільшуються в розмірах, хоча їх форми залишаються рівномірно круглими. Цей шаблон вказує на те, що спотворення масштабу є мінімальним у зоні 30, а масштаб карти збільшується від цієї зони. Крім того, еліпси показують, що характер спотворень, пов'язаний з цією проекцією, полягає в тому, що форми об'єктів, як вони з'являються на земній кулі, зберігаються, а їх відносні розміри спотворюються. Картографічні проекції, які зберігають форму, жертвуючи вірністю розмірів, називаються конформними проекціями. Плоскі системи координат, які найбільш широко використовуються в США, UTM та SPC (система координат штату площині) засновані на конформних проекціях.
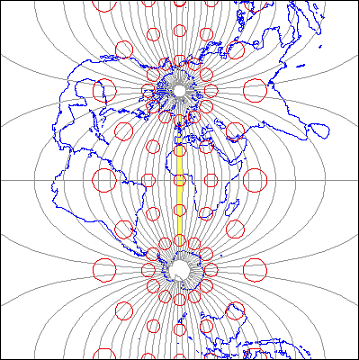
Результат поперечної проекції Меркатора світу з центром на UTM Zone 30. Червоні кола виявляють спотворення масштабу, введене при перетворенні від географічних до проектованих плоских координат. На земній кулі всі кола були б однакового розміру.
Поперечна проекція Меркатора, проілюстрована вище, мінімізує спотворення в зоні UTM 30. П'ятдесят дев'ять варіацій цієї проекції використовуються для мінімізації спотворень в інших 59 зонах UTM. У кожному випадку спотворення становить не більше 1 частини на 1000. Це означає, що відстань 1,000 метрів, виміряна в будь-якому місці зони UTM, буде не гіршою, ніж + або - 1 метр.
Анімація, пов'язана з ілюстрацією нижче, показує серію з 60 поперечних проекцій Меркатора, які утворюють 60 зон системи UTM. Кожна зона базується на унікальній проекції поперечної карти Меркатора, яка мінімізує спотворення в межах цієї зони. Зони нумеруються від 1 до 60 на схід від міжнародної лінії дат. Анімація починається з зони 1.
Один кадр анімації, що показує послідовність 60 поперечних проекцій Меркатора, що використовуються в якості основи системи координат UTM. Червоним кольором виділено UTM Zone 01, яка охоплює 180° W до 174° W. Унікальна проекція використовується для кожної зони UTM, завдяки чому деформація в кожній зоні зводиться до мінімуму.
СПРОБУЙ ЦЕ!
Клацніть на графіку вище, щоб переглянути файл анімації (utm.avi, 0.5 Mb) в окремому вікні Microsoft Media Player.
Щоб переглянути ту ж анімацію у форматі QuickTime (utm.mov, 2.9 Мб), натисніть тут. Потрібен плагін QuickTime, який доступний безкоштовно на apple.com.
Проекції карти - це математичні формули, що використовуються для перетворення географічних координат в координати площини. (Формули зворотної проекції перетворюють координати площини назад у широти та довготи.) «Поперечний Меркатор» - одна з гіпотетично нескінченного числа таких проекційних формул. Нижче з'являється візуальний аналог поперечної проекції Меркатора. Концептуально поперечна проекція Меркатора переносить позиції на земній кулі у відповідні положення на циліндричній поверхні, яка згодом розрізається від кінця до кінця і сплющується. На ілюстрації циліндр дотичний до земної кулі уздовж однієї лінії, званої стандартною лінією. Як показано на карті маленького світу поруч із земною кулею та циліндром, спотворення масштабу є мінімальним вздовж стандартної лінії і збільшується з відстанню від неї. Анімація, пов'язана вище, була вироблена шляхом обертання циліндра 59 разів з кроком 6°.
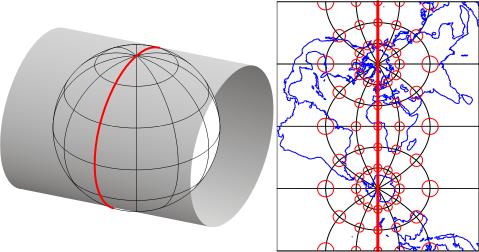
Наведена вище карта являє собою поперечну проекцію Меркатора світу зі стандартним меридіаном на 0° довготи. (Зауважте, що через дуже малий розмір карти гратикула відображається з роздільною здатністю 30°.) Глобус, загорнутий у циліндр, є концептуальною моделлю того, як формула поперечної проекції Меркатора передає позиції на земній кулі до позицій на площині (Циліндр може бути сплющений до поверхні площини після того, як він розгорнутий з земної кулі.) Більш товста червона лінія на циліндрі і карті є стандартною лінією, по якій спотворення масштабу дорівнює нулю. Як вказують еліпси спотворень на карті, спотворення збільшується з відстанню від стандартної лінії.
На ілюстрації вище є один стандартний меридіан. Деякі формули проекції, включаючи поперечну проекцію Меркатора, допускають дві стандартні лінії. Кожна з 60 варіацій поперечної проекції Меркатора, яка використовується як фундамент зон 60 UTM, використовує не одну, а дві стандартні лінії. Ці дві стандартні лінії паралельні і 180 000 метрів на схід і захід від кожного центрального меридіана. Ця схема гарантує, що максимальна похибка, пов'язана з проекцією через спотворення шкали, складе 1 частина на 1000 (у зовнішнього краю зони на екваторі). Похибка, обумовлена спотворенням шкали на центральному меридіані, становить 1 частина на 2500. Спотворення дорівнює нулю, звичайно, по стандартних лініях.
Так що ж означає термін «поперечний»? Це просто стосується того, що циліндр, показаний вище, був повернутий на 90° від екваторіального аспекту стандартної проекції Меркатора, в якій одна стандартна лінія збігається з широтою 0°.
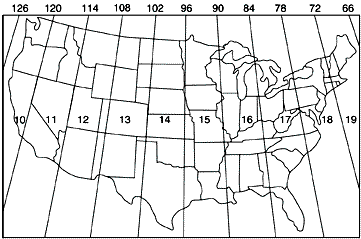
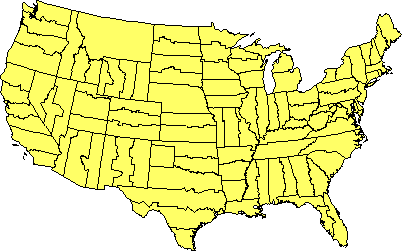
Десять зон UTM, які охоплюють межі США (Геологічна служба США, 2004).
Одним з недоліків системи UTM є те, що для обліку великих об'єктів необхідно використовувати кілька систем координат. Наприклад, нижні 48 Сполучених Штатів поширюються на десять зон UTM. Той факт, що існує багато вузьких UTM зон, може призвести до плутанини. Наприклад, місто Філадельфія, штат Пенсільванія, знаходиться на схід від міста Піттсбург. Якщо порівняти східні центри центроїдів, що представляють два міста, однак, Східна Філадельфія (близько 486 000 метрів) менше, ніж Пітсбург (близько 586 000 метрів). Чому? Тому що, хоча міста обидва розташовані в штаті Пенсільванія США, вони розташовані в двох різних зонах UTM. Як це трапляється, Філадельфія ближче до походження своєї Зони 18, ніж Піттсбург до походження своєї Зони 17. Якби ви намалювали точки, що представляють два міста, на карті, ігноруючи той факт, що дві зони є двома різними системами координат, Філадельфія з'явиться на захід від Піттсбурга. Недосвідчені користувачі ГІС роблять цю помилку весь час. На щастя, програмне забезпечення ГІС стає досить складним, щоб автоматично розпізнавати та об'єднувати різні системи координат.
2.23. Характеристики зони UTM
На малюнку нижче зображена область, покрита єдиною зоною сітки системи координат UTM. Кожна зона UTM охоплює 6° довготи, з 84° півночі та 80° півдня. Зони звужуються від 666 000 метрів в «ширину» на екваторі (де 1° довготи становить близько 111 кілометрів в довжину) до лише близько 70 000 метрів на 84° півночі і близько 116 000 метрів на 80° на південь. Полярні області покриті полярними системами координат. Кожна зона UTM підрозділяється уздовж екватора на дві половини, північну і південну.
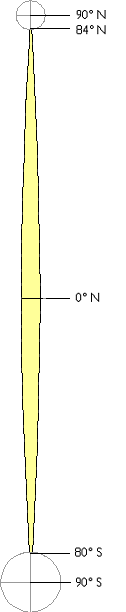
Обсяг однієї зони сітки системи координат UTM. Зверніть увагу, що хоча широти використовуються для визначення ступеня саме по відношенню до земної кулі, вони є географічними, а не UTM, координатами.
На ілюстрації нижче показано, як координатні сітки UTM відносяться до зони покриття, проілюстрованої вище. Північна і південна половини показані пліч-о-пліч для порівняння. Кожній половинці присвоюється своє походження. Походження північної південної зони розташовані на південь і захід від зони. Витоки північної зони розташовані на екваторі, 500 000 метрів на захід від центрального меридіана. Походження розташовуються так, що кожне значення координат у кожній зоні є додатним числом. Це мінімізує ймовірність помилок при розрахунках відстані і площі. За визначенням обидва витоки розташовані в 500 000 метрів на захід від центрального меридіана зони (іншими словами, схід центрального меридіана завжди становить 500 000 метрів E). Вони вважаються «помилковими» походженнями, оскільки вони розташовані поза зонами, до яких вони посилаються. Сходи UTM коливаються від 167,000 метрів до 833 000 метрів на екваторі. Ці діапазони звужуються до полюсів. Північні зони варіюються від 0 метрів до майже 9,400,000 в північних зонах і від трохи більше 1,000,000 метрів до 10,000,000 метрів у південних зонах. Зверніть увагу, що позиції на широтах, що перевищують 84° північ і 80° на південь, визначені в полярних стереографічних системах координат, які доповнюють систему UTM.
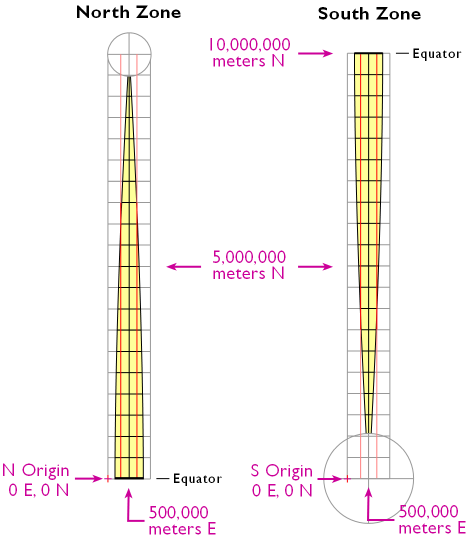
Характеристики зони системи координат UTM. Жовтий колір позначає області, в яких координати UTM дійсні для заданої зони. Червоні лінії, паралельні центральному меридіану, являють собою дві стандартні лінії, що використовуються в кожній поперечній проекції Меркатора. Кожна квадратна клітинка сітки на ілюстрації охоплює 500 000 метрів з кожного боку.
СПРОБУЙ ЦЕ!
ЗАСТОСУВАННЯ ПРАКТИКИ СИСТЕМИ КООРДИНАТ UTM
Чи готові ви спробувати свої сили в позиціонуванні в межах сітки системи координат UTM? Додаток Flash, пов'язане нижче, дозволяє перевірити свої знання. Додаток просить вас натиснути місця в зоні сітки, як зазначено випадково згенерованими координатами UTM.
Ви помітите, що програма дозволяє вибирати між легкими проблемами (в яких місця можливих рішень позначаються крапками) або більш важкими проблемами, які вимагають інтерполяції рішень. Ви можете вважати себе хорошими робочими знаннями географічної системи координат, якщо ви зможете вирішити принаймні шість «важких» завдань послідовно та за першим клацанням миші.
Натисніть тут, щоб запустити програму практики системи координат UTM. Якщо зона UTM не з'явилася після завантаження програми Flash, клацніть додаток правою кнопкою миші і виберіть у спливаючому меню пункт «Відтворити».
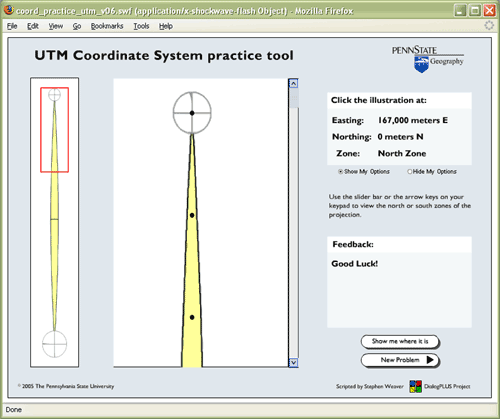
Примітка. Щоб виконати цю вправу, вам потрібно буде встановити програвач Adobe Flash. Якщо у вас ще немає Flash-плеєра, ви можете завантажити його безкоштовно на adobe.com
Дивіться Бібліографію (остання сторінка глави) для подальших читань про систему сітки UTM.
2.24. Національні мережі
Поперечна проекція Меркатора забезпечує основу для існуючих та запропонованих національних грід-систем у Великобританії та США.
У Великобританії топографічні карти, опубліковані в Ordnance Survey, відносяться до національної сітки площею 100 км, кожна з яких ідентифікується дволітерним кодом. Позиції в межах кожного квадрата сітки задаються з точки зору східних і північних напрямків між 0 і 100 000 метрів. Національна сітка Великобританії - це плоска система координат, яка базується на поперечній проекції Меркатора, центральний меридіан якої становить 2 західної довготи, зі стандартними меридіанами 180 км на захід і схід від центрального меридіана. Сітка, як правило, пов'язана з еліпсоїдом Airy 1830, відносинами, відомими як національна сітка (OSGB36®). Відповідними зонами UTM є 29 (центральний меридіан 9° на захід) та 30 (центральний меридіан 3° на захід). Однією з переваг національної сітки Великобританії над глобальною системою координат UTM є те, що вона усуває межу між двома зонами UTM.
Аналогічна система була запропонована для США Федеральним комітетом з географічних даних. Запропонована «Національна сітка США» є такою ж, як Військова система Grid Reference System (MGRS), всесвітня сітка, яка дуже схожа на систему UTM. Як пишуть Філ та Джуліанна Мюрке (1998, p.p. 229-230) у 4-му виданні Map Use, «військові [зокрема, Міністерство оборони США] прагнули мінімізувати плутанину при використанні довгих числових [UTM] координат», вказавши зони UTM та підзони літерами замість цифр. Як і система UTM, MGRS складається з 60 зон, кожна з яких охоплює 6° довготи. Кожна зона UTM підрозділяється на чотирикутники 19 MGRS 8° широти і один (чотирикутник від 72° до 84° північ) 12° широти. Літери C - X використовуються для позначення рядків комірок сітки з півдня на північ. I і O опущені, щоб уникнути плутанини з числами. Вікіпедія пропонує хороший запис на MGRS тут.
СПРОБУЙ ЦЕ!
ІНТЕРАКТИВНА ДЕМОНСТРАЦІЯ НАЦІОНАЛЬНОЇ СІТКИ ВЕЛИКОБРИТАНІЇ
Інформативна та весела демонстрація Національної сітки Великобританії опублікована британським дослідженням боєприпасів.
Примітка: Для перегляду цієї демонстрації вам потрібно буде встановити програвач Adobe Flash. Якщо у вас ще немає Flash-плеєра, ви можете завантажити його безкоштовно на adobe.com
ПРАКТИКА ВІКТОРИНИ
Зареєстровані студенти штату Пенн повинні повернутися зараз до папки Глава 2 в ANGEL (через меню Ресурси ліворуч), щоб пройти тест самооцінки про систему координат UTM.
Ви можете приймати практичні вікторини стільки разів, скільки хочете. Вони не забиваються і ніяк не впливають на вашу оцінку.
2.25. Система координат площини стану
Нижче показаний південно-західний кут топографічної карти масштабу 1:24 000, опублікованої Геологічною службою США (USGS). Зверніть увагу, що географічні координати (40 45′ N широти, 77° 52′ 30″ W довготи) кута вказані. Також показані, однак, галочки та мітки, що представляють дві плоскі системи координат, універсальну поперечну систему Меркатора (UTM) та систему координат стану площини (SPC). Кліщ з позначкою «1 970 000 ФУТІВ» являє собою лінію сітки SPC, яка проходить перпендикулярно до екватора і 1,970 000 футів на схід від походження Північної зони Пенсільванії. Походження лежить далеко на захід від цього листа карти. Інші лінії сітки SPC, звані «northings» (не показані на ілюстрації), проходять паралельно екватору і перпендикулярно SPC східних значень з кроком 10000 футів. На відміну від ліній довготи, СНК схід і північ прямі і не сходяться на полюсах Землі.

Південно-західний кут топографічної карти USGS, що показує сітки кліщів і міток для трьох різних систем координат, включаючи систему координат SPC. (USGS. «Чотирикутник Державного коледжу, Пенсільванія»)
Сітка SPC - це широко використовуваний тип геопросторової системи координат площини, в якій позиції задаються як східні (відстані на схід від початку) та на північ (відстані на північ від початку). Ви можете сказати, що сітка SPC, згадана на карті, проілюстрованій вище, є старшою версією системи сітки 1927 SPC, оскільки (а) схід і північ вказані в футах і (б) сітки засновані на північноамериканській датумі 1927 (NAD27). Зони 124, що складають систему координат державного літака 1983 року, засновані на NAD 83, і, як правило, використовують метричну систему для визначення східних та північних напрямків.
Державні координати площини часто використовуються для географічної прив'язки великих масштабів (малої площі) геодезичних та картографічних проектів, оскільки координати площини простіші у використанні, ніж широти та довготи для обчислення відстаней та площ. А оскільки зони SPC поширюються на відносно менші площі, менше помилок нараховується на позиції, відстані та області, обчислені координатами стану площини, ніж з координатами UTM.
У цьому розділі ви навчитеся:
- Опишіть характеристики системи SPC, включаючи картографічну проекцію, на якій вона базується; і
- Перетворення географічних координат в координати SPC
2.26. SPC Сітка і карти прогнози
Плоскі системи координат роблять вигляд, що світ плоский. Очевидно, що якщо ви вирівняєте всю земну кулю до плоскої поверхні, розміри та форми сухопутних мас будуть спотворені, як і відстані та напрямки між більшістю точок. Якщо ваша область інтересів досить мала, однак, і якщо ви її спритно розплющите, ви можете піти з мінімумом спотворень. Основна проблема проектування, з якою зіткнулися геодезисти, які тоді спроектували систему координат державної площини, полягала у встановленні зон системи координат, які були достатньо малими, щоб мінімізувати спотворення до прийнятного рівня, але досить великими, щоб бути корисними.
Державна система координат площини 1983 (SPC) складається з 124 зон, які охоплюють 50 штатів США. Як показано нижче, деякі держави покриті однією зоною, а інші розділені на кілька зон. Кожна зона базується на унікальній проекції карти, яка мінімізує спотворення в цій зоні до 1 частини в 10 000 або вище. Іншими словами, вимірювання відстані 10 000 метрів буде в гіршому випадку на один метр (не включаючи помилку приладу, людську помилку тощо). Частота помилок варіюється в кожній зоні, від нуля вздовж стандартних ліній проекції до максимуму в точках, найвіддаленіших від стандартних ліній. Помилки будуть нараховуватися зі швидкістю, набагато нижчою за максимальну в більшості місць у заданій зоні SPC. Зони SPC досягають кращої точності, ніж зони UTM, оскільки вони охоплюють менші площі, і тому менш сприйнятливі до спотворень, пов'язаних з проекцією.
Система координат державного літака США 1983 року складається з 124 зон (Дойл 2004). Кожна зона являє собою окрему площину системи координат. (Аляска і Гаваї не показані).
Більшість зон SPC засновані на поперечній проекції Mercator або Lambert Conformal карти Conformal, параметри якої (такі як стандартні лінії) і центральні меридіани) оптимізовані для кожної конкретної зони. «Високі» зони, такі як в штаті Нью-Йорк, Іллінойс та Айдахо, базуються на унікальних поперечних проекціях Меркатора, які мінімізують спотворення, виконуючи дві стандартні лінії північ-південь по обидва боки центрального меридіана кожної зони. «Широкі» зони, такі як у Пенсільванії, Канзасі та Каліфорнії, базуються на унікальних конформних конічних проекціях Ламберта, які проходять дві стандартні паралелі захід-схід через кожну зону. (Одна з зон Аляски заснована на «косою» варіанті проекції Меркатора. Це означає, що замість стандартних ліній, паралельних центральному меридіану, як у поперечному випадку, Косий Меркатор виконує дві стандартні лінії, які нахилені таким чином, щоб мінімізувати спотворення вздовж аляскинської панорами.)
Два типи картографічних проекцій мають властивість конформальності, що означає, що кути, нанесені в системі координат, рівні кутам, виміряним на поверхні Землі. Як ви можете собі уявити, конформність - корисна властивість для землевпорядників, які роблять своє житло вимірюванням кутів. (Геодезисти також вимірюють відстані, але, на жаль, немає проекції карти, яка може зберегти справжні відстані скрізь у площинній системі координат.) Розглянемо ці два типи картографічних проекцій коротко.
Як і більшість картографічних проекцій, поперечна проекція Меркатора насправді є математичним перетворенням. Ілюстрація нижче може допомогти вам зрозуміти, як працює математика. Концептуально поперечна проекція Меркатора переносить позиції на земній кулі у відповідні положення на циліндричній поверхні, яка згодом розрізається від кінця до кінця і сплющується. На ілюстрації циліндр дотичний до (торкається) земної кулі уздовж однієї лінії, стандартної лінії (конкретно, стандартного меридіана). Як показано на карті маленького світу поруч із земною кулею та циліндром, спотворення масштабу є мінімальним вздовж стандартної лінії і збільшується з відстанню від неї.
Еліпси спотворень, нанесені червоним кольором, допомагають нам візуалізувати закономірність спотворення масштабу, пов'язану з загальною поперечною проекцією Меркатора. Якби не сталося спотворень у процесі проектування карти, показаної нижче, всі еліпси були б однакового розміру та круглої форми. Як бачите, еліпси, нанесені уздовж центрального меридіана, мають все однаковий розмір і круглу форму. Далеко від центрального меридіана еліпси неухильно збільшуються в розмірах, хоча їх форми залишаються рівномірно круглими. Ця закономірність відображає той факт, що спотворення масштабу збільшується з відстанню від стандартної лінії. Крім того, еліпси показують, що характер спотворень, пов'язаний з цією проекцією, полягає в тому, що форми об'єктів, як вони з'являються на земній кулі, зберігаються, а їх відносні розміри спотворюються. Зберігаючи справжні кути, конформні проекції, такі як Меркатор (включаючи його поперечні та косі варіанти), також зберігають форми.

Концептуальна модель поперечної проекції карти Меркатора (ліворуч) та отриманої карти (праворуч). Товсті червоні лінії представляють лінію дотику між земною кулею і поверхнею проекції (циліндр), і відповідний стандартний меридіан на карті. Червоні кола на карті показують, що спотворення, введене в результаті проекції карти, збільшується з відстанню від стандартної лінії. На земній кулі всі кола були б однакового розміру.
Зони SPC, які мають тенденцію із заходу на схід (включаючи Пенсільванію), засновані на унікальних конформних конічних проекціях Ламберта. Замість циліндричної проекційної поверхні, що використовується проекціями, подібними до Меркатора, конформна конічна коніка Ламберта та проекції карти, подібні до неї, використовують конічні проекційні поверхні, як показано нижче. Зверніть увагу на дві лінії, на яких глобус і конус перетинаються. Обидва вони є стандартними лініями; зокрема, стандартні паралелі. Широти стандартних паралелей, вибраних для кожної зони SPC, мінімізують спотворення масштабу по всій цій зоні.
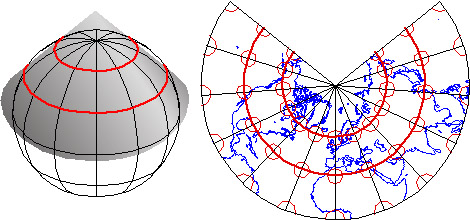
Концептуальна модель конформної конічної проекції Ламберта (ліворуч) та отриманої карти (праворуч). Дві товсті червоні лінії, що позначають перетину земної кулі та проекційної поверхні (конуса), відповідають двом стандартним паралелям на карті. Червоні кола на карті підтверджують, що масштаб карти рівний уздовж обох стандартних паралелей. Спотворення збільшується з відстанню від стандартних паралелей скрізь на проектованій карті і в системі координат, на якій вона заснована.
2.27. Характеристики зони SPC
За консультацією з різними державними установами Національна геодезична зйомка (NGS) розробила систему координат державної площини з кількома завданнями проектування на увазі. Головними серед них були:
- Плоскі координати для зручності використання при розрахунках відстаней і площ;
- Всі позитивні значення для мінімізації помилок розрахунку; і
- Максимальна похибка 1 частина в 10000.
Координати площини задають позиції в плоских сітках. Проекції карт потрібні для перетворення координат широти та довготи в координати площини. Дизайнери зробили дві речі, щоб мінімізувати неминучі спотворення, пов'язані з проекціями карт. По-перше, вони розділили США на 124 відносно невеликі зони. По-друге, вони використовували дещо різні формули проекції карт для кожної зони. Вигнуті пунктирні червоні лінії на ілюстрації нижче представляють дві стандартні паралелі, які проходять через кожну зону. Широти стандартних ліній є одним з параметрів конформної проекції Ламберта Conformal, який можна налаштувати для мінімізації спотворень всередині зони.
Позиції в будь-якій системі координат задаються відносно початку координат. Витоки зони SPC визначаються таким чином, щоб гарантувати, що кожен схід і північ у кожній зоні є позитивними числами. Як показано на ілюстрації нижче, походження SPC розташовані на південь від округів, включених до кожної зони. Витоки збігаються з центральним меридіаном проекції карти, на якому базується кожна зона. Значення східного та північного напрямку біля витоків не є 0, 0. Натомість східні значення визначаються як позитивні значення, достатньо великі, щоб гарантувати, що кожен схід у зоні також є позитивним числом. Наприклад, помилкове походження Північної зони Пенсільванії визначається як 600 000 метрів на схід, 0 метрів на північ. Схід походження варіюється від зони до зони від 200 000 до 8,000,000 метрів на схід.
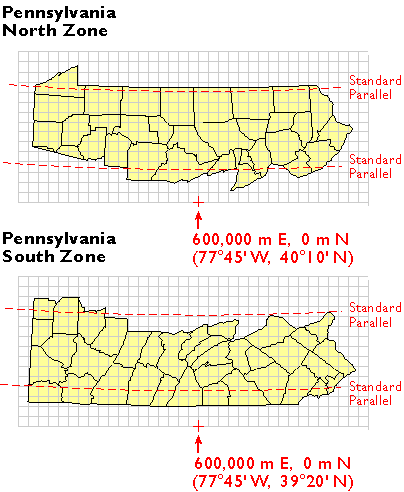
Схематичний вигляд двох зон системи координат державного площини, що показує округи, що складають кожну зону (жовтим кольором), походження кожної зони та стандартні паралелі проекцій карти, на яких засновані зони, вздовж яких спотворення масштабу дорівнює нулю.
Спробуйте це!
Дослідження місцевої зони сітки системи координат площини стану
У цьому занятті ви будете:
- Прочитайте частину авторитетного посібника з координат державного літака;
- Перегляньте позначення місцевої зони SPC (або потенційної зони, якщо ви з іншої країни, ніж США);
- Дослідити параметри проекції карти, на якій базується ваша локальна зона SPC; і
- Використовуйте веб-інструмент, наданий Національною геодезичною зйомкою США, щоб перетворити географічні координати в SPC.
Практична вікторина в кінці цього розділу допоможе вам оцінити ваше вільне володіння системою SPC.
1. Прочитайте вступ до Національного посібника з геодезичної зйомки Державна система координат площини 1983 року Джеймса Е. Стема (1990).
Перейдіть за цим посиланням, щоб завантажити посібник у форматі Portable Document Format (PDF). Читати сторінки 1-13 (сторінки 11-23 PDF-документа). Також див. Додаток А, починаючи з с. 62 (73), в якому перераховані проекції карт та інші параметри кожної зони.
2. Подивіться на місцеву зону SPC.
Головна сторінка інструментарію Національної геодезичної зйомки
- Відвідайте Геодезичний інструментарій NGS Національної геодезичної зйомки. Зверніть увагу на різні програми, які NGS підтримує для геодезичної та картографічної спільноти.
- Скористайтеся спадним меню, щоб перейти до інструмента «Координати площини стану».
- На сторінці «Координати площини стану» перейдіть за посиланням Інтерактивні конверсії з написом «Знайти зону».
- Подивіться свою місцеву зону SPC (або прийняту зону) за округом або посадою.
- Ви можете перевірити результат за допомогою списку Ріка Кінга або посібника Stem (1990), який ви завантажили раніше.
3. Перегляньте проекцію карти та походження сітки, на якій базується ваша місцева зона SPC.
- Зверніться до посібника Stem (1990), який ви завантажили раніше. Зокрема, див. Додаток А, стор. 63-72 (73-83). На якій проекції карти базується ваша локальна (або прийнята) зона?
- Зверніть увагу, що додаток повідомляє центральний меридіан і масштабний коефіцієнт для кожної зони, яка базується на поперечній проекції Меркатора. Стандартні паралелі наведено для зон на основі конформної конічної проекції Ламберта. У посібнику Stem (1990) «масштабний коефіцієнт» виражається в терміні максимальної похибки вимірювання, пов'язаної з кожною зоною.
- Додаток А також перераховує координати SPC кожної зони походження, а також відповідні географічні координати.
4. Використовуйте NGS Toolkit для перетворення географічних координат в координати SPC.
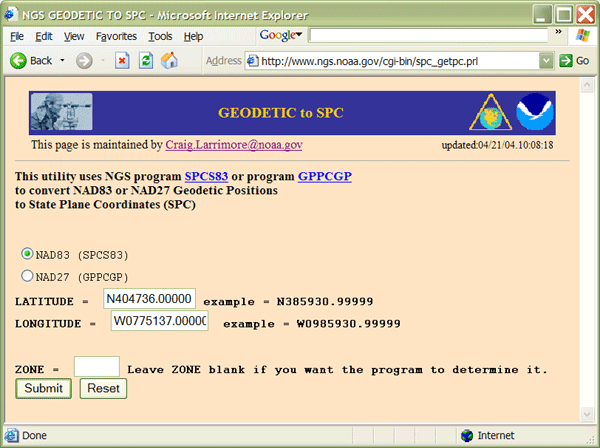
Національна геодезична зйомка Державна площина координати інструментарій доступний тут.
- Вам потрібно знати географічні координати цікавого місця, щоб завершити цю частину діяльності. Щоб переглянути широту та довготу, пов'язані з назвою США, відвідайте Інформаційну систему географічних назв USGS. Якщо ви не проживаєте в США, використовуйте Тезаурус географічних назв Гетті. Зверніть увагу; обов'язково виберіть правильний екземпляр назви місця. Міста та селища перераховані як «Населені місця» в Інформаційній системі географічних назв та як «Населені місця» в Тезаурусі Гетті.
- Повернутися до геодезичного інструментарію NGS Національної геодезичної зйомки.
- Скористайтеся спадним меню, щоб перейти до інструмента «Координати площини стану».
- На сторінці «Координати площини стану» перейдіть за посиланням Інтерактивні перетворення з написом «Широта/Довгота -> SPC»
- Вкажіть географічні (так звані «геодезичні») координати у форматі градусів-хвилин-секунд. Вам не потрібно показувати п'ять знаків праворуч від десяткової коми, як у прикладі, проілюстрованому вище, але вам потрібно додати десяткову крапку в кінці вхідних значень DMS; інструмент дозволяє ввести значення DMS, яке є точним до дробів секунди і так запрограмовано очікувати десяткової крапки.
- Правильний результат буде включати SPC Northing, Easting, зона, збіжність (поправочний коефіцієнт для розрахунків відстані, який компенсує тенденцію меридіанів до сходжень до полюсів), і масштабний коефіцієнт у вказаній точці.
Практика вікторини
Зареєстровані студенти штату Пенн повинні повернутися зараз до папки Глава 2 в ANGEL (через меню Ресурси ліворуч), щоб пройти тест самооцінки про систему координат стану площини.
Ви можете приймати практичні вікторини стільки разів, скільки хочете. Вони не забиваються і ніяк не впливають на вашу оцінку.
2.28. Картографічні прогнози
Координати широти та довготи визначають розташування точок у сітці системи координат, яка підходить до сфери або еліпсоїда, що наближається до форми та розміру Землі. Для відображення великих географічних областей на сторінці або екрані комп'ютера, а також найбільш ефективно обчислювати відстані, площі та інші величини, необхідно вирівняти Землю.

Картографічні проекції - це математичні рівняння, які перетворюють географічні координати (умовно позначаються грецькими символами лямбда для довготи і phi для широти) в координати площини (x і y). Якщо всі необхідні параметри відомі, зворотні проекційні рівняння можуть бути використані для перетворення проектованих координат назад в непроектовані географічні координати.
Географічні системи координат площини, такі як Універсальний поперечний Меркатор і системи координат стану площини (розглянуті в іншому місці в цьому уроці) створюються шляхом спочатку згладжування решітки, а потім накладання прямокутної сітки над сплющеною решіткою. Перший крок, перетворення сітки географічної системи координат з більш-менш сферичної форми на плоску поверхню, включає системи рівнянь, які називаються картографічними проекціями.
Існує безліч різних методів проекції карт. Хоча лише деякі широко використовуються у великомасштабному відображенні, використовувані параметри проекції сильно різняться. Очікується, що фахівці з геоінформаційних систем будуть достатньо обізнаними, щоб вибрати проекцію карти, яка підходить для конкретної мети відображення. Очікується, що такі професіонали зможуть розпізнати тип, кількість та розподіл геометричних спотворень, пов'язаних з різними проекціями карти. Мабуть, найголовніше, вони повинні знати про параметри картографічних проекцій, які повинні бути узгоджені для того, щоб об'єднати географічні дані з різних джерел. Наступні сторінки вводять ключові поняття. Однак ця тема занадто залучена, щоб освоїти один розділ однієї глави. Дійсно, штат Пенн пропонує цілий онлайн-курс на один кредит у «Проекції карт для геопросторових професіоналів» (GEOG 861). Якщо ви або плануєте стати професіоналом ГІС, ви повинні володіти хоча б однією хорошою книгою з проекцій карт. У бібліографії в кінці цього уроку випливає кілька рекомендацій. Якщо ви хочете запропонувати власну рекомендацію, будь ласка, додайте її як коментар до сторінки бібліографії.
Студенти, які успішно пройшли цей розділ, повинні мати можливість:
- Інтерпретувати діаграми спотворень для виявлення геометричних властивостей сфери, які зберігаються певною проекцією.
- Класифікуйте проектовані решітки за сімейством проекцій.
2.29. Геометричні властивості збережені та спотворені
Багато типів картографічних проекцій були розроблені відповідно до конкретних цілей. Жодна проекція не дозволяє нам згладити земну кулю, не спотворюючи його, однак. Еліпси спотворень допомагають нам візуалізувати, який тип спотворень викликала проекція карти, скільки спотворень відбулося і де воно сталося. Еліпси показують, як уявні кола на земній кулі деформуються в результаті певної проекції. Якби в процесі проектування карти, показаної нижче, не відбулося жодних спотворень, усі еліпси були б однакового розміру та круглої форми.
Коли позиції на решітці перетворюються на позиції на проектованій сітці, можуть виникати чотири типи спотворень: спотворення розмірів, кутів, відстаней та напрямків. Кажуть, що проекції карт, які уникають одного або декількох з цих типів спотворень, зберігають певні властивості земної кулі.
ЕКВІВАЛЕНТНІСТЬ
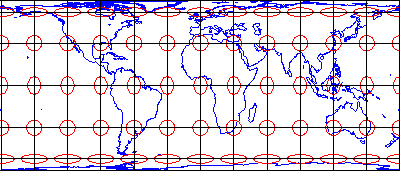
Так звані рівноплодні проекції підтримують правильні пропорції розмірів площ на земній кулі та відповідних областей на проектованій сітці (звичайно, допускаючи різницю в масштабі). Зверніть увагу, що форми еліпсів у проекції циліндричної рівної площі вище спотворюються, але області, які кожен з них займає, еквівалентні. Проекції рівних площ є кращими для дрібномасштабного тематичного картографування, особливо коли глядачі карт повинні порівнювати розміри об'єктів площі, таких як країни та континенти.
ВІДПОВІДНІСТЬ
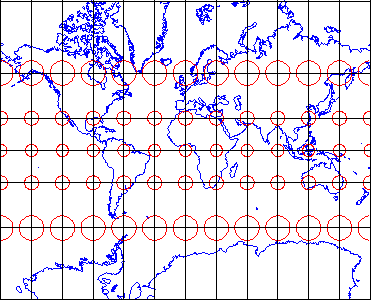
Еліпси спотворень, нанесені на конформній проекції, показаної вище, істотно різняться за розміром, але мають однакову круглу форму. Послідовні форми вказують на те, що конформні проекції (як ця проекція Меркатора світу) зберігають точність вимірювань кута від земної кулі до площини. Іншими словами, кут, виміряний землевпорядником в будь-якому місці поверхні Землі, може бути нанесений у відповідному місці на конформній проекції без спотворень. Це корисна властивість пояснює той факт, що конформні проекції майже завжди використовуються в якості основи для великомасштабної зйомки і картографування. Серед найбільш широко використовуваних конформних проекцій - поперечний Меркатор, Конформний конічний Ламберта та Полярний стереографічний.
Конформальність і еквівалентність є взаємовиключними властивостями. Тоді як проекції рівних площ спотворюють форми, зберігаючи точність розмірів, конформні проекції спотворюють розміри в процесі збереження форм.
РІВНОВІДДАЛЕНІСТЬ
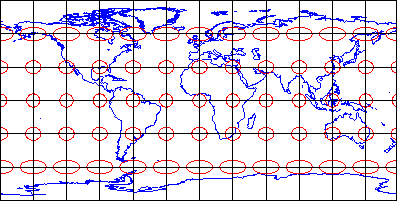
Рівновіддалені проекції карти дозволяють точно вимірювати відстані вздовж прямих ліній, що випромінюються лише з однієї або двох точок. Зверніть увагу, що еліпси, нанесені на циліндричній рівновіддаленій проекції (Plate Carrée), показаної вище, різняться як за формою, так і за розміром. Однак вісь північ-південь кожного еліпса має однакову довжину. Це показує, що відстані відповідають масштабу вздовж кожного меридіана; іншими словами, властивість рівновіддаленості зберігається від двох полюсів. Дивіться розділи 11 та 12 онлайн-публікації Відповідність проекції карти з необхідністю бачити, як можна налаштувати прогнози для полегшення вимірювання відстані та ефективного зображення діапазонів та кілець активності.
АЗИМУТАЛЬНІСТЬ
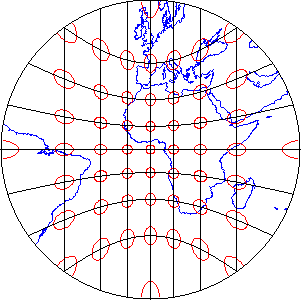
Азимутальні проекції зберігають напрямки (азимути) від однієї або двох точок до всіх інших точок на карті. Подивіться, як еліпси, нанесені на гномонічну проекцію, показану вище, змінюються за розміром і формою, але всі вони орієнтовані на центр проекції? У цьому прикладі це одна точка, в якій напрямки, виміряні на земній кулі, не спотворюються на проектованій решітці.
КОМПРОМІСУ
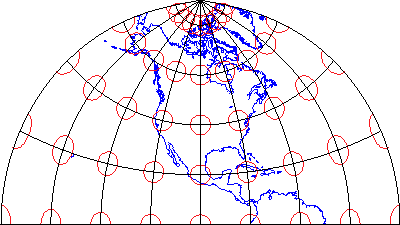
Деякі проекції карти не зберігають жодної з описаних вище властивостей, а натомість шукають компроміс, який мінімізує спотворення всіх видів. Приклад, показаний вище, є поліконічною проекцією, яка протягом багатьох років використовувалася Геологічною службою США в якості основи своєї серії топографічних чотирикутників, поки вона не була витіснена конформним поперечним Меркатором. Інший приклад - проекція Робінзона, яка часто використовується для дрібномасштабних тематичних карт світу.
ПРАКТИКА ВІКТОРИНИ
Зареєстровані студенти штату Пенн повинні повернутися зараз до папки Глава 2 в ANGEL (через меню Ресурси ліворуч), щоб пройти тест самооцінки про геометричні властивості проекцій карти.
Ви можете приймати практичні вікторини стільки разів, скільки хочете. Вони не забиваються і ніяк не впливають на вашу оцінку.
2.30. Класифікація методів проекції
Термін «проекція» має на увазі, що куляста сітка паралелей і меридіанів перетворюється, кидаючи свою тінь на якусь плоску або сплющену поверхню. Насправді майже всі методи проекції карт є математичними рівняннями. Аналогія оптичної проекції на плоску поверхню корисна, однак, як засіб класифікації дивного різноманіття проекційних рівнянь, розроблених за останні дві тисячі років і більше.
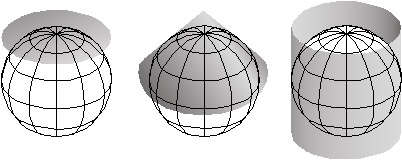
Три типи «сплющуються» поверхонь, на які може проектуватися решітка: площина, конус і циліндр.
Уявіть собі модель глобуса, який напівпрозорий, і містить яскраву лампочку. Уявіть, що світло буквально кидає тіні гратикули та форми материків на іншу поверхню, яка торкається земної кулі. Національне географічне товариство підготувало набір анімацій, які можуть допомогти вам візуалізувати аналогію.
Як ви могли собі уявити, зовнішній вигляд проектованої сітки буде досить сильно змінюватися залежно від типу поверхні, на яку вона проектується, і того, як ця поверхня вирівняна з земною кулею. Три поверхні, показані вище - площина у формі диска, конус та циліндр - представляють категорії, які складають більшість проекційних рівнянь, кодованих у програмному забезпеченні ГІС. Всі три показані в їх нормальних аспектах. Площина часто зосереджена на полюсі. Конус зазвичай вирівнюється з земною кулею таким чином, що його лінія зіткнення (дотичність) збігається з паралеллю в середніх широтах. І циліндр часто розташовується по дотичній до екватора (якщо він не повернутий на 90°, як це в поперечній проекції Меркатора). На наступних ілюстраціях показані деякі проектовані решітки, отримані проекційними рівняннями в кожній категорії.
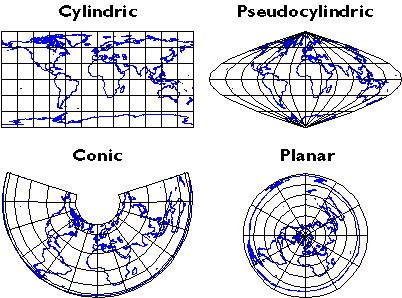
Чотири категорії картографічних проекцій
Циліндричні проекційні рівняння дають проектовані решітки з прямими меридіанами та паралелями, які перетинаються під прямим кутом. Наведений вище приклад - це циліндрична рівновіддалена (також звана плита Карре або географічна) у нормальному екваторіальному аспекті.
Псевдоциліндричні проекції - це варіанти на циліндриках, в яких меридіани вигнуті. Результат синусоїдальної проекції показаний вище.
Конічні проекції дають прямі меридіани, які сходяться до однієї точки на полюсах, паралелі, які утворюють концентричні дуги. Наведений вище приклад є результатом конічної рівної площі Альберса, яка часто використовується для тематичного відображення областей середньої широти.
Планарні проекції також дають меридіани, які є прямими і збіжними, але паралелі утворюють концентричні кола, а не дуги. Планарні проекції також називають азимутальними, оскільки кожна планарна проекція зберігає властивість азимутальності. Проектована решітка, показана вище, є результатом азимутальної рівновіддаленої проекції в її нормальному полярному аспекті.
Зовнішність може бути оманливою. Важливо пам'ятати, що вигляд проектованої решітки залежить від декількох параметрів проекції, включаючи широту початку проекції, центральний меридіан, стандартну лінію (и) та інші. Індивідуальні проекції карт можуть виглядати зовсім не так, як описані вище архетипи.
СПРОБУЙ ЦЕ!
Джон Снайдер та Філ Voxland (1994) опублікували альбом проекцій карт, який описує та ілюструє багато інших прикладів у кожній категорії проекцій. Витяги з цієї важливої роботи включені в наш Інтерактивний альбом проекцій карт, який зареєстровані студенти використовуватимуть для завершення проекту 1. Інтерактивний альбом доступний тут. Різноманітність доступних проекцій, а також здатність користувачів маніпулювати параметрами проекції обмежується можливостями програмної платформи ArcIMS, на якій ми розробили Інтерактивний альбом.
Flex Projector - це безкоштовна програма з відкритим вихідним кодом, розроблена на Java, яка підтримує набагато більше проекцій та змінних параметрів, ніж інтерактивний альбом. Бернхард Дженні з Інституту картографії ETH Zurich створив програму за сприяння Тома Паттерсона з Служби національних парків США. Ви можете завантажити проектор Flex з flexprojector.com
Ті, хто бажає вивчити проекції карт в більшій глибині, ніж це можливо в цьому курсі, можуть захотіти відвідати інформаційну сторінку, опубліковану Міжнародним інститутом геоінформаційних наук та спостереження Землі (Нідерланди), який відомий під спадковою абревіатурою ITC.
ПРАКТИКА ВІКТОРИНИ
Зареєстровані студенти штату Пенн повинні повернутися зараз до папки Глава 2 в ANGEL (через меню Ресурси ліворуч), щоб пройти самооцінку вікторини про класифікацію проекцій карт.
Ви можете приймати практичні вікторини стільки разів, скільки хочете. Вони не забиваються і ніяк не впливають на вашу оцінку.
2.31. Резюме
На цьому уроці ми дослідили кілька конотацій терміна шкали. Масштаб є синонімом сфери, коли він використовується для опису ступеня явища. У цьому сенсі «великий масштаб» означає «велика площа». Однак фахівці з географічної інформації часто використовують цей термін інакше. Масштаб карти відноситься до відносних розмірів об'єктів на карті та відповідних об'єктів на землі. У цьому контексті «великий масштаб» має на увазі «малу площу». Великий масштаб також передбачає більшу деталізацію та більшу точність, важливий момент, який слід пам'ятати при використанні карт як джерел для баз даних ГІС. Масштаб карти визначається математично як пропорція відстані карти до відстані землі. Сподіваюся, тепер ви готові використовувати рівняння масштабу для обчислення масштабу карти.
Масштаб також можна розглядати як опорну систему для вимірювання. Місця на земній кулі задаються з прив'язкою до географічної системи координат широт і довгот. Координати площини часто віддають перевагу географічним координатам, оскільки вони полегшують обчислення відстані, площі та інших величин. Географічні системи координат площини, такі як UTM та SPC, встановлюються спочатку згладжуванням решітки, а потім накладенням сітки координат площини. Математичні рівняння, що використовуються для перетворення географічних координат в координати площини, називаються картографічними проек Сітки площини та географічної системи координат пов'язані з наближеннями розміру та форми Землі, які називаються еліпсоїдами. Відносини між сітками і еліпсоїдами називаються горизонтальними датумами.
Горизонтальна база є невловимою концепцією для багатьох практиків ГІС. Відносно легко візуалізувати горизонтальну опорну точку в контексті непроектованих географічних координат. Просто перетягніть сітку широти та довготи над еліпсоїдом, і там є ваша горизонтальна база. Однак важче думати про датум в контексті проектної координатної сітки, як UTM та SPC. Подумайте про це так: спочатку драпіруйте сітку широти та довготи на еліпсоїді. Потім спроектуйте цю сітку на поверхню двовимірної площини. Потім накладіть прямокутну сітку східних і північних напрямків над проекцією, використовуючи контрольні точки для геореєстрації сіток. Там у вас є - координатна сітка проекції, заснована на горизонтальній базі.
Численні системи координат, датуми та проекції карт використовуються у всьому світі. Оскільки нам часто потрібно поєднувати географічні дані з різних джерел, фахівці ГІС повинні мати можливість геореєстрації двох або більше наборів даних, які базуються на різних системах координат, датумах та/або проекціях. Перетворення, включаючи перетворення координат, перетворення бази та проекції карт, - це математичні процедури, що використовуються для вирівнювання різноманітних даних. Характеристики систем координат, датумів і проекцій, що розглядаються в цьому курсі, викладені в наступних таблицях.
Системи координат, на які посилаються в цьому курсі (використовуються багато інших національних та локальних систем)
| Система координат | Одиниці | Обсяг | проекційна основа |
|---|---|---|---|
| Географічні | Кути (виражаються у градусах, хвилинах, секундах або десяткових градусах). | Глобальний | Жоден |
| УТМ | Відстані (метри) | Близько глобальної (8430′ N, 80° 30′ S) | Унікальна поперечна проекція Меркатора для кожної з 60 зон |
| Координати стану площини | Відстані (метри в SPCS 83, фути в SPCS 27) | У.С. | Унікальна поперечна конформна конічна проекція Меркатора або Ламберта для кожної з 123 зон (плюс косий Меркатор для аляски) |
Датуми, на які посилаються в цьому курсі (використовуються багато інших національних та локальних систем)
| Датум | Горизонтальний або вертикальний | Оптимізовано для | Опорна поверхня |
|---|---|---|---|
| І 27 | Горизонтальний | Північна Америка | Кларк 1866 еліпсоїд |
| І 38 | Горизонтальний | Північна Америка | Еліпсоїд GRS 80 |
| ВІГИ 84 | Горизонтальний | Світ | WGS 84 еліпсоїд |
| НАВПІЛ 88 | Вертикальний | Північна Америка | Рівень моря вимірюється на прибережних приливних станціях |
Картографічні прогнози, на які посилаються в цьому курсі (використовуються багато інших національних та місцевих систем)
| Назва проекції | Властивості збережені | Клас | спотворення |
|---|---|---|---|
| Меркатор | Конформний | Циліндрична | Спотворення площі збільшується з відстанню від стандартної паралелі (зазвичай екватора) |
| Поперечний Меркатор | Конформний | Циліндрична | Спотворення площі збільшується з відстанню від стандартного меридіана |
| Ламберт Конформний конічний | Конформний | Конічний | Спотворення площі збільшується з відстанню від однієї або двох стандартних паралелей |
| Тарілка Карре (іноді називається «Географічна» проекція) | Рівновіддалений | Циліндрична | Спотворення площі та форми збільшується з відстанню від стандартної паралелі (зазвичай екватора) |
| Альберс рівної площі конічний | Еквівалент | Конічний | Спотворення форми збільшується з відстанню від однієї або двох стандартних паралелей |
Складено зі Снайдера, 1997
ВІКТОРИНА
Зареєстровані студенти штату Пенн повинні повернутися зараз до папки Chapter 2 в ANGEL (через меню «Ресурси» ліворуч), щоб пройти оцінену вікторину Chapter 2.
Це один враховує. Ви можете взяти оцінені вікторини лише один раз.
Мета оцінених вікторин полягає в тому, щоб переконатися, що ви уважно вивчили текст, що ви освоїли практичну діяльність, і що ви виконали навчальні цілі глави. Ви можете переглядати главу під час вікторини.
Після того, як ви надіслали вікторину та опублікували будь-які питання, які можуть виникнути на наших дискусійних форумах або сторінках глав, ви завершите главу 2.
КОМЕНТАРІ ТА ПИТАННЯ
Зареєстровані студенти можуть залишати коментарі, запитання та відповіді на запитання щодо тексту. Особливо вітаються анекдоти, які пов'язують текст глави з вашим особистим або професійним досвідом. Крім того, в системі управління курсами ANGEL доступні дискусійні форуми для коментарів і питань на теми, якими ви, можливо, не захочете ділитися з усім світом.
Щоб залишити коментар, прокрутіть вниз до текстового поля під «Опублікувати новий коментар» і почніть вводити текст у текстовому полі, або ви можете відповісти на існуючу гілку. Коли ви закінчите вводити текст, натисніть кнопку «Попередній перегляд» або «Зберегти» (Зберегти фактично надішле ваш коментар). Після того, як ваш коментар буде опублікований, ви зможете редагувати або видаляти його за потребою. Крім того, ви зможете відповісти на інші публікації в будь-який час.
Примітка: перші кілька слів кожного коментаря стають його «заголовком» у гілці.
2.32. Бібліографія
3-D Програмне забезпечення (2005). Картографічні проекції сторінок. Отримано 8 січня 2005 р., з http://www.3dsoftware.com/Cartography/
Американський конгрес з геодезії та картографування (п. д.). Північноамериканська дата 1983 року. Збірник праць, що описують планування та здійснення перебудови північноамериканської горизонтальної мережі. Монографія № 2.
Буркард, Р.К. та ін. (1959-2002). Геодезія для непрофесіонала. Отримано 29 жовтня 2003 року з веб-сайту Національного агентства зображень та картографування http://www.ngs.noaa.gov/PUBS_LIB/Geodesy4Layman/toc.htm
Хім-ядерні системи, Inc. (1993). Проміжний звіт про скринінг сайту: Етап другий — регіональна дискваліфікація. Харрісбург П.А.
Крісман Н. Вивчення геоінформаційних систем (2-е видання) . Нью-Йорк: Джон Вілі та сини.
Кларк, К. (1995). Аналітична та комп'ютерна картографія (2-е видання) . Верхня річка Сідло, Нью-Джерсі: Прентіс Холл.
Дана, П.Г. (1998). Огляд систем координат. Ремісничий проект географа. Отримано 25 червня 2004 року, з Університету Колорадо в Боулдері, факультет географії веб-сайту: www.colorado.edu/географія/gcraft/примітки/coordsys/coordsys.html
Дана, П.Г. (1999). Огляд геодезичних датумів. Ремісничий проект географа. Отримано 25 червня 2004 року, з Університету Колорадо в Болдері, Департамент географії Веб-сайт: www.colorado.edu/географія/gcraft/примітки/datum/datum.html
Дьюхерст, В.Т. (1990). NADCON: Застосування поверхонь, отриманих від мінімальної кривизни, при перетворенні позиційних даних з північноамериканської бази 1927 року до північноамериканської бази 1983 року. Технічний меморандум NOAA NOS NGS 50. Отримано 1 січня 2005 р., з http://www.ngs.noaa.gov/PUBS_LIB/NGS50.pdf
Дойл, Д. (2004, лютий). Геодезичний інструментарій NGS, частина 7: Обчислення координат площини стану. Журнал «Професійний геодезист», 24:, 34-36.
Голландський, С. Універсальна поперечна система Меркатора. Отримано 9 січня 2008 з www.uwgb.edu/голландських/польових методів/UTMsystem.htm
Федеральний комітет з географічних даних. (Грудень 2001 р.). Національна сітка США. Отримано 8 травня 2006 р., з http://www.fgdc.gov/standards/projects/FGDC-standards-projects/usng/fgdc_std_011_2001_usng.pdf
Хільдебранд, Б. Зворотна точка+. Отримано 1 січня 2005 р., зwww.tapr.org/~KH2Z/Дорожня точка/
Іліфф, Дж. Датуми та картографічні прогнози для дистанційного зондування, ГІС та геодезії. Кейтнесс, Шотландія: Видавництво Уіттлз. Поширюється в США за допомогою CRC Press.
Ларрімор, К. (2002). Геодезичний інструментарій NGS. Отримано 26 жовтня 2004 р., з www.ngs.noaa.gov/Інструменти
Мюрке, П.К., Мюрке, Дж. Використання карти (3-е изд.) . Медісон В.І.: Публікації JP.
Мюрке, П.К., Мюрке, Дж. Використання карти (4-е изд.). Медісон В.І.: Публікації JP.
Мулкаре, Д.М. (2004). Національний геодезичний інструмент NADCON. Журнал «Професійний геодезист», лютий, стор. 28-33.
Національна геодезична зйомка. (н.д.). Північноамериканська утиліта перетворення даних. Отримано квітень 2004 р., зwww.ngs.noaa.gov/інструменти/Nadcon/Nadcon.html
Національна геодезична зйомка. Зображення, створене з геоїдних хвиль 15'x15 ', що охоплюють планету Земля. Отримано 1999, зwww.ngs.noaa.gov/Geoid/Гео-індекс.html (з моменту виходу на пенсію).
Національна геодезична зйомка. Берегова та геодезична зйомка колекції історичних зображень. Отримано 25 червня 2004 р., зwww.photolib.noaa.gov/cgs/index.html
Національне географічне товариство (1999). Кругла земля, плоскі карти. Отримано 18 квітня 2006 р., зwww.nationalgeographic.com/особливості/2000/дослідження/проекції/index.html
Обстеження боєприпасів (2000). Національна інформація про мережу GPS. 7: Поперечні проекції карти Меркатора. Отримано 27 серпня 2004 р., зwww.gps.gov.uk/guide7.asp
Робінсон, А. та ін. (1995). Елементи картографії (5-е видання) . Нью-Йорк: Джон Вілі та сини.
Робінсон, А.Х. і Снайдер, Дж. П. (1997). Відповідність проекції карти до потреби. Отримано 8 січня 2005 року з Картографії та географічного інформаційного товариства та веб-сайту Університету штату Пенсільванія: https://courseware.e-education.psu.edu/projection/
Слокум, Т.А., Макмастер, Р.Б., Кесслер, Ф, К., і Говард, Х. Тематична картографія та візуалізація (2-е видання) . Верхня річка Сідло, Нью-Джерсі: Прентіс Холл.
Сміт, Дж. Р. (1988). Базова геодезія. Ранчо Кордова Каліфорнія: Орієнтир Підприємства.
Снайдер, Дж. П. (1987). Проекції карти: Робочий посібник (Професійний документ з геологічної служби США № 1395). Вашингтон, округ Колумбія: Друкарня уряду Сполучених Штатів.
Снайдер, Дж. П. (1987). Картографічні проекції: Робочий посібник. (Професійний папір USGS № 1395). Вашингтон, округ Колумбія: Геологічна служба США (електронні версії доступні за адресою Pubs.er.usgs.gov/Djvu/PP/PP_1395.pdf)
Снайдер, Дж. П. і Воксланд П.М. (1989). Альбом картографічних проекцій (Професійний документ Геологічної служби США № 1453). Вашингтон, округ Колумбія: Друкарня уряду Сполучених Штатів.
Снайдер, Дж. П. і Воксланд, П.М. (1994). Альбом картографічних проекцій. (Професійний папір USGS № 1453). Вашингтон, округ Колумбія: Геологічна служба США. (інформація про замовлення опублікована на сайті http://erg.usgs.gov/isb/pubs/factsheets/fs08799.html)
Стем, Дж. Е. Державна система координат площини 1983 року (NOAA Керівництво NOS NGS 5). Роквілл, Меріленд: Національний геодезичний інформаційний центр.
Великий масштабний експеримент з біосфери та атмосфери в Амазонії (1999, 1 липня). Отримано 12 липня 1999 р., зDAACL.esd.ornl.gov/LBA_CPTEC/(після виходу на пенсію).
Геологічна служба США (2001). Універсальна поперечна меркаторная сітка. Фактологічний лист 077-01. Отримано 30 червня 2004 року, зmac.usgs.gov/mac/isb/паби/інформаційні таблиці/fs07701.html (з моменту виходу на пенсію).
Геологічна служба США (2003). Національні стандарти картографічних програм. Отримано 29 жовтня 2005 року, зrockyweb.cr.usgs.gov/nmpstds/nmas647.html
USGS. «Чотирикутник державного коледжу» [карта]. 7,5-хвилинний ряд. Вашингтон, округ Колумбія: USGS, 1962.
Ван Серп, Дж. (2004). Основні координати ГІС. Бока-Ратон FL: CRC Прес.
Вікіпедія. Вільна енциклопедія. Світова геодезична система. Отримано 8 травня 2006 р., з http://en.Wikipedia.org/wiki/WGS84
Вольф, П.Р. & Брінкер, Р.К. (1994) Елементарна геодезія (9-е вид.). Нью-Йорк, Нью-Йорк: Харпер Коллінз.