Skip to main content
LibreTexts - Ukrayinska

3: Масштаб та прогнози

  1. Last updated
  2. Save as PDF
  • Page ID
    37847

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Масштаб та прогнози - це дві основні особливості карт, які зазвичай не отримують тієї уваги, яку вони заслуговують. Масштаб відноситься до того, як одиниці карти відносяться до реальних одиниць. Проекції стосуються методів і проблем, пов'язаних з перетворенням тривимірної (і свого роду кускової) землі в двовимірну карту.

    Цей розділ познайомить вас з:

    • Масштаб і способи розповісти користувачеві карти, що карта вимірює на землі
    • Проекційна механіка, види проекцій та їх характеристики

    До кінця цієї глави ви повинні мати можливість читати масштаби карт і визначити загальні проекції разом з їх основними ознаками та використанням.

    3.1 Масштаб

    Світ величезний. Земна поверхня має площу понад 500 мільйонів км 2 і будь-яка картина землі, яку ви можете легко перенести, може показати лише загальні обриси континентів і країн. Коли ми візуально представляємо область світу на карті, ми повинні зменшити його розмір, щоб вписатися в межі карти. Масштаб карти вимірює, наскільки об'єкти світу зменшуються, щоб поміститися на карті; точніше, масштаб карти показує пропорцію заданої відстані на карті до відповідної відстані на землі в реальному світі.

    Масштаб карти представлений представницьким дробом, графічним масштабом або словесним описом.


    Масштаби карти. Карта може мати репрезентативний дріб, графічний масштаб або словесний опис, які означають одне і те ж. [1]

    Представницька фракція. Найбільш часто використовуваною мірою масштабу карти є представницький дріб (РФ), де масштаб карти відображається у вигляді співвідношення. Коли чисельник завжди встановлений на 1, знаменник відображає, наскільки більша відстань у світі. На малюнку нижче показана топографічна карта з РФ 1:24 000, що означає, що одна одиниця на карті представляє 24 000 одиниць на землі. Представницька фракція є точною незалежно від того, які одиниці використовуються; РФ можна виміряти як 1 сантиметр до 24000 сантиметрів, один дюйм до 24,000 дюймів, або будь-яку іншу одиницю.


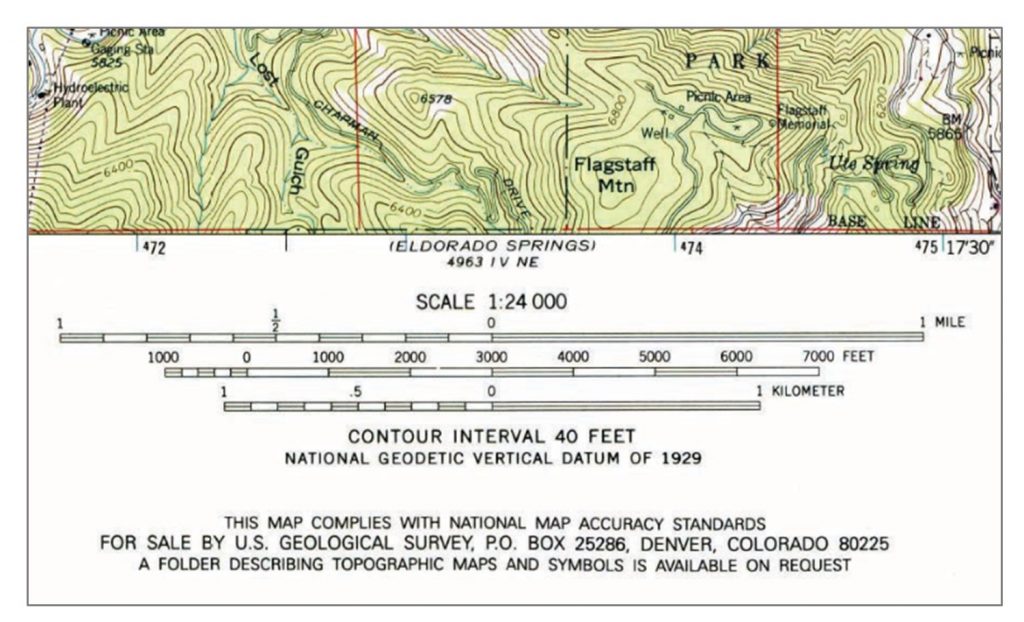
    Представницька фракція. Представницькі фракційні та масштабні смуги з топографічної карти Геологічної служби США (USGS). Ця топографічна карта має РФ 1:24 000, що означає, що одна одиниця на карті представляє 24 000 одиниць на землі. [2]

    Графічний масштаб. Масштабні смуги - це графічні зображення відстані на карті. Цифра має шкали для 1 милі, 7000 футів і 1 кілометр. Однією з важливих переваг графічних масштабів є те, що вони залишаються істинними, коли карти скорочуються або збільшуються.

    Словесний опис. Деякі карти, особливо старі, використовують словесний опис масштабу. Наприклад, зазвичай можна побачити «один дюйм являє собою один кілометр» або щось подібне написане на карті, щоб дати користувачам карти уявлення про масштаб карти.

    Виробники карт використовують масштаб для опису карт як маломасштабних або масштабних. Цей опис масштабу карти як великого чи малого може здатися спочатку неінтуїтивним. 3-метрова на 5-метрова карта Сполучених Штатів має невеликий масштаб карти, тоді як карта кампусу UMN такого ж розміру є великим -масштабом. Масштабні описи з використанням РФ забезпечують один із способів розгляду масштабу, оскільки 1:1000 більше 1:1 000 000. Іншими словами, якби ми змінили масштаб карти з РФ 1:100 000 так, щоб ділянка дороги була зменшена з однієї одиниці до, скажімо, 0,1 одиниці довжини, ми б створили карту меншого масштабу, представницька частка якої становить 1:1 000 000.

    Коли ми говоримо про великомасштабних і дрібномасштабних картах і географічних даних, то мова йде про відносні розміри і рівні деталізації ознак, представлених в даних. Загалом, чим більше масштаб карти, тим більше деталей, що показано.

    3.2 Ступінь проти роздільної здатності

    Обсяг карти описує область, видиму на карті, тоді як роздільна здатність описує найменшу одиницю, яка відображається. Ви можете думати про ступінь як опис регіону, до якого масштабується карта. Обсяг наведеної нижче карти є національною, оскільки вона охоплює суміжні Сполучені Штати, тоді як резолюція - це держава, оскільки держави - це найкращий рівень просторової деталізації, який ми можемо бачити.


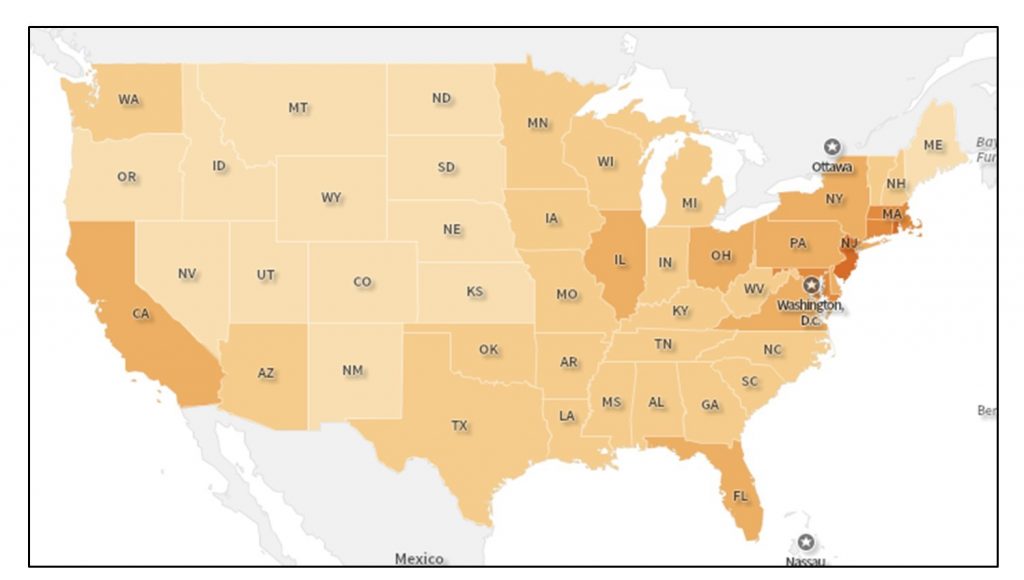
    Дозвіл та масштаб карти. Ця карта показує національний ступінь та державну резолюцію. Обсяг карти є національним, тоді як роздільна здатність знаходиться на державному рівні, оскільки вони є найкращим рівнем просторової деталізації, який ми можемо бачити. [3]

    Ми часто вибираємо роздільну здатність відображення навмисно, щоб зробити карту легшою для розуміння. Наприклад, якби ми намагалися відобразити карту з національною протяжністю у роздільній здатності блоків перепису, рівень деталізації був би настільки тонким, а межі були б настільки маленькими, що було б важко зрозуміти що-небудь про карту. Балансування ступеня та роздільної здатності часто є одним з найважливіших і складних рішень, яке повинен прийняти картограф. На малюнку нижче наведено ще два приклади різниці між ступенем та роздільною здатністю.


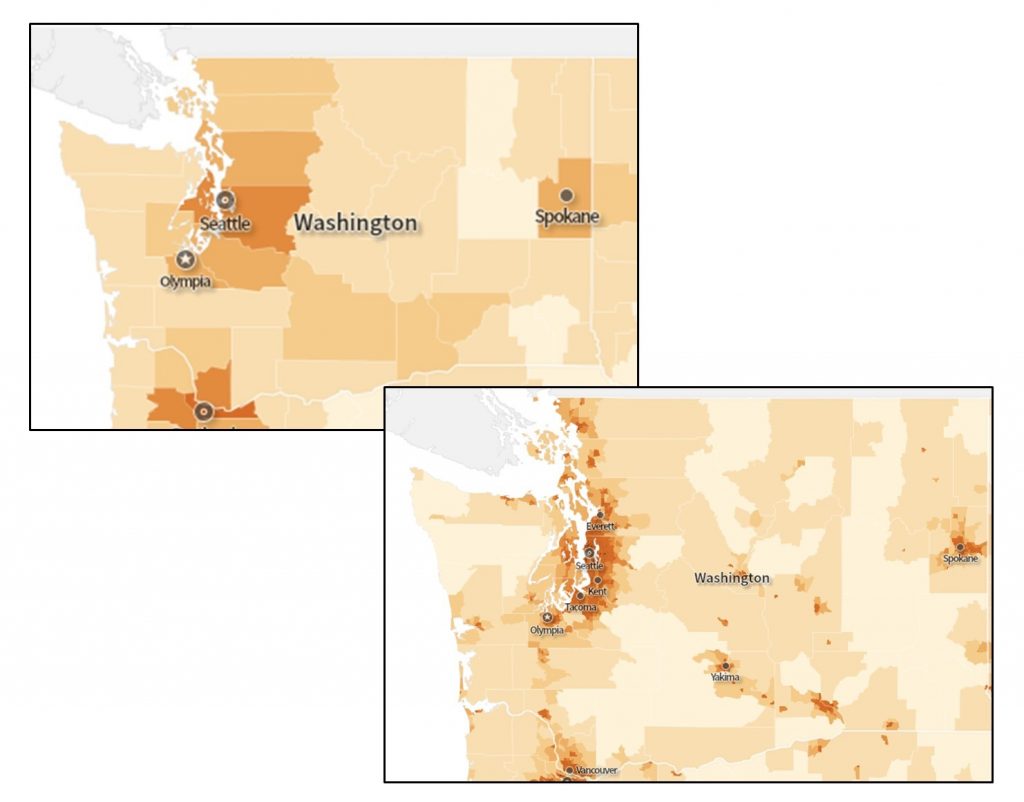
    Більше масштабу карти та роздільної здатності. Карти, що показують протяжність Тихоокеанського північного заходу. Верхнє зображення має просторову роздільну здатність округу, а нижнє має просторову роздільну здатність ділянок перепису. [4]

    3.3 Координати та прогнози

    Місця на земній поверхні вимірюються через координати, набір з двох і більше чисел, що визначає місце розташування по відношенню до якоїсь системи відліку. Найпростіша система такого роду - декартова система координат, названа на честь математика і філософа 17 століття Рене Декарта. Декартова система координат, подібна до наведеної нижче, - це просто сітка, утворена шляхом складання двох шкал вимірювань, однієї горизонтальної (x) та однієї вертикальної (y). Точка, в якій і x і y дорівнюють нулю, називається початком системи координат. На малюнку початок (0,0) розташовується в центрі сітки (перетин двох жирних ліній). Всі інші позиції вказуються відносно початку, як видно з точками в (3, 2) і (-4, -1)


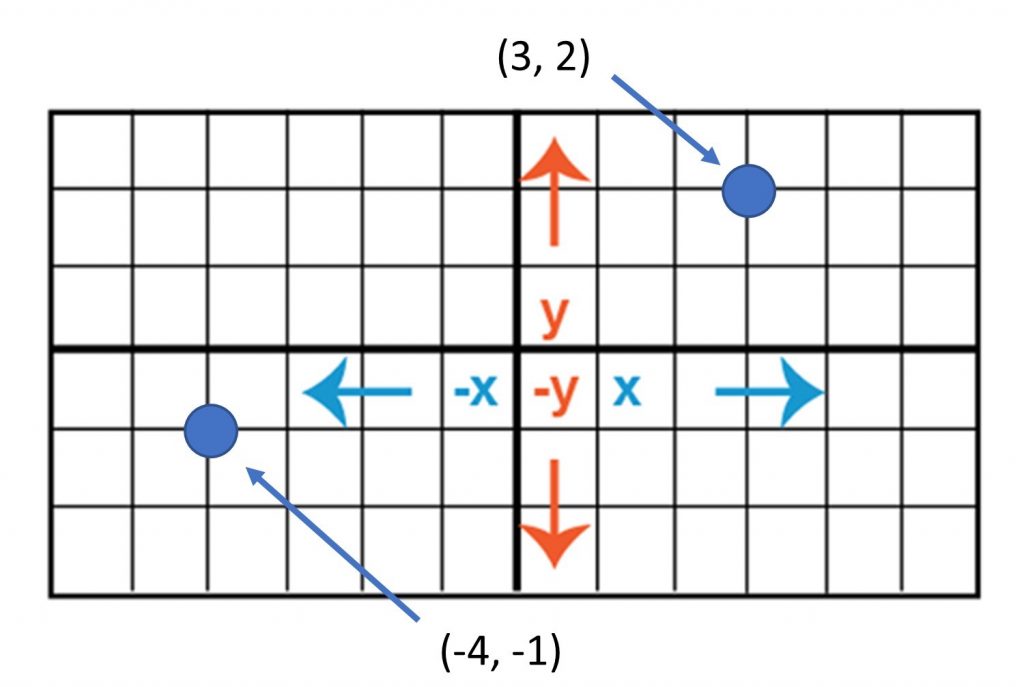
    Система координат. Місця розташування на поверхні Землі вимірюються через координати, набір з двох і більше чисел, що визначає місце розташування по відношенню до якоїсь системи відліку. [5]

    Географічна система координат розроблена спеціально для визначення положень на шорстко-сферичній поверхні Землі. Замість двох лінійних шкал вимірювання x та y, як у декартовій сітці, географічна система координат використовує шкалу схід-захід, яка називається довготою, яка коливається від +180° до -180°. Оскільки Земля кругла, +180° (або 180° E) та -180° (або 180° W) є тією ж лінією сітки, яка називається Міжнародною лінією дати. Навпроти Міжнародної лінії дат знаходиться простий меридіан, лінія довготи визначена як 0°. Шкала північ-південь, яка називається широтою, коливається від +90° (або 90° с.ш.) на північному полюсі до -90° (або 90° S) на Південному полюсі. Говорячи простою мовою, довгота визначає позиції на схід і захід, а широта визначає позиції на північ і південь. У більш високих широтах довжина паралелей зменшується до нуля на 90° півночі та півдня. Лінії довготи не паралельні, а сходяться до полюсів. Таким чином, хоча ступінь довготи на екваторі дорівнює відстані близько 111 кілометрів, ця відстань зменшується до нуля на полюсах.


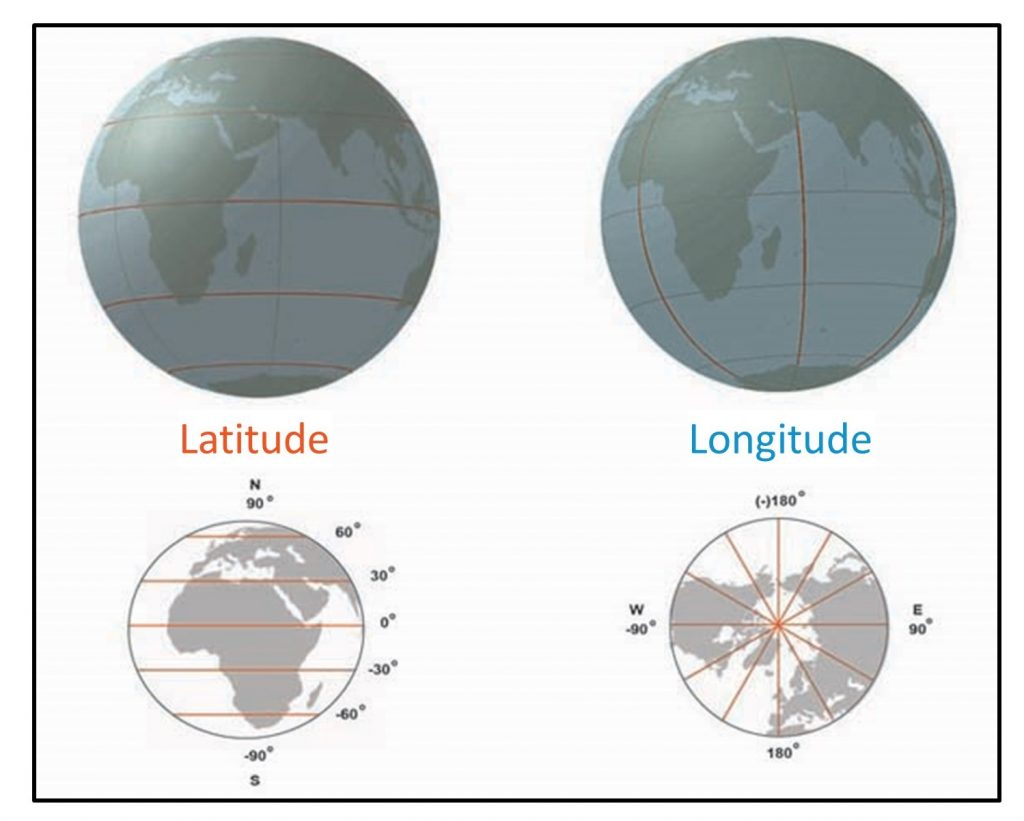
    Довгота і широта. Гратикула базується на шкалі схід-захід, яка називається довготою, і масштабі північ-південь, яка називається широтою. [6]

    Гратикуля визначає позиції на земній кулі з координатами широти та довготи. Гратикула відноситься до довготи і широти на тривимірному глобусі. Коли ми використовуємо довготу та широту на двовимірній карті, ми називаємо їх географічними координатами. Карти можуть мати величезний масив різних систем координат залежно від того, хто їх розробив і використовував.

    Проекція - термін перетворення тривимірного глобуса в двовимірну карту. Як зазначалося вище, гратикуля на глобусі корисна, але як ми можемо перейти від тривимірної решітки до двовимірних географічних координат, як показано на малюнку нижче? Ми обговоримо процес того, як об'єкти на тривимірній поверхні (землі) представляються на плоскому аркуші паперу або екрані комп'ютера. Наш акцент буде зроблений на властивостях, які різні проекції спотворюють або підтримують - площа, форма та відстань.


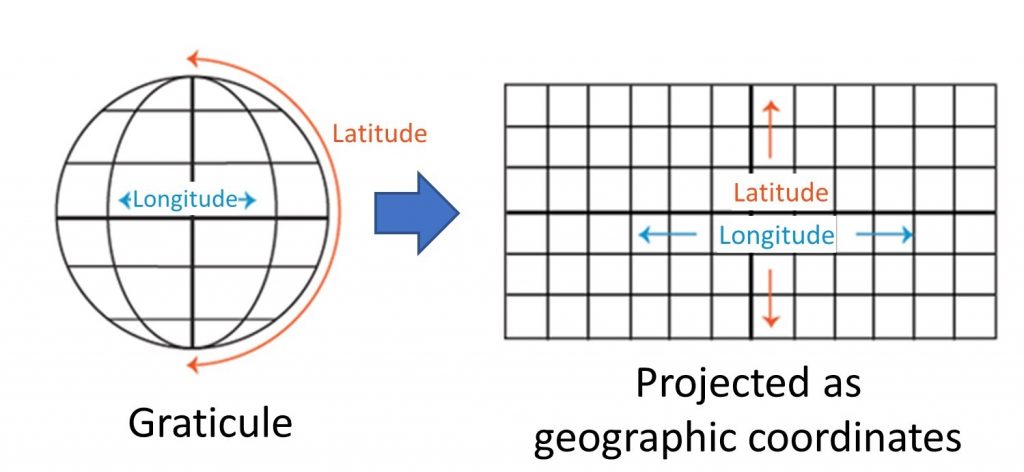
    Гратикула проектується. Довгота і широта гратикули стають двовимірними географічними координатами через проекцію. [7]

    Проекція - це процес складання двовимірної карти з тривимірного глобуса. Ми можемо думати про землю як про сферу. Насправді це більше еліпсоїд з кількома опуклостями, але добре думати про нього як про сферу. Щоб отримати уявлення про те, наскільки складним може бути цей процес, уявіть, як лущиться шкіра від апельсина і намагаючись укласти шкіру рівно.


    Сплющена апельсинова цедра. Ви можете собі уявити складність переходу з 3d на 2d поверхню, розглянувши, наскільки складно очистити шкірку від апельсина і спробувати укласти шкіру рівно. [8]

    У міру лущення і вирівнювання шкіри ви зіткнетеся з декількома проблемами:

    • Стрижка — розтягування шкіри в одному або декількох напрямках
    • Сльозотеча - змушує шкіру відокремлюватися
    • Компресування - змушує шкіру згущуватися і ущільнюватися

    Картографи стикаються з тими ж трьома проблемами, коли намагаються перетворити тривимірний глобус у двовимірну карту. Якби у вас був глобус, зроблений з паперу, ви могли б обережно спробувати «очистити» його в плоский аркуш паперу, але у вас був би великий безлад на руках. Натомість картографи використовують проекції для створення придатних двовимірних карт.


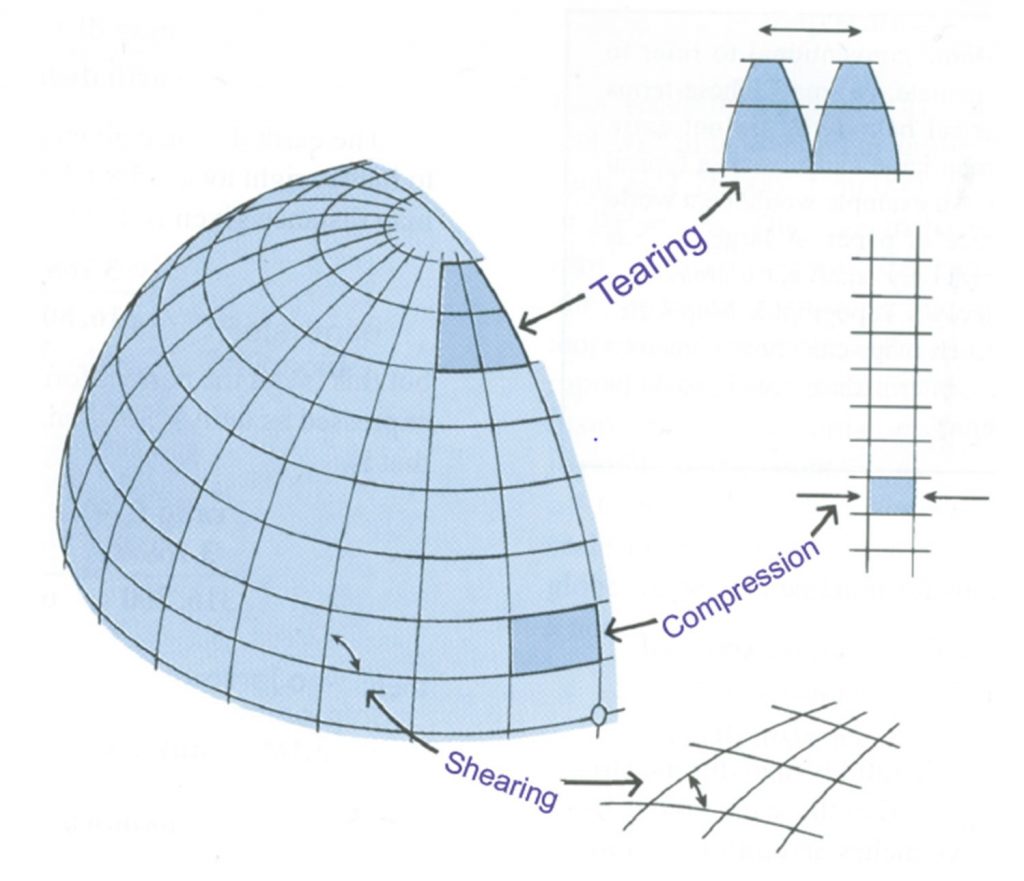
    Стрижка, розрив, стиснення. Картографи стикаються з цими трьома проблемами зсуву, розриву та стиснення на земній кулі, коли вони намагаються перетворити тривимірний глобус у двовимірну карту. [9]

    3.4 Механіка проекції

    Термін «проекція карти» позначає як процес, так і добуток перетворення просторових координат на тривимірній сфері в двовимірну площину. З точки зору фактичної механіки, більшість проекцій використовують математичні функції, які приймають як вхідні місця на сфері і переводять їх в місця на двовимірній поверхні.

    Корисно думати про прогнози в фізичному плані. Якби у вас був прозорий глобус розміром з пляжний м'яч і помістили світло всередині цього глобуса, він би кинув тіні на навколишню поверхню. Якби ця поверхня була аркушем паперу, яку ви обернули навколо земної кулі, ви могли б ретельно простежити ці тіні на папері, а потім згладити цей аркуш паперу і мати свою проекцію!


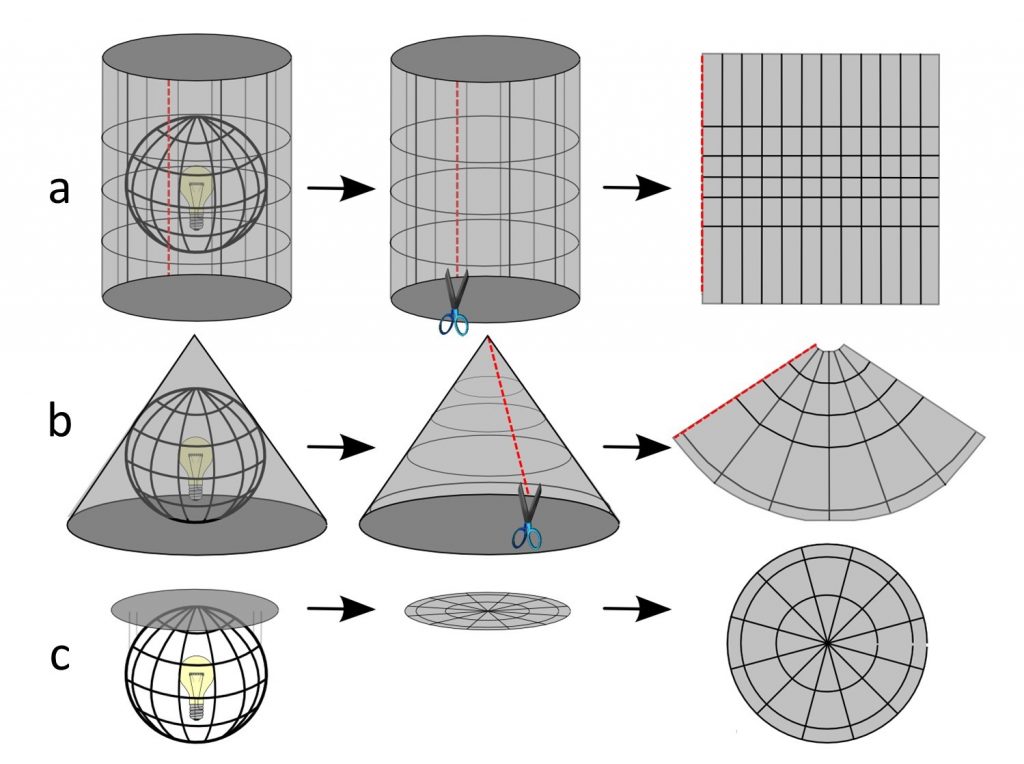
    Мислення проекцій у фізичному плані. Ви можете концептуалізувати проекцію як роботу з чітким глобусом, лампочкою та калькою. Якби у вас був прозорий глобус розміром з пляжний м'яч і помістили світло всередині цього глобуса, він би кинув тіні на навколишню поверхню. Ця поверхня може бути (а) циліндром, (б) конусом або (в) площиною. [10]

    Більшість проекцій перетворюють частину земної кулі на одну з трьох «розвиваються» поверхонь, так званих тому, що вони плоскі або можуть бути зроблені плоскими: площиною, конусом та циліндром. Отримані проекції називаються плоскими, конічними і циліндричними. Ми використовуємо поверхні, що розвиваються, оскільки вони усувають розриви, хоча вони будуть виробляти зсув і стиснення. З цих трьох проблем, розривання розглядається як найгірше, тому що ви б робити карти з усілякими дірами в них! Однак, як ми бачимо нижче, бувають випадки, коли ви можете створювати карти з розривами, і вони досить корисні.

    Місце, де розвиваюча поверхня торкається земної кулі, відоме як точка дотичної або дотичної лінії. Карти найбільш точно представлятимуть об'єкти на земній кулі в цих дотичних точках або лініях, при цьому спотворення збільшуються, коли ви рухаєтеся далі через зсув і стиснення. Саме з цієї причини циліндри часто використовуються для районів поблизу екватора, конуси, які використовуються для картографування середніх широт, а площини використовуються для полярних регіонів.


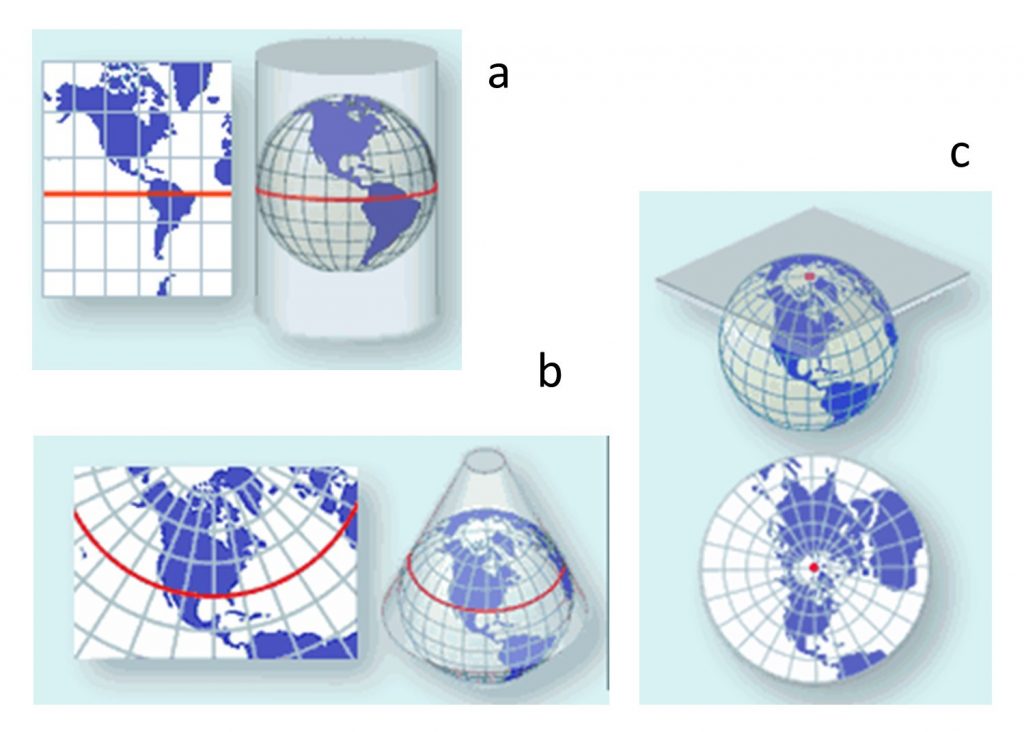
    Дотичність. Червоні лінії або точки позначають дотичну лінію або точку відповідно. Плоска поверхня торкається земної кулі, і це точка на проектованій карті, яка має найменше спотворення. місце, де розвиваюча поверхня торкається земної кулі, відоме як точка дотичної або дотичної лінії. Ці поверхні можуть бути (а) циліндром, (б) конусом або (в) площиною. [11]

    Для початківців картографістів розуміння точної механіки проекцій не має такого значення, як знання того, які властивості карти зберігаються або втрачаються з вибором проекції - тема наступного розділу.

    Проекції повинні спотворювати риси на поверхні земної кулі під час процесу їх плоскості, оскільки проекція передбачає зсув, розриви та стиснення. Оскільки жодна проекція не може зберегти всі властивості, виробник карт повинен знати, які властивості є найбільш важливими для їх призначення, і вибрати відповідну проекцію. Властивості, на яких ми зупинимося, є: форма, площа та відстань.

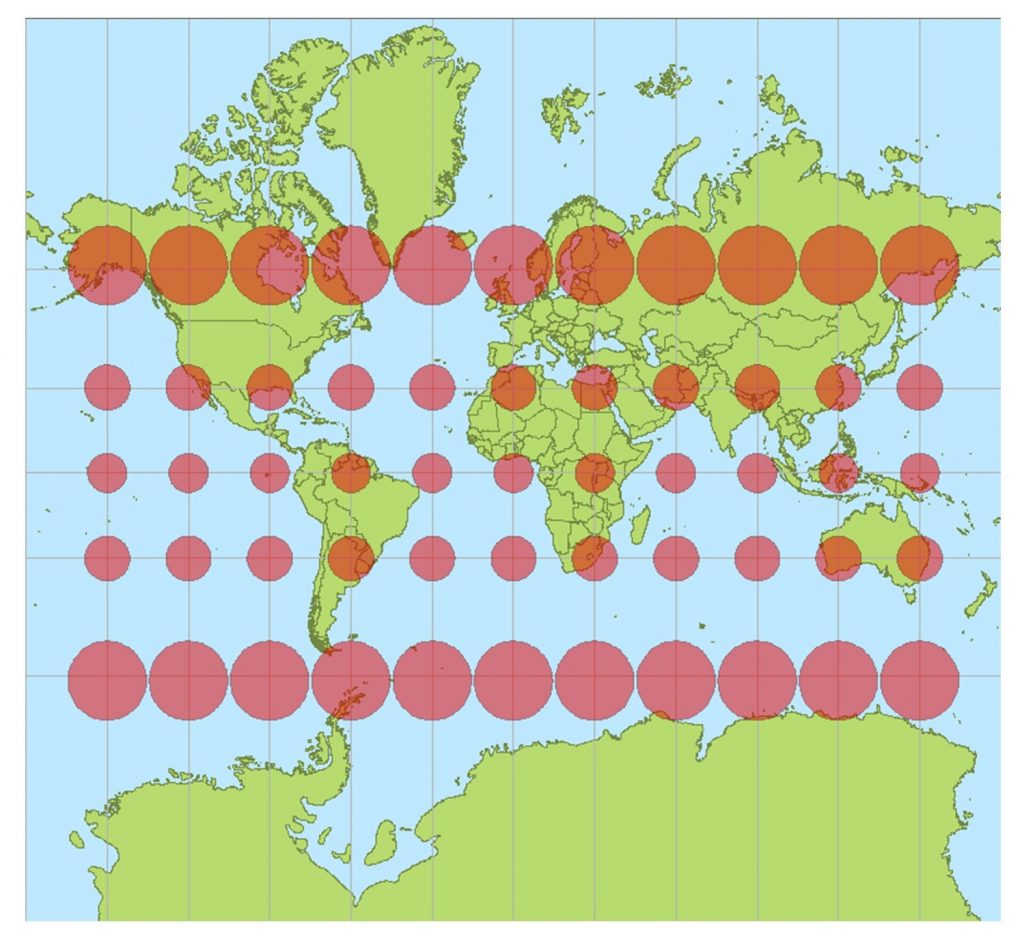
    Зверніть увагу, що спотворення не обов'язково пов'язане з типом поверхні, що розвивається, а скоріше до способу перетворення з цією поверхнею. Зберегти будь-яке з трьох властивостей можна за допомогою будь-якої з оброблюваних поверхонь. Один із способів погляду на проблему - це еліпси спотворень. Вони допомагають нам візуалізувати, який тип спотворень спричинила проекція карти, скільки спотворень відбулося та де воно сталося. Еліпси показують, як уявні кола на земній кулі деформуються в результаті певної проекції. Якби не було спотворень при проектуванні карти, всі еліпси були б однакового розміру та круглої форми.

    3.4.1 Конформний

    Конформні проекції зберігають форму і кут, але сильно спотворюють область в процесі. Наприклад, при проекції Меркатора форми берегових ліній точні на всіх ділянках карти, але країни біля полюсів виглядають набагато більшими щодо країн поблизу екватора, ніж вони є насправді. Наприклад, Гренландія становить лише 7-відсоткову площу суші Африки, але вона, здається, така ж велика!


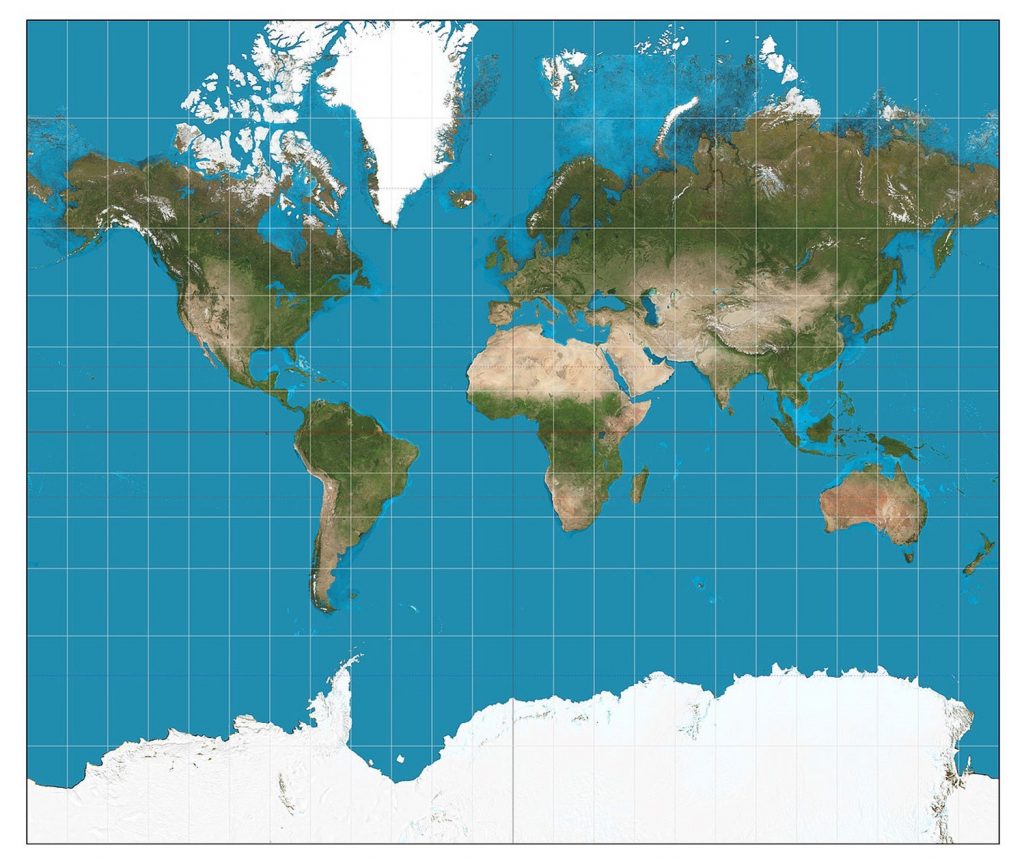
    Проекція Меркатора. Проекція Меркатора конформна, оскільки зберігає форму та кут, але сильно спотворює площу. [12]

    Конформні проекції слід використовувати, якщо основне призначення карти передбачає вимірювання кутів або представлення форм об'єктів. Вони дуже корисні для навігації, топографії (висоти) та карт погоди.


    Проекція Меркатора. Однією з перших карт світу була розроблена Меркатором (Carta do Mundo de Mercator, 1569). [13]

    Конформна проекція матиме еліпси спотворень, які істотно різняться за розміром, але мають однакову круглу форму. Послідовні форми вказують на те, що конформні проекції (як ця проекція світу Меркатора) зберігають форми та кути. Це корисна властивість пояснює той факт, що конформні проекції майже завжди використовуються в якості основи для великомасштабної зйомки і картографування.


    Спотворення Меркатора. Проекція Меркатора конформна, оскільки зберігає форму та кут, але сильно спотворює площу. [14]

    3.4.2 Рівна площа

    На рівноплотних проекціях розмір будь-якої площі на карті знаходиться в істинній пропорції її розміру на землі. Іншими словами, форми країн можуть здатися розчавленими або розтягнутими порівняно з тим, як вони виглядають на земній кулі, але їх площа суші буде точною відносно інших сухопутних мас. Наприклад, в проекції Галла-Петерса форма Гренландії значно змінена, але розміри її площі правильні в порівнянні з Африкою. Цей тип проекції важливий для кількісних тематичних даних, особливо для щільності відображення (атрибут над площею). Наприклад, це було б корисно для порівняння щільності сирійських біженців на Близькому Сході або кількості сільськогосподарських угідь у виробництві.


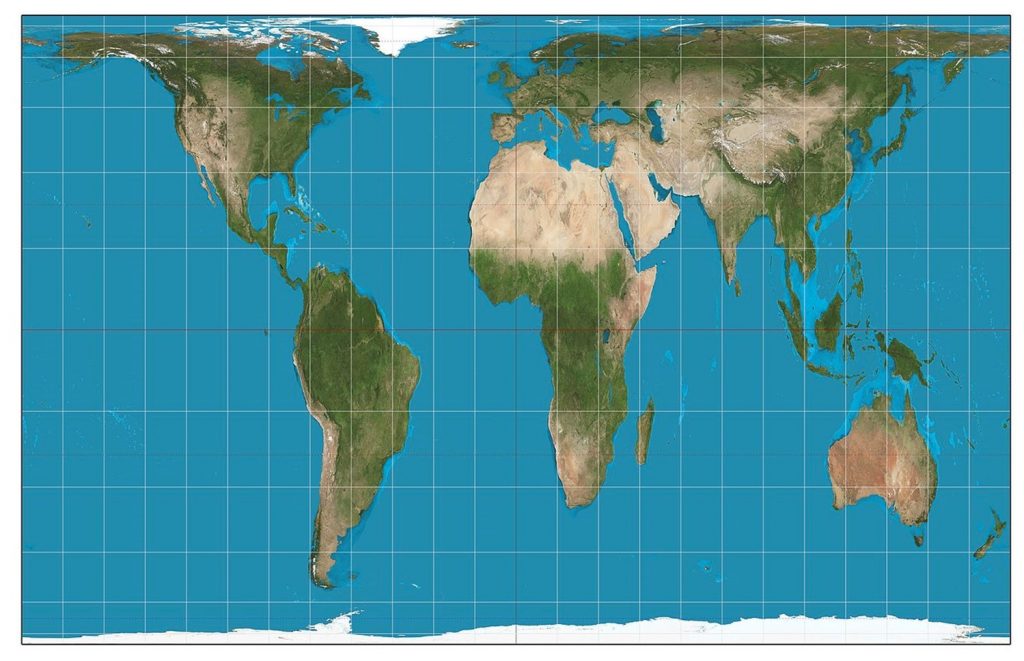
    Проекція Галла-Петерса. Проекція Галла Петерса дорівнює площі. Зверніть увагу, як форма Гренландії значно змінена, але розмір її площі є правильним порівняно з іншими регіонами, такими як Африка. [15]

    Однак, як ми бачимо при проекції рівної площі, еліпси зберігають правильні пропорції розмірів областей на земній кулі, але їх форми спотворюються. Проекції рівних площ є кращими для дрібномасштабного тематичного картографування, особливо коли користувачі карт повинні порівнювати розміри об'єктів площі, таких як країни та континенти.


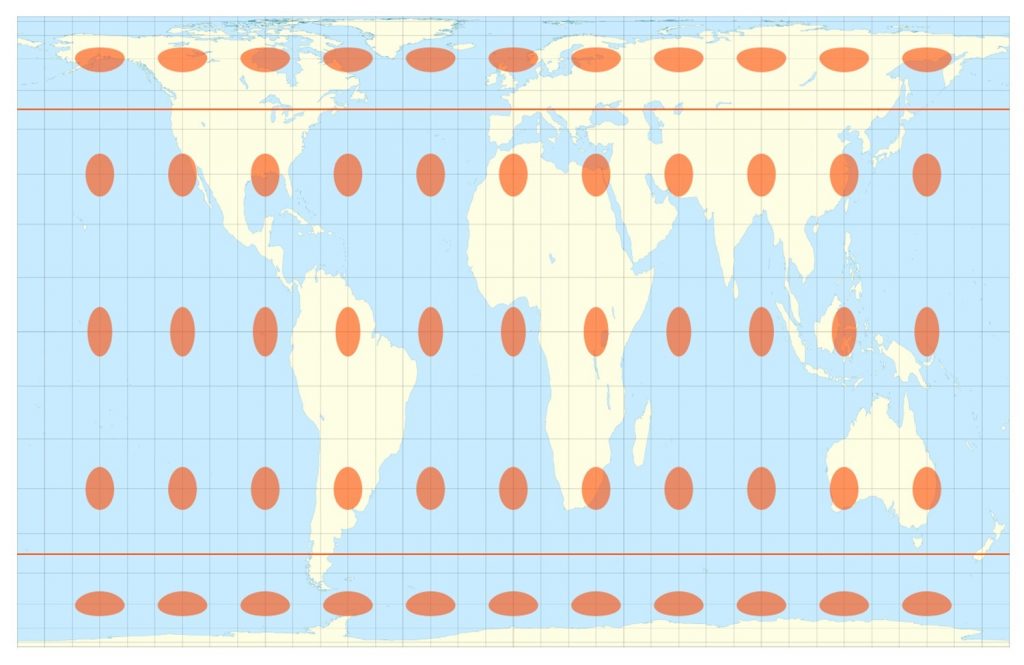
    Викривлення Галла-Петерса. Проекція Галла Петерса дорівнює площі. Зверніть увагу, як форма Гренландії значно змінена, але розмір її площі є правильним порівняно з іншими регіонами, такими як Африка. [16]

    3.4.3 Рівновіддалений

    Рівновіддалені проекції, як випливає з назви, зберігають відстань. Це трохи вводить в оману, оскільки жодна проекція не може підтримувати відносну відстань між усіма місцями на карті. Рівновіддалені карти здатні, однак, зберігати відстані за кількома чітко зазначеними лініями. Наприклад, на азимутальної рівновіддаленій проекції всі точки є пропорційно правильною відстанню і напрямком від центральної точки. Цей тип проекції буде корисним візуалізації шляхів польоту літака від одного міста до кількох інших міст або в картографуванні епіцентру землетрусу. Азимутальні проекції зберігають відстань за рахунок спотворення форми і площі в деякій мірі. Прапор Організації Об'єднаних Націй містить приклад полярної азимутальної рівновіддаленої проекції.


    Азимутальна рівновіддалена проекція. У цій рівновіддаленій проекції всі точки є пропорційно правильною відстані та напрямку від центральної точки. Ця проекція використовується на карті Організації Об'єднаних Націй. [17]

    3.4.4 Компромісні, перервані та художні проекції

    Деякі проекції, включаючи проекцію Робінсона, дотримуються балансу між різними властивостями карти. Іншими словами, замість того, щоб зберігати форму, площу або відстань, вони намагаються уникнути крайніх спотворень будь-якого з цих властивостей. Цей тип проекції буде корисним для загальної карти світу.


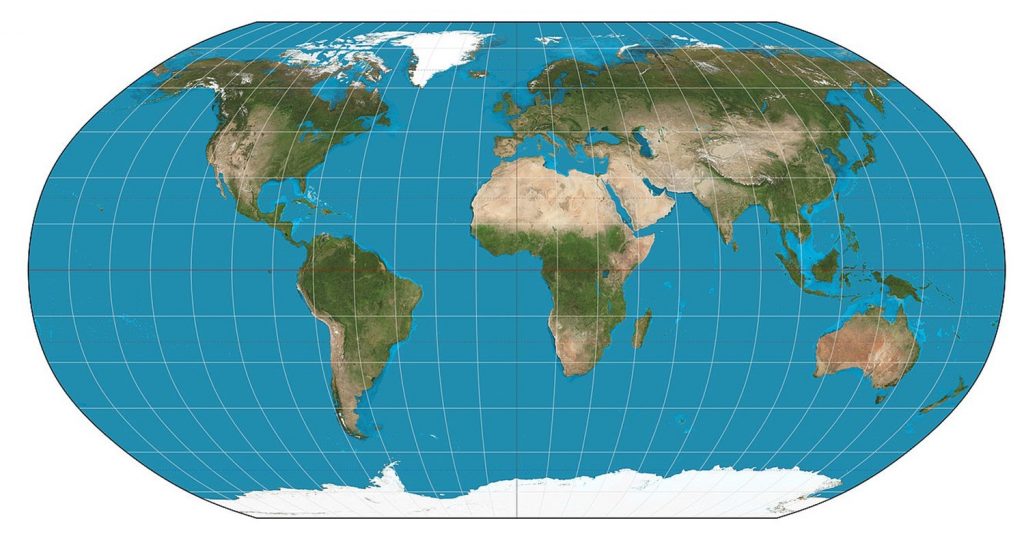
    Проекція Робінзона. Деякі проекції, включаючи проекцію Робінсона, дотримуються балансу між різними властивостями карти. Іншими словами, вони не зберігають форму, площу чи відстань, а натомість намагаються уникнути крайніх спотворень. [18]

    Компромісні проекції не зберігають нікого властивості, а натомість шукають компроміс, який мінімізує спотворення всіх видів, як при проекції Робінсона, яка часто використовується для дрібномасштабних тематичних карт світу.


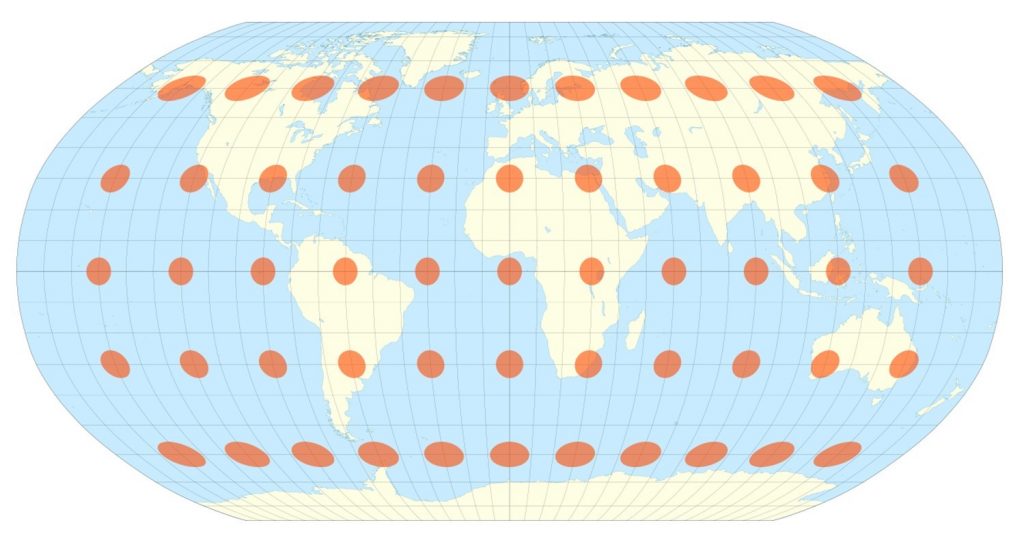
    Компромісне спотворення. Зверніть увагу, що деякі карти можуть не зберігати ні форму, ні площу, але роблять досить хорошу роботу в обох. [19]

    Інші прогнози мають справу з проблемою зробити 3D-глобус плоским шляхом розриву землі в стратегічних місцях. Перервані проекції, такі як перервана проекція Гомолозина Гуда, представляють землю в частках, зменшуючи кількість спотворень форми та площі біля полюсів. Проекція була розроблена в 1923 році Джоном Полом Гудом, щоб забезпечити альтернативу проекції Меркатора для зображення глобальних ареальних відносин.


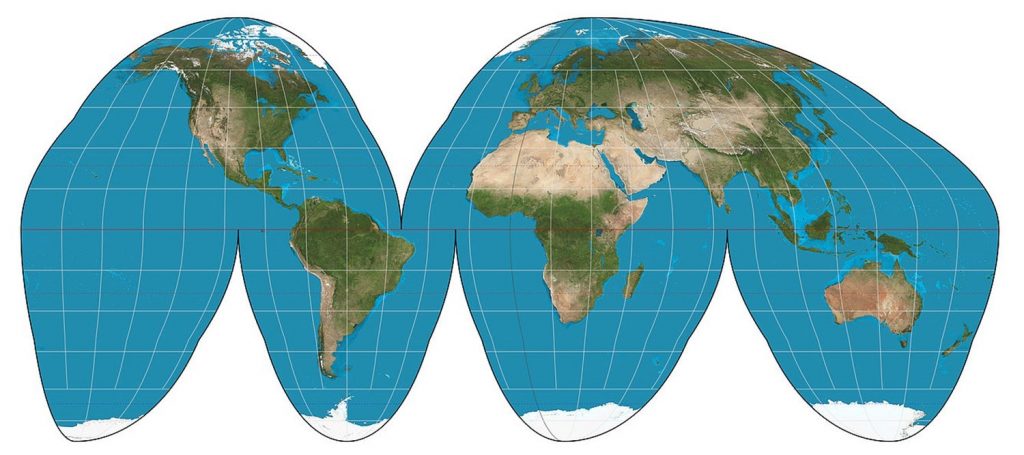
    Гомолозинова проекція Гуда світу. Ця рівноплотна проекція переривається в тому сенсі, що вона використовує частки або секції. [20]

    Перерваний Гомолозин Goode зберігає площу (так що вона рівна площа або еквівалент), але не зберігає форму (вона не є конформною).


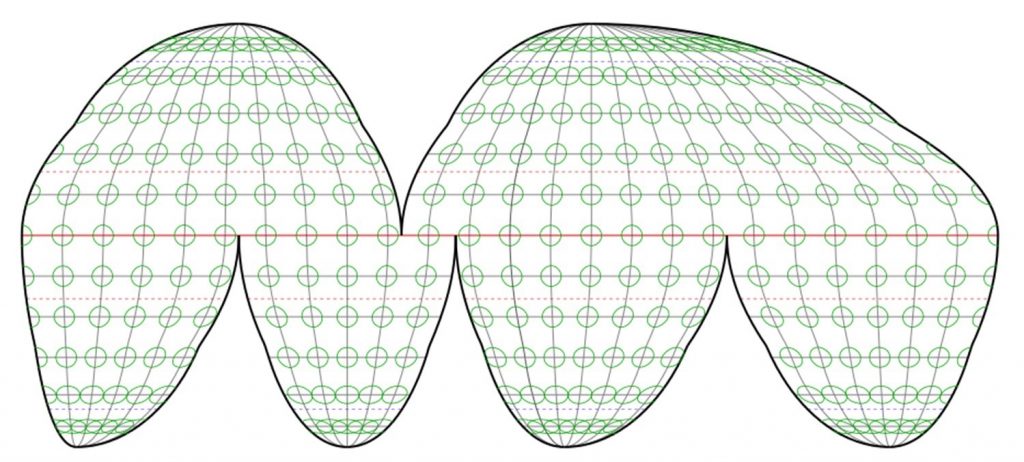
    Перерване спотворення. Ця проекція рівної площі зберігає площу, але спотворює форму, але не так сильно, як якби вона не була перервана. [21]

    Є також багато проекцій, які естетично приємні, але не призначені для навігації між місцями або для візуалізації даних. Приклади цих художніх проекцій включають проекцію Стабіуса-Вернера у формі серця.

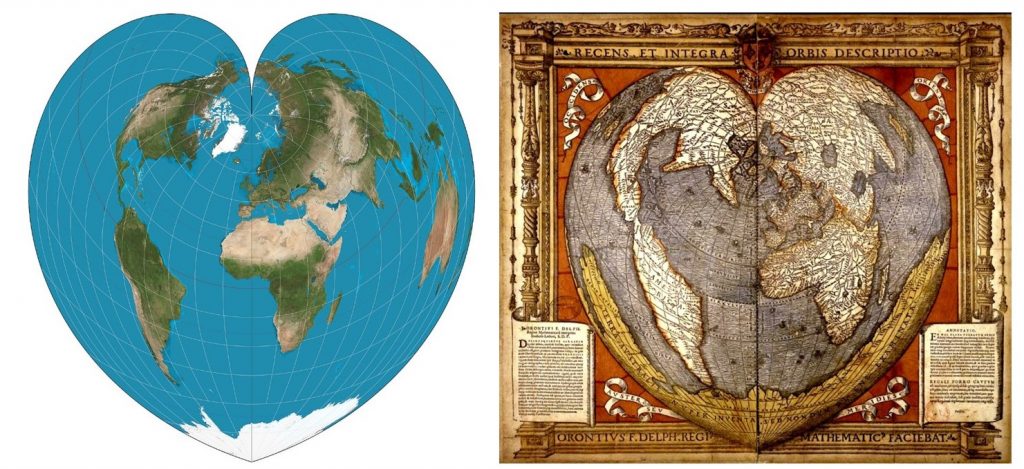
    Художні проекції. Багато проекцій цікаві та красиві, як ця проекція Стабіуса-Вернера, але не призначені для навігації між місцями або візуалізації даних. [22]

    3.5 Висновок

    У цьому розділі ми вивчили поняття масштабу, роздільної здатності та проекції. Є сотні проекцій, кожна з яких дещо по-іншому спотворює світ. Майте на увазі, що всі карти мають масштаб і є кілька важливих способів позначити цей масштаб. Усі карти також використовують проекцію, яка може бути сформована з поверхні, що розвивається, і може зберігати максимум одну або дві властивості.

    Ресурси

    • ГІС Вікісховище
    • Просторово інтегровані соціальні науки

    Посилання

    Частини розділу 3.1 адаптовані з Кемпбелл і Шін (2011). Основи геоінформаційних систем.

    Частини розділу 3.3 адаптовані з DiBiase (1998). Природа географічної інформації: відкритий геопросторовий підручник.

    1. КУБ.СМ ЗА 3,0. Адаптовано від Майкла Шмандта (nd). GIS Commons: Вступний підручник з геоінформаційних систем http://giscommons.org/output/ ⟩
    2. КУБ.СМ ПО-НК-СА 4.0. Адаптовано з Джей Кемпбелл і М.Шин (2012) https://2012books.lardbucket.org/boo...ics/index.html; На основі топографічних карт USGS (PD)
    3. КУБ.СМ ПО-НК-СА 4.0. Стівен Менсон 2017. Дані SocialExplorer та перепису населення США. ←
    4. КУБ.СМ ПО-НК-СА 4.0. Стівен Менсон 2017. Дані SocialExplorer та перепису населення США. ←
    5. КУБ.СМ ПО-НК-СА 3.0. Адаптовано з Dibiase et al. (2012) Картування нашого мінливого світу. https://www.e-education.psu.edu/geog160/node/1914. Географічний факультет Університету штату Пенсільванія. ←
    6. КУБ.СМ ПО-НК-СА 3.0. Адаптовано з Dibiase et al. (2012) Картування нашого мінливого світу. https://www.e-education.psu.edu/geog160/node/1914. Раешель Біанкетті, факультет географії, Університет штату Пенсільванія. ←
    7. CC ЗА НК-НД 3.0. Адаптовано з Dibiase et al. (2012) Картування нашого мінливого світу. https://www.e-education.psu.edu/geog160/node/1914. Географічний факультет Університету штату Пенсільванія. ←
    8. КУБ.СМ ПО-НК-СА 3.0. Адаптовано від Ентоні Робінсона. Карти та геопросторова революція, https://www.e-education.psu.edu/maps/l1_p5.html. Оригінальні фотографії Натан Белз ↑
    9. КУБ.СМ ПО-НК-СА 4.0. Стівен Менсон 2012. ←
    10. Ліцензія на вільну документацію GNU, версія 1.2. Адаптовано з Саттона, О.Дассау, М.Саттон (2009). Ніжне введення в ГІС. Головний директорат: Просторове планування та інформація, Департамент земельних справ, Східний Кап. http://docs.qgis.org/2.14/en/docs/ge...ucing_gis.html ㎡
    11. Публічне надбання. Національний атлас США національнийatlas.gov/статті/ма... заперечення.html㎡
    12. КУБ.СМ ЗА 3,0. Даніель Стреб https://commons.wikimedia.org/w/inde...curid=16115307
    13. Публічне надбання. https://commons.wikimedia.org/w/inde...p? курід=730484 ↑
    14. КУБ.СМ ЗА 3,0. Стефан Кун https://commons.wikimedia.org/w/index.php?curid=24628 ㎡
    15. КУБ.СМ ЗА 3,0. Даніель Стреб. https://commons.wikimedia.org/w/inde...curid=16115242 ㎡
    16. GFDL. Ерік Габа https://commons.wikimedia.org/w/inde...curid=12052919
    17. КУБ.СМ ЗА 3,0. Ерік Габа. https://commons.wikimedia.org/w/inde...curid=16115152. За Спіфф - На основі файлу:FLAG_of_the_United_Nations.svg, Суспільне надбання, commons.wikimedia.org/w/inde... curid=12835427⁰
    18. КУБ.СМ ЗА 3,0. Ерік Габа commons.wikimedia.org/w/inde... curid=16115337㎡
    19. GFDL. Дані Еріка Габа: Лінія світового узбережжя NGDC США (публічне надбання), GFDL, commons.wikimedia.org/w/індекс. phpcurid=4256 ⟩
    20. КУБ.СМ ЗА 3,0. Даніель Стреб. commons.wikimedia.org/w/inde... curid=16115269㎡
    21. КУБ.СМ ЗА 3,0. Даніель Стреб. commons.wikimedia.org/w/inde... curid=24727413㎡
    22. Даніель Стреб. commons.wikimedia.org/w/inde... curid=16115372. commons.wikimedia.org/w/w/inde... p? курід = 167921:05
    1. Back to top
    • Was this article helpful?

    Recommended articles

    1. Article type
      Chapter
      License
      CC BY-NC-SA
      Show Page TOC
      No on Page
    2. Tags
      1. authorname:smanson
      2. source[translate]-geo-5546