1.6: Класифікація

Хоча візуальної інтерпретації супутникового знімка може вистачити для деяких цілей, воно також має суттєві недоліки. Наприклад, якщо ви хочете дізнатися, де всі міські райони знаходяться на зображенні, а) навіть досвідченому аналітику зображень знадобиться багато часу, щоб переглянути все зображення і визначити, які пікселі є «міськими», а які ні, і б) отримана карта міських районів обов'язково буде дещо суб'єктивною. , оскільки він базується на інтерпретації індивідуального аналітика того, що означає «міський» і як це, ймовірно, з'явиться на зображенні. Дуже поширеною альтернативою є використання алгоритму класифікації для перекладу кольору, що спостерігається в кожному пікселі, у тематичний клас, який описує його домінантний покрив землі, перетворюючи таким чином зображення на карту земельного покриву. Цей процес називається класифікацією зображень.

Малюнок 1) Ву та ін., CC BY 3.0.

Можна виділити дві категорії підходів до класифікації зображень. Традиційний і найпростіший спосіб - подивитися на кожен піксель окремо і визначити, який тематичний клас відповідає його кольору. Зазвичай це називається класифікацією на піксель, і це те, що ми розглянемо спочатку. Новіший і все більш популярний метод - спочатку розділити зображення на однорідні сегменти, а потім визначити, який тематичний клас відповідає атрибутам кожного сегмента. Ці атрибути можуть бути кольором сегмента, а також іншими речами, такими як форма, розмір, текстура і розташування. Зазвичай це називається об'єктним аналізом зображень, і ми розглянемо це в другій половині цієї глави.

Навіть у категорії класифікації на піксель доступні два різних підходи. Один називається «контрольованою» класифікацією, оскільки аналітик зображень «контролює» класифікацію, надаючи деяку додаткову інформацію на ранніх стадіях. Інший називається «неконтрольованою» класифікацією, оскільки алгоритм виконує більшу частину роботи (майже) без сторонньої допомоги, а аналітик зображень повинен лише вступити в кінці і закінчити справу. Кожен має свої переваги і недоліки, які будуть викладені в наступному.

Контрольована класифікація на піксель

Ідея контрольованої класифікації полягає в тому, що аналітик зображень надає комп'ютеру деяку інформацію, яка дозволяє калібрувати алгоритм класифікації. Цей алгоритм потім застосовується до кожного пікселя зображення для отримання необхідної карти. Як це працює найкраще пояснити на прикладі. Зображення, показане на малюнку 44, з Каліфорнії, і ми хочемо перевести це зображення в класифікацію з наступними трьома (широкими) класами: «Міський», «Рослинність» та «Вода». Кількість класів та визначення кожного класу можуть мати великий вплив на успіх класифікації - у нашому прикладі ми ігноруємо той факт, що значні частини місцевості, здається, складаються з голого грунту (і тому насправді не потрапляють ні в один з наших трьох класів). І ми можемо зрозуміти, що вода на зображенні має дуже різний колір залежно від того, наскільки вона каламутна, і що деякі міські райони дуже світлі, а інші - темнішого відтінку сірого, але ми ігноруємо ці проблеми поки що.

Рисунок 44: Істинно-кольоровий композит, що показує частину зображення Landsat з Каліфорнії. Міська територія з деякою каламутною водою видно у верхньому правому куті, межує з сумішшю рослинних та безплідних районів та озером з чистою водою, а в нижній лівій частині зображення видно значною мірою лісиста гірська місцевість, з деякими яскравими очищеними ділянками поблизу центру ліворуч. Андерс Кнудбі, CC BY 4.0, на основі даних Landsat 5 (USGS).

«Нагляд» у контрольованій класифікації майже завжди приходить у вигляді набору даних калібрування, який складається з набору точок та/або полігонів, які, як відомо (або вважають) належать до кожного класу. На малюнку 45 такий набір даних надано у вигляді трьох багатокутників. Червоний багатокутник окреслює область, відому як «Urban», і аналогічно синій багатокутник - «Вода», а зелений багатокутник - «Рослинність». Зауважте, що приклад на рисунку 45 не є прикладом найкращої практики - бажано мати більше і менше багатокутників для кожного класу, розкинутих по всьому зображенню, оскільки це допомагає полігонам покривати лише пікселі призначеного класу, а також включати просторові варіації, наприклад. щільність рослинності, якість води тощо.

Малюнок 44, з накладенням трьох багатокутників. Червоний багатокутник являє собою область, відому аналітиком зображень як «Urban», синій багатокутник - «Вода», а зелений багатокутник - «Рослинність». Андерс Кнудбі, CC BY 4.0.

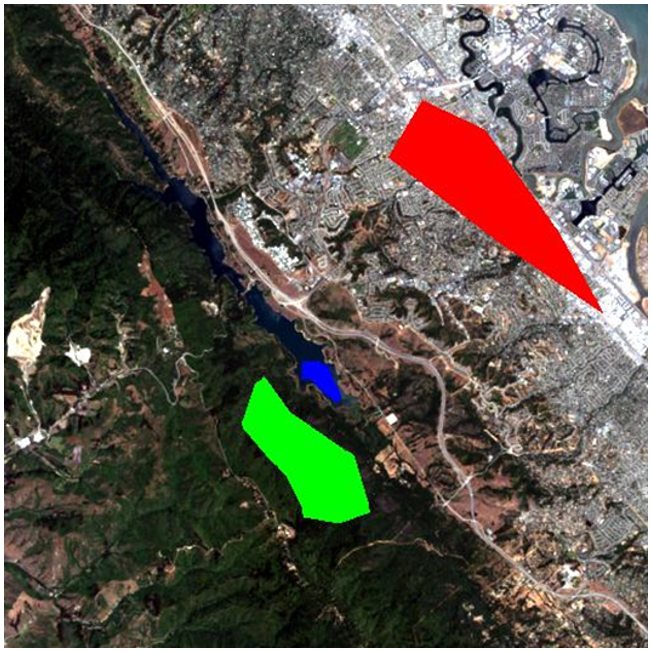
Тепер давайте розглянемо, як ці полігони допомагають нам перетворити зображення на карту трьох класів. По суті, багатокутники кажуть комп'ютеру «подивіться на пікселі під червоним багатокутником - ось як виглядають пікселі «Urban»», а потім комп'ютер може знайти всі інші пікселі на зображенні, які також виглядають так, і позначити їх «Urban». І так далі для інших класів. Однак деякі пікселі можуть виглядати трохи «міськими» і трохи схожими на «рослинність», тому нам потрібен математичний спосіб з'ясувати, який клас кожен піксель нагадує найбільше. Потрібен алгоритм класифікації.

Якщо взяти всі значення всіх пікселів в діапазонах Landsat 3 і 4 і показати їх на розсіювальному графіку, ми отримаємо щось на зразок рис. 46. Це зображення має 8-бітну радіометричну роздільну здатність, тому значення в кожній смузі теоретично варіюються від 0 до 255, хоча насправді ми бачимо, що найменші значення на зображенні більше 0. Значення з смуги 3 показані на осі x, а значення з смуги 4 на осі y.

Малюнок 44. Scatterplot створений за допомогою програмного забезпечення ENVI. Андерс Кнудбі, CC BY 4.0.

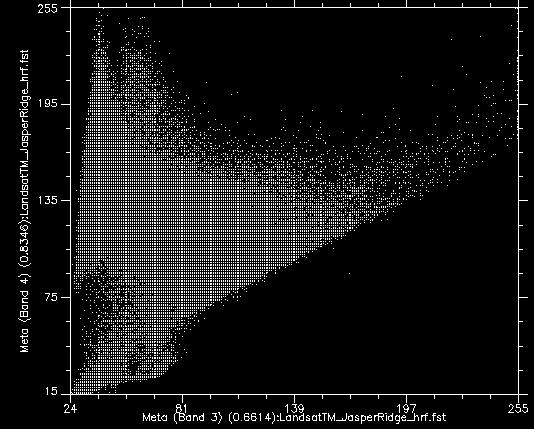
Тепер, якщо ми розфарбуємо всі точки, які походять від пікселів під червоним багатокутником (тобто пікселі, які ми «знаємо» як «міські»), і зробимо те ж саме з пікселями під синім і зеленим багатокутниками, ми отримаємо щось на зразок рис. 47. Є кілька важливих речей, які слід зазначити на малюнку 47. Всі сині точки («Вода») знаходяться в лівому нижньому кутку малюнка, нижче жовтого кола, з низькими значеннями в смузі 3 і низькими значеннями в смузі 4. Це дійсно характерно для води, оскільки вода дуже ефективно поглинає вхідне випромінювання в червоному (смуга 3) та ближньому інфрачервоному (смуга 4) довжині хвиль, тому дуже мало відбивається для виявлення датчиком. Зелені точки («Рослинність») утворюють довгу область уздовж лівої сторони фігури, з низькими значеннями в смузі 3 та помірними до високих значень у смузі 4. Знову ж таки, це здається розумним, оскільки рослинність ефективно поглинає вхідне випромінювання в червоній смузі (використовуючи його для фотосинтезу), відбиваючи вхідне випромінювання в ближньому інфрачервоному діапазоні. Червоні точки («Urban») утворюють більшу площу біля центру фігури і охоплюють набагато ширший діапазон значень, ніж будь-який з двох інших класів. Хоча їх значення аналогічні значенням «Рослинність» у смузі 4, вони, як правило, вищі в смузі 3.

Рисунок 46, але з кожною точкою, забарвленою багатокутником, під яким вона знаходиться. Scatterplot створений за допомогою програмного забезпечення ENVI. Андерс Кнудбі, CC BY 4.0.

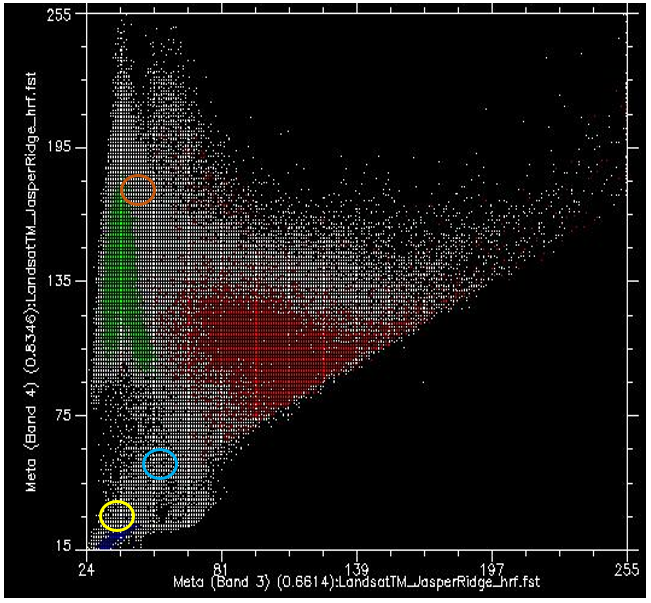
Те, що ми хочемо, щоб контрольований алгоритм класифікації зробив зараз, це взяти всі інші пікселі на зображенні (тобто всі білі точки на графіку розкиду) і призначити їх одному з трьох класів на основі їх кольору. Наприклад, якому класу, на вашу думку, слід призначити білі точки в жовтому колі на малюнку 47? Вода, напевно. А як щодо тих, хто в світло-коричневому колі? Рослинність, напевно. Але як щодо тих, хто в світло-блакитному колі? Не зовсім так просто визначити.

Примітка: Алгоритм класифікації може використовувати всі смуги зображення Landsat, а також будь-яку іншу інформацію, яку ми надаємо для всього зображення (наприклад, цифрова модель висоти), але оскільки найпростіше продовжувати показувати це у двох вимірах, використовуючи лише смуги 3 та 4, ми продовжуватимемо зроби так. Тільки майте на увазі, що графік розкиду насправді є n-мірним сюжетом, де n дорівнює кількості смуг (та інших шарів даних), які ми хочемо використовувати в класифікації.

Класифікатор мінімальної відстані

Один із способів оцінити, до якого класу належить кожен піксель, - це обчислити «відстань» між пікселем і центром усіх пікселів, які, як відомо, належать кожному класу, а потім призначити його найближчому. Під «відстанню» ми маємо на увазі відстань у «просторі ознак», в якому розміри визначаються кожною із змінних, які ми розглядаємо (у нашому випадку смуги 3 та 4), на відміну від фізичної відстані. Отже, наш простір особливостей є двовимірним, і відстані можна обчислити за допомогою стандартної евклідієвої відстані.

Як приклад, для точок на малюнку 48 ми розрахували середні значення всіх зелених, червоних і синіх пікселів для смуг 3 і 4 і позначили їх великими крапками. Припустимо, вони мають такі значення:

Таблиця 3: Середні значення в смугах 3 і 4 для класів «Міський», «Рослинність» і «Вода» показано на малюнку 49.

Середні значення	Червоні точки («Урбан»)	Зелені точки («Рослинність»)	Блакитні точки («Вода»)
Смуга 3	100	40	35
Група 4	105	135	20

Тоді припустимо, піксель, позначений жовтою крапкою на малюнку 48, має значення 55 в смузі 3 і 61 в смузі 4. Потім ми можемо обчислити евклідову відстань між точкою та середнім значенням кожного класу:

Відстань до червоного середнє: (100-55) 2+ (105-61) 2 = 62,9

Відстань до зеленого середнє: (40-55) 2+ (135-61) 2 = 75,5

Відстань до синього середнє: (35-55) 2+ (20-61) 2 = 45,6

Оскільки евклідова відстань найкоротша до центру синіх точок, класифікатор мінімальних відстаней присвоїть цю конкретну точку класу «Синій». Хоча класифікатор мінімальної відстані дуже простий і швидкий і часто працює добре, цей приклад ілюструє одну важливу слабкість: У нашому прикладі розподіл значень для класу «Вода» дуже малий - вода в основному завжди темна і синьо-зелена, і навіть каламутна вода або вода з великою кількістю водоростей в ньому в основному ще виглядає темно і синьо-зелено. Розподіл значень для класу «Рослинність» набагато більший, особливо в смузі 4, оскільки деяка рослинність густа, а деяка ні, деяка рослинність здорова, а деякі ні, деяка рослинність може бути змішана з темним грунтом, яскравим грунтом або навіть деякими міськими особливостями, такими як дорога. Те ж саме стосується класу «Urban», який має широкий розподіл значень як в діапазонах 3, так і 4. Насправді жовта точка на малюнку 48, швидше за все, не є водою, тому що вода, яка має такі високі значення в обох діапазонах 3 і 4, в основному не існує. Набагато частіше буде незвичайний вид рослинності, або незвичайна міська територія, або (ще більш імовірно) суміш між цими двома класами. Наступний класифікатор, який ми розглянемо явно, враховує розподіл значень у кожному класі, щоб усунути цю проблему.

48: Класифікатор мінімальної відстані призначає клас, центр якого є найближчим (у просторі об'єктів) до кожного пікселя. Середнє значення всіх червоних точок, в смугах 3 і 4, позначається великою червоною крапкою, і аналогічно для зеленої і синьої точок. Жовта крапка вказує на піксель, який ми хочемо призначити одному з трьох класів. Scatterplot створений за допомогою програмного забезпечення ENVI. Андерс Кнудбі, CC BY 4.0.

Класифікатор максимальної правдоподібності

Ще близько 10 років тому класифікатор максимальної ймовірності був алгоритмом класифікації зображень, і він все ще популярний, реалізований у всіх серйозних програмних забезпеченнях дистанційного зондування і, як правило, серед найбільш ефективних алгоритмів для даного завдання. Математичні описи того, як це працює, можуть здатися складними, оскільки вони покладаються на байєсівську статистику, застосовану в декількох вимірах, але принцип відносно простий: замість того, щоб обчислювати відстань до центру кожного класу (у просторі ознак) і таким чином знайти найближчий клас, ми обчислимо ймовірність того, що піксель належить кожному класу, і таким чином знайти найбільш ймовірний клас. Що нам потрібно зробити, щоб математика працювала, - це зробити кілька припущень.

• Будемо вважати, що перш ніж ми дізнаємося колір пікселя, ймовірність його належності до одного класу така ж, як і ймовірність його належності до будь-якого іншого класу. Це здається досить розумним (хоча на нашому зображенні явно набагато більше «рослинності», ніж «Вода», тому можна стверджувати, що піксель з невідомим кольором, швидше за все, є рослинністю, ніж водою... це може бути включено до класифікатора, але рідко є, і ми будемо ігнорувати його поки що)
• Будемо вважати, що розподіл значень в кожній смузі і для кожного класу є гаусовим, тобто слід за нормальним розподілом (кривою дзвінка).

Для початку з одновимірного прикладу наша ситуація могла б виглядати так, якби у нас було всього два класи:

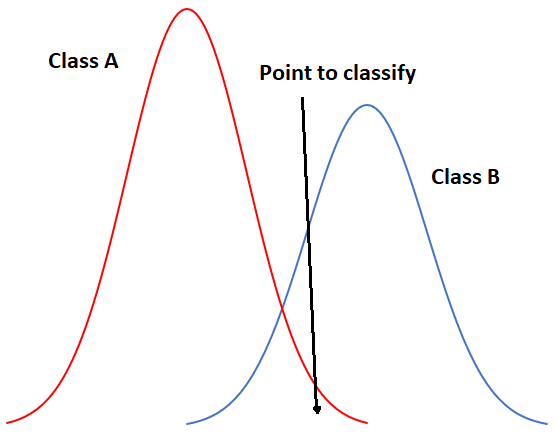
49: Одновимірний приклад класифікації максимальної правдоподібності з двома класами. Андерс Кнудбі, CC BY 4.0.

На малюнку 49 вісь x представляє значення в смузі зображення, а вісь y показує кількість пікселів у кожному класі, який має задане значення в цій смузі. Зрозуміло, що клас A зазвичай має низькі значення, а клас B зазвичай має високі значення, але розподіл значень у кожній смузі досить значний, щоб між ними було певне перекриття. Оскільки обидва розподілу є гаусовими, ми можемо обчислити як середнє, так і стандартне відхилення для кожного класу, а потім ми можемо обчислити z-бал (скільки стандартних відхилень ми далеко від середнього). На малюнку 49 два класи мають однакове стандартне відхилення («дзвони» мають однакову «ширину»), і оскільки точка розташована трохи ближче до середнього класу B, ніж до класу A, її Z-оцінка була б найнижчою для класу B, і вона буде присвоєна цьому класу. Трохи більш реалістичний приклад наведено нижче на малюнку 50, де ми маємо два виміри і три класи. Стандартні відхилення в смузі 4 (вісь x) та смузі 3 (вісь y) показані як контури рівноймовірності. Завдання класифікатора максимальної правдоподібності в даному випадку полягає в тому, щоб знайти клас, для якого точка лежить в межах контуру рівності, найближчого до центру класу. Дивіться, наприклад, що контури для класу A та класу B перекриваються, і що стандартні відхилення класу A більші, ніж у класі B. В результаті червона крапка знаходиться ближче (у просторі об'єктів) до центру класу B, ніж до центру класу A, але вона знаходиться на третьому контурі рівноймовірності Клас B та другий клас A Класифікатор мінімальної відстані класифікував би цю точку як «клас B» на основі коротшої евклідівської відстані, тоді як класифікатор максимальної ймовірності класифікував би її як «клас A» через більшу ймовірність належності до цього класу (відповідно до припущень зайнятих). Що, швидше за все, буде правильним? Більшість порівнянь між цими класифікаторами припускають, що класифікатор максимальної ймовірності, як правило, дає більш точні результати, але це не є гарантією того, що він завжди перевершує.

50: Двовимірний приклад ситуації класифікації максимальної ймовірності, з шістьма класами, які мають нерівні стандартні розподіли. Андерс Кнудбі, CC BY 4.0.

Непараметричні класифікатори

Протягом останнього десятиліття вчені дистанційного зондування все частіше зверталися до галузі машинного навчання, щоб прийняти нові методи класифікації. Ідея класифікації принципово дуже загальна - у вас є деякі дані про щось (у нашому випадку значення в діапазонах для пікселя) і ви хочете дізнатися, що це таке (в нашому випадку, що таке земний покрив). Проблема навряд чи може бути більш загальною, тому її версії зустрічаються скрізь: Банк має деяку інформацію про клієнта (вік, стать, адреса, дохід, історія погашення кредиту) і хоче з'ясувати, чи слід його вважати «низьким ризиком», «середнім ризиком» або «високим ризиком» для нового кредиту в розмірі 100 000 доларів. Метеоролог має інформацію про поточну погоду («дощова, 5°C») та атмосферні змінні («1003 мб, 10 м/с вітер з північного заходу»), і повинен визначити, чи буде дощ чи ні через три години. Комп'ютер має деяку інформацію про відбитки пальців, знайдені на місці злочину (довжина, кривизна, відносне положення, кожного рядка) і повинен з'ясувати, чи є вони вашими або чужими). Оскільки завдання є загальним, і оскільки користувачі за межами сфери дистанційного зондування мають величезні суми грошей і можуть використовувати алгоритми класифікації для отримання прибутку, вчені з комп'ютерів розробили багато методів для вирішення цього загального завдання, і деякі з цих методів були прийняті в дистанційному зондуванні. Ми розглянемо один приклад тут, але майте на увазі, що існує багато інших загальних алгоритмів класифікації, які можна використовувати в дистанційному зондуванні.

Той, який ми розглянемо, називається класифікатором дерева рішень. Як і в інших класифікаторах, класифікатор дерева рішень працює у двоетапному процесі: 1) Калібруйте алгоритм класифікації та 2) застосуйте його до всіх пікселів зображення. Класифікатор дерева рішень калібрується шляхом рекурсивного поділу всього набору даних (всі пікселі під полігонами на рис. 45), щоб максимізувати однорідність двох частин (званих вузлами). Невелика ілюстрація: скажімо, у нас є 7 точок даних (ви ніколи не повинні мати лише сім точок даних при калібруванні класифікатора, це невелике число використовується лише для ілюстрації!) :

Таблиця 4: Сім точок даних, які використовуються для розробки класифікатора дерева рішень.

Точка даних	Значення діапазону 1	Значення смуги 2	Актуальний клас
1	10	30	A
2	20	40	A
3	30	40	A
4	15	55	Б
5	35	40	Б
6	40	35	Б
7	45	35	Б

Перше завдання полягає в тому, щоб знайти значення, або в смузі 1, або в смузі 2, яке може бути використано для поділу набору даних на два вузли таким чином, щоб, наскільки це можливо, всі точки класу A знаходяться в одному вузлі, а всі точки класу B знаходяться в іншому. Алгоритмічно це робиться шляхом тестування всіх можливих значень і кількісної оцінки однорідності результуючих класів. Отже, ми бачимо, що найменше значення в Band 1 дорівнює 10, а найбільше - 45. Якщо ми розділимо набір даних відповідно до правила, що «Усі точки з діапазоном 1 < 11 переходять до вузла X, а всі інші - до вузла Y», ми закінчимо розділеними точками так:

51: Пункти розділені відповідно до порогового значення 11 в смузі 1. Андерс Кнудбі, CC BY 4.0.

Як ми бачимо, це залишає нам одну точку «A» в одному вузлі (X), а дві точки «A» та чотири точки «B» в іншому вузлі (Y). Щоб з'ясувати, чи можемо ми зробити краще, ми намагаємося використовувати значення 12 замість 11 (що дає нам той самий результат), 13 (все одно те ж саме), і так далі, і коли ми перевірили всі значення в смузі 1, ми продовжуємо йти з усіма значеннями в смузі 2. Зрештою, ми виявимо, що використання значення 31 в діапазоні 1 дає нам наступний результат:

52: Точки плюються відповідно до порогового значення 31 в смузі 1. Андерс Кнудбі, CC BY 4.0.

Це майже ідеально, за винятком того, що у нас є один «B» у вузлі X. Але добре, досить добре для першого розколу. Ми можемо зобразити це у вигляді «дерева» так:

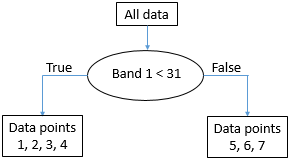
53: Виникаюча «деревоподібна» структура з розбиття даних на порогове значення 31 в смузі 1. Кожна колекція точок даних називається вузлом. «Кореневий вузол» містить усі точки даних. «Листові вузли» також називають «кінцевими вузлами», вони є кінцевими точками. Андерс Кнудбі, CC BY 4.0.

Вузол з точками даних 5, 6 і 7 (всі мають значення діапазону 1 вище 31) тепер називається «чистим вузлом» - він складається з точок даних лише одного класу, тому нам більше не потрібно розділяти його. Вузли, які є кінцевими точками, також називаються «листям». Вузол з точками даних 1, 2, 3 і 4 не є «чистим», оскільки містить суміш точок класу A та класу B. Таким чином, ми йдемо через знову і перевірити всі різні можливі значення, які ми можемо використовувати як поріг, щоб розділити цей вузол (і тільки цей вузол), в обох діапазонах. Буває так, що точка з класу B в цьому вузлі має значення в смузі 2, що вище, ніж всі інші точки, тому розділене значення 45 працює добре, і ми можемо оновити дерево так:

54: Остаточна структура «дерева». Усі вузли (кінцеві частини набору даних) тепер чисті. Андерс Кнудбі, CC BY 4.0.

Маючи «дерево» на місці, тепер ми можемо взяти кожен інший піксель зображення і «скинути його вниз» по дереву, щоб побачити, на якому листі воно приземляється. Наприклад, піксель зі значеннями 35 у смузі 1 та 25 у смузі два «піде праворуч» під час першого тесту і, таким чином, приземлиться на аркуші, який містить точки даних 5, 6 та 7. Оскільки всі ці точки були з класу B, цей піксель буде класифікуватися як клас B і так далі.

Зверніть увагу, що листки не повинні бути «чистими», деякі дерева припиняють розщеплювати вузли, коли вони менші за певний розмір, або використовують якийсь інший критерій. У такому випадку піксельній посадці в такому листі буде присвоєно клас, який має найбільше точок у цьому листі (а інформація про те, що це не був чистий лист, може навіть використовуватися для вказівки на те, що класифікація цього конкретного пікселя піддається деякій невизначеності).

Класифікатор дерева рішень є лише одним із багатьох можливих прикладів непараметричних класифікаторів. Він рідко використовується безпосередньо у формі, наведеній вище, але є основою для деяких найбільш успішних алгоритмів класифікації, що використовуються сьогодні. Інші популярні алгоритми непараметричної класифікації включають нейронні мережі та підтримують векторні машини, обидва з яких реалізовані в багатьох програмних забезпеченнях дистанційного зондування.

Неконтрольована класифікація на піксель

Що робити, якщо у нас немає даних, необхідних для калібрування алгоритму класифікації? Якщо у нас немає полігонів, показаних на малюнку 45, або точок даних, показаних у таблиці 4? Що ми тоді робимо? Натомість ми використовуємо неконтрольовану класифікацію!

Неконтрольована класифікація триває, дозволяючи алгоритму розділити пікселі зображення на «природні кластери» - комбінації значень смуг, які зазвичай зустрічаються на зображенні. Після ідентифікації цих природних кластерів аналітик зображень може позначати їх, як правило, на основі візуального аналізу того, де ці кластери знаходяться на зображенні. Кластеризація значною мірою автоматична, хоча аналітик надає кілька початкових параметрів. Одним з найпоширеніших алгоритмів, що використовуються для пошуку природних кластерів на зображенні, є алгоритм K-Means, який працює так:

1) Аналітик визначає потрібну кількість класів. В основному, якщо ви хочете карту з високою тематичною деталізацією, ви можете встановити велику кількість занять. Зверніть увагу також, що класи можуть бути об'єднані пізніше, тому часто є гарною ідеєю встановити кількість бажаних класів трохи вище, ніж те, що ви думаєте, що ви хочете в кінці. Кількість «насіннєвих» точок, що дорівнює бажаній кількості класів, потім випадковим чином розміщуються в просторі функцій.

55: K-означає крок класифікації 1. Ряд «насіннєвих» точок (кольорових крапок) випадковим чином розподіляються в просторі об'єктів. Сірі точки тут представляють пікселі, які потрібно кластерувати. Змінено з K означає приклад кроку 1 від Weston.pace, Wikimedia Commons, CC BY-SA 3.0.

2) Потім кластери генеруються навколо «насіннєвих» точок шляхом виділення всіх інших точок до найближчого насіння.

56: Навколо кожного насіння утворюється скупчення шляхом виділення всіх точок до найближчого насіння. Змінено з K означає приклад кроку 2 від Weston.pace, Wikimedia Commons, CC BY-SA 3.0.

3) Центроїд (географічний центр) точок в кожному кластері стає новим «насінням».

57: Насіння переміщують в центроїд кожного скупчення. Центроїд обчислюється як географічний центр кожного кластера, тобто він стає розташованим на середньому значенні x всіх точок кластера та середнім значенням y всіх точок кластера. Змінено з K означає приклад кроку 3 від Weston.pace, Wikimedia Commons, CC BY-SA 3.0.

4) Повторіть кроки 2 і 3 до зупинки критерію. Критерієм зупинки може бути те, що жодна точка не рухається до іншого кластера, або що центроїд кожного кластера рухається менше, ніж заздалегідь задана відстань, або що певна кількість ітерацій було завершено.

Інші алгоритми класифікації без нагляду роблять кластеризацію трохи інакше. Наприклад, популярний алгоритм під назвою ISODATA також дозволяє розділяти великі кластери під час процесу кластеризації, і аналогічно для об'єднання невеликих сусідніх кластерів. Тим не менш, результатом алгоритму кластеризації є те, що кожен піксель у всьому зображенні є частиною кластера. Отже, надія полягає в тому, що кожен кластер представляє тип земного покриву, який може бути ідентифікований аналітиком зображень, наприклад, наклавши розташування всіх пікселів кластера на вихідне зображення, щоб візуально визначити, чому відповідає цей кластер. Це завершальний етап неконтрольованої класифікації — маркування кожного з кластерів, які були вироблені. Це крок, на якому може бути зручно об'єднати кластери, якщо, наприклад, у вас є одне скупчення, яке відповідає каламутній воді, а інше - чистої води. Якщо ви спеціально не зацікавлені в якості води, диференціація цих двох, ймовірно, не важлива, і об'єднання їх забезпечить більш чіткий картографічний продукт. Крім того, у вас може бути просто два скупчення, які, здається, відповідають здоровому листяному лісу. Навіть якщо ви працюєте на лісову службу, якщо не зможете впевнено розібратися, в чому різниця між цими двома скупченнями, можна об'єднати їх в одне і назвати «листяним лісом».

Як приклад, на зображенні нижче показано вихідне зображення у фоновому режимі, а центральні пікселі пофарбовані відповідно до продукту класифікації без нагляду. Зрозуміло, що «синя» область відповідає пікселям, покритим водою, а зелена зона багато в чому відповідає рослинності. Більш детальний аналіз зображення буде необхідним для відповідного позначення кожної області, особливо червоної та сірої.

58: Приклад відповідності між оригінальним зображенням і кластерами, сформованими в процесі класифікації без нагляду. Андерс Кнудбі, CC BY 4.0.

Класифікація земного покриву є одним із найстаріших застосувань дистанційного зондування, і це те, що багато національних урядів регулярно роблять для своєї території. Наприклад, в Канаді Центр дистанційного зондування Канади співпрацює з партнерами з США та Мексики над створенням північноамериканської карти земельного покриву. Глобальні карти земельного покриву також виробляються різними установами, такими як USGS, Мерілендський університет, ESA та Китай, щоб назвати лише деякі з них.

Одним з типових недоліків схем класифікації зображень, які працюють на рівні пікселів за пікселем, є те, що зображення галасливі, а карти земного покриву, зроблені із зображень, успадковують цей шум. Ще одним більш важливим недоліком є те, що в зображенні є інформація, що виходить за межі того, що міститься в окремих пікселів. Зображення є ідеальною ілюстрацією приказки про те, що «ціле більше суми його частин», оскільки зображення мають структуру, а структура не враховується при погляді на кожен піксель незалежно від контексту, що надається всіма сусідніми пікселями. Наприклад, навіть не знаючи кольору пікселя, якщо я знаю, що всі його сусідні пікселі класифікуються як «вода», я можу з великою впевненістю сказати, що піксель, про який йде мова, також є «водою». Я буду помилятися іноді, але правильно більшу частину часу. Тепер ми розглянемо метод, який називається об'єктним аналізом зображень, який враховує контекст при створенні класифікацій зображень. Ця перевага часто дозволяє йому перевершити більш традиційні методи класифікації пікселів за пікселями.

Об'єктний аналіз зображень (OBIA)

Багато нових досягнень у світі дистанційного зондування походять з апаратної сторони речей. Запускається новий датчик, і він має кращу просторову або спектральну роздільну здатність, ніж попередні датчики, або він виробляє менш галасливі зображення, або він робиться у вільному доступі, коли альтернативи коштували. Безпілотники - ще один приклад: вид знімків, які вони виробляють, істотно не відрізняється від того, що раніше було доступно з камер на пілотованих літаках - насправді він часто поступається за якістю - але низька вартість дронів та легкість, з якою вони можуть бути розгорнуті неекспертами, створили революцію за обсягом доступних знімків з малих висот, і вартості отримання знімків високої роздільної здатності для невеликої ділянки.

Одним з небагатьох суттєвих досягнень, які прийшли з програмної сторони, є розробка об'єктного аналізу зображень (OBIA). Основним принципом OBIA є розглядати зображення, яке складається з об'єктів, а не пікселів. Однією з переваг цього є те, що люди, як правило, бачать світ як складений з об'єктів, а не пікселів, тому аналіз зображень, який приймає той самий погляд, дає результати, які легше інтерпретуються людьми. Наприклад, коли ви дивитеся на рис. 59, ви напевно бачите обличчя чоловіка, (якщо ви його знаєте, ви також дізнаєтеся, хто такий чоловік).

59: Роберт Де Ніро. Або, якщо ви програмне забезпечення для аналізу зображень на основі пікселів, трисмуговий растр з 1556 стовпцями та 2247 рядками, кожен піксель і смуга відображають різний рівень яскравості. Портрет Роберта Де Ніро КВІФФ Петра Новака (che), Wikimedia Commons, CC BY-SA 2.5.

Оскільки це цифрове зображення, ми знаємо, що воно насправді складається з декількох пікселів, чітко розташованих у стовпцях і рядках, і що яскравість (тобто інтенсивність червоного, зеленого та синього кольорів у кожному пікселі) може бути представлена трьома числами. Таким чином, ми могли б класифікувати яскраві частини зображення як «шкіру», а менш яскраві частини - як «інші», змішаний клас, що включає очі, волосся, тіні та фон. Це не особливо корисна або значуща класифікація, хоча! Що було б більш значущим, було б класифікувати зображення на класи типу «око», «рука», «волосся», «ніс» і т.д.

Приклад, дещо більш актуальний для дистанційного зондування, наведено нижче на малюнку 60, на якому міську територію класифікували на об'єкти, включаючи легко впізнаваний стадіон, вулиці, окремі будівлі, рослинність тощо.

60: Класифікація міської території за допомогою об'єктного аналізу зображень. Об'єктний аналіз зображень від Уддинкабіра, Wikimedia Commons, CC BY-SA 4.0.

Сегментація зображень

Мета сегментації зображення — взяти всі пікселі зображення та розділити їх на сегменти — суміжні частини зображення, які мають схожий колір. Сегментація зображень корисна, оскільки вона відводить нас від аналізу зображення за пікселем і натомість дозволяє аналізувати окремі сегменти. У цьому є пара дуже важливих переваг. Перш за все, ми можемо подивитися на «середній колір» сегмента і використовувати його для класифікації цього сегмента, а не використовувати колір кожного окремого пікселя для класифікації цього пікселя. Якщо ми маємо справу з галасливими образами (а ми завжди є!) , використання середніх сегментів зменшує вплив шуму на класифікацію. По-друге, сегменти мають ряд атрибутів, які можуть бути значущими і можуть бути використані для їх класифікації — атрибути пікселів не мають. Наприклад, сегмент зображення складається з декількох пікселів, і, таким чином, ми можемо кількісно оцінити його розмір. Оскільки не всі сегменти матимуть однаковий розмір, у атрибуті «розмір сегмента» міститься інформація, яка може бути використана для класифікації сегментів. Наприклад, на малюнку 60 зверніть увагу, що сегмент, що покриває озеро, досить великий порівняно з усіма сегментами на суші. Це тому, що озеро є дуже однорідною частиною зображення. Така ж різниця спостерігається між різними частинами суші - сегменти на захід від озера, як правило, більші, ніж ті, що на південний захід від озера, знову ж таки, це тому, що вони більш однорідні, і ця однорідність може сказати нам щось важливе про те, який земний покрив там знаходиться. Крім розміру, сегменти мають велику кількість інших атрибутів, які можуть бути корисними або не можуть бути корисними при класифікації. Кожен сегмент має певну кількість сусідніх сегментів, і кожен сегмент також темніший або світліший або десь посередині порівняно з сусідами. На цій сторінці наведено список атрибутів, які ви можете обчислити для сегментів у модулі видобутку функцій ENVI (який на сьогоднішній день не є найповнішим таким модулем). Можливість отримати всю цю інформацію про сегменти може допомогти класифікувати їх, і ця інформація не доступна для пікселів (наприклад, всі пікселі мають рівно чотири сусіди, якщо вони не розташовані на краю зображення, тому кількість сусідів не є корисною для класифікації пікселя).

Існують різні види алгоритмів сегментації, і всі вони обчислювально-складні. Деякі з них є відкритим вихідним кодом, а інші є власними, тому ми навіть не знаємо, як вони працюють. Тому ми не будемо вдаватися в деталі з специфікою алгоритмів сегментації, але вони мають кілька спільних речей, які ми можемо розглянути.

• Масштаб: Усі алгоритми сегментації потребують «масштабного коефіцієнта», який користувач встановлює, щоб визначити, наскільки великими він хоче мати результуючі сегменти. Масштабний коефіцієнт не обов'язково дорівнює певній кількості пікселів або певній кількості сегментів, але зазвичай вважається відносним числом. Те, що це насправді означає з точки зору розміру на місцях результуючих сегментів, зазвичай виявляється шляхом проб і помилок.
• Колір проти форми: Усі алгоритми сегментації повинні робити вибір щодо того, де малювати межі кожного сегмента. Оскільки зазвичай бажано мати сегменти, які не надто дивної форми, це часто передбачає компроміс між тим, чи додавати піксель у існуючий сегмент, якщо а) цей піксель робить колір сегмента більш однорідним, але також призводить до більш дивної форми, або б) якщо цей піксель робить колір сегмент менш однорідний, але призводить до більш компактної форми. Один або кілька параметрів зазвичай контролюють цей компроміс, а що стосується параметра «масштаб», пошук найкращого параметра є питанням проб і помилок.

В ідеальному світі сегментація зображення створювала б сегменти, кожен з яких відповідає одному, а саме одному об'єкту реального світу. Наприклад, якщо у вас є зображення міської місцевості і ви хочете скласти карту всіх будівель, крок сегментації зображення в ідеалі призведе до того, що кожна будівля буде власним сегментом. На практиці це, як правило, неможливо, оскільки алгоритм сегментації не знає, що ви шукаєте будівлі... якщо ви шукали карту черепиці, наявність сегментів, що відповідають цілому даху, було б марно, як це було б, якби ви шукали карту міських кварталів. «Але я міг би встановити коефіцієнт масштабу відповідно», - скажете ви, і це певною мірою вірно. Але не всі дахи однакового розміру! Якщо ви відображаєте будівлі на зображенні, яке містить як ваш власний будинок, так і Пентагон, ви навряд чи знайдете масштабний коефіцієнт, який дає вам рівно один сегмент, що охоплює кожну будівлю... Рішенням цієї проблеми є, як правило, деяке ручне втручання, в якому сегменти виробляються початковим сегментація модифікується за конкретними правилами. Наприклад, ви можете вибрати масштабний коефіцієнт, який працює для вашого будинку, і залишити Пентагон розділеним на 1000 сегментів, а потім об'єднати всі сусідні сегменти, які мають дуже схожі кольори. Якщо припустити, що дах Пентагону досить однорідний, що об'єднає всі ці сегменти, і якщо припустити, що ваш власний будинок оточений чимось іншим виглядом, наприклад, вулицею, заднім двором чи під'їзною дорогою, ваш власний дах не буде зливатися з сусідніми сегментами. Ця здатність вручну возитися з процесом для досягнення бажаних результатів є одночасно великою силою і важливою слабкістю об'єктного аналізу зображень. Це сила, оскільки дозволяє аналітику зображень отримувати надзвичайно точні результати, але слабкість, оскільки навіть експерти-аналітики вимагають багато часу, щоб зробити це для кожного зображення. Приклад хорошої сегментації показаний на малюнку 61, який також ілюструє вплив змін параметрів сегментації (порівняйте нижнє ліве і нижнє праве зображення).

Тут варто зазначити, що об'єктний аналіз зображень спочатку був розроблений і широко використовувався в галузі медичної візуалізації, для аналізу рентгенівських знімків, клітин, помічених під мікроскопами тощо. Дві речі досить різні між медичною візуалізацією та дистанційним зондуванням: У медичній візуалізації на здоров'я людей дуже безпосередньо впливає аналіз зображення, тому той факт, що для отримання точного результату потрібен додатковий час, є меншим обмеженням, ніж у дистанційному зондуванні, де людський вплив бідних аналіз зображень дуже важко оцінити (хоча в кінцевому підсумку вони можуть бути настільки ж важливими). Інша проблема полягає в тому, що зображення, вивчені лікарями, створюються у високо контрольованих налаштуваннях, практично без фонового шуму, ціль зображення завжди у фокусі, і їх можна переробити, якщо їх важко проаналізувати. У дистанційному зондуванні, якщо серпанок, погана освітленість, дим або інші фактори навколишнього середовища поєднуються для створення галасливого зображення, наш єдиний варіант - почекати до наступного разу, коли супутник знову пройде над територією.

Малюнок 6) Чень та ін., CC BY 4.0.

Класифікація сегментів

Класифікація сегментів теоретично може слідувати підходам із наглядом та без нагляду, викладеним у розділі про класифікацію на піксель. Тобто ділянки з відомим земним покривом можуть бути використані для калібрування класифікатора на основі заздалегідь визначеного набору атрибутів сегментів (контрольований підхід), або набір заздалегідь визначених атрибутів може бути використаний в алгоритмі кластеризації для визначення природних кластерів сегментів на зображенні, які потім можуть бути позначені іміджевий аналітик (неконтрольований підхід). Однак на практиці об'єктний аналіз зображень часто протікає більш інтерактивним способом. Один із поширених підходів полягає в тому, що аналітик розробляє набір правил, який структурований як дерево рішень, бачить, який результат, який набір правил виробляє, модифікує або додає до нього, і перевіряє знову, все це в дуже інтенсивному ітераційному процесі. Це одна з тих областей, де дистанційне зондування здається більше мистецтвом, ніж наукою, тому що аналітики зображень отримують досвід роботи з цим процесом і стають кращими та кращими в ньому, в основному розробляючи власний «стиль» розробки наборів правил, необхідних для досягнення гарної класифікації. Наприклад, після сегментації зображення ви можете відокремити рукотворні поверхні (дороги, тротуари, автостоянки, дахи) від природної поверхні, що, як правило, тому що перші мають тенденцію бути сірими, а другі, як правило, не є. Таким чином, ви розробляєте змінну, яка кількісно визначає, наскільки сірий сегмент (наприклад, використовуючи значення «насиченості» ВПГ, докладніше тут), і вручну знаходите порогове значення, яке ефективно відокремлює природні від техногенних поверхонь у вашому зображенні. Якщо ви займаєтеся урбаністичними дослідженнями, ви можете також розрізняти різні види рукотворних поверхонь. Всі вони сірі, тому з класифікатором на основі пікселів вам тепер не пощастило. Однак ви маєте справу з сегментами, а не пікселями, тому ви кількісно оцінюєте, наскільки витягнутий кожен сегмент, і визначаєте порогове значення, яке дозволяє відокремлювати дороги та тротуари від дахів та парковок. Потім ви використовуєте ширину витягнутих сегментів, щоб відрізнити дороги від тротуарів, і, нарешті, ви використовуєте той факт, що парковки мають сусідні сегменти, які є дорогами, а дахи - ні, щоб розділити ці два. Пошук усіх правильних змінних для використання (значення насичення HSV, подовження, ширина, клас сусіднього сегмента) - це за своєю суттю суб'єктивна вправа, яка включає випробування та помилки, і що ви отримуєте краще з досвідом. І як тільки ви створили перше дерево рішень (або подібну) структуру для вашого набору правил, дуже ймовірно, що ваші очі будуть звернені до одного або двох сегментів, які, незважаючи на ваші зусилля, все ще були неправильно класифіковані (можливо, є випадковий дах, який простягається так далеко над будинком, що його сусідні сегмент дійсно дорога, тому його неправильно класифікували як стоянку). Тепер ви можете пройти і створити додатково складні правила, які вирішують ці конкретні проблеми, у процесі, який закінчується лише тоді, коли ваша класифікація ідеальна. Це спокусливо, якщо ви пишаєтеся своєю роботою, але трудомістким, і це також закінчується тим, що набір правил настільки специфічний, щоб коли-небудь працювати лише для єдиного образу, для якого він був створений. Альтернатива полягає в тому, щоб зберегти більш загальний набір правил, який був недосконалим, але працював досить добре, а потім вручну змінити класифікацію для тих сегментів, які ви знаєте, закінчилися неправильно класифікованими.

Підсумовуючи, об'єктна класифікація зображень є відносно новою методологією, яка спирається на два етапи: 1) поділ зображення на суміжні та однорідні сегменти, а потім 2) класифікація цих сегментів. Він може бути використаний для створення класифікацій зображень, які майже завжди перевершують класифікації на піксель з точки зору точності, але також вимагають значно більше часу для проведення аналітика зображень. Першим, найкращим і найбільш використовуваним програмним забезпеченням для OBIA в області дистанційного зондування є EcoGNition, але інші комерційні програмні пакети, такі як ENVI та Geomatica, також розробили власні модулі OBIA. Пакети програмного забезпечення ГІС, такі як ArcGIS та QGIS, надають інструменти сегментації зображень, а також інструменти, які можна комбінувати для класифікації сегментів, але, як правило, забезпечують менш спрощені робочі процеси OBIA. Крім того, принаймні один пакет програмного забезпечення з відкритим кодом був спеціально розроблений для OBIA, а інструменти сегментації зображень доступні в деяких бібліотеках обробки зображень, таких як OTB.