4.6: Множення дробів

Last updated
Save as PDF

Page ID: 66389

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Модель площі

Однією з наших моделей для множення цілих чисел стала модель площі. Наприклад, твір$23 \times 37$ - площа (кількість квадратів 1 × 1) прямокутника 23 на 37:

$area-model-23-by-37-300x189.png$

Так що добуток двох фракцій, скажімо, також$\frac{4}{7} \times \frac{2}{3}$ повинен відповідати проблемі області.

Приклад: (4/7 × 2/3)

Почнемо з відрізка деякої довжини, який ми називаємо 1 одиницею:

$unitseg-300x16.png$

Тепер побудуйте квадрат, який має по одній одиниці з кожного боку:

$unitsq-300x287.png$

Площа квадрата, звичайно ж,$1 \times 1 = 1$ квадратна одиниця.

Тепер розділимо відрізок зверху на три однакових за розміром шматочки. (Таким чином, кожен шматок є$\frac{1}{3}$.) І розділимо відрізок збоку на сім рівних за розміром шматочків. (Таким чином, кожен шматок є$\frac{1}{7}$.)

$unitsqdiv-300x293.png$

Ми можемо використовувати ці позначки, щоб розділити весь квадрат на маленькі прямокутники рівного розміру. (Кожен прямокутник має одну сторону, яка вимірює,$\frac{1}{3}$ та іншу сторону, яка вимірює$\frac{1}{7}$.)

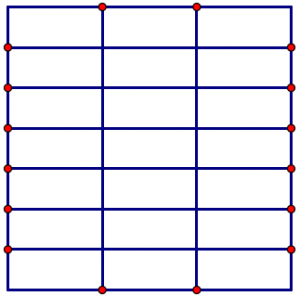
$unitsqdiv2-300x296.png$

Тепер ми можемо відзначити чотири сьомі з одного боку і дві третини з іншого боку.

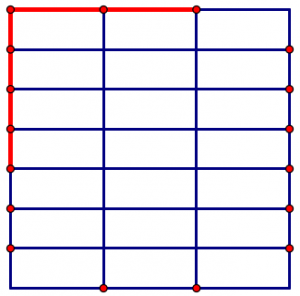
$unitsqdiv3-300x296.png$

Результатом множення повинна стати площа прямокутника з$\frac{4}{7}$ одного і з іншого$\frac{2}{3}$ боку. Що це за область?

$areamodel2-300x297.png$

Пам'ятайте, вся площа була однією одиницею. Цей квадрат розділений на 21 рівний за розміром шматок, а наш прямокутник (той, що має сторони$\frac{4}{7}$ і$\frac{2}{3}$) містить вісім таких прямокутників. Оскільки затінена область є відповіддю на нашу проблему множення, ми робимо висновок, що

\[\frac{4}{7} \times \frac{2}{3} = \frac{8}{21} \ldotp \nonumber \]

Подумайте/Пара/Поділитися

Використовуйте модель для обчислення кожного з наступних продуктів. Намалюйте картинку, щоб чітко побачити відповідь. $$\ розрив {3} {4}\ раз\ frac {5} {6},\ qquad\ frac {3} {8}\ раз\ frac {4} {5},\ qquad\ frac {5} {8}\ час\ frac {3} {7}\ ldotp$$
Задача про площу$\frac{4}{7} \times \frac{2}{3}$ дала діаграму із загальною кількістю 21 малих прямокутників. Поясніть, чому 21 відображається як загальна кількість прямокутників рівного розміру.
Задача області$\frac{4}{7} \times \frac{2}{3}$ дала діаграму з 8 маленькими затіненими прямокутниками. Поясніть, чому 8 відображається як кількість затінених прямокутників.

Проблема 5

Як можна розширити модель площі для дробів більше 1? Спробуйте намалювати картинку для кожного з них:\[\frac{3}{4} \cdot \frac{3}{2}, \qquad \frac{2}{5} \cdot \frac{4}{3}, \qquad \frac{3}{10} \cdot \frac{5}{4}, \qquad \frac{5}{2} \cdot \frac{7}{4} \ldotp \nonumber \]

На свій розсуд

Працюйте над наступними вправами самостійно або з партнером.

Обчислити наступні продукти, максимально спростивши кожен з відповідей. Вам не потрібно малювати фотографії, але ви, безумовно, можете зробити це, якщо це допоможе! $\ розрив {5} {11}\ раз\ frac {7} {12},\ qquad\ frac {4} {7}\ раз\ frac {4} {4} {8},\ qquad\ frac {1} {1},\ qquad\ frac {2} {1}\ раз\ frac {3} {1},\ qquad\ frac {1} {5}\ раз\ frac {5} {1}\ ldotp$$
Обчислити наступні продукти. (Не працюйте занадто старанно!) $\ frac {3} {4}\ раз\ frac {1} {3}\ раз\ frac {2} {5},\ qquad\ frac {5} {5} {5}\ раз\ frac {7} {8},\ qquad\ frac {88} {88}\ раз\ frac {541} {788},\ qquad\ frac {7776} {311}\ раз\ frac {311} {77876}\ ldotp$$
Спробуйте цей. Чи можете ви скористатися правилом дробу,$\frac{xa}{xb} = \frac{a}{b}$ щоб допомогти вам розрахувати? Як? $$\ гідророзриву {1} {2}\ раз\ гідророзриву {2} {3}\ раз\ гідророзриву {3} {4}\ раз\ гідророзриву {4} {5}\ раз\ frac {5} {6}\ раз\ frac {7} {7} {7} {8}\ раз\ frac {8} {8} {9}\ раз\ frac 9} {10}\ ldotp$$

Подумайте/Пара/Поділитися

Чим ці дві проблеми відрізняються? Намалюйте малюнок кожного.

Пем мав$\frac{2}{3}$ торт у холодильнику, і вона$\frac{1}{2}$ з'їла його. Скільки всього пирога вона з'їла?
У понеділок Пем$\frac{2}{3}$ з'їла торт. У вівторок Пем$\frac{1}{2}$ з'їла торт. Обидва коржа були однакового розміру. Скільки всього пирога вона з'їла?

Коли проблема включає фразу на кшталт «$\frac{2}{3}$з...», учнів навчають розглядати «of» як множення, і використовувати це для вирішення проблеми. Як показують перераховані вище проблеми, в деяких випадках це має сенс, а в деяких випадках - ні. Важливо уважно читати і розуміти, про що задається проблема, а не запам'ятовувати правила про «переклад» проблем слів.

Пояснення правила

Ви, ймовірно, спростили свою роботу у вправах вище, використовуючи правило множення, як показано нижче.

Множення дробів

\[\frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d} \ldotp \nonumber \]

Звичайно, ви можете вибрати спрощення остаточної відповіді, але відповідь завжди еквівалентна цій. Чому? Модель площі може допомогти нам пояснити, що відбувається.

По-перше, давайте чітко випишемо, як модель площі говорить множити$\frac{a}{b} \cdot \frac{c}{d}$. Ми хочемо побудувати прямокутник, де одна сторона має довжину,$\frac{a}{b}$ а інша сторона має довжину$\frac{c}{d}$. Починаємо з квадрата, по одній одиниці з кожного боку.

Розділіть верхній відрізок на $б$ однакові за розміром шматочки. $a$ Відтінок цих шматочків. (Це буде сторона прямокутника з довжиною$\frac{a}{b}$.)
Розділіть лівий відрізок на $d$ однакові за розміром шматочки. $c$ Відтінок цих шматочків. (Це буде сторона прямокутника з довжиною$\frac{c}{d}$.)
Розділіть весь прямокутник відповідно до галочками з боків, зробивши прямокутники рівного розміру.
Затіньте прямокутник, обмежений затіненими сегментами.

Якщо відповідь є$\frac{a \cdot c}{b \cdot d}$, це означає, що в квадраті є$b \cdot d$ загальні однакові шматочки, і$a \cdot c$ з них затінені. З моделі ми бачимо, чому це так:

Верхній сегмент був розділений на $б$ однакові за розміром шматочки. Таким чином, є $б$ стовпці в прямокутник.
Бічний сегмент був розділений на $d$ однакові за розміром шматочки. Таким чином, є $d$ рядки в прямокутник.
Прямокутник зі $б$ стовпцями і $d$ рядками має$b \cdot d$ шматочки. (Модель площі для множення цілого числа!)

Подумайте/Пара/Поділитися

Дотримуйтеся загального правила множення

\[\frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d} \ldotp \nonumber \]

Напишіть чітке пояснення, чому$a \cdot c$ з маленьких прямокутників будуть затінені.

Множення дробів на цілі числа

Часто учнів початкових класів вчать множити дроби на цілі числа за допомогою правила дробу.

Приклад: Множення дробів

Наприклад, щоб помножити$2 \cdot \frac{3}{7}$, ми думаємо про «2» як$\frac{2}{1}$ і обчислюємо таким чином\[2 \cdot \frac{3}{7} = \frac{2}{1} \cdot \frac{3}{7} = \frac{2 \cdot 3}{1 \cdot 7} = \frac{6}{7} \ldotp \nonumber \]

Ми також можемо думати з точки зору нашої оригінальної моделі «Пироги на дитину», щоб відповісти на такі запитання.

Приклад: Пироги на дитину

Ми знаємо, що$\frac{3}{7}$ означає кількість пирога кожна дитина отримує, коли 7 дітей рівномірно поділяють 3 пироги.

Якщо ми обчислюємо це означає$2 \cdot \frac{3}{7}$, що ми подвоїти кількість пирога кожен дитина отримує. Ми можемо зробити це, подвоївши кількість пирогів. Отже, відповідь така ж, як$\frac{6}{7}$: кількість пирога кожна дитина отримує, коли 7 дітей рівномірно поділяють 6 пирогів.

Нарешті, ми можемо думати з точки зору одиниць і об'єднання.

Приклад: Одиниці

Дріб$\frac{3}{7}$ означає, що у мене 7 рівних штук (чогось), а я беру 3 з них.

Так$2 \cdot \frac{3}{7}$ значить, зробити це двічі. Якщо я візьму 3 штуки, а потім знову 3 штуки, то отримую в цілому 6 штук. Є ще 7 рівних штук в цілому, так що відповідь є$\frac{6}{7}$.

Подумайте/Пара/Поділитися

Скористайтеся всіма трьома методами, щоб пояснити, як знайти кожен продукт: $3\ cdot\ frac {2} {5},\ qquad 4\ cdot\ frac {3} {8},\ qquad 6\ cdot\ frac {1} {5}\ ldotp$$
Порівняйте ці різні способи мислення про множення дробів. Чи є хтось із них більш природним для вас? Чи один має більше сенсу, ніж інші? Чи впливають конкретні цифри в проблемі на вашу відповідь? Чи згоден ваш партнер?

Пояснення правила ключового дробу

Рой каже, що правило фракції

\[\frac{xa}{xb} = \frac{a}{b} \nonumber \]

є «очевидним», якщо ви думаєте з точки зору множення дробів. Він міркує наступним чином:

Ми знаємо, що множення чогось на 1 не змінює число:

\[\begin{split} 1 \cdot 4 &= 4 \\ 1 \cdot 2014 &= 2014 \\ 1 \cdot \frac{5}{7} &= \frac{5}{7} \end{split} \nonumber \]

Отже, загалом,

\[1 \cdot \frac{a}{b} = \frac{a}{b} \ldotp \nonumber \]

Тепер$\frac{2}{2} = 1$, так що це означає, що

\[\frac{2}{2} \cdot \frac{a}{b} = 1 \cdot \frac{a}{b} = \frac{a}{b}, \nonumber \]

що означає

\[\frac{2a}{2b} = \frac{a}{b} \ldotp \nonumber \]

За тими ж міркуваннями$\frac{3}{3} = 1$, так що це означає, що

\[\frac{3}{3} \cdot \frac{a}{b} = 1 \cdot \frac{a}{b} = \frac{a}{b}, \nonumber \]

що означає

\[\frac{3a}{3b} = \frac{a}{b} \ldotp \nonumber \]

Подумайте/Пара/Поділитися

Що ви думаєте про міркування Роя? Чи має сенс? Як би Рой пояснив загальне правило для позитивних цілих чисел $х$ :

\[\frac{xa}{xb} = \frac{a}{b} ? \nonumber \]