3.3: Операції над множинами

Є кілька важливих способів того, що новий набір можна зробити з наборів, які у вас вже є. Будь-який спосіб зробити це називається операцією набору.

3.3А. Союз і перетин.

Дві з найбільш основних операцій - об'єднання і перетин. Давайте спочатку обговоримо їх в неформальному плані. Припустимо:

• Аліса і Боб збираються влаштувати вечірку, і потрібно вирішити, кого слід запросити,
• Аліса склала список всіх людей, яких вона хотіла б запросити, і
• Боб склав список всіх людей, яких хотів би запросити.

Ось два з багатьох можливих рішень, які вони могли б прийняти.

1. Одним з рішень було б запросити всіх, хто знаходиться в будь-якому зі списків. Тобто вони могли почати свій список запрошень, записуючи всі імена в списку Аліси, а потім додати всі імена зі списку Боба (або, точніше, імена зі списку Боба, які ще не включені до списку Аліси). Це об'єднання списків.
2. Набагато більш консервативним рішенням було б запросити лише тих людей, які фігурують в обох списках. Тобто вони могли пройти список Аліси, і перекреслити всіх, хто не відображається в списку Боба. (Вони отримали б той самий результат, переглянувши список Боба, і перекресливши всіх, хто не відображається в списку Аліси.) Це перетин списків.

Визначення\(3.3.1\).

Припустимо\(A\) і\(B\) є множинами.

1. Об'єднання\(A\) і\(B\) є безліччю\[A \cup B=\{x \mid x \in A \text { or } x \in B\} .\]
2. Перетин\(A\) і\(B\) є множиною\[A \cap B = \{A \cap B=\{x \mid x \in A \text { and } x \in B\} .\]

Зауваження\(3.3.2\).

Малюючи множини\(A\) і\(B\) як перекриваються кола, об'єднання і перетин можна представити наступним чином:

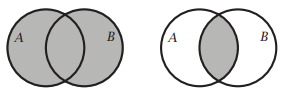
\(A \cup B\)\(A \cap B\)затінюється, затінюється

Такі малюнки називаються діаграмами Венна.

Зауваження\(3.3.3\).

1. У звичайній англійській мові слово «перетин» позначає те, де зустрічаються дві речі. Наприклад, перетин двох вулиць - це місце, де дві вулиці збираються разом. Ми можемо думати, що ця область є частиною обох вулиць, тому це узгоджується з тим, як цей термін використовується в математиці.
2. У звичайній англійській мові слово «союз» позначає об'єднання речей разом. Наприклад, шлюб — це союз двох людей — він об'єднує двох людей в єдину подружню пару. Це узгоджується з тим, як цей термін використовується в математиці - ми могли б сформувати об'єднання списку Аліси та списку Боба, приклеївши список Боба до кінця списку Аліси.

Приклад\(3.3.4\).

1. \(\{1,3,5,7,9\} \cup \{1,4,7,10\} = \{1,3,4,5,7,9,10\}\)
2. \(\{1,3,5,7,9\} \cap \{1,4,7,10\} = \{1,7\}\)

Рішення

Додайте сюди текст.

Вправа\(\PageIndex{1}\)

Вкажіть кожен набір, перерахувавши його елементи. (Не потрібно показувати свою роботу. )

1. \(\{1,2,3,4\} \cup\{3,4,5,6,7\}=\)
2. \(\{1,2,3,4\} \cap\{3,4,5,6,7\}=\)
3. \(\{\mathrm{p}, \mathrm{r}, \mathrm{o}, \mathrm{n}, \mathrm{g}\} \cap\{\mathrm{h}, \mathrm{o}, \mathrm{r}, \mathrm{n}, \mathrm{s}\}=\)
4. \(\{\mathrm{p}, \mathrm{r}, \mathrm{o}, \mathrm{n}, \mathrm{g}\} \cup\{\mathrm{h}, \mathrm{o}, \mathrm{r}, \mathrm{n}, \mathrm{s}\}=\)
5. \((\{1,3,5\} \cup\{2,3,4\}) \cap\{2,4,6\}=\)
6. \((\{1,3,5\} \cap\{2,3,4\}) \cup\{2,4,6\}=\)

Вправа\(3.3.6\).

1. Припустімо\(A\) і\(B\) є множинами. Доведіть, що якщо\(c \in A \cap B\), то\(c \in A\).
2. Припустимо\(X\),\(Y\), і\(Z\) є множинами. Доведіть, що якщо\(r \in (X \cap Y) \cup (X \cap Z)\), то\(r \in X\).

Зауваження\(3.3.7\).

1. Це не важко побачити, що\(\cup\) і\(\cap\) є комутативними. Тобто для всіх наборів\(A\) і\(B\), у нас є\[A \cup B=B \cup A \quad \text { and } \quad A \cap B=B \cap A\]

2. Також неважко помітити, що\(\cup\) і\(\cap\) асоціативні. Тобто, для всіх наборів\(A\), і\(B\)\(C\), у нас є\[(A \cup B) \cup C=A \cup(B \cup C) \quad \text { and } \quad(A \cap B) \cap C=A \cap(B \cap C)\]
   Так що немає необхідності в дужках при написанні\(A \cup B \cup C\) або\(A \cap B \cap C\). (Однак вам потрібні дужки при написанні чогось подібного\(A \cup (B \cap C)\) або\((A \cup B) \cap C\), який використовує обидва\(\cup\) і\(\cap\).)

Приклад\(3.3.8\).

Діаграма Венна може включати більше двох наборів. Наприклад, ось діаграми Венна\(A \cap B \cap C\) і\(A \cap (B \cup C)\).

\(A \cap B \cap C\)\(A \cap (B \cup C)\)затінюється, затінюється

Рішення

Додайте сюди текст.

Вправа\(3.3.9\).

Намалюйте схему Венна кожного набору. (Не потрібно показувати свою роботу. )

1. \(A \cup B \cup C\)
2. \(A \cup(B \cap C)\)
3. \((A \cup B) \cap C\)
4. \((A \cap C) \cup(B \cap C)\)

Відповідь

Додайте сюди тексти. Не видаляйте цей текст спочатку.

3.3Б. Встановити різницю та доповнення

«Встановлена різниця» - ще одна фундаментальна операція.

Приклад\(3.3.10\).

Якщо є список людей, яких Аліса хотіла б запросити на вечірку, а також список людей, яких Боб відмовляється дозволити приходити на вечірку («список вето»), то розумно було б запросити людей, які знаходяться в списку Аліси, але не в списку вето. Тобто, вони могли б почати зі списку Аліси, і видалити всі імена, які є у списку Боба. Це встановлена різниця списку Аліси та списку Боба.

Визначення\(3.3.11\).

Припустимо\(A\) і\(B\) є множинами.

1. Встановлена різниця\(A\) і\(B\) є набором\[A \backslash B=\{x \in A \mid x \notin B\}=\{x \mid(x \in A) \&(x \notin B)\} .\]

2. Доповненням\(B\) є набір,\[\bar{B}=\mathcal{U} \backslash B=\{x \mid x \notin B\}\]
   де\(\mathcal{U}\) знаходиться універсальний набір, як зазвичай.

Інші позначення.

Деякі автори пишуть\(A - B\), замість\(A \backslash B\). Також деякі автори пишуть\(B^{c}\), замість\(\bar{B}\)

Зауваження\(3.3.12\).

Ось діаграми Венна.

\(A \backslash B\)\(B \backslash A\)затінюється, затінюється

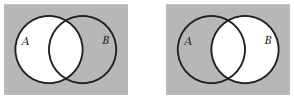
\(\bar{A}\)\(\bar{B}\)затінюється, затінюється

Приклад\(3.3.13\).

Припустимо,\(\mathcal{U}=\mathrm{PEOPLE}\) це сукупність всіх людей.

1. \(\overline{\text { CHILDREN }}=\text { ADULTS }\), тому що дорослі - це люди, які не є дітьми.
2. \(\text { FEMALES } \backslash \text { CHILDREN }\)є сукупністю всіх дорослих жінок.

Вправа\(3.3.14\).

Припустимо\(\mathcal{U}=\{1,2,3, \ldots, 10\}\). Вкажіть кожен набір, перерахувавши його елементи. (Не потрібно показувати свою роботу. )

1. \(\{1,3,5,7,9\} \backslash\{4,5,6,7\}=\)
2. \(\{4,5,6,7\} \backslash\{1,3,5,7,9\}=\)
3. \(\overline{\{1,3,5,7,9\}}=\)
4. \(\overline{\{4,5,6,7\}}=\)

Вправа\(3.3.15\).

Намалюйте схему Венна кожного набору. (Не потрібно показувати свою роботу. )

1. \(\overline{A \cup B}\)
2. \(\overline{A \cap B}\)
3. \((A \vee B) \backslash(A \vee C)\)
4. \(A \backslash(B \backslash C)\)
5. \((A \cup B) \backslash C\)

Приклад\(3.3.16\).

Припустимо\(A\) і\(B\) є множинами. Покажіть, що якщо\(c \in \overline{A \cup B}\), то\(c \in \bar{A} \cap \bar{B}\).

Рішення

Припустимо\(c \in \overline{A \cup B}\). За визначенням комплементу це означає\(c \notin A \cup B\). Іншими словами, це неправда\(c \in A \cup B\). З визначення\(A \cup B\), зробимо висновок, що\[\text { it is not true that either } c \in A \text { or } c \in B \text {. }\]
За правилами заперечення це означає\(c \notin A\) і\(c \notin B\). Зараз:

• з тих пір\(c \notin A\), у нас є\(c \in \bar{A},\), і
• з тих пір\(c \notin B\), у нас є\(c \in \bar{B}\).

Тому ми знаємо\(c \in \bar{A}\) і\(c \in \bar{B}\), так\(c \in \bar{A} \cap \bar{B}\).

Вправа\(3.3.17\).

Припустимо\(A\) і\(B\) є множинами. Покажіть, що якщо\(c \in \bar{A} \cap \bar{B}\), то\(c \in \overline{A \cup B}\).

3.3C. Роз'єднані набори

Визначення\(3.3.18\).

Два\(B\) множини\(A\) і, як кажуть, нез'єднані, якщо їх перетин порожній (тобто\(A \cap B=\varnothing\)). Іншими словами, вони не мають спільних елементів:\ [A\ text {і} B\ text {нез'єднані}\ Leftrightarrow\ begin {зібрався}
\ text {не існує} x,
\\ text {такий, що} ((x\ in A)\ & (x\ in B)).
\ end {graeded}\]
Ми також можемо сказати, що\(A\) є нез'єднаним з B.

Приклад\(3.3.19\).

1. Набори\(\{1,3,5\}\) і\(\{2,4,6\}\) є нероз'ємними, тому що не мають спільних елементів.
2. Множини\(\{1,3,5\}\) і\(\{2,3,4\}\) не розмежовуються, тому що\(3\) знаходиться в їх перетині.
3. Наступна діаграма Венна ілюструє два нез'єднаних\(B\) множини\(A\) і (вони не перекриваються):

\(A\)і\(B\) розмежовуються

Зауваження\(3.3.20\).

Відзначимо деякі відомі факти, які будуть офіційно доведені в розділі\(9\).

1. Якщо\(A\) і\(B\) є двома нероз'єднаними множинами, то\(\#(A \cup B)=\# A+\# B\).
2. Ситуація схожа, навіть якщо\(2\) множин більше: Припустимо, що\(A_1,A_2,\ldots,A_n\) це попарно-нез'єднані множини. (Це означає, що\(A_i\) від'єднується від\(A_j\) кожного разу\(i \neq j\).) Тоді\[\#\left(A_{1} \cup A_{2} \cup \cdots \cup A_{n}\right)=\# A_{1}+\# A_{2}+\cdots+\# A_{n} .\]
3. Якщо\(A\) і\(B\) є двома скінченними множинами, які не розмежовуються, то\(\#(A \cup B)<\# A+\# B\).

3.3D. Набір потужності.

Приклад\(3.3.21\).

Не складно перерахувати всі підмножини\(\{a,b,c\}\). Один із способів зробити це - розглянути можливу кількість елементів у підмножині:

0. Підмножина з\(0\) елементами взагалі не має елементів. Це повинен бути порожній набір\(\varnothing\).
1. Розглянемо підмножину з\(1\) елементом. Саме один елемент повинен бути одним з елементів\(\{a,b,c\}\). Тобто елемент набору повинен бути\(a\)\(b\), або\(c\). Таким чином, 1-елементні\(\{a\}\) підмножини є\(\{b\}\), і\(\{c\}\).
2. Розглянемо підмножини з\(2\) елементами.
   • Якщо\(a\) є одним з елементів у підмножині, то інший елемент повинен бути або\(b\) або\(c\).
   • Якщо\(a\) немає в підмножині, то підмножина повинна містити обидва\(b\) і\(c\).

   Отже,\(2\) підмножини\(\{a,b\}\) -element є\(\{a,c\}\), і\(\{b,c\}\).

3. Підмножина з\(3\) елементами повинна мати всі елементи\(\{a,b,c\}\), тому підмножина повинна бути\(\{a,b,c\}\).
4. Тому що\(\{a,b,c\}\) має тільки\(3\) елементи, ми знаємо, що жоден підмножина не може мати більше, ніж\(3\) елементи.

Таким чином, підмножини\(\{a,b,c\}\) є\[\varnothing,\{a\},\{b\},\{c\},\{a, b\},\{a, c\},\{b, c\},\{a, b, c\} .\]
Підрахунок їх, ми бачимо, що є точно\(8\) підмножини.

Зауваження\(3.3.22\).

Загалом, можна показати, що будь-який набір з\(n\) елементами має саме\(2^{n}\) підмножини. У наведеному вище прикладі ми маємо\(n = 3\), і кількість підмножин є\(2^{3} = 8\).

Вправа\(3.3.23\).

(Не потрібно показувати свою роботу. )

1. Перерахуйте підмножини\(\{a\}\).
2. Перерахуйте підмножини\(\{a,b\}\).
3. Перерахуйте підмножини\(\{a,b,c,d\}\).
4. Перерахуйте підмножини\(\varnothing\).

Ми можемо зробити множину, поставивши набір фігурних дужок в кінці наведеного вище списку підмножин\(\{a,b,c\}\):\[\{\varnothing,\{a\},\{b\},\{c\},\{b, c\},\{a, c\},\{a, b\},\{a, b, c\}\} .\]
Загалом, множина всіх підмножин множини називається його множиною потужності:

Визначення\(3.3.24\).

Припустимо,\(A\) це набір. Набір потужності\(A\) - це множина всіх підмножин\(A\). Воно позначається\(\mathcal{P}(A)\). Це означає\[\mathcal{P}(A)=\{B \mid B \subset A\} .\]

Зауваження\(3.3.25\).

З зауваження\(3.3.22\)., Ми бачимо, що якщо\(\#A = n\), то\(\# \mathcal{P}(A)=2^{n}\). Цю формулу, яка передбачає «\(n\)два-на-ту- владу», можна вважати обґрунтуванням для\(\mathcal{P}(A)\) виклику набору потужності.

Вправа\(3.3.26\).

1. Опишіть кожен з наступних наборів, перерахувавши його елементи.
   (Не потрібно показувати свою роботу. )
   1. \(\mathcal{P}(\varnothing)\)
   2. \(\mathcal{P}(\{\mathrm{a}\})\)
   3. \(\mathcal{P}(\{\mathrm{a}, \mathrm{b}\})\)
   4. \(\mathcal{P}(\{\mathrm{a}, \mathrm{b}, \mathrm{c}\})\)
   5. \(\mathcal{P}(\{\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}\})\)
2. Які з перерахованих нижче елементів\(\mathcal{P}(\{\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}\})\)?
   (Не потрібно показувати свою роботу. )
   1. \(a\)
   2. \(\{\mathrm{a}\}\)
   3. \(\{a, b\}\)
   4. \(\{\mathrm{a}, \mathrm{c}\}\)
3. Припустимо,\(A\) це набір.
   1. Є\(\varnothing \in \mathcal{P}(A)\)? Чому?
   2. Є\(A \in \mathcal{P}(A)\)? Чому?
4. Чи існує набір\(A\), такий що\(\mathcal{P}(A)=\varnothing\)?
5. Нехай\[V_{0}=\varnothing, \quad V_{1}=\mathcal{P}\left(V_{0}\right), \quad V_{2}=\mathcal{P}\left(V_{1}\right)=\mathcal{P}\left(\mathcal{P}\left(V_{0}\right)\right), \quad \text { and so forth. }\]
   взагалі,\(V_{n}=\mathcal{P}\left(V_{n-1}\right)\) коли завгодно\(n > 0\).
   1. Які кардинальності\(V_{0}\),,\(V_{1}\),\(V_{2}\),\(V_{3}\)\(V_{4}\), і\(V_{5}\)?
   2. Опишіть\(V_{0}\)\(V_{1}\),\(V_{2}\),, і\(V_{3}\) перерахувавши їх елементи.
   3. (Складніше) Опишіть\(V_{4}\), перерахувавши його елементи.
   4. Чи розумно попросити когось перерахувати елементи\(V_{5}\)? Чому?