4.1: Найменші квадрати
- Page ID
- 62908
Вступ
Ми дізналися в попередньому розділі, що не\(Ax = b\) потрібно володіти розв'язком, коли кількість рядків\(A\) перевищує його ранг, т\(r < m\). Оскільки така ситуація виникає досить часто на практиці, як правило, під виглядом «більше рівнянь, ніж невідомих», ми встановлюємо обґрунтування абсурду\(Ax = b\).
Нормальні рівняння
Мета полягає в тому, щоб вибрати\(x\) таку,\(Ax\) яка максимально наближена до\(b\). Вимірюючи близькість через суму квадратів складових, ми приходимо до задачі мінімізації «найменших квадратів»
res
\[(||Ax-b||)^2 = (Ax-b)^{T}(Ax-b) \nonumber\]
над усім\(x \in \mathbb{R}\). Шляху до розв'язку висвітлює фундаментальна теорема. Точніше, пишемо
\(\forall b_{R}, b_{N}, b_{R} \in \mathbb{R}(A) \wedge b_{N} \in \mathbb{N} (A^{T}) : (b = b_{R}+b_{N})\). Відзначивши, що (i)\(\forall b_{R}, x \in \mathbb{R}^n : ((Ax-bR) \in \mathbb{R}(A))\) і (ii)\(\mathbb{R}(A) \perp \mathbb{N} (A^T)\) ми приходимо до теореми Піфагора.
\[norm^{2}(Ax-b) = (||Ax-b_{R}+b_{N}||)^2 \nonumber\]
\[= (||Ax-b_{R}||)^2+(||b_{N}||)^2 \nonumber\]
З теореми Піфагора тепер зрозуміло, що найкращим\(x\) є той, який задовольняє
\[Ax = b_{R} \nonumber\]
Оскільки\(b_{R} \in \mathbb{R}(A)\) це рівняння дійсно має рішення. Однак ми ще не вказуємо, як один обчислює\(b_{R}\) дані\(b\). Хоча явний вираз для\(b_{R}\) ортогональної проекції\(b\) на\(\mathbb{R}(A)\), з точки зору\(A\) і\(b\) знаходиться в межах нашої досяжності, ми, строго кажучи, не вимагатимемо цього. Щоб побачити це, зауважимо, що якщо\(x\) задовольняє вищевказане рівняння, то \(b\)ортогональна проекція на\(\mathbb{R}(A)\), з точки зору\(A\) і\(b\) знаходиться в межах нашої досяжності, ми, строго кажучи, не вимагатимемо цього. Щоб переконатися в цьому, зауважимо, що якщо\(x\) задовольняє вищевказаному рівнянню, то
\[Ax-b = Ax-b_{R}+b_{N} \nonumber\]
\[= -b_{N} \nonumber\]
Як\(b_{N}\) це не легше обчислюється, ніж\(b_{R}\) ви можете стверджувати, що ми просто йдемо по колу. Однак «практична» інформація у вищенаведеному рівнянні полягає в тому\((Ax-b) \in A^{T}\), що\(A^{T}(Ax-b) = 0\), тобто,
\[A^{T} Ax = A^{T} b \nonumber\]
Оскільки\(A^{T} b \in \mathbb{R} (A^T)\) незалежно від\(b\) цієї системи, часто називають нормальними рівняннями, дійсно має рішення. Це рішення є унікальним до тих пір, поки\(A^{T}A\) стовпці лінійно незалежні, тобто так довго, як\(\mathbb{N}(A^{T}A) = {0}\). Згадуючи главу 2, вправу 2, зауважимо, що це еквівалентно\(\mathbb{N}(A) = \{0\}\)
Набір,\(x \in b_{R}\) для якого невідповідність\((||Ax-b||)^2\) найменша, складається з тих,\(x\) для яких завжди\(A^{T}Ax = A^{T}b\) є хоча б один такий\(x\). Є рівно один такий\(x\) якщо\(\mathbb{N}(A) = \{0\}\).
Як конкретний приклад, припустимо з посиланням на рис. 1, що\(A = \begin{pmatrix} {1}&{1}\\ {0}&{1}\\ {0}&{0} \end{pmatrix}\) і\(A = \begin{pmatrix} {1}\\ {1}\\ {1} \end{pmatrix}\)
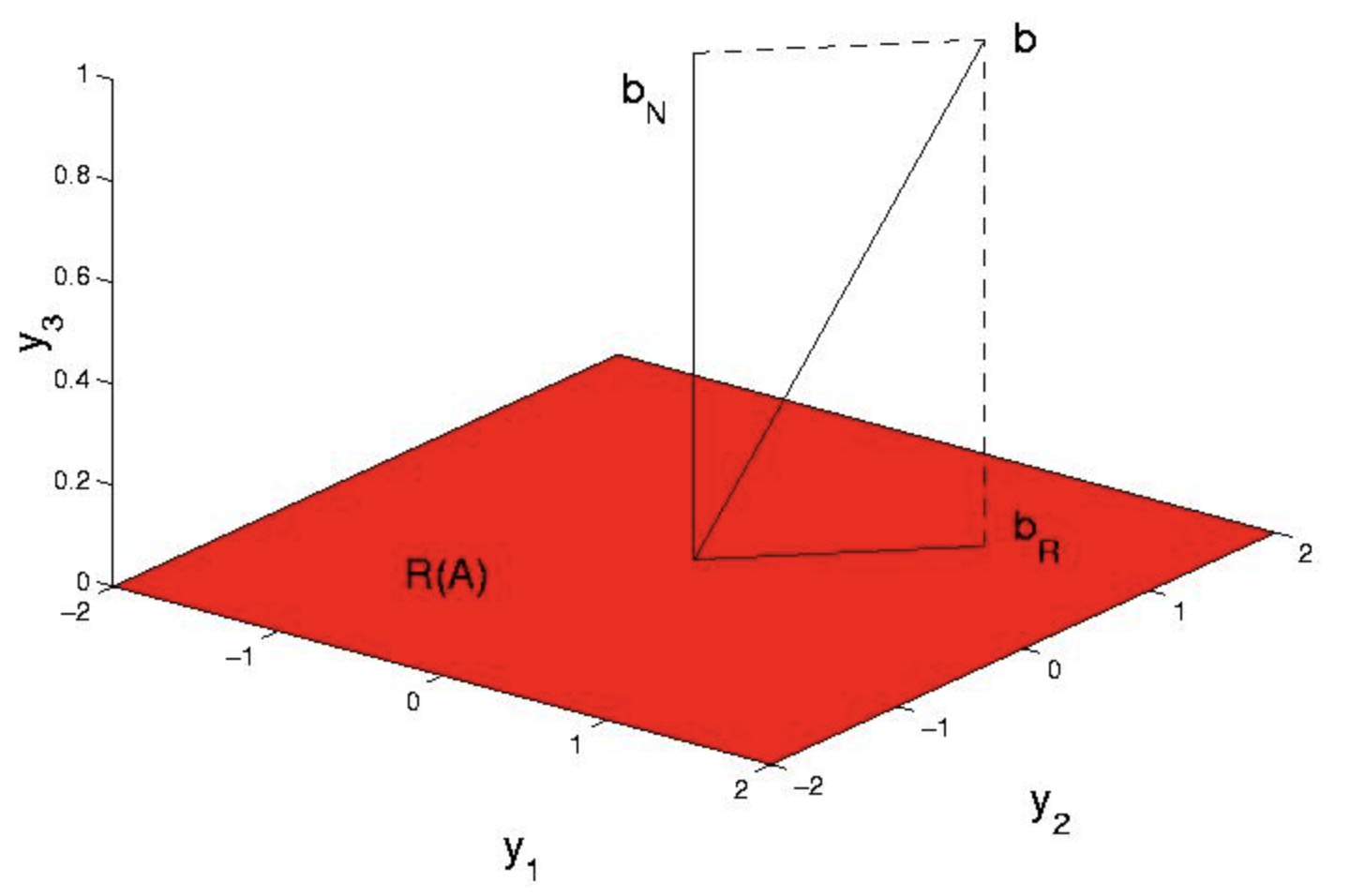
Як\(b \ne \mathbb{R}(A)\) немає\(x\) такого, що\(Ax = b\). Дійсно\((||Ax-b||)^2 = (x_{1}+x_{2}+-1)^2+(x_{2}-1)^2+1 \ge 1\), при мінімумі однозначно досягається при\(x = \begin{pmatrix} {0}\\ {1} \end{pmatrix}\), згідно з унікальним рішенням вищевказаного рівняння, для\(A^{T} A = \begin{pmatrix} {1}&{1}\\ {1}&{2} \end{pmatrix}\) і\(A^{T} b = \begin{pmatrix} {1}\\ {2} \end{pmatrix}\). Тепер ми визнаємо, апостеріорі,\(b_{R} = Ax = \begin{pmatrix} {1}\\ {1}\\ {0} \end{pmatrix}\) це ортогональна проекція b на простір стовпців\(A\).
Застосування найменших квадратів до двовісної тестової задачі
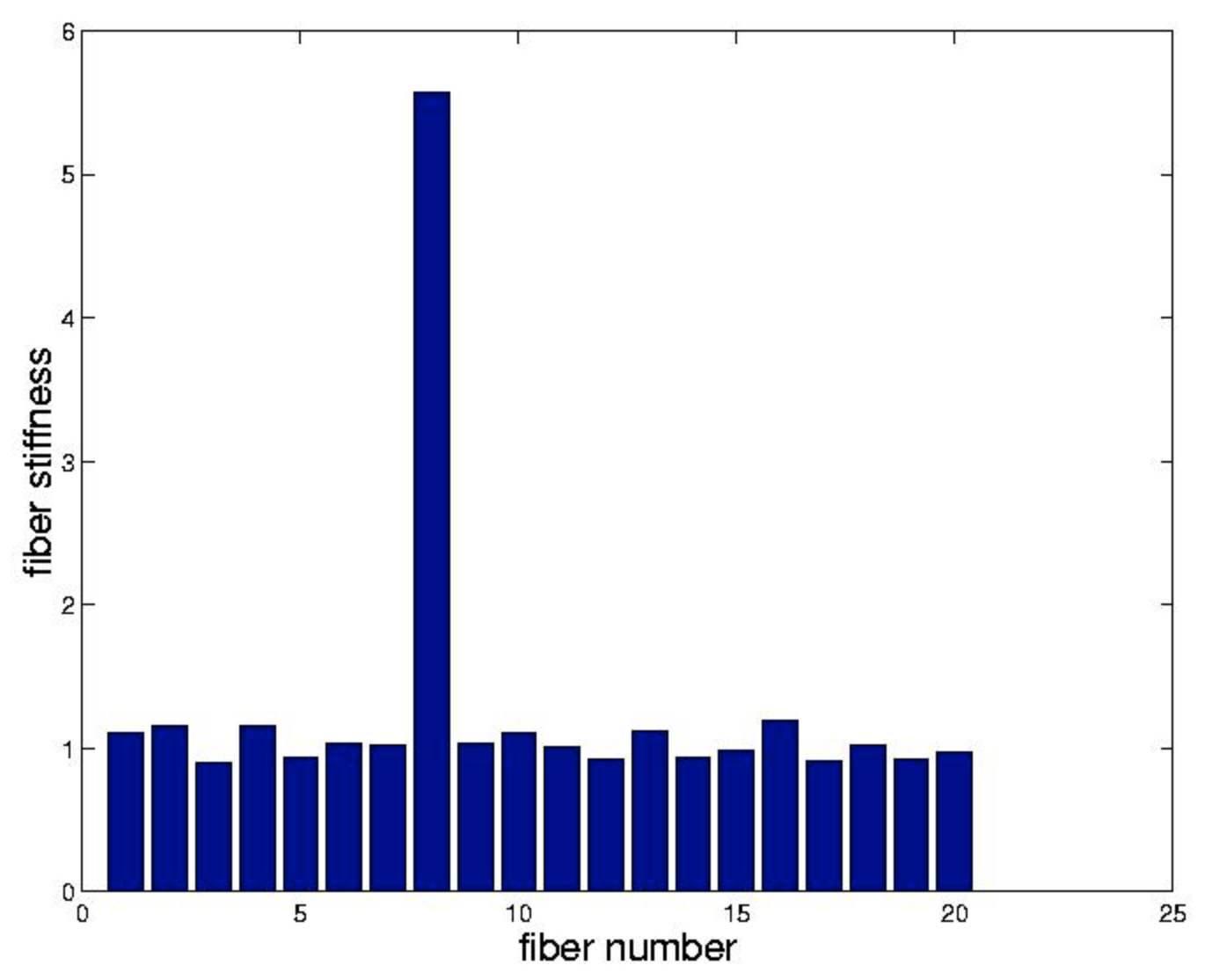
Ми сформулюємо ідентифікацію жорсткості волокна 20 на цьому попередньому малюнку, як задачу найменших квадратів. Ми передбачаємо навантаження, вузли 9 та вимірювання пов'язаних з ними переміщень 18,\(x\). \(x\)Зі знань і\(f\) ми хочемо зробити висновок про компоненти\(K=diag(k)\) де\(k\) знаходиться вектор невідомих жорсткості волокон. Першим кроком є визнання цього
\[A^{T}KAx = f \nonumber\]
може бути написано як
\[\forall B, B = A^{T} diag(Ax) : (Bk = f) \nonumber\]
Хоча концептуально просто це не дуже корисно на практиці, бо\(B\) є 18 на 20 і, отже, вищевказане рівняння має багато рішень. Виходом з ситуації є обчислення в\(k\) результаті не одного експерименту. Ми побачимо, що для нашого невеликого зразка вистачить 2 експериментів. Якщо бути точним, ми припускаємо, що\(x^1\) це переміщення, вироблене навантаженням,\(f^1\) тоді як\(x^2\) це переміщення, вироблене навантаженням\(f^2\). Потім ми збираємо пов'язані шматки в
\[B = \begin{pmatrix} {A^{T} \text{diag} (Ax^1)}\\ {A^{T} \text{diag} (Ax^2)} \end{pmatrix}\]
і
\[f= \begin{pmatrix} {f^1}\\ {f^2} \end{pmatrix}.\]
\(B\)Це 36 на 20, і тому система\(Bk = f\) завищена і, отже, дозріла для найменших квадратів.
Приступаємо потім до збірки\(B\) і\(f\). Припускаємо\(f^{1}\) і\(f^{2}\) відповідати горизонтальному і вертикальному розтягуванню
\[f^{1} = \begin{pmatrix} {-1}&{0}&{0}&{0}&{1}&{0}&{-1}&{0}&{0}&{0}&{1}&{0}&{-1}&{0}&{0}&{0}&{1}&{0} \end{pmatrix}^{T} \nonumber\]
\[f^{2} = \begin{pmatrix} {0}&{1}&{0}&{1}&{0}&{1}&{0}&{1}&{0}&{1}&{0}&{1}&{0}&{-1}&{0}&{-1}&{0}&{-1} \end{pmatrix}^{T} \nonumber\]
відповідно. Для цілей нашого прикладу ми припускаємо, що кожен\(k_{j} = 1\) крім\(k_{8} = 5\). Збираємо\(A^{T}KA\) як у главі 2 і вирішуємо
\[A^{T}KAx^{j} = f^{j} \nonumber\]
за допомогою псевдозворотного. Для того, щоб надати деяку «реальність» цій проблемі, ми забруднимо кожен\(x^{j}\) з 10-відсотковим шумом перед будівництвом\(B\)
\[B^{T}Bk = B^{T}f \nonumber\]
ми зауважимо, що Matlab вирішує цю систему, коли представлена з K=b\ f, коли BB прямокутний. Результати цієї процедури ми побудували за посиланням. Жорстке волокно легко ідентифікується.
Проекції
З алгебраїчної точки зору Рівняння є елегантною переформулюванням задачі найменших квадратів. Хоча легко запам'ятати це, на жаль, затьмарює геометричний зміст, запропонований словом «проекція» Рівняння. Оскільки прогнози часто виникають у багатьох додатках, ми робимо паузу тут, щоб розробити їх більш ретельно. Відносно нормальних рівнянь відзначимо, що якщо\(\mathbb{N}(A) = \{0\}\) тоді
\[x = (A^{T}A)^{-1} A^{T} b \nonumber\]
і тому ортогональна проекція bb на\(\mathbb{R}(A)\) це:
\[b_{R}= Ax \nonumber\]
\[= A (A^{T}A)^{-1} A^T b \nonumber\]
Визначення
\[P = A (A^{T}A)^{-1} A^T \nonumber\]
набуває форму\(b_{R} = Pb\). Сумісно з нашим уявленням про те, якою має бути «проекція», ми очікуємо, що вектори\(P\) карти не\(\mathbb{R}(A)\) потрапляють на,\(\mathbb{R}(A)\) залишаючи вектори вже\(\mathbb{R}(A)\) неушкодженими. Більш лаконічно, ми очікуємо,\(Pb_{R} = b_{R}\) що т\(Pb_{R} = Pb_{R}\). Як останнє повинно триматися для всіх,\(b \in R^{m}\) ми очікуємо, що
\[P^2 = P \nonumber\]
Ми вважаємо, що дійсно
\[P^2 = A (A^{T}A)^{-1} A^T A (A^{T}A)^{-1} A^T \nonumber\]
\[= A (A^{T}A)^{-1} A^T \nonumber\]
\[= P \nonumber\]
Відзначимо також,\(P\) що симетрична. Ми високо оцінимо ці властивості через
Матриця\(P\), яка\(P^2 = P\) задовольняє, називається проекцією. Симетрична проекція називається ортогональної проекцією.
Ми доклали певних зусиль, щоб мотивувати використання слова «проекція». Однак вам може бути цікаво, яке симетрія має відношення до ортогональності. Ми пояснюємо це з точки зору тавтології
\[b = Pb−Ib \nonumber\]
Тепер, якщо\(P\) проекція, то так теж є\(I-P\). Крім того, якщо\(P\) симетричний, то крапковий добуток\(b\).
\ [\ почати {вирівнювати*} (Пб) ^Т (І-П) б &= б ^ {Т} Р^ {Т} (I-P) b\\ [4pt] &= b^ {T} (Р-Р^ {2}) б\\ [4pt] &= b^ {T} 0 б\\ [4pt] &= 0\ кінець {вирівнювати*}
тобто,\(Pb\) є ортогональним до\((I-P)b\). Як приклади неортогональних проекцій ми пропонуємо
\[P = \begin{pmatrix} {1}&{0}&{0}\\ {\frac{-1}{2}}&{0}&{0}\\ {\frac{-1}{4}}&{\frac{-1}{2}}&{1} \end{pmatrix}\]
і\(I-P\). Нарешті, відзначимо, що центральна формула\(P = A (A^{T}A)^{-1} A^T\), навіть трохи більш загальна, ніж рекламована. Він був виставлений рахунком як ортогональна проекція на простір колон\(A\). Однак часто виникає необхідність ортогональної проекції на якийсь довільний підпростір М. Ключем до використання старого РР є просто усвідомити, що кожен підпростір є простором стовпців деякої матриці. Точніше, якщо
\[\{x_{1}, \cdots, x_{m}\} \nonumber\]
є основою для ММ, то ясно, якщо\(x_{j}\) вони поміщені в стовпці матриці називається\(A\) тоді\(\mathbb{R}(A) = M\). Наприклад, якщо\(M\) лінія через,\(\begin{pmatrix} {1}&{1} \end{pmatrix}^{T}\) то
\[P = \begin{pmatrix} {1}\\ {1} \end{pmatrix} \frac{1}{2} \begin{pmatrix} {1}&{1} \end{pmatrix} \nonumber\]
\[P = \frac{1}{2} \begin{pmatrix} {1}&{1}\\ {1}&{1} \end{pmatrix} \nonumber\]
ортогональна проекція на\(M\).
Вправи
Гілберт Странг розтягувався на стійці довжиною\(l = 6, 7, 8\) ноги під прикладеною силою\(f = 1, 2, 4\) тонн. Припускаючи закон Гука\(l−L = cf\), знайдіть його відповідність\(c\), і початкову висоту\(L\), найменшими квадратами.
Що стосується прикладу § 3, зауважте, що через випадкову генерацію шуму, який засмічує переміщення, кожен раз, коли код викликається, кожен раз, коли код викликається.
- Напишіть цикл, який викликає код статистично значущу кількість разів і подайте штрихові графіки середньої жорсткості волокна та його стандартного відхилення для кожного волокна разом із пов'язаним M—файлом.
- Експериментуйте з різними рівнями шуму з метою визначення рівня, вище якого стає важко розрізнити жорстке волокно. Ретельно поясніть свої висновки.
Знайдіть матрицю, яка\(\mathbb{R}^3\) проектує на лінію, яку охоплює\(\begin{pmatrix} {1}&{0}&{1} \end{pmatrix}^{T}\).
Знайдіть матрицю, яка\(\mathbb{R}^3\) проектує на лінію, що охоплює\(\begin{pmatrix} {1}&{0}&{1} \end{pmatrix}^{T}\) і\(\begin{pmatrix} {1}&{1}&{-1} \end{pmatrix}^{T}\).
Якщо\(P\) проекція\(\mathbb{R}^m\) на k — вимірний підпростір\(M\), що таке ранг\(P\) і що таке\(\mathbb{R}(P)\)?
