8.8: Вектори

Цілі навчання

• Подивитися вектори геометрично.
• Знайти величину і напрямок.
• Виконайте додавання векторів і скалярне множення.
• Знайдіть складову форму вектора.
• Знайти вектор одиниці виміру в напрямку$v$.
• Виконуйте операції з векторами в терміні$i$ і$j$.
• Знайдіть крапковий добуток двох векторів.

Літак летить зі швидкістю польоту$200$ миль на годину на чолі на підшипнику SE$140°$. Північний вітер (з півночі на південь) дме зі швидкістю$16.2$ миль на годину, як показано на малюнку$\PageIndex{1}$. Що таке швидкість землі і фактичний підшипник літака?

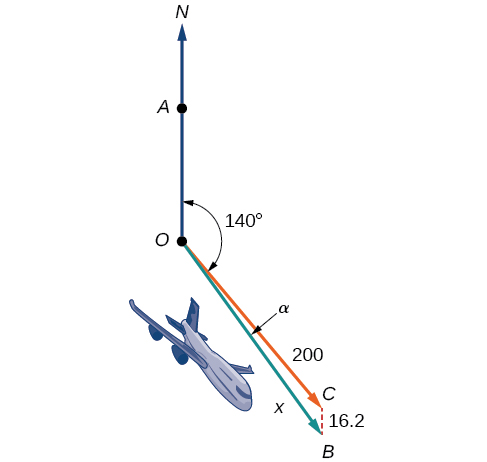
Малюнок$\PageIndex{1}$

Наземна швидкість відноситься до швидкості площини щодо землі. Повітряна швидкість відноситься до швидкості, яку літак може подорожувати щодо навколишньої повітряної маси. Ці дві величини не однакові через вплив вітру. У більш ранньому розділі ми використовували трикутники для вирішення подібної проблеми, пов'язаної з рухом човнів. Пізніше в цьому розділі ми знайдемо швидкість та підшипник літака, досліджуючи інший підхід до проблем такого типу. Однак спочатку давайте розберемо основи векторів.

Геометричний вигляд векторів

Вектор - це певна величина, намальована у вигляді відрізка лінії з наконечником стрілки на одному кінці. Він має початкову точку, де вона починається, і кінцеву точку, де вона закінчується. Вектор визначається його величиною, або довжиною лінії, і її напрямком, позначеного наконечником стрілки в кінцевій точці. Таким чином, вектор - це спрямований відрізок лінії. Існують різні символи, які відрізняють вектори від інших величин:

• Нижній регістр, напівжирний тип, зі стрілкою зверху або без такої $u$, як$w$,$\overrightarrow{v}$,$\overrightarrow{u}$,$\overrightarrow{w}$.
• Враховуючи початкову точку$P$ та$Q$ кінцеву точку, вектор можна представити у вигляді$\overrightarrow{PQ}$. Стрілка зверху - це те, що вказує на те, що це не просто лінія, а спрямований відрізок лінії.
• Враховуючи початкову точку$(0,0)$ та кінцеву точку$(a,b)$, вектор може бути представлений у вигляді$⟨a,b⟩$.

Цей останній символ$⟨a,b⟩$ має особливе значення. Його називають стандартним положенням. Вектор положення має початкову точку$(0,0)$ та кінцеву точку$⟨a,b⟩$. Щоб змінити будь-який вектор на вектор положення, ми думаємо про зміну x -координат і зміну y -координат. Таким чином, якщо початкова точка вектора$\overrightarrow{CD}$ є,$C(x_1,y_1)$ а кінцева точка є$D(x_2,y_2)$, то вектор положення знаходять шляхом обчислення

$$\begin{align*} \overrightarrow{AB} &= ⟨x_2−x_1,y_2−y_1⟩ \\[4pt] &= ⟨a,b⟩ \end{align*}$$

На$\PageIndex{2}$ малюнку ми бачимо вихідний вектор$\overrightarrow{CD}$ і вектор положення$\overrightarrow{AB}$.

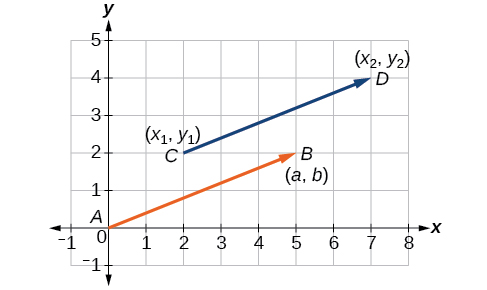
Малюнок$\PageIndex{2}$

ВЛАСТИВОСТІ ВЕКТОРІВ

Вектор - це спрямований відрізок лінії з початковою точкою і кінцевою точкою. Вектори ідентифікуються за величиною, або довжиною лінії, і напрямком, представленим стрілкою, що вказує на кінцеву точку. Вектор положення має початкову точку в$(0,0)$ і ідентифікується його кінцевою точкою$⟨a,b⟩$.

Приклад$\PageIndex{1A}$: Find the Position Vector

Розглянемо вектор, початкова точка якого$P(2,3)$ і кінцева точка є$Q(6,4)$. Знайдіть вектор положення.

Рішення

Вектор положення знаходить шляхом віднімання однієї$x$ -координати від іншої$x$ -координати, а однієї$y$ -координати від іншої$y$ -координати. Таким чином

$$\begin{align*} v &= ⟨6−2,4−3⟩ \\[4pt] &=⟨4,1⟩ \end{align*}$$

Вектор позиції починається з$(0,0)$ і закінчується на$(4,1)$. Графіки обох векторів наведені на малюнку$\PageIndex{3}$.

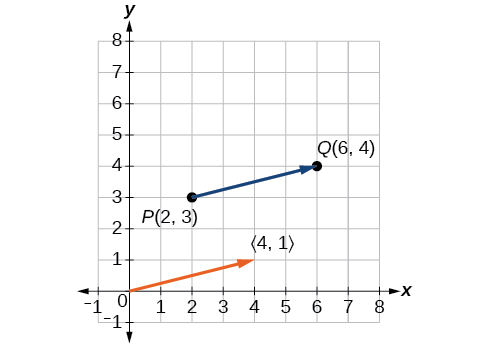
Малюнок$\PageIndex{3}$

Ми бачимо, що вектор положення є$⟨4,1⟩$.

Приклад$\PageIndex{1B}$: Drawing a Vector with the Given Criteria and Its Equivalent Position Vector

Знайдіть вектор положення, враховуючи, що вектор$v$ має початкову точку в$(−3,2)$ і кінцеву точку в$(4,5)$, а потім графік обох векторів в одній площині.

Рішення

Вектор положення знаходить за допомогою наступного розрахунку:

$$\begin{align*} v &= ⟨4−(−3),5−2⟩ \\[4pt] &= ⟨7,3⟩ \end{align*}$$

Таким чином, вектор положення починається в$(0,0)$ і закінчується в$(7,3)$. Див$\PageIndex{4}$. Малюнок.

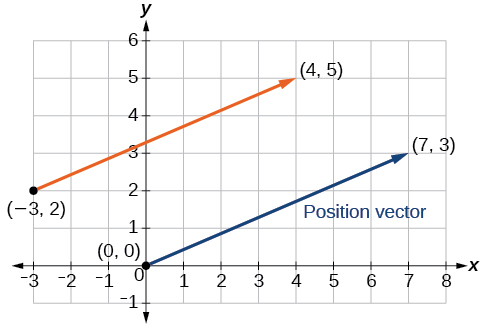
Малюнок$\PageIndex{4}$

Вправа$\PageIndex{1}$

Намалюйте вектор$\vec{v}$, який з'єднується від початку до точки$(3,5)$.

Відповідь

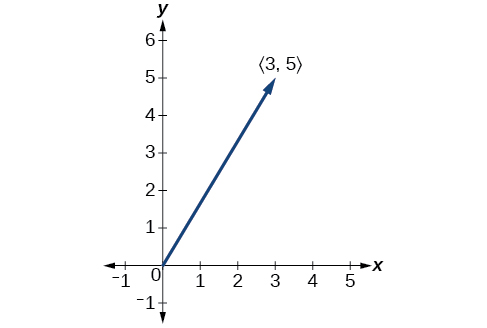
Малюнок$\PageIndex{5}$

Пошук величини та напряму

Для роботи з вектором нам потрібно вміти знаходити його величину і напрямок. Знаходимо його величину за допомогою теореми Піфагора або формули відстані, і знаходимо його напрямок за допомогою оберненої тангенсної функції.

ВЕЛИЧИНА І НАПРЯМОК ВЕКТОРА

За заданим вектором$\vec{v}=⟨a,b⟩$ положення величина знаходить по$| v |=\sqrt{a^2+b^2}$ .Напрямок дорівнює куту, утвореному з$x$ -віссю, або з$y$ -віссю, в залежності від застосування. Для вектора положення напрямок знаходиться за допомогою$\tan \theta=\left(\dfrac{b}{a}\right)⇒\theta={\tan}^{−1}\left(\dfrac{b}{a}\right)$, як показано на малюнку$\PageIndex{6}$.

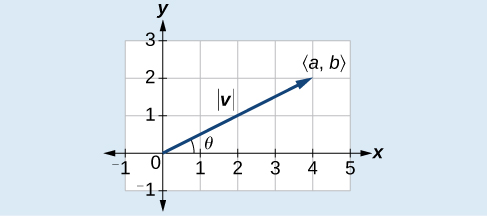
Малюнок$\PageIndex{6}$

Два вектора$\vec{v}$ і$\vec{u}$ вважаються рівними, якщо вони мають однакову величину і однаковий напрямок. Крім того, якщо обидва вектора мають однаковий вектор положення, вони рівні.

Приклад$\PageIndex{2A}$: Finding the Magnitude and Direction of a Vector

Знайдіть величину і напрямок вектора з початковою точкою$P(−8,1)$ і кінцевою$Q(−2,−5)$ точкою.Намалюйте вектор.

Рішення

Спочатку знайдіть вектор положення.

$$\begin{align*} u &= ⟨−2,−(−8),−5−1⟩ \\[4pt] &= ⟨6,−6⟩ \end{align*}$$

Ми використовуємо теорему Піфагора, щоб знайти величину.

$$\begin{align*} |u| &= \sqrt{{(6)}^2+{(−6)}^2} \\[4pt] &= \sqrt{72} \\[4pt] &=\sqrt{62} \end{align*}$$

Напрямок задається як

$$\begin{align*} \tan \theta & =\dfrac{−6}{6}=−1\rightarrow \theta={\tan}^{−1}(−1) \\[4pt] &= −45° \end{align*}$$

Однак кут закінчується в четвертому квадранті, тому ми додаємо,$360°$ щоб отримати позитивний кут. Таким чином,$−45°+360°=315°$. Див$\PageIndex{7}$. Малюнок.

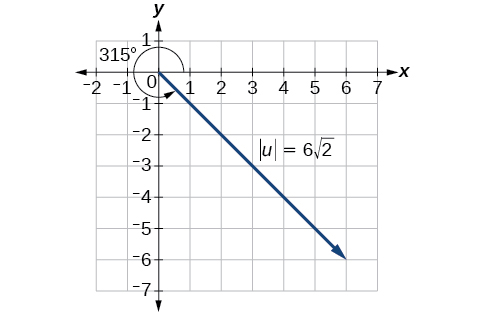
Малюнок$\PageIndex{7}$

Приклад$\PageIndex{2B}$: Showing That Two Vectors Are Equal

Показати, що вектор$\vec{v}$ з початковою точкою в$(5,−3)$ і кінцевою точкою в$(−1,2)$ дорівнює вектору$\vec{u}$ з початковою точкою в$(−1,−3)$ і кінцевою точкою в$(−7,2)$. Намалюйте вектор положення на тій же сітці, що$\vec{v}$ і$\vec{u}$. Далі знайдіть величину і напрямок кожного вектора.

Рішення

Як показано на малюнку$\PageIndex{8}$, намалюйте вектор,$\vec{v}$ починаючи з початкової$(5,−3)$ та кінцевої точки$(−1,2)$. Намалюйте вектор$\vec{u}$ з початковою точкою$(−1,−3)$ та кінцевою точкою$(−7,2)$. Знайдіть стандартну позицію для кожного.

Далі знайдіть і намалюйте вектор положення для$\vec{v}$ і$\vec{u}$. У нас є

$$\begin{align*} v &= ⟨−1−5,2−(−3)⟩ \\[4pt] &= ⟨−6,5⟩u \\[4pt] &= ⟨−7−(−1),2−(−3)⟩ \\[4pt] & =⟨−6,5⟩ \end{align*}$$

Так як вектори положення однакові,$\vec{v}$ і$\vec{u}$ однакові.

Альтернативний спосіб перевірки векторної рівності - показати, що величина і напрямок однакові для обох векторів. Щоб показати, що величини рівні, використовують теорему Піфагора.

$$\begin{align*} |v| &= \sqrt{{(−1−5)}^2+{(2−(−3))}^2} \\[4pt] &= \sqrt{{(−6)}^2+{(5)}^2} \\[4pt] &= \sqrt{36+25} \\[4pt] &= \sqrt{61} \\[4pt] |u| &= \sqrt{{(−7−(−1))}^2+{(2−(−3))}^2} \\[4pt] &=\sqrt{{(−6)}^2+{(5)}^2} \\[4pt] &= \sqrt{36+25} \\[4pt] &= \sqrt{61} \end{align*}$$

Оскільки величини рівні, нам тепер потрібно перевірити напрямок. Використання функції дотичної з вектором положення дає

$$\begin{align*} \tan \theta &= −\dfrac{5}{6}⇒\theta={\tan}^{−1}\left(−\dfrac{5}{6}\right) \\[4pt] & = −39.8° \end{align*}$$

Однак ми бачимо, що вектор позиції закінчується у другому квадранті, тому ми додаємо$180°$. Таким чином, напрямок є$−39.8°+180°=140.2°$.

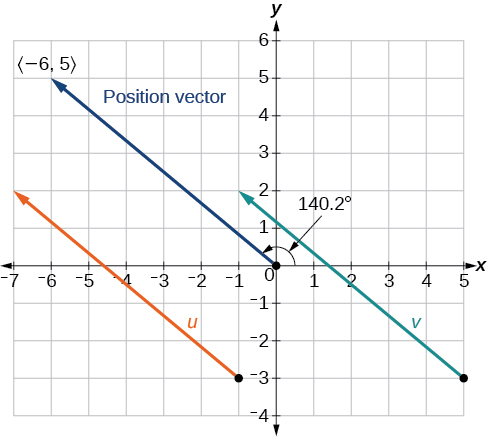
Малюнок$\PageIndex{8}$

Виконання векторного додавання та скалярного множення

Тепер, коли ми розуміємо властивості векторів, ми можемо виконувати операції з їх участю. Хоча зручно думати про вектор$u=⟨x,y⟩$ як стрілку або спрямований відрізок лінії від початку до точки$(x,y)$, вектори можуть бути розташовані в будь-якому місці площини. Сума двох векторів$\vec{u}$ і$\vec{v}$, або векторне додавання, створює третій вектор$\overrightarrow{u+ v}$, результуючий вектор.

Щоб знайти$\overrightarrow{u + v}$, ми спочатку малюємо вектор$\vec{u}$, а з кінцевого кінця$\vec{u}$, ми намалювали вектор$\vec{v}$. Іншими словами, у нас є початкова точка$\vec{v}$ зустрітися кінцевого кінця$\vec{u}$. Ця позиція відповідає поняттю, що ми рухаємося уздовж першого вектора, а потім, від його кінцевої точки, рухаємося по другому вектору. Сума$\overrightarrow{u + v}$ є результуючим вектором, оскільки вона є результатом додавання або віднімання двох векторів. Результуючий вектор рухається безпосередньо від початку$\vec{u}$ до кінця$\vec{v}$ прямим шляхом, як показано на малюнку$\PageIndex{9}$.

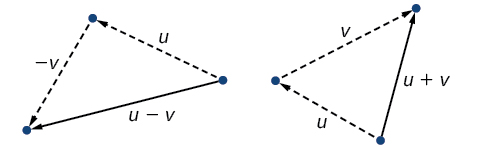
Малюнок$\PageIndex{9}$

Векторне віднімання схоже на додавання векторів. Щоб знайти$\overrightarrow{u − v}$, перегляньте його як$\overrightarrow{u + (−v)}$. Додавання$\overrightarrow{−v}$ - це зворотний напрямок$\vec{v}$ і додавання його до кінця$\vec{u}$. Новий вектор починається на початку$\vec{u}$ і зупиняється в кінцевій точці$\overrightarrow{−v}$. Див. Рисунок$\PageIndex{10}$ для візуального зображення, яке порівнює додавання векторів та віднімання векторів за допомогою паралелограм.

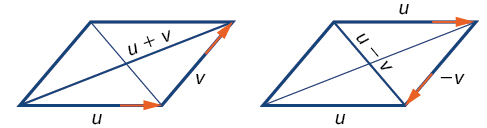
Малюнок$\PageIndex{10}$

Приклад$\PageIndex{3}$: Adding and Subtracting Vectors

Задано$u=⟨3,−2⟩$ і$v=⟨−1,4⟩$, знайдіть два нових вектора$\overrightarrow{u + v}$, і$\overrightarrow{u − v}$.

Рішення

Щоб знайти суму двох векторів, складаємо складові. Таким чином,

$$\begin{align*} u+v &= ⟨3,−2⟩+⟨−1,4⟩ \\[4pt] &= ⟨3+(−1),−2+4⟩ \\[4pt] &=⟨2,2⟩ \end{align*}$$

Див$\PageIndex{11a}$. Малюнок.

Щоб знайти різницю двох векторів, додайте негативні складові$\vec{v}$ to$\vec{u}$. Таким чином,

$$\begin{align*}u+(−v) &=⟨3,−2⟩+⟨1,−4⟩ \\[4pt] &= ⟨3+1,−2+(−4)⟩ \\[4pt] &= ⟨4,−6⟩ \end{align*}$$

Див$\PageIndex{11b}$. Малюнок.

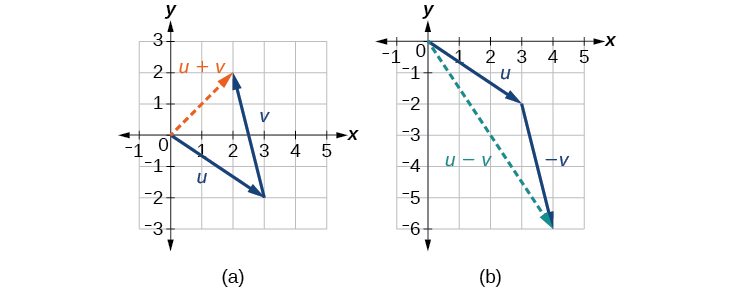
Малюнок$\PageIndex{11}$: (а) Сума двох векторів (b) Різниця двох векторів

Множення на скаляр

У той час як додавання і віднімання векторів дає нам новий вектор з різною величиною і напрямком, процес множення вектора на скаляр, константу, змінює тільки величину вектора або довжину прямої. Скалярне множення не впливає на напрямок, якщо скаляр не є негативним, і в цьому випадку напрямок результуючого вектора протилежний напрямку вихідного вектора.

СКАЛЯРНЕ МНОЖЕННЯ

Скалярне множення передбачає добуток вектора і скаляра. Кожен компонент вектора множиться на скаляр. Таким чином, щоб$v=⟨a,b⟩$ помножити на$k$, ми маємо

$kv=⟨ka,kb⟩$

Змінюється тільки величина,$k$ хіба що негативна, а потім вектор змінює напрямок.

Приклад$\PageIndex{4}$: Performing Scalar Multiplication

Задано вектор $\vec{v}=⟨3,1⟩$$3\vec{v}$, знайти$\dfrac{1}{2}$, і$\vec{−v}$.

Рішення

Див. Рисунок$\PageIndex{12}$ для геометричної інтерпретації. Якщо$\vec{v}=⟨3,1⟩$, то

$$\begin{align*} 3v &= ⟨3⋅3,3⋅1⟩ \\[4pt] &= ⟨9,3⟩ \\[4pt] \dfrac{1}{2}v &= ⟨\dfrac{1}{2}⋅3,\dfrac{1}{2}⋅1⟩ \\[4pt] &=⟨\dfrac{3}{2},\dfrac{1}{2}⟩ \\[4pt] −v &=⟨−3,−1⟩ \end{align*}$$

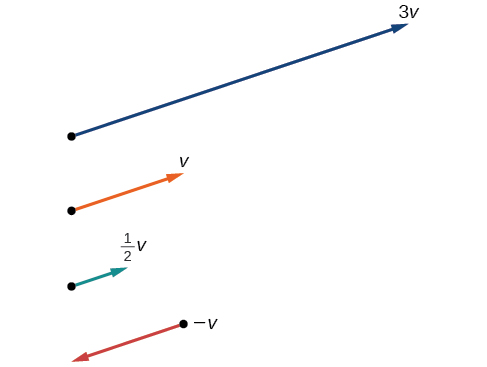
Малюнок$\PageIndex{12}$

Аналіз

Зверніть увагу,$3\vec{v}$ що вектор в три рази більше довжини$\vec{v}$,$\dfrac{1}{2}\vec{v}$ половина довжини$\vec{v}$ і$\overrightarrow{–v}$ є такою ж довжиною$\vec{v}$, але в зворотному напрямку.

Вправа$\PageIndex{2}$

Знайдіть$3u$ задане скалярне кратне$\vec{u}=⟨5,4⟩$.

Відповідь

$3u=⟨15,12⟩$

Приклад$\PageIndex{5}$

Знайдіть лінійне рівняння для вирішення наступних невідомих величин: Одне число перевищує інше число на$17$ і їх сума дорівнює$31$. Знайдіть два числа.

Рішення

По-перше, ми повинні помножити кожен вектор на скаляр.

$$\begin{align*} 3u &= 3⟨3,−2⟩ \\[4pt] &= ⟨9,−6⟩ \\[4pt] 2v &= 2⟨−1,4⟩ \\[4pt] &= ⟨−2,8⟩ \end{align*}$$

Потім складіть два разом.

$$\begin{align*} w &= 3u+2v \\[4pt] &=⟨9,−6⟩+⟨−2,8⟩ \\[4pt] &= ⟨9−2,−6+8⟩ \\[4pt] &= ⟨7,2⟩ \end{align*}$$

Отже,$w=⟨7,2⟩$.

Пошук форми компонента

У деяких додатках, що стосуються векторів, нам корисно мати можливість розбити вектор на його компоненти. Вектори складаються з двох компонентів: горизонтальна складова - це$x$ напрямок, а вертикальна -$y$ напрямок. Наприклад, ми бачимо на графіку на малюнку$\PageIndex{13}$, що вектор положення$⟨2,3⟩$ походить від додавання векторів$v_1$ і$v_2$. Ми маємо$v_2$ з початковою точкою$(0,0)$ та кінцевою точкою$(2,0)$.

$$\begin{align*} v_1 &= ⟨2−0,0−0⟩ \\[4pt] &= ⟨2,0⟩ \end{align*}$$

Ми також маємо$v_2$ з початковою точкою$(0,0)$ та кінцевою точкою$(0, 3)$.

$$\begin{align*} v_2 &= ⟨0−0,3−0⟩ \\[4pt] &= ⟨0,3⟩ \end{align*}$$

Тому вектор положення є

$$\begin{align*} v &= ⟨2+0,3+0⟩ \\[4pt] &= ⟨2,3⟩ \end{align*}$$

Використовуючи теорему Піфагора, величина$v_1$ is$2$, і величина$v_2$ is$3$. Щоб знайти величину$v$, скористайтеся формулою з вектором положення.

$$\begin{align*} |v| &= \sqrt{{|v_1|}^2+{|v_2|}^2} \\[4pt] &= \sqrt{2^2+3^2} \\[4pt] &= \sqrt{13} \end{align*}$$

Величина$v$ є$\sqrt{13}$. Щоб знайти напрямок, скористаємося функцією дотичної$\tan \theta=\dfrac{y}{x}$.

$$\begin{align*} \tan \theta &= \dfrac{v_2}{v_1} \\[4pt] \tan \theta &= \dfrac{3}{2} \\[4pt] \theta &={\tan}^{−1}\left(\dfrac{3}{2}\right)=56.3° \end{align*}$$

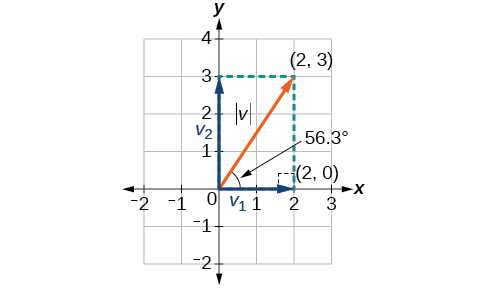
Малюнок$\PageIndex{13}$

Таким чином, величина$\vec{v}$ є$\sqrt{13}$ і напрямок$56.3^{\circ}$ відходить від горизонталі.

Приклад$\PageIndex{6}$: Finding the Components of the Vector

Знайдіть складові вектора $\vec{v}$з початковою точкою$(3,2)$ та кінцевою точкою$(7,4)$.

Рішення

Спочатку знайдіть стандартне положення.

$$\begin{align*} v &= ⟨7−3,4−2⟩ \\[4pt] &= ⟨4,2⟩ \end{align*}$$

Дивіться ілюстрацію на рис$\PageIndex{14}$.

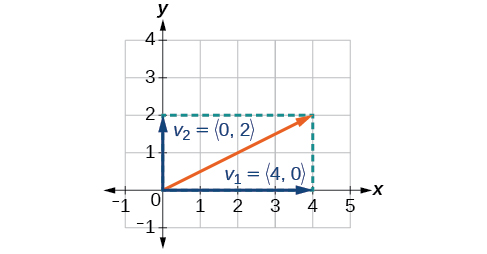
Малюнок$\PageIndex{14}$

Горизонтальна складова є$\vec{v_1}=⟨4,0⟩$ і вертикальна складова$\vec{v_2}=⟨0,2⟩$.

Знаходження вектора одиниці в напрямку$v$

Крім пошуку компонентів вектора, також корисно при вирішенні задач знайти вектор в тому ж напрямку, що і заданий вектор, але величини$1$. Ми називаємо вектор з величиною$1$ одиничного вектора. Потім ми можемо зберегти напрямок вихідного вектора, спрощуючи обчислення.

Одиничні вектори визначаються за складовими. Горизонтальний одиничний вектор записується як$\vec{i}=⟨1,0⟩$ і спрямований вздовж позитивної горизонтальної осі. Вертикальний одиничний вектор записується як$\vec{j}=⟨0,1⟩$ і спрямований вздовж позитивної вертикальної осі. Див$\PageIndex{15}$. Малюнок.

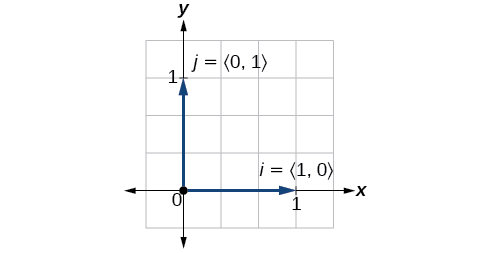
Малюнок$\PageIndex{15}$

ВЕКТОРИ ОДИНИЦІ

Якщо $\vec{v}$є ненульовим вектором, то$\dfrac{v}{| v |}$ є одиничним вектором у напрямку $v$. Будь-який вектор, розділений на його величину, є одиничним вектором. Зверніть увагу, що величина завжди скалярна, а ділення на скаляр - це те саме, що множення на зворотне скаляра.

Приклад$\PageIndex{7}$: Finding the Unit Vector in the Direction of $v$

Знайдіть одиничний вектор в тому ж напрямку, що і$v=⟨−5,12⟩$.

Рішення

Спочатку знайдемо величину.

$$\begin{align*} |v| &= \sqrt{{(−5)}^2+{(12)}^2} \\[4pt] &= \sqrt{25+144} \\[4pt] &=\sqrt{169} \\[4pt] &= 13 \end{align*}$$

Потім ми ділимо кожен компонент на$| v |$, який дає одиничний вектор в тому ж напрямку, що і$\vec{v}$:

$\dfrac{v}{| v |} = −\dfrac{5}{13}i+\dfrac{12}{13}j$

або, у складовій формі

$\dfrac{v}{| v |}= \left \langle -\dfrac{5}{13},\dfrac{12}{13} \right \rangle$

Див$\PageIndex{16}$. Малюнок.

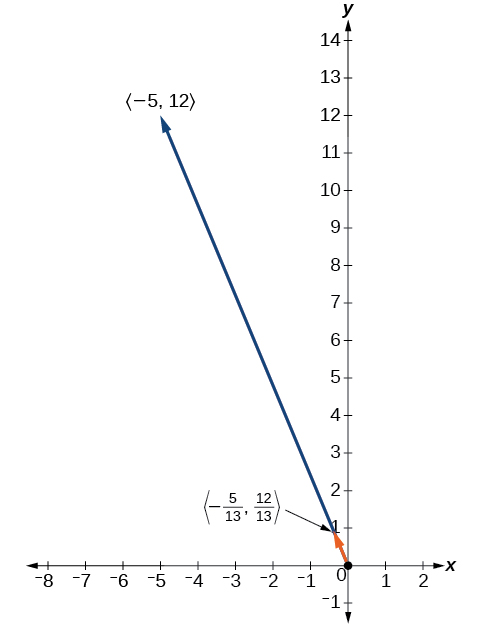
Малюнок$\PageIndex{16}$

Переконайтеся, що величина вектора одиниці дорівнює$1$. Величина$−\dfrac{5}{13}i+\dfrac{12}{13}j$ задається як

$$\begin{align*} \sqrt{ {\left(−\dfrac{5}{13}\right)}^2+{ \left(\dfrac{12}{13}\right) }^2 } &= \sqrt{\dfrac{25}{169}+\dfrac{144}{169}} \\[4pt] &= \sqrt{\dfrac{169}{169}}\\ &=1 \end{align*}$$

Вектор$u=\dfrac{5}{13}i+\dfrac{12}{13}j$ - це одиничний вектор в тому ж напрямку, що і$v=⟨−5,12⟩$.

Виконання операцій з векторами в терміні$i$ і$j$

Поки що ми досліджували основи векторів: величину і напрямок, додавання і віднімання векторів, скалярне множення, складові векторів, геометричне подання векторів. Тепер, коли ми знайомі з загальними стратегіями, які використовуються в роботі з векторами, ми будемо представляти вектори в прямокутних координатах через$i$ і$j$.

ВЕКТОРИ В ПРЯМОКУТНІЙ ПЛОЩИНІ

Задано вектор$\vec{v}$ з початковою точкою$P=(x_1,y_1)$ та кінцевою точкою$Q=(x_2,y_2)$,$\vec{v}$ записується як

$$v=(x_2−x_1)i+(y_1−y_2)j$$

Вектор положення від$(0,0)$ до$(a,b)$, де$(x_2−x_1)=a$ і$(y_2−y_1)=b$, записується як$\vec{v} = \vec{ai}+ \vec{bj}$. Ця векторна сума називається лінійною комбінацією векторів$\vec{i}$ і$\vec{j}$.

Величина$\vec{v} = \overrightarrow{ai} + \overrightarrow{bj}$ задається як$| v |=\sqrt{a^2+b^2}$. Див$\PageIndex{17}$. Малюнок.

Малюнок$\PageIndex{17}$

Приклад$\PageIndex{8A}$: Writing a Vector in Terms of $i$ and $j$

Задано вектор$\vec{v}$ з початковою точкою$P=(2,−6)$ і кінцевою точкою$Q=(−6,6)$, запишіть вектор через$\vec{i}$ і$\vec{j}$.

Рішення

Почніть з написання загальної форми вектора. Потім замініть координати заданими значеннями.

$$\begin{align*} v &= (x_2−x_1)i+(y_2−y_1)j \\[4pt] &=(−6−2)i+(6−(−6))j \\[4pt] &= −8i+12j \end{align*}$$

Приклад$\PageIndex{8B}$: Writing a Vector in Terms of $i$ and $j$ Using Initial and Terminal Points

Задано початкову точку$P_1=(−1,3)$ та$P_2=(2,7)$ кінцеву точку, запишіть вектор$\vec{v}$ через$\vec{i}$ і$\vec{j}$.

Рішення

Почніть з написання загальної форми вектора. Потім замініть координати заданими значеннями.

$$\begin{align*} v &= (x_2−x_1)i+(y_2−y_1)j \\[4pt] v &= (2−(−1))i+(7−3)j \\[4pt] &= 3i+4j \end{align*}$$

Вправа$\PageIndex{3}$

Запишіть вектор$\vec{u}$ з початковою точкою$P=(−1,6)$ та кінцевою точкою$Q=(7,−5)$ через$\vec{i}$ і$\vec{j}$.

Відповідь

$u=8i−11j$

Виконання операцій над векторами в терміні$i$ і$j$

Коли вектори записуються через$i$ і$j$, ми можемо здійснювати додавання, віднімання і скалярне множення, виконуючи операції над відповідними компонентами.

ДОДАВАННЯ ТА ВІДНІМАННЯ ВЕКТОРІВ У ПРЯМОКУТНИХ КООРДИНАТАХ

Дано$v = ai + bj$ і$u = ci + dj$, потім

$$\begin{align*} v+u &= (a+c)i+(b+d)j \\[4pt] v−u &= (a−c)i+(b−d)j \end{align*}$$

Приклад$\PageIndex{9}$: Finding the Sum of the Vectors

Знайти суму$v_1=2i−3j$ і$v_2=4i+5j$.

Рішення

$$\begin{align*} v_1+v_2 &= (2+4)i+(−3+5)j \\[4pt] &= 6i+2j \end{align*}$$

Обчислення складової форми вектора: напрямок

Ми бачили, як малювати вектори відповідно до їх початкової та кінцевої точок та як знайти вектор положення. Ми також розглянули позначення векторів, намальованих конкретно в декартовій координатній площині з використанням$i$ і$j$. Для будь-якого з цих векторів ми можемо обчислити величину. Тепер ми хочемо об'єднати ключові моменти, і дивитися далі на ідеї масштабу і напрямки.

Обчислення напрямку відбувається за тим самим простим процесом, який ми використовували для полярних координат. Знаходимо напрямок вектора, знайшовши кут до горизонталі. Ми робимо це за допомогою базових тригонометричних ідентичностей, але з$| v |$ заміною$r$.

ВЕКТОРНІ КОМПОНЕНТИ ЗА ВЕЛИЧИНОЮ І НАПРЯМКОМ

Враховуючи вектор положення$v=⟨x,y⟩$ та кут напряму$\theta$,

$$\begin{align*} \cos \theta &= \dfrac{x}{|v|} \text{ and } \sin \theta=y|v| \\[4pt] x &= |v| \cos \theta \\[4pt] y &= |v| \sin \theta \end{align*}$$

Таким чином$v=xi+yj=| v | \cos \theta i+| v | \sin \theta j$, і величина виражається як$| v |=\sqrt{x^2+y^2}$.

Приклад$\PageIndex{10}$: Writing a Vector in Terms of Magnitude and Direction

Запишіть вектор довжиною$7$ під кутом$135°$ до позитивної осі x через величину і напрямок.

Рішення

Використовуючи формули перетворення$x=| v | \cos \theta i$ і$y=| v | \sin \theta j$, ми знаходимо, що

$$\begin{align*} x &= 7\cos(135°)i \\[4pt] &= −\dfrac{7\sqrt{2}}{2} \\[4pt] y &=7 \sin(135°)j \\[4pt] &= \dfrac{7\sqrt{2}}{2} \end{align*}$$

Цей вектор може бути записаний як$v=7\cos(135°)i+7\sin(135°)j$ або спрощений як

$v=−\dfrac{7\sqrt{2}}{2}i+\dfrac{7\sqrt{2}}{2}j$

Вправа$\PageIndex{4}$

Вектор рухається від початку до точки$(3,5)$. Запишіть вектор через величину і напрямок.

Відповідь

$v=\sqrt{34}\cos(59°)i+\sqrt{34}\sin(59°)j$

Величина =$34$

$\theta={\tan}^{−1}\left(\dfrac{5}{3}\right)=59.04°$

Пошук точкового добутку двох векторів

Як ми обговорювали раніше в розділі, скалярне множення передбачає множення вектора на скаляр, а результат - вектор. Як ми бачили, множення вектора на число називається скалярним множенням. Якщо помножити вектор на вектор, є дві можливості: точковий добуток і перехресний добуток. Ми розглянемо лише крапковий добуток тут; ви можете зіткнутися з перехресним продуктом у більш просунутих курсах математики.

Точковий добуток двох векторів передбачає множення двох векторів разом, і результат - скаляр.

ДОБУТ DOT

Точковий добуток двох векторів$v=⟨a,b⟩$ і$u=⟨c,d⟩$ є сумою добутку горизонтальних складових і добутку вертикальних складових.

$$v⋅u=ac+bd$$

Щоб знайти кут між двома векторами, скористайтеся формулою нижче.

$$\cos \theta=\dfrac{v}{| v |}⋅\dfrac{u}{| u |}$$

Приклад$\PageIndex{11A}$: Finding the Dot Product of Two Vectors

Знайдіть точковий добуток$v=⟨5,12⟩$ і$u=⟨−3,4⟩$.

Рішення

Використовуючи формулу, ми маємо

$$\begin{align*} v⋅u &= ⟨5,12⟩⋅⟨−3,4⟩ \\[4pt] &= 5⋅(−3)+12⋅4 \\[4pt] &= −15+48 \\[4pt] &= 33 \end{align*}$$

Приклад$\PageIndex{11B}$: Finding the Dot Product of Two Vectors and the Angle between Them

Знайдіть точковий добуток$v_1 = 5i + 2j$ і$v_2 = 3i + 7j$. Потім знайдіть кут між двома векторами.

Рішення

Знайшовши точковий добуток, множимо відповідні складові.

$$\begin{align*} v_1⋅v_2 &= ⟨5,2⟩⋅⟨3,7⟩ \\[4pt] &= 5⋅3+2⋅7 \\[4pt] &= 15+14 \\[4pt] &= 29 \end{align*}$$

Щоб знайти кут між ними, скористаємося формулою$\cos \theta=\dfrac{v}{|v|}⋅\dfrac{u}{|u|}$.

$$\begin{align*} \dfrac{v}{|v|}\cdot \dfrac{u}{|u|} &= \left \langle \dfrac{5}{\sqrt{29}}+\dfrac{2}{\sqrt{29}} \right \rangle \cdot \left \langle \dfrac{3}{\sqrt{58}}+\dfrac{7}{\sqrt{58}} \right \rangle \\[4pt] &=\dfrac{5}{\sqrt{29}}\cdot \dfrac{3}{\sqrt{58}}+\dfrac{2}{\sqrt{29}}\cdot \dfrac{7}{\sqrt{58}} \\[4pt] &= \dfrac{15}{\sqrt{1682}}+\dfrac{14}{\sqrt{1682}}\\ &=\dfrac{29}{\sqrt{1682}} \\[4pt] &= 0.707107 \\[4pt] {\cos}^{-1}(0.707107) &= 45° \end{align*}$$

Див$\PageIndex{18}$. Малюнок.

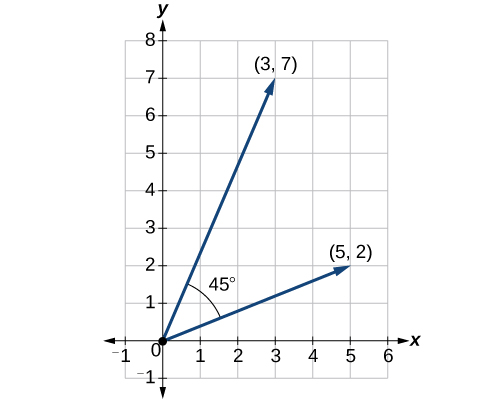
Малюнок$\PageIndex{18}$

Приклад$\PageIndex{11C}$: Finding the Angle between Two Vectors

Знайти кут між$u=⟨−3,4⟩$ і$v=⟨5,12⟩$.

Рішення

Використовуючи формулу, ми маємо

$$\begin{align*} \theta &= {\cos}^{−1}\left(\dfrac{u}{|u|}⋅\dfrac{v}{|v|}\right) \\[4pt] \left(\dfrac{u}{|u|}⋅\dfrac{v}{|v|}\right) &= \dfrac{−3i+4j}{5}⋅\dfrac{5i+12j}{13} \\[4pt] &= \left(− \dfrac{3}{5}⋅ \dfrac{5}{13}\right)+\left(\dfrac{4}{5}⋅ \dfrac{12}{13}\right) \\[4pt] &= −\dfrac{15}{65}+\dfrac{48}{65} \\[4pt] &= \dfrac{33}{65} \\[4pt] \theta &= {\cos}^{−1}\left(\dfrac{33}{65}\right) \\[4pt] &= 59.5^{\circ} \end{align*}$$

Див$\PageIndex{19}$. Малюнок.

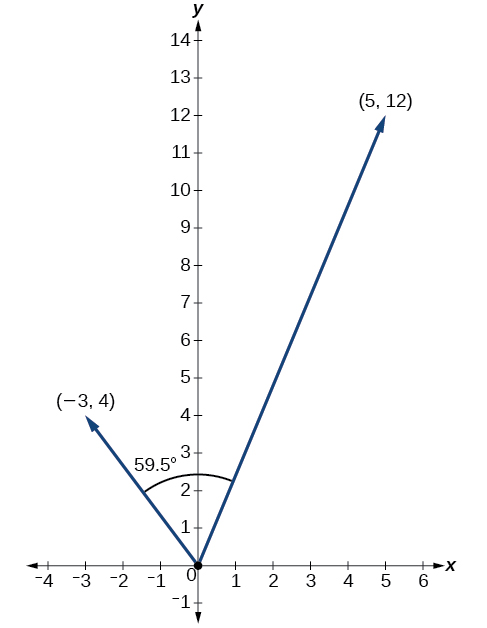
Малюнок$\PageIndex{19}$

Приклад$\PageIndex{11D}$: Finding Ground Speed and Bearing Using Vectors

Тепер у нас є інструменти для вирішення проблеми, яку ми представили при відкритті розділу.

Літак летить зі швидкістю польоту$200$ миль на годину на чолі на підшипнику SE$140°$. Північний вітер (з півночі на південь) дме зі швидкістю$16.2$ миль на годину. Що таке швидкість землі і фактичний підшипник літака? Див$\PageIndex{20}$. Малюнок.

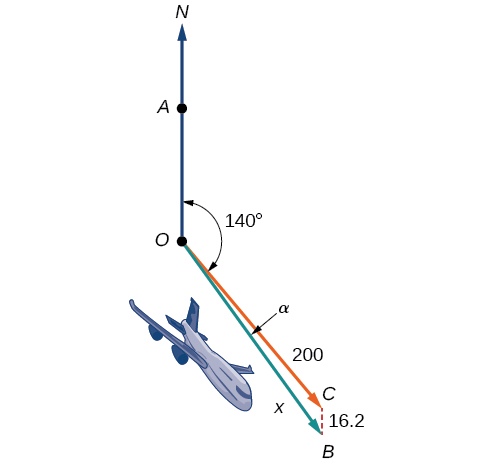
Малюнок$\PageIndex{20}$

Рішення

Швидкість заземлення представлена$x$ на схемі, і нам потрібно знайти кут,$\alpha$ щоб розрахувати відрегульований підшипник, який буде$140°+\alpha$.

Зверніть увагу на малюнку$\PageIndex{20}$, що кут$\angle BCO$ повинен дорівнювати куту$\angle AOC$ за правилом чергування внутрішніх кутів, тому кут$\angle BCO$ дорівнює 140°. Ми можемо знайти$x$ за законом косинусів:

$$\begin{align*} x^2 &= {(16.2)}^2+{(200)}^2−2(16.2)(200) \cos(140°) \\[4pt] x^2 &= 45,226.41 \\[4pt] x &= \sqrt{45,226.41} \\[4pt] x &= 212.7 \end{align*}$$

Наземна швидкість становить приблизно$213$ милі на годину. Тепер ми можемо обчислити підшипник, використовуючи Закон Синеса.

$$\begin{align*} \dfrac{\sin \alpha}{16.2} &= \dfrac{\sin(140°)}{212.7} \\[4pt] \sin \alpha &= \dfrac{16.2 \sin(140°)}{212.7} \\[4pt] &=0.04896 \\[4pt] {\sin}^{−1}(0.04896) &= 2.8° \end{align*}$$

Тому площина має підшипник SE$140°+2.8°=142.8°$. Наземна швидкість -$212.7$ милі на годину.

Медіа: Отримайте доступ до цих онлайн-ресурсів для додаткових інструкцій та практики з векторами.

• Вступ до векторів
• Векторні операції
• Вектор одиниці

Ключові концепції

• Вектор положення має свою початкову точку в початковій точці. Див$\PageIndex{1}$. Приклад.
• Якщо вектор положення однаковий для двох векторів, вони рівні. Див$\PageIndex{2}$. Приклад.
• Вектори визначаються їх величиною і напрямком. Див$\PageIndex{3}$. Приклад.
• Якщо два вектора мають однакову величину і напрямок, вони рівні. Див$\PageIndex{4}$. Приклад.
• Додавання та віднімання векторів призводять до нового вектора, знайденого шляхом додавання або віднімання відповідних елементів. Див$\PageIndex{5}$. Приклад.
• Скалярне множення - це множення вектора на константу. Змінюється лише величина; напрямок залишається незмінним. Див. Приклад$\PageIndex{6}$ і Приклад$\PageIndex{7}$.
• Вектори складаються з двох компонентів: горизонтальної складової вздовж позитивної$x$ осі та вертикальної складової вздовж позитивної$y$ -осі. Див$\PageIndex{8}$. Приклад.
• Одиничний вектор в тому ж напрямку будь-якого ненульового вектора знаходить діленням вектора на його величину.
• Величина вектора в прямокутній системі координат дорівнює$| v |=\sqrt{a^2+b^2}$. Див$\PageIndex{9}$. Приклад.
• У прямокутній системі координат одиничні вектори можуть бути представлені через$ii$ і$jj$ де$i$ представляє горизонтальну складову і$j$ представляє вертикальну складову. Потім,$v = ai + bj$ є скалярним кратним$v$ дійсними числами$a$ і$b$. Див. Приклад$\PageIndex{10}$ і Приклад$\PageIndex{11}$.
• Додавання і віднімання векторів через$i$ і$j$ складається з додавання або віднімання відповідних коефіцієнтів$i$ і відповідних коефіцієнтів$j$. Див$\PageIndex{12}$. Приклад.
• Вектор$v = ai + bj$ записується через величину і напрямок як$v=| v |\cos \theta i+| v |\sin \theta j$. Див$\PageIndex{13}$. Приклад.
• Точковий добуток двох векторів - добуток$i$ термінів плюс добуток$j$ термінів. Див$\PageIndex{14}$. Приклад.
• Ми можемо використовувати точковий добуток, щоб знайти кут між двома векторами. Приклад$\PageIndex{15}$ і приклад$\PageIndex{16}$.
• Точкові продукти корисні для багатьох типів додатків фізики. Див$\PageIndex{17}$. Приклад.

Автори та атрибуція

• Template:ContribOpenStaxPreCalc