Skip to main content
LibreTexts - Ukrayinska

8.1: Арифметичні послідовності

  1. Last updated
  2. Save as PDF
  • Page ID
    59551

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Наступна послідовність чисел має шаблон, який ви зобов'язані розпізнати:

    \(2, 4, 6, 8, 10, 12, 14, 16, 18, …\)

    Швидше за все, ви б описували послідовність словами: послідовність парних чисел. Як варіант, чи можемо ми описати послідовність математично? Тобто, чи можна описати закономірність послідовності парних чисел за допомогою формули? Абсолютно! У цьому розділі будуть розглянуті арифметичні послідовності, способи їх ідентифікації, математично описати їх терміни та зв'язок між арифметичними послідовностями та лінійними функціями. Давайте приступимо!

    Визначення: Послідовність

    Послідовність - це список чисел:\(a_1 , a_2, a_3, a_4 , … , a_n, … \) Послідовність може бути кінцевим або нескінченним списком. Ми\(a_1\) називаємо перший термін,\(a_2\) другий термін, і\(a_n\) «загальний термін» або\(n^{\text{th}}\) термін. Послідовності мають візерунок. Опишемо закономірність в загальному терміні\(a_n\).

    Для послідовності парних чисел:\(2, 4, 6, 8, 10, …\) загальний термін\(a_n = 2n\).

    clipboard_eddc57d00c36a2fbed49c43f696c7302b.png

    Загальний термін\(a_n\) послідовності - це просто функція\(n\), зазначена вище як\(f(n)\), де\(n\) натуральне число (або ціле число, якщо\(n\) починається з нуля).

    Приклад Template:index

    У послідовності парних чисел, що таке\(20^{\text{th}}\) термін в послідовності?

    Рішення

    Загальним терміном послідовності парних чисел є\(a_n = 2n\). Так як\(n =\) термін номер, нас просять знайти\(a_{20}\).

    \(\begin{array}&& a_{20} = 2(20) = 40 &\text{Plug in the term-number \(n=20\)у формулу\(a_n=2n\)}\ end {масив}\)

    Відповідь.\(20^{\text{th}}\) Термін послідовності парних чисел - це число\(40\).

    Визначення: Арифметична послідовність

    Якщо послідовність:\(a_1, a_2, a_3, a_4 , … , a_{n−1}, a_n, …\) виставляє візерунок такий, що

    \[a_n − a_{n−1} = d\]

    Для всіх\(n\) тоді\(d\) дійсне число називається загальною різницею, а послідовність - арифметичною послідовністю.

    Приклад Template:index

    Задано послідовність. Якщо послідовність є арифметичною послідовністю, дайте загальну різницю. Якщо послідовність не є арифметичною послідовністю, поясніть, як вона не може бути арифметичною.

    1. \(25, 32, 39, 46, 53, 60, …\)
    2. \(2, 4, 8, 16, 32, …\)
    3. \(3^2 , 3^4, 3^6, 3^8, 3^{10}, …\)
    4. \(0, 1, 0, 1, 0, 1, …\)

    Рішення

    1. Чи є послідовність

    \(25, 32, 39, 46, 53, 60, … \)

    арифметична послідовність?

    \(\begin{array} &a_2 − a_1 &= 32 − 25 &= \textcolor{red}{7} \\ a_3 − a_2 &= 39 − 32 &= \textcolor{red}{7} \\a_4 − a_3 &= 46 − 39 &= \textcolor{red}{7} \\a_5 − a_4 &= 53 − 46 &= \textcolor{red}{7} \\a_6 − a_5 &= 60 − 53 &= \textcolor{red}{7} \end{array}\)

    Послідовність арифметична і загальна різниця є\(7\).

    1. Чи є послідовність

    \(2, 4, 8, 16, 32, …\)

    арифметична послідовність?

    \(\begin{array} &a_2 − a_1 &= 4 − 2 &= \textcolor{red}{2} \\ a_3 − a_2 &= 8 − 4 &= \textcolor{red}{4} \\a_4 − a_3 &= 16 − 8 &= \textcolor{red}{8} \\a_5 − a_4 &= 32 − 16 &= \textcolor{red}{16} \\ &&\textcolor{red}{2 \neq 4 \neq 8 \neq 16} \end{array}\)

    Послідовність не є арифметичною. \(a_n − a_{n-1}\)не поступається спільної різниці.

    1. Чи є послідовність

    \(3^2 , 3^4, 3^6, 3^8, 3^{10}, …\)

    арифметична послідовність?

    \(\begin{array} &3^4 − 3^2 &= 3^2 (3^2 − 1) &= 9 \cdot 8 &= \textcolor{red}{72} \\ 3^6 − 3^4 &= 3^4 (3^2 − 1) &= 81 \cdot 8 &= \textcolor{red}{648} \end{array}\)

    Так як\(a_3 − a_2 \neq a_2 − a_1\), ми робимо висновок послідовність не арифметична.

    1. Чи є послідовність

    \(0, 1, 0, 1, 0, 1, …\)

    арифметична послідовність?

    \(\begin{array} 1-0 &= \textcolor{red}{1} \\ 0-1 &= \textcolor{red}{-1} \end{array}\)

    Так як\(a_3 − a_2 \neq a_2 − a_1\), послідовність не є арифметичною.

    Знайти загальний член арифметичної послідовності

    Якщо послідовність є арифметичною, загальний термін\(a_n\) визначається за допомогою загальної різниці послідовності.\(d\) Функції форми\(y = mx+b\), відомі як лінійні функції, мають міцний зв'язок з арифметичними послідовностями. Нахил\(m\) лінійної функції еквівалентний загальній різниці\(d\) арифметичної послідовності. Давайте порівняємо арифметичні послідовності з лінійними функціями для побудови\(a_n\), загальним терміном арифметичної послідовності.

    Приклад Template:index

    Знайдіть загальний термін кожної\(a_n\) арифметичної послідовності:

    1. \(4, 7, 10, 13, 16, …\)
    2. \(100, 80, 60, 40, 20, …\)

    Рішення

    Ми створимо таблицю значень для кожної послідовності. У першій колонці буде номер терміну\(n\), починаючи з\(n = 1\). У другому стовпці будуть перераховані терміни послідовності. Загальна відмінність показана збоку другого стовпчика.

    1. Послідовність\(4, 7, 10, 13, 16, …\) має загальну різницю\(d = 3\). Але це також нахил\(m\) лінійної функції\(f(x) = mx + b\).

    \[m = \dfrac{\delta y}{\delta x} = \dfrac{a_n − a_{n-1}}{n − (n − 1))} = \dfrac{d}{1} = d\]

    clipboard_ecbb8d4cf8b9fa5856cc56124c921e2e0.png

    Наведена вище таблиця по суті імітує будь-яку лінійну функцію,\(f(x) = mx+b\).

    • Замість\(x\) послідовності використовують\(n\) −values.
    • Замість\(m =\) нахилу в лінійних функціях послідовності використовують\(d =\) загальну різницю.
    • Замість того\(b\), послідовність позначає одне і те ж значення з\(a_0\).

    Якщо\(a_1\) позначає перший член послідовності, то загальним терміном послідовності є:

    \[a_n = f(n) = d \cdot n + a_0\]

    Щоб знайти загальний термін\(a_n\), нам потрібно буде знайти значення\(a_0\). Існує кілька способів зробити це, але, мабуть, найпростіший - створити додатковий ряд де\(n = 0\), а потім використовувати загальну різницю, щоб знайти\(a_0\). Загальна схема відмінності зберігається і\(a_0 + d = a_1\).

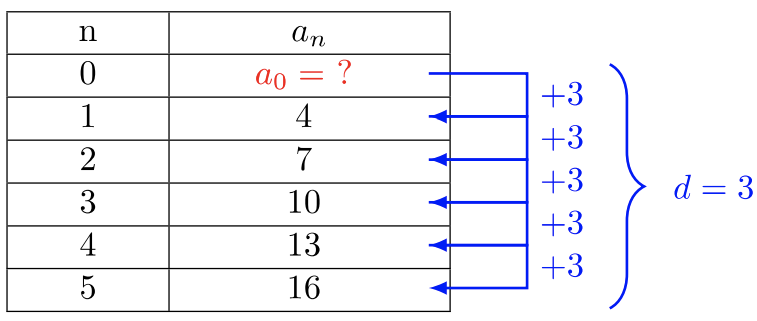
    clipboard_e6eccaea315b268044364f34c0948747d.png

    Знайдіть значення\(a_0\):

    \(\begin{array} &&a_0 + 3 &= 4 \\&a_0 + 3 − 3 &= 4 − 3 \\&a_0 &= 1\end{array}\)

    Загальним терміном послідовності є:

    \(a_n = 3n + 1\)

    1. Використовуйте ту саму стратегію для Прикладу\(8.1.3\) a для вирішення Приклад\(8.1.3\) b Створіть таблицю\(d\), знайдіть загальну різницю та знайдіть\(a_0\) термін послідовності\(100, 80, 60, 40, 20, …\)

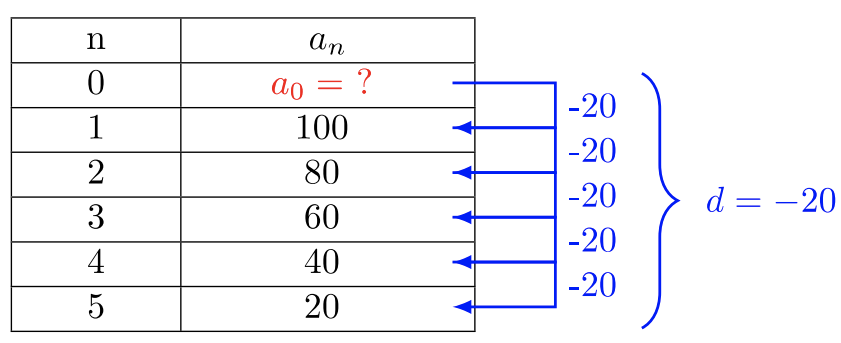
    clipboard_ee68ed069e37b2760f8fc0f27b5a37f04.png

    Загальна відмінність\(d = −20\). Знайдіть значення\(a_0\).

    \(\begin{array} &&a_0 − 20 &= 100 \\ &a_0 − 20 + 20 &= 100 + 20 \\ &a_0 &= 120 \end{array}\)

    Загальним терміном послідовності є:

    \(a_n = −20n + 120\)

    Спробуйте! (Вправи)

    Для #1 -5 задано загальний термін послідовності.

    • \(5\)Перерахуйте перші терміни послідовності:\(a_1, a_2, a_3, a_4, a_5\).
    • Послідовність арифметична?
    1. \(a_n = n^2\)
    2. \(a_n = 4 − 5n\)
    3. \(a_n = 2^n\)
    4. \(a_n = \dfrac{1}{2}n\)
    5. \(a_n = 0.3n + 1\)

    Для #6 -9 наведено таблицю значень. Створіть загальний термін\(a_n\) арифметичної послідовності.

    1. \(n\) \(a_n\)
      \ (n\) ">\(1\) \ (a_n\) ">\(9\)
      \ (n\) ">\(2\) \ (a_n\) ">\(15\)
      \ (n\) ">\(3\) \ (a_n\) ">\(21\)
      \ (n\) ">\(4\) \ (a_n\) ">\(25\)
    1. \(n\) \(a_n\)
      \ (n\) ">\(1\) \ (a_n\) ">\(42\)
      \ (n\) ">\(2\) \ (a_n\) ">\(38\)
      \ (n\) ">\(3\) \ (a_n\) ">\(34\)
      \ (n\) ">\(4\) \ (a_n\) ">\(30\)
    1. \(n\) \(a_n\)
      \ (n\) ">\(1\) \ (a_n\) ">\(7\)
      \ (n\) ">\(2\) \ (a_n\) ">\(7.25\)
      \ (n\) ">\(3\) \ (a_n\) ">\(7.5\)
      \ (n\) ">\(4\) \ (a_n\) ">\(7.75\)
    1. \(n\) \(a_n\)
      \ (n\) ">\(1\) \ (a_n\) ">\(65.4\)
      \ (n\) ">\(2\) \ (a_n\) ">\(52.2\)
      \ (n\) ">\(3\) \ (a_n\) ">\(39\)
      \ (n\) ">\(4\) \ (a_n\) ">\(25.8\)

    Для #10 -15 знайдіть загальний термін арифметичної послідовності. Припустимо, що перший термін є\(a_1\).

    1. \(8, 15, 22, 29, …\)
    2. \(110, 85, 60, 35, …\)
    3. \(9, 7.4, 5.8, 4.2, …\)
    4. \(\dfrac{17}{2} , 8, \dfrac{15}{2} , 7, …\)
    5. \(−20, −8, 4, 16, 28, …\)
    6. \(4 \dfrac{1}{2} , 5 \dfrac{1}{4} , 6, 6 \dfrac{3}{4} , …\)

    Для #16 -20 описано арифметичну послідовність. Знайдіть загальний термін\(a_n\).

    1. Арифметична послідовність має загальну різницю\(d=8\). Перший термін\(a_1 = 28\).
    2. Арифметична послідовність має перший член\(a_1 = 40\) і другий член\(a_2 = 36\).
    3. Арифметична послідовність має перший член\(a_1 = 6\) і третій член\(a_3 = 24\).
    4. Арифметична послідовність має спільну різницю\(d = −2\) і третій член\(a_3 = 15\).
    5. Арифметична послідовність має спільну різницю\(d = 3.6\) і п'ятий член\(a_5 = 10.2\).
    1. Поясніть, як формула загального члена, наведеного в цьому розділі:\(a_n = d \cdot n + a_0\) еквівалентна наступній формулі:\(a_n = a_1 + d(n − 1)\)
    2. Деякі послідовності мають кінцеву кількість членів. Знайдіть кількість членів у скінченній арифметичній послідовності:\(3, 17, 31, … ,143\)
    3. Деякі послідовності мають кінцеву кількість членів. Знайдіть кількість членів у скінченній арифметичній послідовності:\(80, 69, 58, … , −52\)
    4. Створіть формулу для знаходження кількості членів скінченної арифметичної послідовності, якщо задано перший і останній член послідовності. Припустимо, що перший термін є,\(a_1\) а останній термін є\(a_k\).