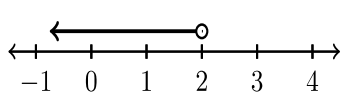
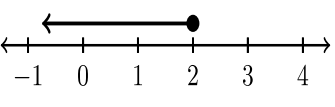
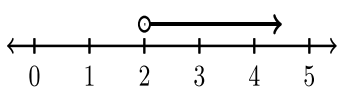
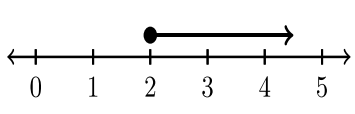
4.2: Інтервальні позначення

Last updated

Oct 27, 2022
Save as PDF
- 4.1: Графіки числових рядків
- 4.3: Розв'язування лінійних нерівностей

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Нерівності нарізають і кубики дійсної числової лінії на сегменти, що представляють інтерес або інтервали. Інтервал - це безперервна, безперервна підмножина дійсних чисел. Як ми можемо відмітити інтервали з простотою? У таблиці нижче наведено інтервальне позначення.

Нерівність	Асоційоване коло	Пов'язані закриття кінцевих точок
Або $<$ або $>$	$clipboard_ea43aad3358d129021fdca988a4b93451.png$	Ліва дужка: (або права дужка:)
Або $≤$ або $≥$	$clipboard_e2e4cf904d07dc1241b9e2632c37e681a.png$	Ліва квадратна дужка: [або права квадратна дужка:]

Нерівності мають $4$ можливі інтервальні замикання:

$(A,B)$	$(A,B]$	$[A,B)$	$[A,B]$
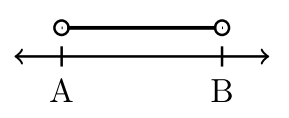
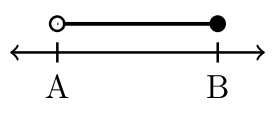
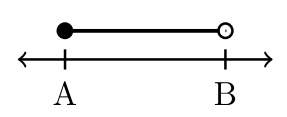
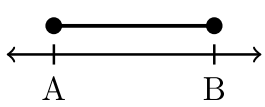
$clipboard_ef4d418cfbf59895619f0546ad98eaf4f.png$	$clipboard_e510d65b9070b6f966181489fb9235b67.png$	$clipboard_edce393fed1ea667df1f70b28c7dbb00e.png$	$clipboard_e9bbd934e732ad52963b83f2dac9d6bed.png$

Найменше число в інтервалі $A$ , завжди вказується першим. Ставляється кома. Найбільше число в інтервалі $B$ ,, вказується після коми. Відповідне закриття розглядається для кожного значення $A$ і $B$ .

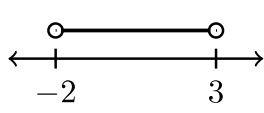
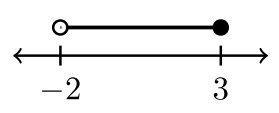
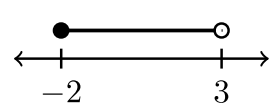
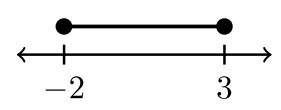
Чотири приклади інтервальних позначень

$−2 < x < 3$	$−2 < x ≤ 3$	$– 2 ≤ x < 3$	$– 2 ≤ x ≤ 3$
$clipboard_eb02fe1b987d2d7aeb60c8fea96ed2803.png$	$clipboard_e019534632b13aa8f1cc8d1d9d3d569d9.png$	$clipboard_edea90ab320a9712b9de1bd8371585e1b.png$	$clipboard_e8b9543e4ca42fb42ac9e7d44a55396c3.png$
$(−2, 3)$	$(−2, 3]$	$[−2, 3)$	$[−2, 3]$

Нескінченності

Існує дві нескінченності: позитивна і негативна. Кожен визначає напрямок на числовій лінії:

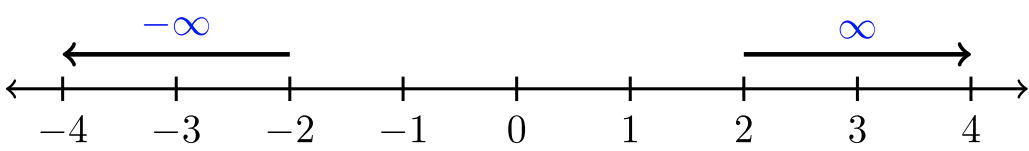
$clipboard_e5b29aa7ac89e2b9ce0b9a83ff14aa23a.png$

Нескінченність не є дійсним числом. Він вказує напрямок. Тому при використанні інтервальних позначень завжди підкладайте $∞$ і $−∞$ з дужками. Ми ніколи не підкладаємо нескінченності квадратною дужкою.

У таблиці нижче наведено чотири приклади інтервальних позначень, які вимагають використання нескінченності.

$x < 2$	$x ≤ 2$	$x > 2$	$x ≥ 2$
$clipboard_e5734c942cda8d2c4a2fc66d380d43045.png$	$clipboard_e02fd4cce2c4fdbda973bec7ec7cea27d.png$	$clipboard_eaf1970b524b0ed982616d4f351aef523.png$	$clipboard_ed53713ef79ac5f76e978d135bba630af.png$
$(−∞, 2)$	$(−∞, 2]$	$(2, ∞)$	$[2, ∞)$

комбінації інтервалів

Якщо два або більше інтервалів перериваються з проміжком у числовому рядку, для зшивання інтервалів між собою символічно використовуються встановлені позначення. Символ, який ми використовуємо для об'єднання інтервалів, є символом об'єднання: $∪$ . У таблиці нижче наведено чотири приклади:

Інтервальні позначення	Графік
$(−∞, −2) ∪ [1, ∞)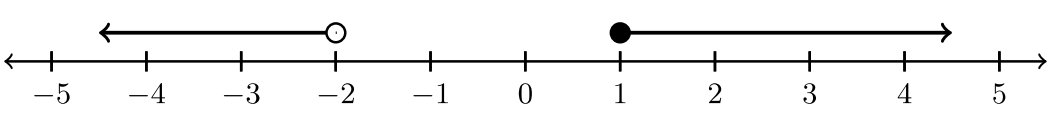$	$clipboard_ee59da9758674b8fbf6ec2276685e5423.png$
$(−∞, −1) ∪ (−1, ∞)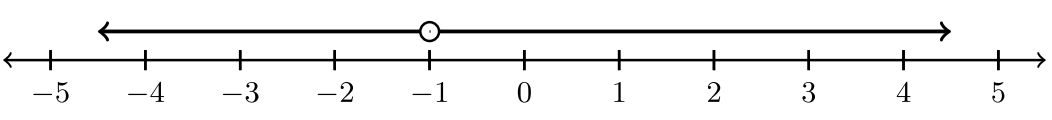$	$clipboard_ed827350d30be0e842f3deae80c6892f7.png$
$\left(−\dfrac{3 \pi}{2} , −\dfrac{\pi}{2} \right) ∪ \left( \dfrac{\pi}{2}, \dfrac{3 \pi}{2} \right)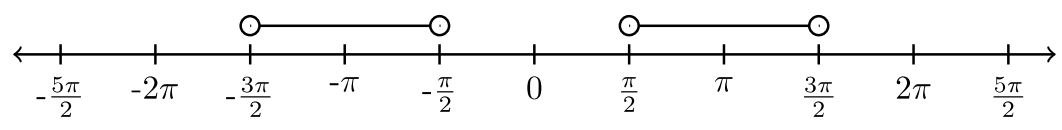$	$clipboard_ebbcf3adffba82a210520564b5a4782e1.png$
$\left[−2 \pi, − \dfrac{\pi}{2} \right) ∪ \left[ \dfrac{3 \pi}{2} , ∞ \right)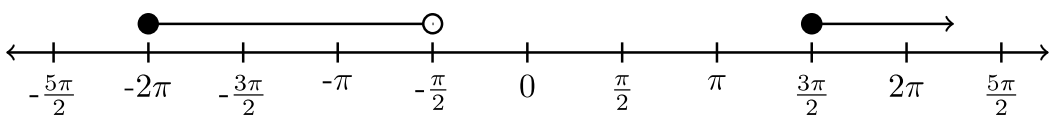$	$clipboard_ef225c28a7a5773a54ade751969064732.png$

Складні нерівності

Інтервали, які мають прогалини, як і показані вище, переводяться в складні нерівності. Реальні рішення належать в тому чи іншому інтервалі. Слово «або» грає ключову роль при перекладі. Наприклад: інтервал $(−∞, −2) ∪ [1, ∞)$ перекладається на пов'язану з ним складну нерівність:

$x < -2$ або $x ≥ 1$

Слово «і» не може бути використано між нерівностями, оскільки число не може належати обом інтервалам одночасно. Наприклад, $x = 5$ це рішення, оскільки $5$ належить до інтервалу $x ≥ 1$ , але $5$ не належить до інтервалу $x < −2$ . Проте через слова «або» $x = 5$ є рішенням інтервалу $(−∞, −2) ∪ [1, ∞)$ .

Спробуйте! (Вправи)

Для вправ #1 -6 встановіть нерівність та інтервальні позначення, пов'язані з графіком.

Графік			Нерівність	Інтервальні позначення
$clipboard_e141ee93db0e0b1fcece04011d50b027c.png$
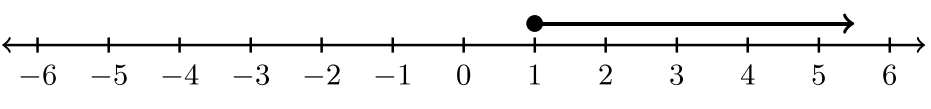$clipboard_ee998ec64608d5197c3eb0225a8dabfb4.png$
$clipboard_e387a79a4c9d9a3c5536f90ca06cc706a.png$
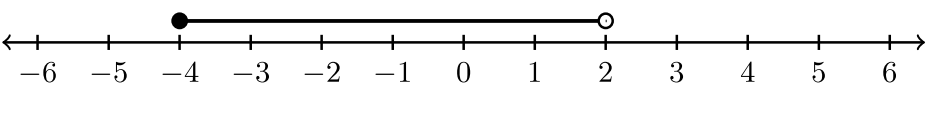$clipboard_e520b9807a5ebbd773c86cc029f9dd4cd.png$
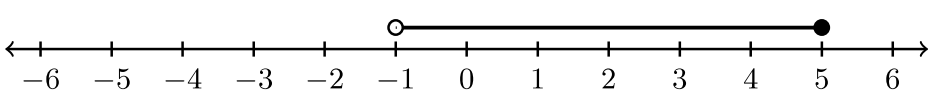$clipboard_e90ef48553dcc2b631e06459ee8b7d36b.png$
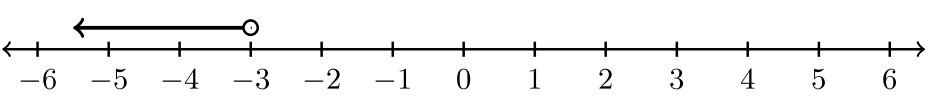$clipboard_e82c969b77994d0dd174ccb04a54f7dec.png$

Для вправ #7 -10 встановіть інтервальні позначення та намалюйте графік, пов'язаний з нерівністю.

Графік			Нерівність	Інтервальні позначення
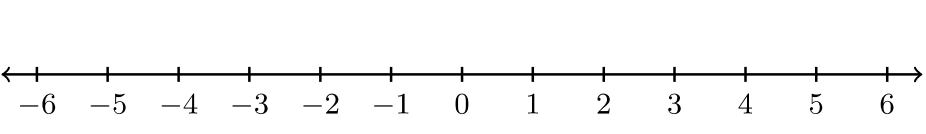$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			$−3 ≤ x ≤ 1$
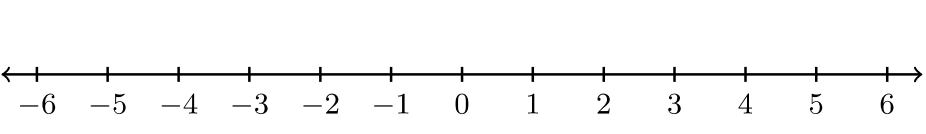$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			$x < 4$
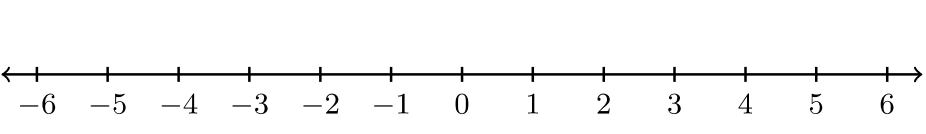$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			$x ≥ −2$
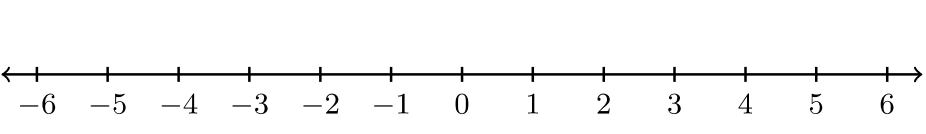$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			$0 ≤ x < 3$

Для вправ #11 -17 намалюйте графік, пов'язаний із заданим інтервальним позначенням.

Графік			Інтервальні позначення
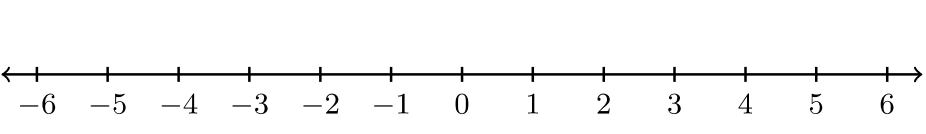$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			$(−∞, 4)$
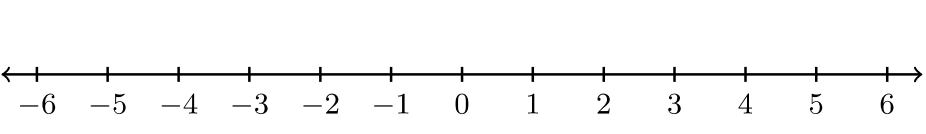$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			$(−∞, −3) ∪ [0, ∞)$
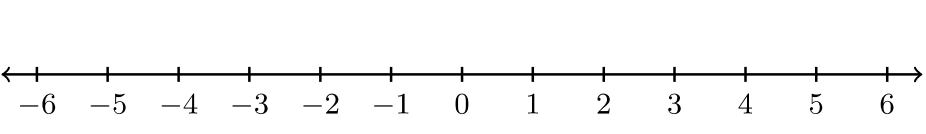$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			$[−1, 1) ∪ [2, ∞)$
$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			$(−∞, −5] ∪ (−1, 5)$
$clipboard_e1fb276fa8366c7f92f1422621f9dcbef.png$			$\left[−\dfrac{\pi}{2} , \dfrac{\pi}{2} \right]$
$clipboard_e1fb276fa8366c7f92f1422621f9dcbef.png$			$(−∞, −\pi] ∪ [\pi, ∞)$
$clipboard_e1fb276fa8366c7f92f1422621f9dcbef.png$			$\left(−\dfrac{3\pi}{2} , −\dfrac{\pi}{2} \right) ∪ \left(-\dfrac{\pi}{2} , 0\right)$

Для #18 -21

а. намалюйте графік складної нерівності.

b. станьте інтервал, використовуючи інтервальне позначення.

$x ≥ 4$ або $x ≤ 0$
$x ≤ – 2\pi$ або $x > \pi$
$−1 > x$ або $2 ≤ x$
$x > 3\pi$ або $x < – \pi$