3.4: Теорема про множник та теорема про залишок

Last updated
Save as PDF

Page ID: 60044

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

В останньому розділі ми обмежилися пошуком перехоплень, або нулів, поліномів, які були враховані просто, або ми звернулися до технології. У цьому розділі ми розглянемо алгебраїчні методи знаходження нулів многочленів на кшталт$h(t)=t^{3} +4t^{2} +t-6$.

Довгий дивізіон

В останньому розділі ми побачили, що ми могли б написати многочлен як добуток факторів, кожен з яких відповідає горизонтальному перехопленню. Якби ми$x = 2$ знали, що це перехоплення многочлена$x^3 + 4x^2 - 5x - 14$, ми могли б здогадатися, що многочлен може бути врахований як$x^{3} +4x^{2} -5x-14=(x-2)$ (щось). Щоб знайти це «щось», ми можемо використовувати поліноміальне ділення.

Приклад$\PageIndex{1}$

Розділити$x^{3} +4x^{2} -5x-14$ на$x-2$.

Рішення

Почніть з написання проблеми у формі довгого поділу

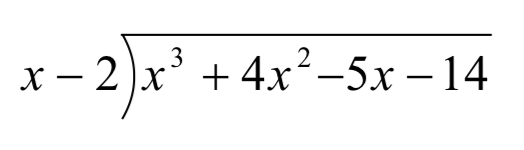
$2019-06-23 5.41.34.png$

Тепер розділимо провідні терміни:$x^{3} \div x=x^{2}$. Найкраще вирівняти його вище того ж терміну в дивідендах. Тепер помножте це$x^{2}$ на$x-2$ і напишіть результат нижче дивідендів.

$2019-06-23 5.42.53.png$

Знову ділимо провідний член залишку на провідний член дільника. $6x^{2} \div x=6x$. Додаємо це до результату, множимо 6 х на$x-2$, і віднімаємо.

$2019-06-23 5.43.34.png$

Це говорить нам,$x^{3} +4x^{2} -5x-14$$x-2$ розділене на є$x^{2} +6x+7$, з залишком нуля. Це також означає, що ми можемо враховувати$x^{3} +4x^{2} -5x-14$ як$\left(x-2\right)\left(x^{2} +6x+7\right)$.

Це дає нам спосіб знайти перехоплення цього многочлена.

Приклад$\PageIndex{2}$

Знайдіть горизонтальні перехоплення$h(x)=x^{3} +4x^{2} -5x-14$.

Рішення

Щоб знайти горизонтальні перехоплення, нам потрібно вирішити$h(x) = 0$. З попереднього прикладу ми знаємо, що функція може бути врахована як$h(x)=\left(x-2\right)\left(x^{2} +6x+7\right)$.

$h(x)=\left(x-2\right)\left(x^{2} +6x+7\right)=0$коли$x = 2$ або коли$x^{2} +6x+7=0$. Це не фактор красиво, але ми могли б використовувати квадратичну формулу, щоб знайти інші два нулі.

\[x=\dfrac{-6\pm \sqrt{6^{2} -4(1)(7)} }{2(1)} =-3\pm \sqrt{2} \nonumber \]

Горизонтальні перехоплення будуть при$(2,0)$$\left(-3-\sqrt{2} ,0\right)$, і$\left(-3+\sqrt{2} ,0\right)$.

Вправа$\PageIndex{1}$

Розділіть$2x^{3} -7x+3$ за$x+3$ допомогою довгого поділу.

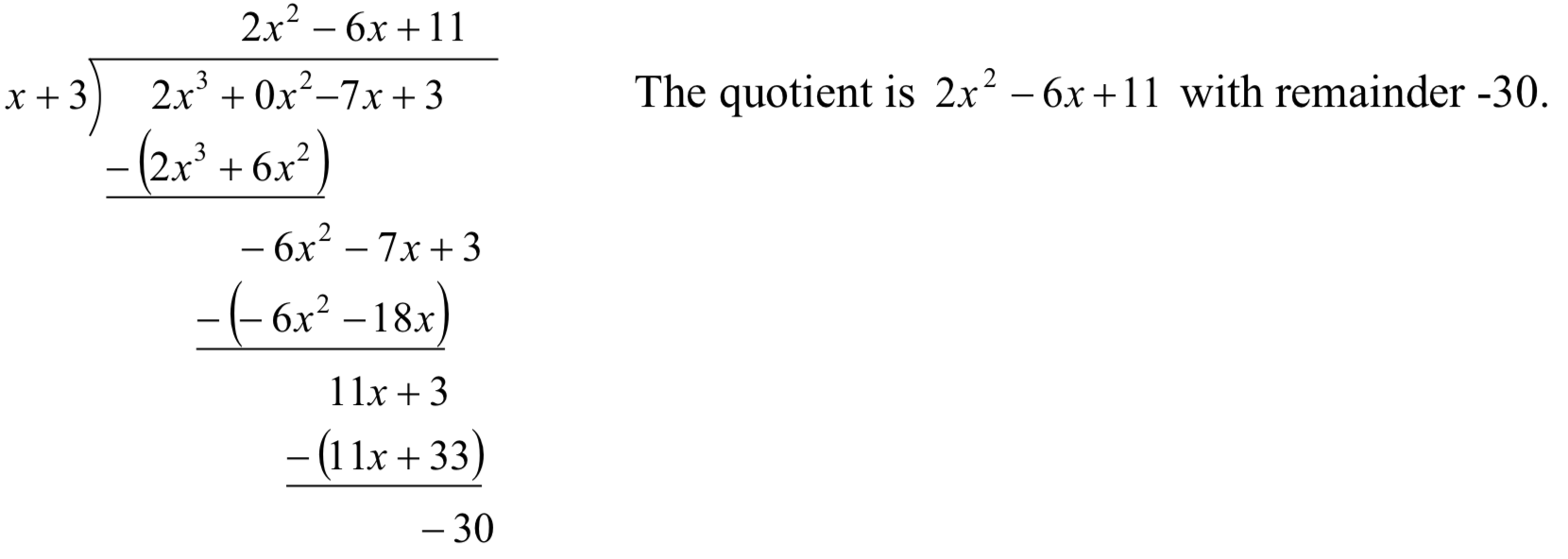
Відповідь: $2019-06-23 6.07.45.png$

Теореми про коефіцієнт і залишок

Коли ми ділимо многочлен,$p(x)$ на якийсь дільник многочлена$d(x)$, ми отримаємо частний многочлен$q(x)$ і, можливо, залишок$r(x)$. Іншими словами,

\[p(x)=d(x)q(x)+r(x)\]

Через ділення залишок буде або дорівнює нулю, або многочлен нижчого ступеня, ніж d (x). Через це, якщо розділити многочлен на член виду$x-c$, то залишок буде дорівнює нулю або константі.

Якщо$p(x)=(x-c)q(x)+r$, то$p(c)=(c-c)q(c)+r=0+r=r$, який встановлює теорему про залишок.

Теорема про залишок

Якщо$p(x)$ многочлен ступеня 1 або більше, а c - дійсне число, то коли p (x) ділиться на$x-c$, залишок дорівнює$p(c)$.

Якщо$x-c$ є множником многочлена$p$, то$p(x)=(x-c)q(x)$ для деякого многочлена$q$. Потім$p(c)=(c-c)q(c)=0$, показ$c$ - це нуль многочлена. Це не повинно нас дивувати - ми вже знали, що якщо поліноміальні фактори виявляють коріння.

Якщо$p(c)=0$, то теорема про залишок говорить нам, що якщо p розділити на$x-c$, то залишок буде дорівнює нулю, а значить$x-c$ - множник$p$.

теорема про множник

Якщо$p(x)$ є ненульовим многочленом, то дійсне число$c$ дорівнює нулю$p(x)$ if і тільки якщо$x-c$ є множником$p(x)$.

Синтетичний поділ

Оскільки ділення на$x-c$ - це спосіб перевірити, чи є число нулем многочлена, було б непогано мати більш швидкий спосіб ділення на,$x-c$ ніж використовувати довгий ділення кожного разу. На щастя, більш швидкі шляхи були виявлені.

Давайте подивимося назад на довгий поділ, який ми зробили в прикладі 1, і спробуємо його впорядкувати. Для початку давайте змінимо всі віднімання на додавання, розподіляючи через негативи.

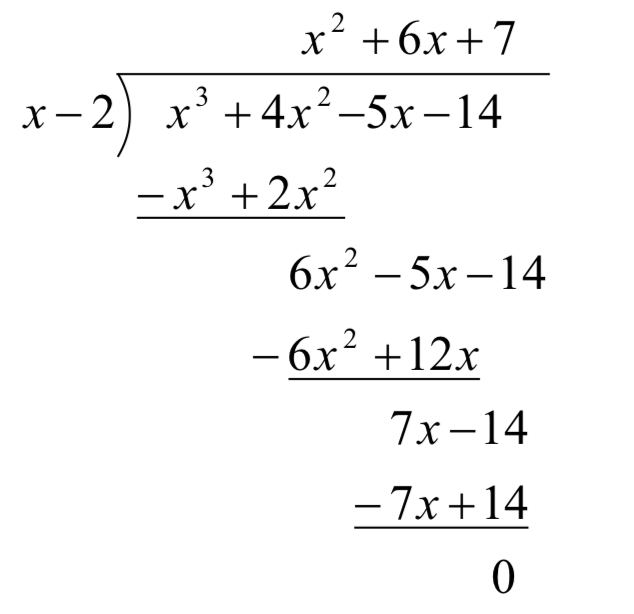
$2019-06-23 5.51.23.png$

Далі, зверніть увагу$-x^{3}$, що терміни$-6x^{2}$, і$-7x$ є повною протилежністю термінам вище них. Алгоритм, який ми використовуємо, гарантує, що це завжди так, тому ми можемо опустити їх, не втрачаючи жодної інформації. Також зауважте, що терміни, які ми «збиваємо» (а саме$\mathrm{-}$ 5x та$\mathrm{-}$ 14), насправді не потрібні для повторного копіювання, тому ми їх також опускаємо.

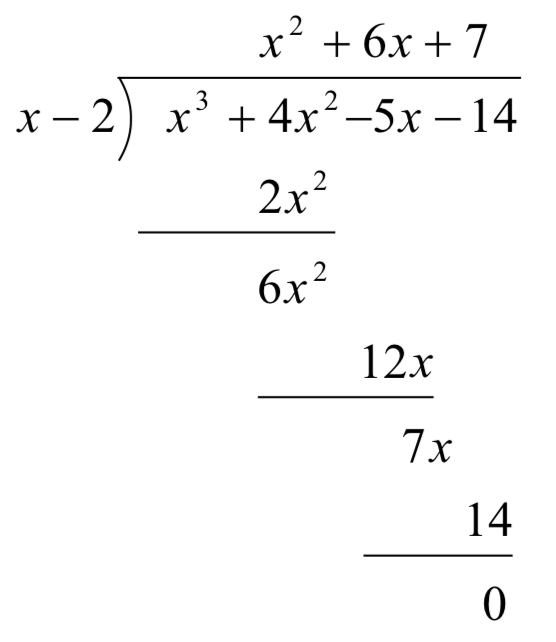
$2019-06-23 5.51.5.png$

Тепер давайте трохи перемістимо речі вгору і, з причин, які стануть зрозумілими через мить, скопіюємо$x^{3}$ їх в останній рядок.

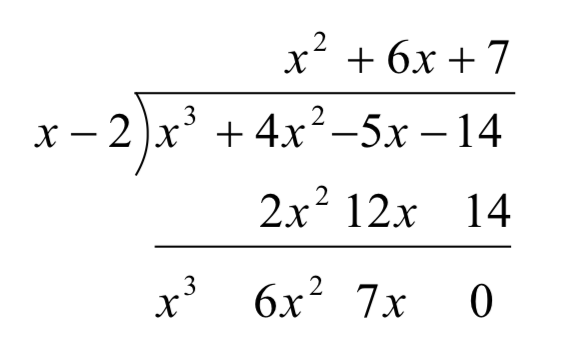
$2019-06-23 5.52.19.png$

Зверніть увагу, що, розташувавши речі таким чином, кожен член в останньому рядку виходить шляхом додавання двох членів над ним. Зауважте також, що частковий многочлен можна отримати, розділивши кожне з перших трьох членів в останньому рядку на$x$ і додаючи результати. Якщо ви витратите час, щоб повернутися до початкової задачі поділу, ви виявите, що саме так ми визначили частний многочлен.

Це означає, що нам більше не потрібно записувати частний многочлен вниз, ні$x$ в дільник, щоб визначити нашу відповідь.

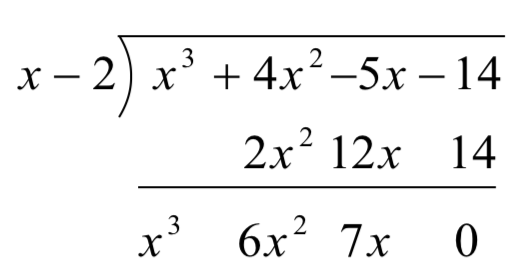
$2019-06-23 5.52.46.png$

Поки що ми впорядкували речі, але ми все ще можемо зробити більше. Давайте візьмемо хвилинку, щоб нагадати собі$2x^{2}$, звідки взялися,$12x$ і 14 у другому ряду. Кожен з цих членів був отриманий множенням долі в частці$x^{2}$, 6x і 7 відповідно на -2 in, потім на -1$x - 2$, коли ми змінили віднімання на додавання. Множення на -2 потім на -1 - це те саме, що і множення на 2, тому замінюємо -2 в дільнику на 2. Крім того, коефіцієнти часткового многочлена збігаються з коефіцієнтами перших трьох членів в останньому рядку, тому ми тепер беремо занурення і запишемо тільки коефіцієнти членів, щоб отримати

Ми побудували синтетичну таблицю поділу для цієї многочленної задачі ділення. Давайте повторно опрацюємо нашу проблему поділу, використовуючи цю таблицю, щоб побачити, як вона значно спрощує процес поділу. Для поділу$x^{3} +4x^{2} -5x-14$ на$x-2$, запишемо 2 на місці дільника і коефіцієнти$x^{3} +4x^{2} -5x-14$ in для дивіденду. Потім «збийте» перший коефіцієнт дивідендів.

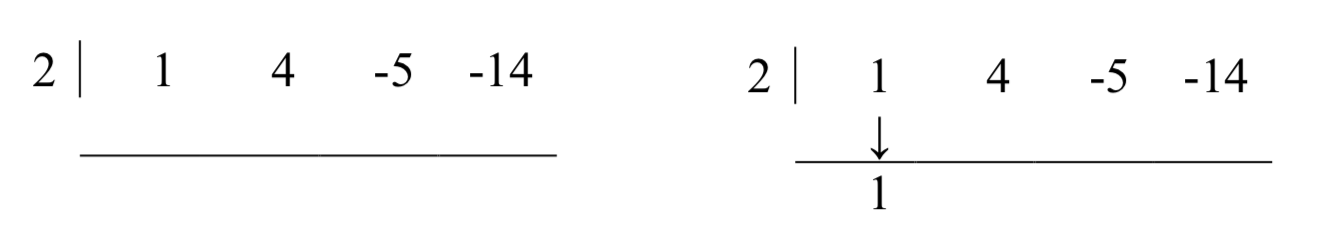
$2019-06-23 5.55.20.png$

Далі візьміть 2 з дільника і помножте на 1, який був «збитий», щоб отримати 2. Напишіть це під 4, потім додайте, щоб отримати 6.

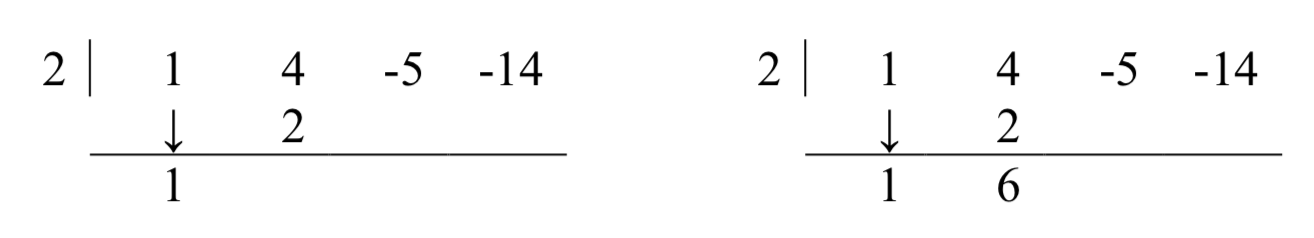
$2019-06-23 5.58.18png$

Тепер візьміть 2 з дільника раз 6, щоб отримати 12, і додати його до -5, щоб отримати 7.

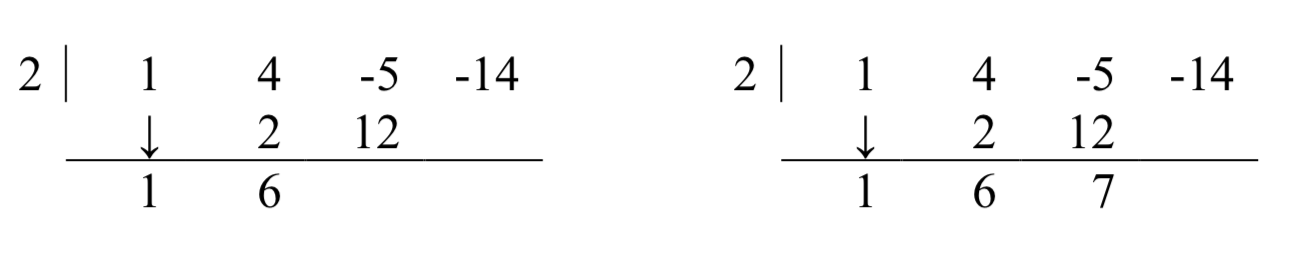
$2019-06-23 5.59.04.png$

Нарешті, візьміть 2 в дільник раз 7, щоб отримати 14, і додати його до -14, щоб отримати 0.

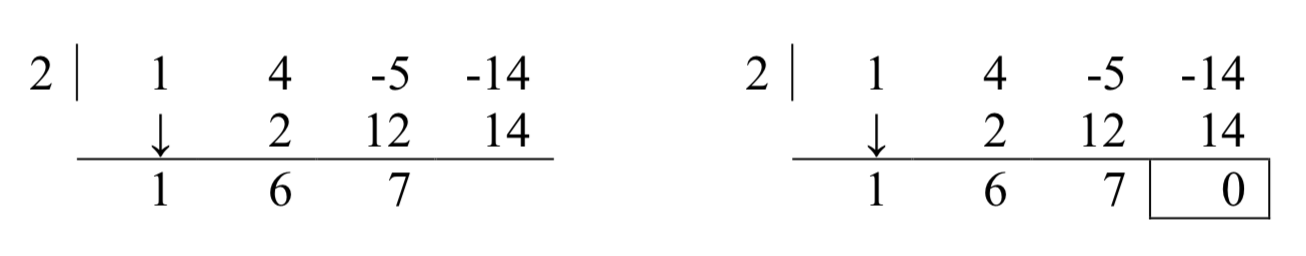
$2019-06-23 5.59.43.png$

Перші три числа в останньому рядку нашої таблиці - це коефіцієнти частного многочлена. Пам'ятайте, ми почали з полінома третього ступеня і розділили на многочлен першого ступеня, тому частка є поліном другого ступеня. Звідси частка є$x^{2} +6x+7$. Число в коробці - це залишок. Синтетичне ділення - наш інструмент вибору для ділення многочленів на дільники виду$x - c$. Важливо відзначити, що він працює тільки для цих видів дільників. Також врахуйте, що коли многочлен (ступеня не менше 1) ділиться на$x - c$, результатом буде многочлен рівно на один менший ступінь. Нарешті, варто витратити час, щоб простежити кожен крок у синтетичному поділі назад до відповідного кроку в довгому поділі.

Приклад$\PageIndex{3}$

Використовуйте синтетичне поділ, щоб розділити$5x^{3} -2x^{2} +1$ на$x-3$.

Рішення

При налаштуванні таблиці синтетичного поділу нам потрібно ввести 0 для коефіцієнта$x$ в дивідендах. Роблячи це дає

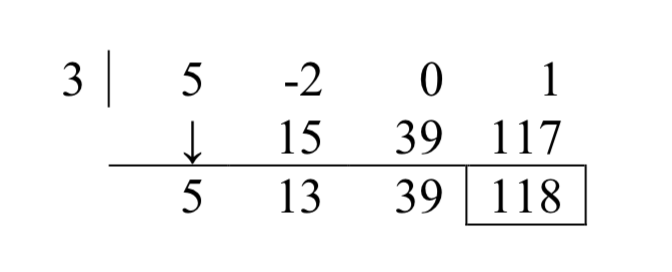
$2019-06-23 6.01.07png$

Оскільки дивіденд був поліном третього ступеня, частка - квадратичний многочлен з коефіцієнтами 5, 13 і 39. Наш коефіцієнт є,$q(x)=5x^{2} +13x+39$ а решта -$r(x) = 118$. Це означає

\[5x^{3} -2x^{2} +1=(x-3)(5x^{2} +13x+39)+118\nonumber \]

Це також означає,$x-3$ що не є фактором$5x^{3} -2x^{2} +1$.

Приклад$\PageIndex{4}$

Розділити$x^{3} +8$ на$x+2$.

Рішення

Для цього поділу переписуємо$x+2$ як$x-\left(-2\right)$ і чинимо як раніше.

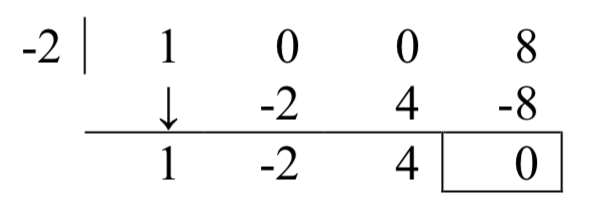
$2019-06-23 6.02.55.png$

Частка дорівнює,$x^{2} -2x+4$ а залишок дорівнює нулю. Так як залишок дорівнює нулю,$x+2$ є коефіцієнтом$x^{3} +8$.

\[x^{3} +8=(x+2)\left(x^{2} -2x+4\right)\nonumber \]

Вправа$\PageIndex{2}$

Розділіть$4x^{4} -8x^{2} -5x$ за$x-3$ допомогою синтетичного поділу.

Відповідь

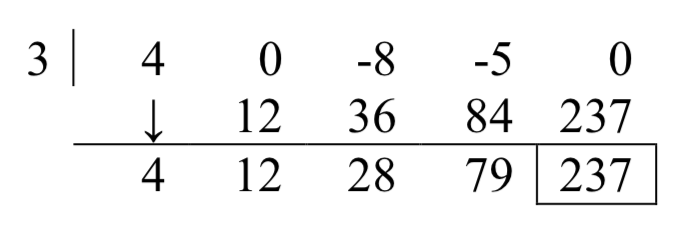
$2019-06-23 6.06.29.png$

$4x^4 - 8x^2 - 5x$ділиться на$x -3$ є$4x^3 + 12x^2 + 28x + 79$ з залишком 237

Використання цього процесу дозволяє знайти дійсні нулі поліномів, припускаючи, що ми можемо з'ясувати хоча б один корінь. Ми розглянемо, як це зробити, у наступному розділі.

Приклад$\PageIndex{5}$

Многочлен$p(x)=4x^{4} -4x^{3} -11x^{2} +12x-3$ має горизонтальний перехоплення$x=\dfrac{1}{2}$ при кратності 2. Знайдіть інші перехоплення$p(x)$.

Рішення

Так як$x=\dfrac{1}{2}$ є перехоплення з кратністю 2, то$x-\dfrac{1}{2}$ є множником двічі. Використовуйте синтетичне поділ, щоб розділити на$x-\dfrac{1}{2}$ два рази.

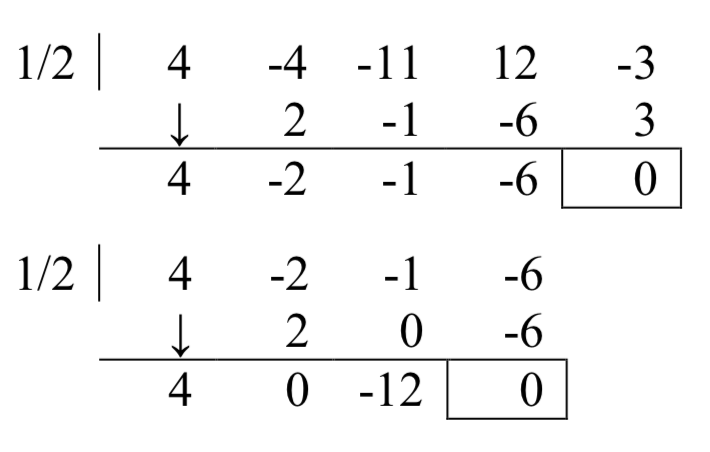
$2019-06-23 6.04.51.png$

З першого дивізіону отримуємо$4x^{4} -4x^{3} -11x^{2} +12x-3=\left(x-\dfrac{1}{2} \right)\left(4x^{3} -2x^{2} -x-6\right)$ Другий дивізіон говорить нам

\[4x^{4} -4x^{3} -11x^{2} +12x-3=\left(x-\dfrac{1}{2} \right)\left(x-\dfrac{1}{2} \right)\left(4x^{2} -12\right)\nonumber \]

Щоб знайти залишилися перехоплення, встановлюємо$4x^{2} -12=0$ і дістаємо$x=\pm \sqrt{3}$.

Зверніть увагу, що це теж означає$4x^{4} -4x^{3} -11x^{2} +12x-3=4\left(x-\dfrac{1}{2} \right)\left(x-\dfrac{1}{2} \right)\left(x-\sqrt{3} \right)\left(x+\sqrt{3} \right)$.

Важливі теми цього розділу

Довге ділення многочленів
Теорема про залишок
Теорема про коефіцієнт
Синтетичний поділ поліномів